Ljetni rok 2015. godine
1. zadatak
Crtež prikazuje dijagrame položaja u ovisnosti o vremenu za tijelo 1 i tijelo 2.
Koja je od navedenih tvrdnja za ta tijela točna?
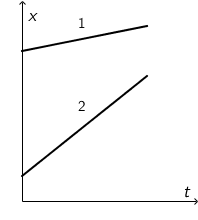
- A. Tijelo 1 ima veću brzinu od tijela 2.
- B. Tijelo 1 ima veću akceleraciju od tijela 2.
- C. Tijelo 2 ima veću brzinu od tijela 1.
- D. Tijelo 2 ima veću akceleraciju od tijela 1.
Kako ovisi nagib pravca u x, t grafu o brzini tijela?
Radi se o jednolikom gibanju. Brzinu iz x, t grafa određujemo kao nagib pravca. Prema tome, veći nagib pravca znači i veću brzinu.
2. zadatak
Satelit X giba se jednoliko po kružnoj putanji oko Zemlje kao što je prikazano na crtežu.
Koja je od navedenih tvrdnja točna za ukupnu silu koja djeluje na satelit X?
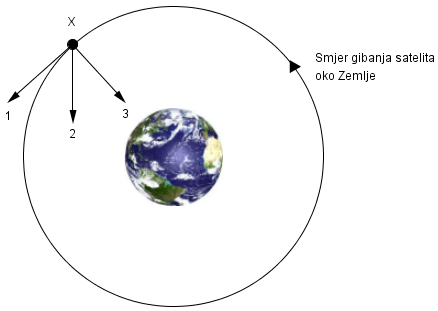
- A. Ukupna sila na satelit X jednaka je nuli.
- B. Ukupna sila na satelit X djeluje u smjeru 1.
- C. Ukupna sila na satelit X djeluje u smjeru 2.
- D. Ukupna sila na satelit X djeluje u smjeru 3.
Koja je sila uzrok gibanja satelita oko Zemlje?
Satelit se giba oko Zemlje zbog djelovanja sile gravitacije. Gravitacijske sila djeluje po pravcu koji prolazi kroz satelit i kroz središte Zemlje.
3. zadatak
Kvadar se giba jednoliko po vodoravnoj podlozi pod djelovanjem vodoravne vučne sile \(\vec{F}\).
Koja je od navedenih tvrdnja točna za silu trenja \(\vec{F_{tr}}\) kojom podloga djeluje na kvadar?
Pretpostavite da su vučna sila i sila trenja jedine sile koje imaju komponentu u vodoravnome smjeru.
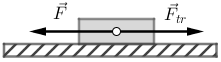
- A. \(\vec{F_{tr}}=\vec{F}\)
- B. \(\vec{F_{tr}}=-\vec{F}\)
- C. \(\vec{F_{tr}}=\vec{F}/2\)
- D. \(\vec{F_{tr}}=-\vec{F}/2\)
Primijenite prvi Newtonov zakon.
Prema prvom Newtonovom zakonu, tijelo će se gibati jednoliko ako je ukupna sila koja na njega djeluje jednaka nuli.

4. zadatak
Tijelo klizi po podlozi bez trenja i elastično se sudari sa zidom. Brzina tijela prije sudara je \(\vec{v_{1}}\), a brzina tijela nakon sudara
\(\vec{v_{2}}\).
Koji crtež prikazuje vektore brzina toga tijela prije i poslije sudara?

- A. crtež A
- B. crtež B
- C. crtež C
- D. crtež D
Kod elastičnog sudara tijelo se odbije jednakom brzinom kojom je pogodilo zid i pod jednakim kutom pod kojim je pogodilo zid.
Kod elastičnog sudara vektor brzine nakon odbijanja ima jednak iznos, a kut upadanja jednak je kutu odbijanja.
5. zadatak
Akceleracija slobodnoga pada na Mjesecu jest g/6, gdje je g akceleracija slobodnoga pada na
Zemlji. Astronaut koji se nalazi na površini Mjeseca o dinamometar ovjesi tijelo mase 1,2 kg.
Koliku silu pokazuje dinamometar?
- A. 0 N
- B. 2 N
- C. 6 N
- D. 12 N
Dinamometar pokazuje težinu tijela koje je na njega ovješeno.
Težina tijela na Mjesecu jednaka je: \[G_{m}=m\cdot g_{m}=m\cdot \frac{g}{6}=1,2\cdot \frac{10}{6}=2\, \textrm{N}\]
6. zadatak
Pri kojoj se promjeni stanja plina ne mijenja volumen plina?
- A. pri izotermnoj promjeni
- B. pri izobarnoj promjeni
- C. pri izohornoj promjeni
- D. pri adijabatskoj promjeni
Pomoć potražite na stranici Izohorna promjena stanja plina
Promjenu stanja plina pri kojoj se volumen ne mijenja nazivamo izohornom promjenom stanja.
7. zadatak
Crtež prikazuje dijagram volumena idealnoga plina u ovisnosti o njegovoj temperaturi izraženoj u kelvinima
(V, t graf).
Tlak plina u stanju A iznosi p.
Koliki je tlak plina u stanju B?
- A. 0.5 p
- B. p
- C. 2 p
- D. 4 p
Pomoć potražite na stranici Izobarna promjena stanja plina..
Iz grafa zaključujemo da se radi o izobarnoj promjeni stanja plina, pa je tlak konstantan za bilo koje stanje na jednoj izobari. Točke A i B nalaze se na jednoj izobari, pa im odgovara stanje jednakog tlaka.
8. zadatak
Uranjanjem u vodu uteg se zagrijao za 4 K, a voda ohladila za 2 K. Mase utega i vode
su jednake. Zanemarite izmjenu topline s okolinom.
Koja je od navedenih tvrdnja točna?
- A. Uteg je primio više topline nego što je voda predala.
- B. Specifični toplinski kapacitet utega veći je nego specifični toplinski kapacitet vode.
- C. Uteg je primio više unutarnje energije nego što je voda predala.
- D. Specifični toplinski kapacitet utega manji je nego specifični toplinski kapacitet vode.
Pomoć potražite na stranici Količina topline.
Toplina koju neko tijelo zagrijavanjem prima ili hlađenjem predaje može se prikazati kao: \[Q=mc\Delta T=mc(T_{2}-T_{1})\] Uteg je primio toplinu \(Q_{1}=mc_{u}\Delta T=mc_{u}\cdot 4\), a voda je predala toplinu \(Q_{2}=mc_{v}\Delta T=mc_{v}\cdot 2\)
Ako te dvije topline izjednačimo, \(Q_{1}=Q_{2}\), dobijemo: \[mc_{u}\cdot 4=mc_{v}\cdot 2\, \Rightarrow c_{u}=c_{v}/2\]
9. zadatak
Dvije jednake neutralne metalne kugle na stalcima od izolatora postavljene su tako da se dodiruju. Negativno nabijeni štap postavljen je pored kugle 1 kao što je prikazano na crtežu. Koja je od navedenih tvrdnja točna?
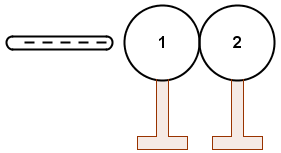
- A. Kugla 1 je pozitivno nabijena, a kugla 2 je negativno nabijena.
- B. Kugla 1 je negativno nabijena, a kugla 2 je pozitivno nabijena.
- C. Kugla 1 je pozitivno nabijena i kugla 2 je pozitivno nabijena.
- D. Kugla 1 je negativno nabijena i kugla 2 je negativno nabijena.
Što se događa s elektronima ako prvoj kugli primaknemo negativno nabijeni štap? Uzmite u obzir da se kugle dodiruju.
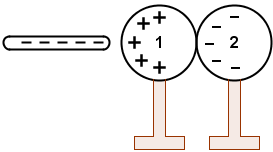
Negativno nabijeni štap odbija elektrone u prvoj kugli na suprotan kraj. Budući da se kugle dodiruju, elektroni prelaze na drugu kuglu. Zbog toga u drugoj kugli ima više, a u prvoj manje elektrona nego kad su bile neutralne. Zato je prva kugla nabijena pozitivno, a druga negativno.
10. zadatak
Dva tijela naboja Q i -Q međusobno se elektrostatski privlače silom iznosa
6 N. Naboj na jednome tijelu smanji se na Q/2, a međusobna
udaljenost tijela ostane ista.
Koji crtež točno prikazuje elektrostatske sile kojima ta tijela međusobno djeluju?
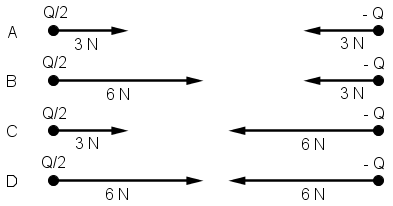
- A. crtež A
- B. crtež B
- C. crtež C
- D. crtež D
Primijenite Coulombov zakon: \[F=k\frac{Q_{1}Q_{2}}{r^{2}}\] Više o električnoj sili između dva točkasta naboja možete saznati na poveznici Električna sila.
Iz Coulombovog zakona: \[F=k\frac{Q_{1}Q_{2}}{r^{2}}\] vidimo da je sila proporcionalna električnom naboju: ako jedan naboj smanjimo dva puta, a drugi ostane nepromijenjen, sila će se dva puta smanjiti.
11. zadatak
Trošilo je spojeno na akumulator i kroz njega prolazi struja 2,5 A tijekom 2 sata.
Pritom se prenese 108 kJ električne energije.
Koliki je napon na krajevima akumulatora?
- A. 6 V
- B. 12 V
- C. 18 V
- D. 24 V
Rad, odnosno energiju električne struje možemo prikazati kao: \[W=UIt\]
Iz prenesene električne energije: \[W=UIt\] za napon dobijemo: \[U=\frac{W}{It}=6\,\textrm{V}\]
12. zadatak
Pored vodljivoga prstena nalazi se ravni vodič kao što je prikazano na crtežu. Ravni vodič i vodljivi prsten miruju.
U kojemu od navedenih slučajeva struja prolazi vodljivim prstenom?

- A. Ravnim vodičem ne prolazi struja i negativno je nabijen.
- B. Ravnim vodičem ne prolazi struja i pozitivno je nabijen.
- C. Ravnim vodičem prolazi izmjenična struja.
- D. Ravnim vodičem prolazi struja stalnoga iznosa.
Prema Faradayovom zakonu elektromagnetske indukcije, u vodiču, koji se nalazi u promjenjivom magnetskom polju, inducira se elektromotorni napon: \[U=-\frac{\Delta \phi }{\Delta t}\]
Ako kroz ravni vodič prolazi izmjenična struja, ona stvara promjenjivo magnetsko polje, pa će se u kružnom vodiču inducirati elektromotorni napon.
13. zadatak
Tijelo mase 2 kg, ovješeno o oprugu konstante elastičnosti 200 N/m, titra vertikalno.
Amplituda titranja je 2 cm.
Kako glasi izraz za elongaciju toga tijela u ovisnosti o vremenu?
- A. \(y=2\;\textrm{m}\;sin(100\;\textrm{s}^{-1}\;t)\)
- B. \(y=2\;\textrm{m}\;sin(10\;\textrm{s}^{-1}\;t)\)
- C. \(y=2\;\textrm{cm}\;sin(100\;\textrm{s}^{-1}\;t)\)
- D. \(y=2\;\textrm{cm}\;sin(10\;\textrm{s}^{-1}\;t)\)
Jednadžbu elongacije kod harmonijskog titranja možemo prikazati kao: \[y=y_{0}\,\textrm{sin}\,\omega t\] ili kao: \[y=y_{0}\,\textrm{cos}\,\omega t\]
- \(y_{0}\) - amplituda titranja
- \(\omega=2\pi/T\) - kružna frekvencija
- \(T\) - period titranja
Kružnu frekvenciju možemo odrediti iz poznate konstante elastičnosti i mase tijela: \(\omega =\sqrt{k/m}\)
Amplituda titranja je zadana, \(y_{0}=2\;\textrm{cm}\), a kružnu frekvenciju izračunamo: \(\omega =\sqrt{k/m}=\sqrt{200/2}=10\, \textrm{s}^{-1}\), pa je točan odgovor D.
14. zadatak
Koja je od navedenih tvrdnja točna za matematičko njihalo u titranju u trenutku kada je iznos akceleracije tijela najveći?
- A. Ukupna je energija tijela najmanja.
- B. Ukupna je sila na tijelo najmanja.
- C. Tijelo je u ravnotežnome položaju.
- D. Otklon je tijela najveći.
Titranje matematičkog njihala malim amplitudama je harmonijsko titranje. Tijelo će harmonijski titrati ako na njega djeluje harmonijska sila: \[F=-kx\] Prema drugom Newtonovom zakonu, akceleraciju tijela možemo odrediti kao: \[a=F/m\] Saznajte više o titranju matematičkog njihala.
Tijelo će harmonijski titrati ako na njega djeluje harmonijska sila: \[F=-kx\] Prema drugom Newtonovom zakonu, akceleraciju tijela možemo odrediti kao: \[a=F/m=-kx/m=-(k/m)\cdot x\] Vidimo da je akceleracija maksimalna ako je i elongacija maksimalna, tj. kada se tijelo nalazi u krajnjem položaju.
15. zadatak
Na crtežu je prikazana slika vala na niti u određenome trenutku. Koja je od navedenih tvrdnja točna za česticu niti označenu slovom Č?
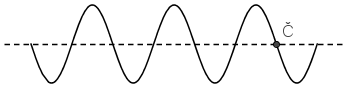
- A. Elongacija je najveća, a brzina je jednaka 0.
- B. Elongacija je najveća i brzina je najveća.
- C. Elongacija je jednaka 0 i brzina je jednaka 0.
- D. Elongacija je jednaka 0, a brzina je najveća.
Ako se elongacija kod harmonijskog titranja mijenja kao: \[y=y_{0}\,\textrm{sin}\,\omega\, t\] onda se brzina mijenja kao: \[v=v_{0}\,\textrm{cos}\,\omega\, t\] Više o nastanku vala na užetu potražite na poveznici Nastanak transverzalnog vala.
Iz crteža možemo zaključiti da je elongacija čestice jednaka 0, pa iz jednadžbe: \[y=y_{0}\,\textrm{sin}\,\omega\, t\] zaključujemo da je \(\omega\, t=0\). Ako to uvrstimo u jednadžbu za brzinu, dobijemo: \[v=v_{0}\,\textrm{cos}\,\omega\, t=v_{0}\,\textrm{cos}\,0=v_{0}\] Prema tome, ako je elongacija nula, brzina je po iznosu najveća (ravnotežni položaj).
16. zadatak
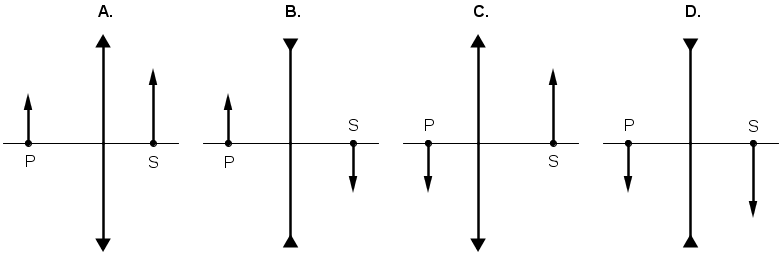
Od predmeta P s pomoću tanke leće dobije se slika S.
Koji od navedenih crteža točno prikazuje položaje predmeta, leće i slike?
Napomena: Pod A. i C. leća je konvergentna, a pod B. i D. divergentna.)
- A. Crtež A.
- B. Crtež B.
- C. Crtež C.
- D. Crtež D.
U sva četiri slučaja slike su realne. Da biste točno odgovorili, odgovorite na ova pitanja:
- Kakvu sliku uvijek daje divergentna leća?
- Kakva je slika u odnosu na predmet koju daje konvergentna leća?
U sva četiri ponuđena slučaja slika i predmet nalaze se na suprotnim stranama leće, tj. slika je realna.
Budući da divergentna leća uvijek daje virtualnu sliku, odgovori B. i D. nisu točni.
Ako konvergentna leća daje realnu sliku, onda su predmet i slika međusobno obrnuti, pa otpada i slučaj A.
17. zadatak
Elektron koji se giba brzinom \(v\) ima de Broglievu valnu duljinu \(\lambda\).
Kolika je de Broglieva valna duljina elektrona koji se giba brzinom \(v/4\)?
- A. \(\lambda/4\)
- B. \(\lambda/2\)
- C. \(2\lambda\)
- D. \(4\lambda\)
Čestica mase \(m\) koja se giba brzinom \(v\) ima de Broglievu valnu duljinu: \[\lambda =\frac{h}{mv}\] \(h\) - Planckova konstanta.
Iz izraza za de Broglievu valnu duljinu: \[\lambda =\frac{h}{mv}\] vidimo da je de Broglieva valna duljina obrnuto razmjerna brzini čestice, pa prema tome ako se čestica giba četiri puta manjom brzinom, imat će četiri puta veću valnu duljinu.
18. zadatak
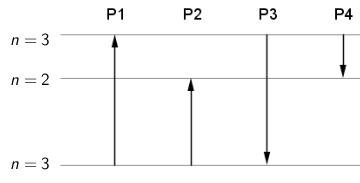
Na crtežu su prikazana tri energetska nivoa nekoga atoma. Strelicama su označeni prijelazi između energetskih nivoa.
Koji od tih prijelaza odgovara apsorpciji fotona najmanje energije?
- A. P1
- B. P2
- C. P3
- D. P4
Proces u kojemu atom prelazi iz nižeg u više energetsko stanje nazivamo apsorpcijom energije, odnosno fotona. Energija koju je atom apsorbirao
jednaka je razlici konačne i početne energije.
Proces u kojemu atom prelazi iz višeg u niže energetsko stanje nazivamo emisijom fotona. Energija fotona kojega je atom emitirao jednaka je razlici
početne i konačne energije.
Procesi P1 i P2 odgovaraju apsorpciji fotona, a P3 i P4 emisiji fotona. Iz crteža vidimo da je atom apsorbirao manje energije u procesu P2 nego u P1.
19. zadatak
Svjetlost određenoga intenziteta pada na metal čiji je izlazni rad 2 eV. Izbijeni elektroni imaju maksimalnu kinetičku
energiju 1 eV. Intenzitet svjetlosti poveća se dva puta.
Kolika će biti maksimalna kinetička energija izbijenih elektrona?
- A. 0,5 eV
- B. 1 eV
- C. 2 eV
- D. 3 eV
O čemu ovisi brzina izbačenih elektrona pa prema tome i njihova kinetička energija?
O intenzitetu ili frekvenciji upadne svjetlosti?
Kinetička energija fotoelektrona (elektroni izbačeni iz metala zbog djelovanja svjetlosti) ne ovisi o intenzitetu svjetlosti. O intenzitetu svjetlosti ovisi samo broj izbačenih elektrona.
20. zadatak
U koji izotop prelazi \(_{\,\,92}^{236}\textrm{U}\) alfa raspadom?
- A. \(_{\,\,90}^{232}\textrm{Th}\)
- B. \(_{\,\,90}^{234}\textrm{Th}\)
- C. \(_{\,\,94}^{238}\textrm{Pu}\)
- D. \(_{\,\,94}^{240}\textrm{Pu}\)
Pomoć potražite na stranici Alfa-radioaktivnost.
Jednadžbu alfa-raspada zapisujemo na osnovu zakona očuvanja broja protona i broja nukleona: \[_{\,\,92}^{236}\textrm{U}\rightarrow _{2}^{4}\textrm{He} + _{\,\,90}^{232}\textrm{Th}\]
21. zadatak
Koliko je vrijeme poluraspada nekoga elementa ako se nakon 40 dana raspadne 75 % početnoga broja atoma?
- A. 10 dana
- B. 20 dana
- C. 40 dana
- D. 80 dana
Više o zakonu radioaktivnog raspada možete saznati na poveznici Zakon radioaktivnog raspada
Zadatak možemo riješiti i pomoću zakona radioaktivnog raspada: \[N=N_{0}\cdot 2^{-t/T}\] Ako uzmemo da je broj jezgri koje se nisu raspale za 40 dana jednak \(N=0.25\,N_{0}\), dobijemo jednadžbu: \[0.25N_{0}=N_{0}\cdot 2^{-t/T}\] Jednadžbu možemo pojednostaviti: \[2^{-t/T}=2^{-2}\] Sada dobijemo: \[-\frac{t}{T}=-2\] Konačno: \[T=\frac{t}{2}=20 \, \textrm{dana}\]
22. zadatak
Tijela X i Y u početku miruju na istoj visini iznad horizontalne podloge. U nekome trenutku tijelo X izbačeno je horizontalno brzinom
v, a tijelo Y istodobno ispušteno.
Koja je od navedenih tvrdnja točna ako se zanemari otpor zraka?
- A. Na tlo će prvo pasti tijelo X.
- B. Na tlo će prvo pasti tijelo Y.
- C. Tijela će na tlo pasti istodobno.
Više o složenom gibanju i hicima možete saznati na poveznici Složena gibanja - hici. Podignite tijelo na neku visinu, vektor brzine postavite horizontalno i pokrenite animaciju. Zabilježite koliko je vremena tijelo padalo. Vratite animaciju na početak i pomoću klizača postavite brzinu na nulu (slobodni pad). Pokrenite annimaciju i zabilježite potrbno vrijeme. Što zaključujete?
Radi se o složenom gibanju koje se sastoji od jednolikog gibanja po horizontalnom pravcu i slobodnog pada. Za složena gibanja vrijedi
princip (načelo) neovisnosti gibanja:
Složeno gibanje može se rastaviti na jednostavna gibanja koja ne utječu jedno na drugo i događaju se istodobno. Svako od tih jednostavnih
gibanja traje jednako dugo kao i složeno gibanje.
Prema tome, tijela će na tlo pasti istodobno.
23. zadatak
Na izvor stalnoga napona priključeno je trošilo.
Što će se dogoditi sa strujom kroz trošilo ako se smanji otpor toga trošila?
- A. Smanjit će se.
- B. Ostat će ista.
- C. Povećat će se.
Primijenite Ohmov zakon za dio strujnog kruga.
Iz Ohmovog zakona: \[I =\frac{U}{R}\] vidimo da je struja obrnuto razmjerna s otporom. Prema tome, ako se otpor trošila smanji, struja će se povećati.
24. zadatak
Snop monokromatske svjetlosti pada okomito na dvije pukotine. Na zastoru nastaje interferentna slika.
Što treba učiniti da se smanji razmak između svijetlih pruga na zastoru?
- A. Povećati razmak između pukotina
- B. Povećati udaljenost između pukotina i zastora
- C. Povećati valnu duljinu svjetlosti
Više o interferenciji dva izvora svjetlosti možete saznati na poveznici Interferencija svjetlosti
Udaljenost između svjetlih pruga interferencije jednaka je: \[s=\frac{\lambda a}{d}\]
- s - udaljenost između susjednih pruga
- \(\lambda\) - valna duljina svjetlosti
- a - udaljenost između izvora i zastora
- d - udaljenost između izvora
25. zadatak
Tijelo je izbačeno s tla vertikalno uvis brzinom 5 m/s.
Do koje će visine iznad tla stići tijelo prije nego što počne padati natrag prema tlu?
Zanemarite sile kojima zrak djeluje na tijelo.
Odgovor:
Budući da otpor zraka ne uzimamo u obzir, sustav je zatvoren pa možemo primijeniti zakon očuvanja mehaničke energije.
Više o zakonu očuvanja energije možete saznati na poveznici
Očuvanje mehaničke energije.
Prema zakonu očuvanja mehaničke energije, ukupna je energija zatvorenog sustava konstantna.
U početnom trenutku, tijelo ima samo kinetičku energiju:
\[E_{1}=\frac{mv^{2}}{2}\]
U najvišoj točki tijelo za trenutak zastane, zbog čega mu je kinetička energija jednaka nuli, pa je ukupna energija jednaka potencijalnoj:
\[E_{2}=mgh\]
Ako te dvije energije izjednačimo, dobijemo:
\[h=\frac{v^{2}}{2g}=1,25\, \textrm{m}\]
26. zadatak
Zrakoplov mase \(1,5\cdot 10^{5}\, \textrm{kg}\) stoji na početku piste za uzlijetanje. Tijekom 25 s jednoliko ubrzava do brzine
65 m/s koja je potrebna za uzlijetanje.
Kolika srednja sila djeluje na zrakoplov za vrijeme gibanja po pisti?
Odgovor:
O kakvom se gibanju radi? Primijenite odgovarajuću formulu koja povezuje akceleraciju i brzinu.
Zrakoplov se giba jednoliko ubrzano. Iz formule: \[v=at\] odredimo akceleraciju: \[a=\frac{v}{t}\] Prema drugom Newtonovom zakonu sila je jednaka: \[F=ma=m\cdot \frac{v}{t}=1,5\cdot 10^{5}\cdot \frac{65}{25}=390000\, \textrm{N}=3,9\cdot 10^{5\,}\textrm{N}\]
27. zadatak
Korisnost nekoga Carnotova stroja jest 25 %. Temperatura toplijega spremnika jest 124 °C.
Kolika je temperatura hladnijega spremnika?
Rezultat zaokružite na cijeli broj.
Odgovor:
Više o korisnosti toplinskog stroja možete saznati na poveznici Carnotov kružni proces.
Korisnost Carnotovog stroja jednaka je: \[\eta =\frac{T_{1}-T_{2}}{T_{1}}\] Za temperaturu hladnijeg spremnika dobijemo: \[T_{2}={T}_{1}(1-\eta )=298\,\textrm{K}={25}\,^{0}\textrm{C}\]
28. zadatak
Snop elektrona prolazi između dviju elektroda. S jedne na drugu elektrodu tijekom 2 s prijeđe \(10^{11}\) elektrona.
Kolika struja prolazi između elektroda?
Rezultat prikažite u znanstvenom zapisu.
Odgovor:
Struju definiramo kao: \[I=\frac{\Delta Q} {\Delta t}\]
Električna struja jednaka je električnom naboju koji u jedinici vremena prođe poprečnim presjekom vodiča: \[I=\frac{\Delta Q} {\Delta t}\] Električni naboj možemo prikazati kao: \[\Delta Q=N\cdot e\] Struja koja prolazi između elektroda jednaka je: \[I=\frac{\Delta Q} {\Delta t}=\frac {N\cdot e}{\Delta t}=8\cdot 10^{-9}\:\textrm{A}\]
29. zadatak
Svjetlost valne duljine 500 nm pada na optičku rešetku. Maksimum trećega reda vidi se pod kutom 30°.
Kolika je konstanta te rešetke?
Odgovor:
Ako na optičku rešetku pada svjetlost, dolazi do difrakcije.
Zadatak možete lako riješiti na osnovu crteža:
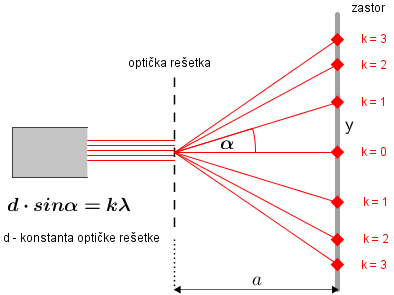
Za optičku rešetku vrijedi: \[d\cdot \textrm{sin}\,\alpha =k\lambda\] Za konstantu optičke rešetke dobijemo: \[d=\frac{k\lambda }{\textrm{sin} \, \alpha }=\frac{3\cdot 5\cdot 10^{-7}}{0,5}=3\cdot 10^{-6}\, \textrm{m}\]
30. zadatak
Mioni u laboratorijskome sustavu gibaju se brzinom 0,9 c i imaju vrijeme poluraspada
\(1,44\cdot 10^{-5}\, \textrm{s}\).
Koliko je vrijeme poluraspada miona u sustavu u kojemu miruju?
Rezultat prikažite u znanstvenom zapisu s dva decimalna mjesta.
Odgovor:
Pomoć potražite na poveznici Dilatacija vremena.
Vrijeme u sustavu u kojemu mioni miruju (sustav koji se giba brzinom 0,9 c) \(T_{0}\) i vrijeme koje mjere promatrači u laboratorijskom sustavu, \(T\), povezani su relacijom: \[T=\frac{T_{0}}{\sqrt{1-v^{2}/c^{2}}}\] Iz te relacije dobijemo: \[T_{0}=T\sqrt{1-v^{2}/c^{2}}=6,28\cdot 10^{-6}\, \textrm{s}\]
31. zadatak
Uteg mase \(1\,\textrm{kg}\) ovješen je na dinamometar i uronjen u tekućinu gustoće \(1\, \textrm{kg/dm}^{3}\).
Dinamometar pokazuje silu iznosa \(8\,\textrm{N}\).
Koliki je obujam toga utega?
Odgovor: \(\textrm{m}^3\)
Na tijelo uronjeno u tekućinu djeluju sila teža i uzgon. Kako odrediti rezultantnu silu?
Sila teža usmjerena je vertikalno prema dolje, a uzgon vertikalno prema gore.
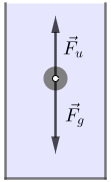
\[F=F_{g}-F_{\textrm{u}}\] Iznosi sile teže, uzgona i rezultantne sile jednaki su: \[ \begin{matrix} \begin{align*} &F_{g}=m\,g\\ &F_{\textrm{u}}=\rho\,g\,V\\ &F=m\,g-\rho\,g\,V\\ \end{align*} \end{matrix} \] Volumen tijela jednak je: \[V=\frac{m\,g-F}{\rho\,g}\] \[V=2\cdot 10^{-4}\,\textrm{m}^{3}\]
32. zadatak
Dva mola jednoatomnog idealnoga plina izohorno se zagrijava od \(273\,K\) do \(400\,K\).
Koliko se pritom promijeni unutarnja energija toga plina?
Rezultat zaokružite na cijeli broj.
Odgovor:
Kod izohornog zagrijavanja plin ne obavlja rad, nego se toplina koju primi pretvara u unutarnju energiju. Unutarnja energija jednoatomnog idealnog plina jednaka je: \[U=\frac{3}{2}N\,k\,T\] \(N\) je broj molekula, a \(k=1,38\cdot 10^{-23}\,\textrm{J}/\textrm{K}\) Boltzmannova konstanta.
Pomoću izraza za unutarnju energiju idealnog plina: \[U=\frac{3}{2}N\,k\,T\] zaključujemo da je promjena unutarnje energije jednaka: \[\Delta U=\frac{3}{2}N\,k\,\Delta T\] Broj molekula (u ovom primjeru je to broj atoma jer je plin jednoatoman) odredimo pomoću broja molova \(n\) i Avogadrove konstante \(N_\textrm{A}=6,023\cdot 10^{23}\,\textrm{mol}^{-1}\) \[N=n\, N_\textrm{A}\] Promjena unutarnje energije dva mola jednoatomnog idealnog plina jednaka je: \[\Delta U=\frac{3}{2}n\, N_\textrm{A}\,k\,\Delta T\] \[\Delta U=3167\,\textrm{J}\]
33. zadatak
Zavojnica i otpornik otpora \(25\,\Omega\) serijski su spojeni na izvor izmjeničnoga napona \(20\,\textrm{V}\)
frekvencije \(50\,\textrm{Hz}\). Omski otpor zavojnice je \(10\,\Omega\), a njezin induktivitet \(0,1\,\textrm{H}\).
Kolika struja prolazi zavojnicom?
Rezultat zaokružite na cijeli broj.
Odgovor:
Ukupni otpor (impedancija) u krugu izmjenične struje jednak je: \[Z=\sqrt{R^{2}+\left ( R_{L}-R_{C} \right )^2}\]
U krugu stuje nema kondenzatora pa je impedancija jednaka: \[Z=\sqrt{R^{2}+{R_{L}}^{2}}\] Induktivni otpor jednak je: \[R_{L}=L\,\omega=L\cdot 2\,\pi\,f\] Struju odredimo na osnovu Ohmovog zakona za izmjeničnu struju: \[ \begin{matrix} \begin{align*} &I=\frac{U}{Z}\\ &I=\frac{U}{\sqrt{R^{2}+{R_{L}}^{2}}}\\ &I=0,43\,\textrm{A} \end{align*} \end{matrix} \]
34. zadatak
Crtež prikazuje transverzalni val u nekome trenutku koji se širi duž osi \(x\) brzinom \(1,5\,\textrm{m/s}\) kroz neko sredstvo. Udaljenost od točke P do točke Q jest \(0,15\,\textrm{m}\). Udaljenost točke R od osi \(x\) jest \(0,12\,\textrm{m}\).
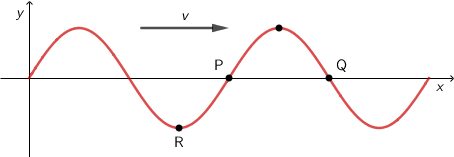
Kolika je maksimalna brzina čestica toga vala?
Rezultat zaokružite na dvije decimale.
Odgovor:
Pri širenju transverzalnog vala čestice sredstva titraju okomito na smjer širenja. Maksimalna brzina čestica sredstva je: \[v_{0}=\frac{2\,A\,\pi}{T}\] \(A\) je amplituda vala, a \(T\) period.
Iz crteža čitamo: \[ \begin{matrix} \begin{align*} &A=0,12\,\textrm{m}\\ &\frac{\lambda}{2}=0,3\,\textrm{m}\Rightarrow \lambda=0,3\,\textrm{m}\\ \end{align*} \end{matrix} \] Period vala odredimo iz izraza za brzinu širenja vala: \[v=\frac{\lambda}{T}\Rightarrow T=\frac{\lambda}{v}=0,2\,\textrm{s}\] Maksimalna brzina titranja čestica sredstva je: \[v_{0}=\frac{2\,A\,\pi}{T}=3,77\,\textrm{m/s}\]
35. zadatak
Kolika je de Broglieva valna duljina elektrona koji se ubrzao kroz napon od
\(200\,\textrm{V}\)?
Elektron je u početnoj točki mirovao.
Rezultat prikažite u znanstvenom zapisu s jednim decimalnim mjestom.
Odgovor: \(\textrm{m}\)
Električno polje pri ubrzavanju elektrona izvrši rad: \[W=e\,U\] koji se pretvara u kinetičku energiju elektrona: \[E_{k}=\frac{1}{2}m\,v^{2}\]
\[ \begin{matrix} \begin{align*} &eU=\frac{1}{2}m\,v^{2}\\ &p=m\,v\\ &eU=\frac{p^{2}}{2\,m}\\ &p=\sqrt{2\,m\,e\,U}\\ &\lambda=\frac{h}{p} \\ &\lambda=\frac{h}{\sqrt{2\,m\,e\,U}}\\ &\lambda=8,7\cdot 10^{-11}\,\textrm{m} \end{align*} \end{matrix} \]