Ljetni rok 2020. godine
1. zadatak
Tijelo se giba jednoliko ubrzano i u četvrtoj sekundi prijeđe put od 10,5 m.
Kolika je akceleracija tijela ako je tijelo na početku mirovalo?
- A. 1,31 m/s2
- B. 2,33 m/s2
- C. 2,63 m/s2
- D. 3 m/s2
Put kod jednoliko ubrzanog pravocrtnog gibnja prikazujemo izrazom: \[s=v_{0}\,t+\frac{a}{2}\,t^{2}\]
2. zadatak
Na kojoj je slici ispravno prikazan dijagram sila na loptu koja se giba jednoliko pravocrtno po ravnoj podlozi bez trenja?
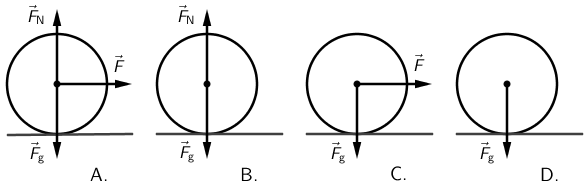
- A. Na slici A.
- B. Na slici B.
- C. Na slici C.
- D. Na slici D.
Primijenite prvi Newtonov zakon.
Tijelo će se gibati jednoliko pravocrtno ako je rezultanta svih sila koje na njega djeluju jednaka nuli (Prvi Newtonov zakon). Točno je prikazan dijagram sila koje djeluju na tijelo na slici B.
3. zadatak
Traktor mase \(m\) ore njivu u obliku kružnice polumjera \(r\) stalnom brzinom \(v\).
Koliko iznosi rad sile podloge na traktor kada traktor jednom obiđe kružnicu?
- A. Nula
- B. \(2\,m\,g\,\pi/r\)
- C. \(2\,r\,m\,g\,\pi\)
- D. \(2\,\pi\, m\,v^{2}\)
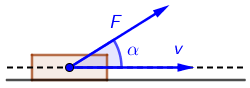
Rad kojega obavi stalna sila \(F\) koja zatvara kut \(\alpha\) sa smjerom gibanja: \[W=F\,s\,\textrm{cos}\,\alpha\] gdje je \(s\) put kojega je tijelo prešlo zbog djelovanja sile.
Sila kojom podloga djeluje na kotače traktora okomita je na smjer gibanja traktora: \[W=F\,s\,\textrm{cos}\,\alpha=F\,s\,\textrm{cos}\,90^{0}=0\]
4. zadatak
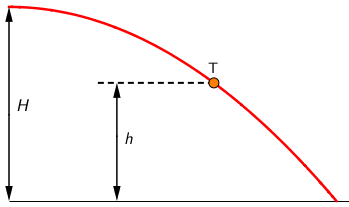
Tijelo je izbačeno s visine H brzinom v0 u horizontalnome smjeru.
Na slici je prikazana putanja tijela te točka T u kojoj se tijelo nalazi na visini h.
Koji od navedenih izraza vrijedi za brzinu tijela v u točki T? Zanemarite otpor zraka.
- A. \(v^{2}=v_{0}^{2}+2\,g\,H\)
- B. \(v^{2}=2\,g\,h\)
- C. \(v^{2}=2\,g\,\left (H-h\right )\)
- D. \(v^{2}=v_{0}^{2}+2\,g\,\left (H-h\right )\)
Horizontalna komponenta brzine cijelo vrijeme gibanja jednaka je početnoj brzini:
\[v_{x}^{\,}=v_{0}^{\,}\]
Vertikalna komponenta brzine mijenja se kao kod jednoliko ubrzanog gibanja:
\[v_{y}^{\,}=\sqrt{2\,g\,s_{y}^{\,}}\]
gdje je \(s_{y}^{\,}\) put kojega tijelo prijeđe u vertikalnom smjeru od točke iz koje je bačeno.
Više o horizontalnom hicu potražite na poveznici
horizontalni hitac.
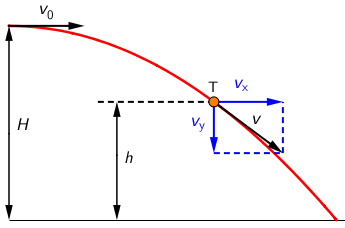
Odredimo horizontalnu i vertikalnu komponentu brzine u točki T: \[v_{x}^{\,}=v_{0}^{\,}\Rightarrow v_{x}^{2}=v_{0}^{2}\] \[v_{y}^{2}=2\,g\,s_{y}^{\,}=2\,g\,\left (H-h \right )\] Primijenimo Pitagorin poučak: \[v^{2}=v_{x}^{2}+v_{y}^{2}\] \[v^{2}=v_{0}^{2}+2\,g\,\left (H-h \right )\]
5. zadatak
Koliko iznosi akceleracija slobodnoga pada na površini Marsa \(g_{\small{\textrm{M}}}\) u usporedbi s akceleracijom slobodnoga pada na površini Zemlje \(g_{\small{\textrm{Z}}}\) ako je masa Marsa \(m_{\small{\textrm{M}}}=0,107\,m_{\small{\textrm{Z}}}\) i polumjer Marsa \(R_{\small{\textrm{M}}}=0,53\,R_{\small{\textrm{Z}}}\)?
- A. \(g_{\small{\textrm{M}}}=0,20\,g_{\small{\textrm{Z}}}\)
- B. \(g_{\small{\textrm{M}}}=0,38\,g_{\small{\textrm{Z}}}\)
- C. \(g_{\small{\textrm{M}}}=0,63\,g_{\small{\textrm{Z}}}\)
- D. \(g_{\small{\textrm{M}}}=4,95\,g_{\small{\textrm{Z}}}\)
Pomoć potražite na poveznici Opći zakon gravitacije.
Akceleracija slobodnog pada na površini nekog planeta je: \[g=G\,\frac{M}{R^{2}}\]
- \(M\) - masa planeta
- \(R\) - polumjer planeta
6. zadatak
U zatvorenoj posudi nalazi se idealni plin na temperaturi \(75\,^0\textrm{C}\) i tlaku \(p_{1}^{\,}\).
Što vrijedi za tlak \(p_{2}^{\,}\) u posudi nakon izohornoga zagrijavanja plina do temperature \(150\,^0\textrm{C}\)?
- A. \( p_{2}^{\,}=\large\frac{p_{1}^{\,}}{2}\)
- B. \( p_{2}^{\,}=p_{1}^{\,}\)
- C. \( p_{1}^{\,} < p_{2}^{\,} < 2\,p_{1}^{\,}\)
- D. \( p_{2}^{\,}=2\,p_{1}^{\,}\)
Izohornu promjenu stanja plina (promjena stanja plina pri kojoj je volumen plina konstantan), opisujemo jednadžbom: \[\frac{p}{T}=\textrm{konst.}\] Omjer tlaka i termodinamičke temperature je konstantan pa ovu jednadžbu zapisujemo i kao: \[\frac{p_{1}^{\,}}{T_{1}}=\frac{p_{2}^{\,}}{T_{2}}\]
Izohorna promjena stanja plina: \[\frac{p_{1}^{\,}}{T_{1}}=\frac{p_{2}^{\,}}{T_{2}}\] \[p_{2}^{\,}=\frac{T_{2}}{T_{1}}\,p_{1}^{\,}\] \[p_{2}^{\,}=\frac{150+273,15}{75+273,15}\,p_{1}^{\,}=1,215\,p_{1}^{\,}\]
7. zadatak
U posudi na temperaturi \(T\) nalazi se smjesa dvaju idealnih plinova \(\textrm{O}_{2}\) i \(\textrm{H}_{2}\). Masa molekule \(\textrm{O}_{2}\)
šesnaest je puta veća od mase molekule \(\textrm{H}_{2}:m\,\left (\textrm{O}_{2}\right )=16\,m\left (\textrm{H}_{2}\right )\).
Koliki je omjer srednjih kinetičkih energija molekule kisika i vodika
\(E_{\textrm{k}}\left (\textrm{O}_{2}\right )/E_{\textrm{k}}\left (\textrm{H}_{2}\right )\)?
- A. 1/16
- B. 1
- C. 4
- D. 16
Srednja kinetička energija molekula jednoatomnog idealnog plina je: \[\overline{E}_\textrm{k}=\frac{3}{2}k\,T\] Srednja kinetička energija molekula dvoatomnog idealnog plina je: \[\overline{E}_\textrm{k}=\frac{5}{2}k\,T\]
Srednja kinetička energija molekula dvoatomnog idealnog plina je: \[\overline{E}_\textrm{k}=\frac{5}{2}k\,T\] Srednja kinetička energija molekula idealnog plina ovisi o temperaturi plina i o broju atoma ugrađenih u molekulu. Molekule kisika i vodika su dvoatomne i nalaze se u posudi na istoj temperaturi. Zato će srednja kinetička energija molekula kisika biti jednaka srednjoj kinetičkoj energiji molekula vodika: \[\overline{E}_{\textrm{k}}\left (\textrm{O}_{2}\right )=\overline{E}_{\textrm{k}}\left (\textrm{H}_{2}\right )\]
8. zadatak
Koja je od navedenih termodinamičkih veličina jednaka nuli u kružnome procesu?
- A. \(\Delta U\)
- B. \(Q\)
- C. \(W\)
- D. \(E_{\textrm{k}}\)
Pomoć potražite na poveznici Prvi zakon termodinamike.
Napomena
Neprecizno formuliran zadatak.
U kružnom procesu unutarnja energija se mijenja (povećava ili smanjuje), ali na kraju kružnog procesa promjena unutarnje energije
jednaka je nuli:
\[\Delta U=0\]
9. zadatak
Otpornik otpora \(R=100\,\Omega\) spojen je na izvor izmjeničnoga napona. Na slici je prikazana ovisnost napona na otporniku o vremenu.
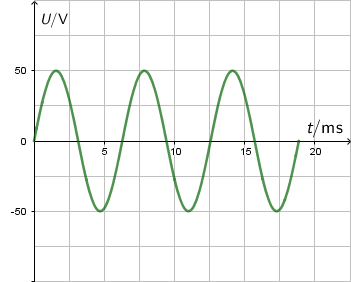
Koliko iznosi maksimalna električna struja koja prolazi kroz otpornik?
- A. 0 A
- B. 0,5 A
- C. 50 A
- D. 5000 A
Ohmov zakon: \[I=\frac{U}{R}\] Za stalni otpor struja će biti maksimalna ako je napon maksimalan.
Iz grafa očitamo maksimalni napon: \[U_{0}=50\,\textrm{V}\] Primijenimo Ohmov zakon: \[I_{0}=\frac{U_{0}}{R}\] \[I_{0}=0,5\,\textrm{A}\]
10. zadatak
Na spojnici dvaju točkastih naboja \(Q_{1}\) i \(Q_{2}\) smješten je u točki T treći naboj \(q\) kao što je prikazano na slici.
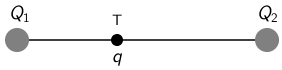
Kakvi su po predznaku i iznosu naboji \(Q_1\) i \(Q_2\) ako je ukupna sila na naboj \(q\) jednaka nuli?
- A. Naboji \(Q_1\) i \(Q_2\) imaju suprotne predznake i \(Q_1\) je veći po iznosu od \(Q_2\).
- B. Naboji \(Q_1\) i \(Q_2\) imaju suprotne predznake i \(Q_2\) je veći po iznosu od \(Q_1\).
- C. Naboji \(Q_1\) i \(Q_2\) imaju iste predznake i \(Q_1\) je veći po iznosu od \(Q_2\).
- D. Naboji \(Q_1\) i \(Q_2\) imaju iste predznake i \(Q_2\) je veći po iznosu od \(Q_1\).
Na naboj \(q\) djeluje naboj \(Q_{1}\) silom \(\vec{F}_{1}\) i naboj \(Q_{2}\) silom \(\vec{F}_{2}\). Svaku od tih sila prikazujemo Coulombovim zakonom: \[F=k\,\frac{q\,Q}{r^{2}}\] Koliki je iznos svake od tih sila i kakva je njihova orijentacija?
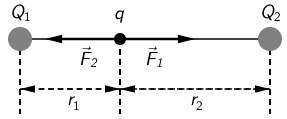
Naboji \(Q_1\) i \(Q_2\) imaju jednake predznake jer sila \(\vec{F}_{1}\) kojom naboj \(Q_1\) djeluje na naboj \(q\) mora biti suprotno orijentirana
od sile \(\vec{F}_{2}\) kojom naboj \(Q_2\) djeluje na naboj \(q\).
Sile \(\vec{F}_{1}\) i \(\vec{F}_{2}\) po iznosu moraju biti jednake.
\[k\,\frac{Q_{2}\,q}{r_{2}^{2}}=k\,\frac{Q_{1}\,q}{r_{1}^{2}}\]
\[\frac{Q_{2}}{Q_{1}}=\frac{r_{2}^{2}}{r_{1}^{2}}\]
Udaljenost naboja \(Q_2\) do točke T veća je od udaljenosti naboja \(Q_1\) do točke T:
\[r_{2}^{\,} > r_{1}^{\,}\]
Iz prethodna dva izraza slijedi:
\[Q_{2} > Q_{1}\]
Prema tome, točan odgovor je D.
11. zadatak
Dva pozitivna točkasta naboja iznosa 1 nC i 10 nC nalaze se u homogenome električnom polju
iznosa 1 N/C tako da se njihova spojnica poklapa s jednom od silnica polja. Vektor polja usmjeren je od manjega naboja
prema većemu naboju.
Koliko iznosi ukupno električno polje u točki koja se nalazi na sredini spojnice dvaju naboja ako su oni udaljeni 2 m?
- A. 10 N/C
- B. 80 N/C
- C. 90 N/C
- D. 100 N/C
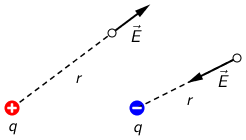
Električno polje točkastog naboja \(q\) u točki koja je za \(r\) udaljena od naboja: \[E=k\,\frac{q}{r^{2}}\]
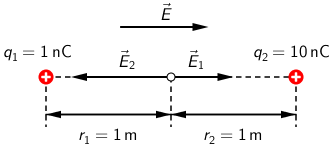
Električno polje točkastog naboja \(q_{1}\): \[E_{1}=k\,\frac{q_{1}}{r_{1}^{2}}=9\,\textrm{N}/\textrm{C}\] Električno polje točkastog naboja \(q_{2}\): \[E_{2}=k\,\frac{q_{2}}{r_{2}^{2}}=90\,\textrm{N}/\textrm{C}\] Rezultantno električno polje u točki na sredini spojnice dobit ćemo vektorskim zbrajanjem homogenog električnog polja \(\vec{E}\), koje u svim točkama ima jednaku vrijednost i električnih polja \(\vec{E}_{1}\) i \(\vec{E}_{2}\) u točki koja se nalazi na sredini spojnice naboja \(q_{1}\) i \(q_{2}\): \[E_{\textrm{r}}=E_{2}-\left (E_{1}+E\right )=80\,\textrm{N}/\textrm{C}\]
12. zadatak
Dva otpornika otpora \(4\,\Omega\) i \(6\,\Omega\) vezani su u seriju na izvor napona 12 v.
Kolika se energija utroši na otporniku od \(6\,\Omega\) tijekom jedne minute? Zanemarite unutarnji otpor izvora.
- A. 288 J
- B. 432 J
- C. 518,4 J
- D. 1440 J
Ukupni otpor serijski spojenih otpora dobiva se njihovim zbrajanjem: \[R=R_{1}+R_{2}\] Rad ili energiju električne struje prikazujemo izrazom: \[W=E=U\,I\,t\]
Krugom prolazi struja \[I=\frac{U}{R_{1}+R_{2}}=1,2\, \textrm{A}\] Prolaskom kroz otpornik od \(6\,\Omega\) struja obavi rad (utroši se energija): \[W=U\,I\,t=I^{2}\,R\,t=518,4\, \textrm{J}\]
13. zadatak
Učenik je dobio eksperimentalni zadatak u kojemu je morao istražiti ovisnost struje o naponu. Dvama otpornicima koje je imao na raspolaganju koristio se
na četiri načina. Svaki je otpornik spajao zasebno na izvor i mjerio je struju za različite vrijednosti napona. Zatim ih je spajao u seriju pa u paralelu
i mjerio je struju za različite vrijednosti napona. Dobivene podatke za svako mjerenje spojio je pravcima i prikazao u
I ,U grafu.
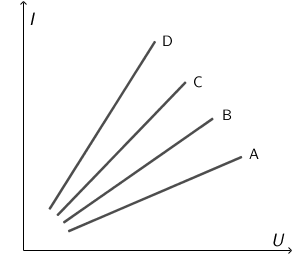
Koji od ponuđenih pravaca prikazuje serijski spoj otpornika?
- A. Pravac A.
- B. Pravac B.
- C. Pravac C.
- D. Pravac D.
Pomoć potražite na poveznici Spajanje otpora.
Otpor u krugu je najveći kada je spojio otpore serijski. Tada je struja kroz krug jednaka: \[I=\frac{U}{R_{1}+R_{2}}=\frac{1}{R_{1}+R_{2}}\,U\] Nagib pravca u I ,U grafu \[\frac{1}{R_{1}+R_{2}}\] mora biti najmanji jer je od svih kombinacija otpora nazivnik najveći za serijski spoj \(R_{1}+R_{2}\). Iz grafa vidimo da najmanji nagib ima pravac A.
14. zadatak
Homogeno magnetsko polje stalnoga iznosa usmjereno je vertikalno prema gore. U tome se polju u slobodan pad pusti horizontalno postavljena petlja
kao što je prikazano na slici.
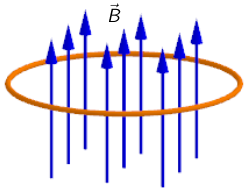
Koja je od navedenih tvrdnja istinita?
- A. U petlji se inducira struja u smjeru kazaljke na satu.
- B. U petlji se inducira struja obrnuto od smjera kazaljke na satu.
- C. Smjer inducirane struje u petlji mijenja se u vremenu.
- D. U petlji nema inducirane struje.
Prema Faradayovom zakonu elektromagnetske indukcije u petlji koja se nalazi u promjenjivom magnetskom polju inducira se elektromotorni napon: \[U_{\textrm{i}}=-\frac{\Delta \phi}{\Delta t}\]
Promjenivo magnetsko polje ostvaruje se promjenom magnetskog toka \(\Delta \phi\) kroz obruč.
U zadatku petlja pada kroz homgeno magnetsko polje pa se magnetski tok kroz obruč ne mijenja. Zato se u petlji ne inducira elektromotorni napon i
kroz nju ne prolazi struja.
Zadatak možemo riješiti i pomoću Lorentzove sile.
Brzina elektrona zbog slobodnog pada petlje usmjerena je vertikalno prema dolje pa je kut između vektora brzine elektrona i vektora magnetskog polja
\(180^{0}\). Lorentzova sila na elektrone:
\[F_{\small{\textrm{L}}}=e\,v\,B\,\textrm{sin}\, \alpha\]
također je jednaka nuli, zbog \(\textrm{sin}\, 180^{0}=0\) pa se elektroni ne mogu gibati kroz petlju i kroz nju ne prolazi struja.
15. zadatak
Tijelo ukupne energije \(E\) titra na opruzi oko ravnotežnoga položaja \(x=0\) s amplitudom \(A\).
Koliko iznosi kinetička energija tijela kada se tijelo nalazi na udaljenosti \(x=\large\frac{A}{2}\).
- A. \(E/3\)
- B. \(E/2\)
- C. \(2\,E/3\)
- D. \(3\,E/4\)
Elastična potencijalna energija tijela koje harmonijski titra: \[E_{\textrm{p,el}}=\frac{1}{2}\,k\,x^{2}\] Kinetička energija tijela koje harmonijskititra: \[E_{\textrm{k}}=\frac{1}{2}\,m\,v^{2}\] Ukupna energija harmonijskog oscilatora jednaka je zbroju elastične potencijalne i kinetičke energije tijela: \[E=E_{\textrm{p,el}}+E_{\textrm{k}}\]
U ravnotežnom položaju elastična potencijalna energija jednaka je nuli pa je ukupna energija jednaka maksimalnoj kinetičkoj energiji: \[E_{\textrm{p,el}}=0\] \[E=E_{\textrm{k,maks}}\] \[E_{\textrm{k,maks}}=\frac{1}{2}\,m\,v_{\textrm{maks}}^{2}\] \[E=\frac{1}{2}\,m\,v_{\textrm{maks}}^{2}\] U amplitudnom položaju kinetička energija je jednaka nuli pa je ukupna energija jednaka maksimalnoj elastičnoj potencijalnoj energiji: \[E_{\textrm{k}}=0\] \[E=E_{\textrm{p,maks}}\] \[E_{\textrm{p,maks}}=\frac{1}{2}\,k\,A^{2}\] \[E=\frac{1}{2}\,k\,A^{2}\qquad(1)\] Odredimo elastičnu potencijalnu energiju na udaljenosti \(x=\large\frac{A}{2}\): \[E_{\textrm{p,el}}=\frac{1}{2}\,k\,x^{2}=\frac{1}{2}\,k\,\left (A/2\right)^{2}\] \[E_{\textrm{p,el}}=\frac{1}{4}\cdot \frac{1}{2}\,k\,A^{2}\] Na osnovu izraza (1), elastičnu potencijalnu energiju možemo prikazati kao: \[E_{\textrm{p,el}}=\frac{1}{4}\,E\qquad(2)\] Iz ukupne emergije harmonijskog oscilatora \[E=E_{\textrm{p,el}}+E_{\textrm{k}}\] odredimo kinetičku energiju u trenutku kada je elongacija \(x=\large\frac{A}{2}\): \[E_{\textrm{k}}=E-E_{\textrm{p,el}}\] Uzevši u obzir izraz (2), zaključujemo: \[E_{\textrm{k}}=E-\frac{1}{4}\,E\] \[E_{\textrm{k}}=\frac{3}{4}\,E\]
16. zadatak
Ana proizvede zvuk koji se jednoliko širi u svim smjerovima i čiji intenzitet na udaljenosti 1 m iznosi
10-6 W/m2.
Koliki intenzitet zvuka čuje Stipe koji se nalazi na udaljenosti 20 m od Ane?
- A. 10-6 W/m2
- B. 10-7 W/m2
- C. 5·10-8 W/m2
- D. 2,5·10-9 W/m2
Energija \(E\) zvučnih valova koja prolazi kroz jediničnu površinu u jedinici vremena okomito na smjer širenja energije zvučnog vala zove se jakost ili intenzitet zvuka. \[I=\frac{E}{S\,t}\] Mjerna jedinica za intenzitet zvuka je: \[\textrm{W}/\textrm{m}^{2}\] Kod sfernih valova koje emitira točkasti izvor energija prolazi kroz sferu površine \[S=4\,r^{2}\,\pi\] Intenzitet kojega emitira točkasti izvor zvuka u točki koja je na udaljenosti \(r\) od izvora zvuka jednak je: \[I=\frac{E}{4\,\pi\,r^{2}\,t}\]
\[\frac{I_{1}}{I_{2}}=\frac{E}{4\,\pi\,r_{1}^{2}\,t}\cdot \frac{4\,\pi\,r_{2}^{2}\,t}{E}\] \[\frac{I_{1}}{I_{2}}=\frac{r_{2}^{2}}{r_{1}^{2}}\] \[I_{2}=\frac{r_{1}^{2}}{r_{2}^{2}}\,I_{1}=2,5\cdot 10^{-9}\,\frac{\textrm{W}}{\textrm{m}^{2}}\]
17. zadatak
Luka je od oftalmologa dobio nalaz na kojemu piše da mu trebaju naočale jakosti –2 dpt.
Kakve leće na naočalama treba nositi Luka?
- A. divergentne leće žarišne daljine 50 cm
- B. konvergentne leće žarišne daljine 50 cm
- C. divergentne leće žarišne daljine 200 cm
- D. konvergentne leće žarišne daljine 200 cm
Pomoć potražite na poveznici Primjene leća.
Jakost leće jednaka je recipročnoj vrijednosti žarišne daljine izražene u metrima: \[C=\frac{1}{f}\] \[f=\frac{1}{C}\] \[f=\frac{1}{-2}=-0,5\,\textrm{m}=-50\,\textrm{cm}\] Žarišna daljina je negativna, što znači da su leće divergentne.
Napomena
U zadatku je ispred žarišne daljine divergentne leće trebalo staviti predznak \(-\).
18. zadatak
Učenik izvodi eksperiment u kojemu laserski snop svjetlosti usmjeri na tanku vlas kose i promatra nastalu sliku na zastoru.
Koja se fizička pojava može dokazati tim eksperimentom?
- A. polarizacija svjetlosti
- B. fotoelektrični učinak
- C. disperzija svjetlosti
- D. ogib svjetlosti
U geometrijskoj optici naučili smo da se zraka svjetlosti širi pravocrtno. Ako naiđe na zapreku, očekivali bismo na zastoru oštru granicu između
svjetla i sjene. To se i događa ako je promjer zapreke velik.
Pri malim dimenzijama zapreke svjetlost će skrenuti iza zapreke u njezinu geometrijsku sjenu.
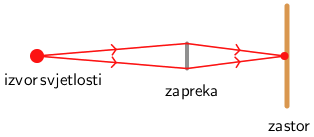
Ovu pojavu zovemo ogib ili difrakcija svjetlosti.
Eksperimentom se može dokazati ogib svjetlosti.
19. zadatak
Tijelo mase m ovješeno je na opruzi, povučeno iz ravnotežnoga položaja i u trenutku
t = 0 pušteno da titra. Frekvencija kojom tijelo titra jest f.
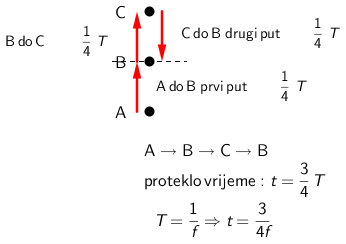
Nakon koliko vremena tijelo prolazi drugi put kroz ravnotežni položaj?
- A. 1/(4 f )
- B. 3/(4 f )
- C. 4/(3 f )
- D. 4/ f )
Pomoć potražite na poveznici Sabirne i rastresne leće.
20. zadatak
Osnovna frekvencija stojnoga vala na napetoj žici učvršćenoj na obama krajevima iznosi 340 Hz.

Kolika je frekvencija prikazanoga stojnog vala nastalog na istoj žici?
- A. 68 Hz
- B. 340 Hz
- C. 850 Hz
- D. 1700 Hz
Pomoć potražite na poveznici Stojni val na napetoj žici i u stupcu zraka.
Označimo s \(L\) duljinu žice.
Brzina vala pri osnovnoj frekvenciji
\[v=f_{0}\lambda_{0}\]
jednaka je brzini vala na crtežu
\[v=f\lambda\]
jer su valovi nastali na istoj žici. Iz ova dva izraza dobijemo:
\[f\lambda=f_{0}\lambda_{0}\]
Osnovna valna duljina je
\[\lambda_{0}=2\,L\]
Iz crteža vidimo da je
\[\lambda=L/2,5\]
Iz ova tri izraza dobijemo
\[f\cdot L/2,5=f_{0}\cdot 2\,L\]
odnosno
\[f=5\,f_{0}=1700\, \textrm{Hz}\]
21. zadatak
Učenik izvodi eksperiment u kojemu mora istražiti energiju fotoelektrona.
Što mora mjeriti da bi uspješno izveo eksperiment?
- A. temperaturu fotoelektrona
- B. razliku potencijala potrebnu za zaustavljanje fotoelektrona
- C. pomak koji fotoelektroni prijeđu u zadanome vremenu
- D. vrijeme potrebno da fotoelektroni prijeđu zadani put
Pomoć potražite na poveznici Fotoelektrični učinak.
Ako na metal kojemu je izlazni rad \(W_{0}\) padaju fotoni energije \(E_{\textrm{f}}=h\,f\), dolazi do izbacivanja elektrona iz metala. Najveća kinetička energija tih fotoelektrona (Einsteinova jednadžba za fotoefekt) je: \[E_{\textrm{k}}=E_{\textrm{f}}-W_{0}\] Te je elektrone moguće zaustaviti električnim poljem kojemu možemo mijenjati napon. U jednom se trenutku elektroni zaustave, što znači da im je kinetička energija jednaka nuli. Električno polje obavilo je rad \(W=e\,U\) za zaustavljanje fotoelektrona: \[E_{\textrm{k}}=e\,U\] Uz poznati napon (razliku potencijala) možemo odrediti kinetičku energiju najbržih fotoelektrona.
22. zadatak
Svemirski brod u obliku kugle giba se brzinom 0,95 c u odnosu na promatrača na Zemlji kao što je prikazano na slici.
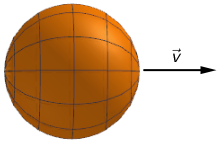
Koji oblik svemirskoga broda mjeri promatrač sa Zemlje?
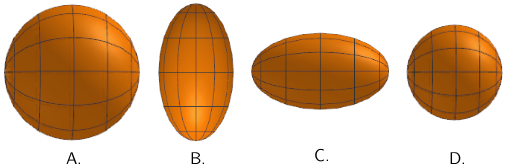
- A. slika A.
- B. slika B.
- C. slika C.
- D. slika D.
Pomoć potražite na poveznici Kontrakcija duljine.
Kontrakcija duljine: \[L=L_{0}\sqrt{1-u^2/c^2}\] Skraćuju se samo duljine u smjeru gibanja, dok se duljine koje su na taj smjer okomite ne skraćuju. Točan odgovor je B.
23. zadatak
Kolika je najmanja energija potrebna za ionizaciju atoma vodika koji se nalazi u osnovnome stanju?
- A. 10,21 eV
- B. 12,75 eV
- C. 13,06 eV
- D. 13,60 eV
Energije vodikovog atoma, prema Bohru, mogu poprimiti vrijednosti: \[E_{n}=-\frac{k^{2}\,m\,e^{4}}{2\,n^{2}\,\hbar^{2}}\] Energiju osnovnog stanja dobijemo ako u prethodni izraz uvrstimo \(n=1\).
Energija osnovnog stanja vodikovog atoma: \[E_{1}=-\frac{k^{2}\,m\,e^{4}}{2\,\hbar^{2}}=-2,18\cdot{10}^{-18}\,\textrm{J}\] \[E_{1}=-13,6\ \textrm{eV}\]
Napomena
Energije vodikovog atoma su negativne pa je u ponuđenim odgovorima trebalo staviti predznak minus.
24. zadatak
U posudi se nalazi voda na čijoj površini pluta kuglica tako da je polovina obujma kuglice uronjena u vodu. Koja je od navedenih tvrdnja ispravna ako se na površinu vode dolije ulje? Pretpostavite da se voda i ulje ne miješaju. Gustoća kuglice veća je od gustoće ulja, a manja od gustoće vode.
- A. Više od polovine obujma kuglice uronjeno je u vodu.
- B. Polovina obujma kuglice uronjena je u vodu.
- C. Manje od polovine obujma kuglice uronjeno je u vodu.
Pomoć potražite na poveznici Sila na uronjeno tijelo-uzgon.
Uzgon prikazujemo izrazom: \[F_{\textrm{u}}=\rho\,g\,V\]
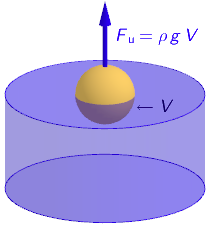
- \(\rho\) - gustoća fluida (vode)
- \(g\) - akceleracija slobodnog pada
- \(V\) - Volumen uronjenog dijela tijela
Napomena
Točan račun pokazuje da bi gustoća ulja morala biti manja od \(500\,\textrm{kg}/\textrm{m}^{3}\), ali takvo ulje ne postoji.
25. zadatak
Zbog čega se papirnata čaša tankih stijenki napunjena vodom ne zapali kada ju stavimo na plamenik?
- A. jer toplina s plamenika prelazi samo na vodu
- B. jer papir ima veći specifični toplinski kapacitet od vode
- C. jer papirnata čaša ne može poprimiti višu temperaturu od vode
Pomoć potražite na poveznici Magnetska sila između dvije paralelne strujne žice.
Tijela koja se nalaze u toplinskom kontaktu nakon nekog vremena poprime jednaku temperaturu – papir ima temperaturu kao i voda.
Točan odgovor je C.
26. zadatak
Marko je planinareći po Biokovu naišao na duboku jamu.
Koliko je duboka jama ako je Marko čuo odjek svojega glasa nakon 4,6 s?
Brzina zvuka u zraku iznosi 340 m/s.
Odgovor: m
Pomoć potražite na poveznici: Opći zakon gravitacije.
Vrijeme potrebno da zvuk dođe do dna jame je: \[t=\frac{4,6}{2}=2,3\,\textrm{s}\] Dubina jame je: \[h=v\cdot t=782\,\textrm{m}\]
27. zadatak
Balon napunjen plinom pri normiranim uvjetima podigne se u atmosferu do visine na kojoj je tlak
8·104 Pa.
Koliko se puta volumen balona poveća ako pretpostavimo da se temperatura nije promijenila?
Volumen se poveća: puta.
Pomoć potražite na poveznici: Izotermna promjena stanja plina.
- \(p_{0}^{\,}=101325\,\textrm{Pa}\)
- \(T_{0}^{\,}=273,15\,\textrm{K}\)
Izotermna promjena stanja plina: \[p_{0}^{\,}\,V_{0}^{\,}=p\,V\] \[\frac{V}{V_{0}}=\frac{p_{0}^{\,}}{p}\] \[\frac{V}{V_{0}}=1,27\]
28. zadatak
Ploče pločastoga kondenzatora udaljene su 1 mm u vakuumu.
Koliki je kapacitet kondenzatora ako je površina pojedine ploče 10 dm2?
Odgovor: pF
Kapacitet pločastog kondenzatora: \[C=\varepsilon_{0}\,\varepsilon_{r}\,\frac {S}{d}\]
- \(\varepsilon_{0}\) - permitivnost vakuuma
- \(\varepsilon_{r}\) - permitivnost sredstva između ploča kondenzatora
- \(S\) - površina ploče kondenzatora
- \(d\) - udaljenost između ploča
Kapacitet pločastog kondenzatora u vakuumu je: \[C=\varepsilon_{0}\,\frac{S}{d}\] \[C=8,85\cdot 10^{-12}\,\textrm{F}\] \[C=8,85\,\textrm{pF}\]
29. zadatak
Promatrač na obali izmjeri da je frekvencija zvuka koji emitira brodska sirena 875 Hz, dok kapetan toga broda izmjeri
da je frekvencija zvuka brodske sirene 900 Hz.
Kolikom se brzinom brod udaljava od obale? Brzina zvuka u zraku iznosi 340 m/s.
Odgovor: m/s
Pomoć potražite na poveznici: Dopplerov učinak.
Izraz za Dopplerov učinak nalazi se i u knjižici formula: \[f_{\textrm{s}}=f_{\textrm{i}}\,\frac{v+v_{\textrm{s}}}{v-v_{\textrm{i}}}\] Brzina slušatelja (promatrač na obali) je nula \(v_{\textrm{s}}=0\), a brzina izvora zvuka (brod) je negativna jer se brod udaljava. \[f_{\textrm{s}}=f_{\textrm{i}}\,\frac{v}{v+v_{\textrm{i}}}\] \[v_{\textrm{i}}=v\,\left(\frac{f_{\textrm{i}}}{f_{\textrm{s}}}-1\right)=9,71\,\textrm{m}/\textrm{s}\]
30. zadatak
Aktivnost uzorka nekoga radioaktivnog elementa iznosi 400 Bq. Nakon 6 sati aktivnost istoga uzorka
iznosi 25 Bq.
Koliko je vrijeme poluraspada toga uzorka?
Odgovor: h
Pomoć potražite na poveznici: Zakon radioaktivnog raspada.
Izraz za aktivnost je analogan izrazu za broj neraspadnutih jezgri pri radioaktivnom raspadu: \[A=A_{0}\,e^{\Large{-\textrm{ln}\left(2\right)\, \frac{t}{T}}}\] \[-\textrm{ln}\left(2\right)\,\frac{t}{T}=\textrm{ln}\,\left(\frac{A}{A_{0}}\right)\] \[\frac{t}{T}=4\] \[T=\frac{t}{4}=1,5\, \textrm{h}\]
31. zadatak
Automobil mase 850 kg zaustavio se uslijed kvara na horizontalnoj cesti. Dva čovjeka pokušavaju ga gurati tako da djeluju
paralelnim silama iste orijentacije. Jedan djeluje silom 275 N, a drugi silom 395 N na automobil.
Sila trenja između ceste i automobila iznosi 560 N.
Koliko iznosi akceleracija automobila?
Odgovor: m/s2
Odredimo iznos rezultantne sile i primijenimo drugi Newtonov zakon.

\[F=F_{1}+F_{2}-F_{\textrm{t}}=275+395-560=110\, \textrm{N}\] \[a=\frac{F}{m}=0,129\, \frac{\textrm{m}}{\textrm{s}^2}\]
32. zadatak
Koliku snagu mora imati grijač kako bi 250 g vode temperature 100 0C
isparilo za 1 h ako se sva energija grijača upotrebljava za zagrijavanje vode?
Specifična toplina isparavanja vode je 2,26 MJ/kg.
Odgovor: W
Pomoć potražite na poveznici: Promjena agregatnih stanja tvari.
Specifična toplina isparavanja: \[Q_{\textrm{i}}=r\,m\] Snaga grijača: \[P=\frac{Q_{\textrm{i}}}{t}\] \[P=\frac{r\,m}{t}=156,9\, \textrm{W}\]
33. zadatak
Kada se u strujni krug spoji otpor od 1 Ω, pad napona na krajevima izvora iznosi 2 V.
Kada se spoji otpor od 2 Ω, pad napona na krajevima izvora iznosi 2,4 V.
Koliki je unutarnji otpor izvora?
Odgovor: \(\Omega\)
Ohmov zakon za dio strujnog kruga: \[I=\frac{U}{R}\]
- \(R\) - otpor otpornika
- \(U\) - napon (pad napona) na krajevima otpornika
- \(\varepsilon\) - elektromotorni napon izvora struje
- \(R_{\textrm{u}}\) - unutarnji otpor izvora struje
- \(R\) - otpor u strujnom krugu
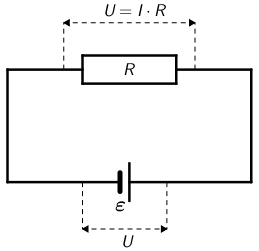
Pad napona na vanjskom otporu jednak padu napona na krajevima izvora. Struje koje prolaze kroz otpore \(R_{1}\) i \(R_{2}\) odredimo na osnovu Ohmovog zakona za dio strujnog kruga: \[I_{1}=\frac{U_{1}}{R_{1}}=2\,\textrm{A}\] \[I_{2}=\frac{U_{2}}{R_{2}}=1,2\,\textrm{A}\] Na osnovu Ohmovog zakona za cijeli strujni krug \[I=\frac{\varepsilon}{R_{\textrm{u}}+R}\] zaključujemo da elektromotorni napon možemo prikazati kao \[\varepsilon=I\,\left(R_{\textrm{u}}+R\right)\] Uvrstimo podatke za oba otpora \[\varepsilon=2\,\left(R_{\textrm{u}}+1\right)\] \[\varepsilon=1,2\,\left(R_{\textrm{u}}+2\right)\] Izjednačimo desne strane ovih izraza \[2\,\left(R_{\textrm{u}}+1\right)=1,2\,\left(R_{\textrm{u}}+2\right)\] \[R_{\textrm{u}}=0,5\, \Omega\]
34. zadatak
Djevojčica mase 34 kg sjedi na lopti tako da je lopta potpuno uronjena u vodu.
Koliki je polumjer lopte? Ukupna masa lopte iznosi 200 g. Zanemarite silu uzgona na djevojčicu.
Odgovor: m
Koje sve sile djeluju na loptu? Kolika je rezultanta svih sila ako lopta lebdi odmah ispod površine vode?
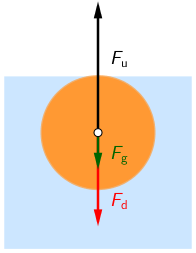
Na loptu djeluje djevojčica svojom težinom \(F_{\textrm{d}}\) i sila teža \(F_{\textrm{g}}\).
Lopta lebdi u vodi pa je ukupna sila na nju jednaka nuli. Zbog toga je iznos uzgona na loptu jednak zbroju iznosa težine djevojčice i sile teže
koja djeluje na loptu.
\[F_{\textrm{u}}=F_{\textrm{d}}+F_{\textrm{g}}\]
\[\rho g\,V=m_{\textrm{d}\,}g+m_{\small{\textrm{L}}}\,g\]
\[V=\frac{m_{\textrm{d}}+m_{\small{\textrm{L}}}}{\rho}=0,0342\,\textrm{m}^{3}\]
\[V=\frac{4}{3}\,r^{3}\,\pi\Rightarrow r=0,20\,\textrm{m}\]
35. zadatak
Proton uleti brzinom 100 m/s u homogeno magnetsko polje iznosa 0,2 mT. Vektor
brzine i vektor polja zatvaraju kut od 600.
Koliko punih namotaja spirale napravi proton dok se pomakne 1 m u smjeru polja?
Odgovor:
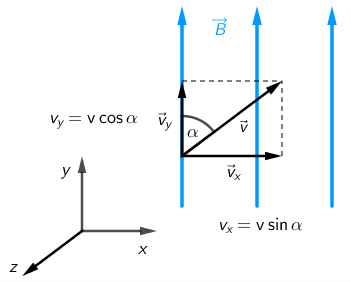
Rastavimo brzinu protona na vertikalnu \(v_{y}\) i horizontalnu \(v_{x}\) komponentu. Zbog komponente \(v_{x}\) proton bi se gibao jednoliko po kružnici u ravnini okomitoj na magnetsko polje, dok bi se zbog komponente \(v_{y}\) proton gibao jednoliko po pravcu u smjeru magnetskog polja. Stvarno gibanje bit će složeno od ova dva gibanja pa će se proton gibati po spirali.
Na proton u horizontalnom smjeru djeluje Lorentzova sila \[F_{\small{\textrm{L}}}=e\,v_{x}\,B\, \textrm{sin}\, 90^{0}=e\,v_{x}\,B\qquad(1)\] jer su vektori \(\vec{v}_{x}\) i \(\vec{B}\) okomiti. Ta sila ima ulogu centripetalne sile \[F_{\textrm{c}}=\frac{m\,v_{x}^{2}}{r}\qquad(2)\] Izjednačimo izraz (2) s izrazom (1) i odredimo komponentu brzine \(v_{x}\): \[e\,v_{x}\,B=\frac{m\,v_{x}^{2}}{r}\Rightarrow v_{x}=\frac{e\,B\,r}{m}\qquad(3)\] Brzina jednolikog gibanja po kružnici jednaka je: \[v_{x}=\frac{2\,r\,\pi}{T}\qquad(4)\] Izjednačavanjem izraza (3) i (4) za ophodno vrijeme dobijemo: \[T=\frac{2\,\pi\,m}{e\,B}\] U vertikalnom smjeru proton će prijeći put \(s\) za vrijeme \[t=\frac{s}{v_{y}}=\frac{s}{v\,\textrm{cos}\,\alpha}\] Broj punih okreta jednak je \[n=\frac{t}{T}=\frac{s\,e\,B}{2\,\pi\,m\,v\,\textrm{cos}\,\alpha}=60\]
36. zadatak
Stakleni kvadar nalazi se na stolu. Snop svjetlosti iz laserskoga pokazivača upada
na "gornju" površinu kvadra pod kutom od 700. Zraka svjetlosti prolazi kroz kvadar
i na okomitu stranu upada pod graničnim kutom totalne refleksije.
Koliko iznosi indeks loma stakla od kojega je kvadar načinjen?
Odgovor:
Primijenite zakon loma na "gornjoj" i na "bočnoj" strani staklenog kvadra.
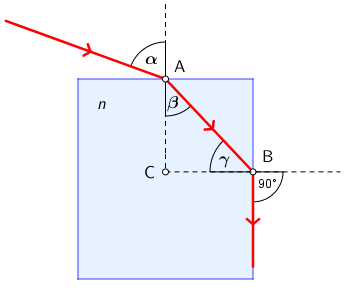
Zakon loma u točki A: \[n_{\textrm{z}}\cdot\textrm{sin}\,\alpha=n\cdot \textrm{sin}\, \beta\] Indeks loma zraka: \[n_{\textrm{z}}\approx 1\] \[\textrm{sin}\,\alpha=n\cdot \textrm{sin}\, \beta\qquad(1)\] Zraka svjetlosti upada na bočnu plohu u točki B pod graničnim kutom: \[n\cdot \textrm{sin}\, \gamma=1\qquad(2)\] Iz trokuta ABC vidimo da je \[\gamma=90^{0}-\beta\qquad(3)\] Izraz (3) uvrstimo u izraz (2): \[n\cdot \textrm{sin}\,\left (90^{0}-\beta\right )=1\] \[n\cdot \textrm{cos}\,\beta=1\qquad(4)\] Kvadrirajmo izraz (1): \[\textrm{sin}^{2}\,\alpha=n^{2}\cdot\textrm{sin}^{2}\,\beta\Rightarrow \textrm{sin}^{2}\,\beta=\frac{\textrm{sin}^{2}\alpha}{n^{2}}\qquad(5)\] Kvadrirajmo izraz (4): \[n^{2}\cdot\textrm{cos}^{2}\,\beta=1\Rightarrow \textrm{cos}^{2}\,\beta=\frac{1}{n^{2}}\qquad(6)\] Zbrojimo izraze (5) i (6): \[\frac{\textrm{sin}^{2}\,\alpha}{n^{2}}+\frac{1}{n^{2}}=1\] Traženi indeks loma jednak je: \[n=\sqrt{\textrm{sin}^{2}\,\alpha+1}\] \[n=1,37\]
37. zadatak
Kolika je valna duljina elektrona ubrzanoga iz stanja mirovanja razlikom potencijala 120 V?
Odgovor: m
Primijenite izraz za de Broglievu valnu duljinu i rad električnog polja koji se pretvara u kinetičku energiju elektrona.
De Broglieva valna duljina elektrona jednaka je \[\lambda=\frac{h}{p}\qquad(1)\] Za ubrzavanje elektrona električno polje izvršilo je rad \[W=e\,U\] koji se pretvorio u kinetičku energiju elektrona \[E_{\textrm{k}}=\frac{m\,v^{2}}{2}\] Iz \(W=E_{\textrm{k}}\) dobijemo \[e\,U=\frac{m\,v^{2}}{2}\] Razlomak proširimo s \(m\) \[e\,U=\frac{m^{2}\,v^{2}}{2\,m}\qquad(2)\] U brojniku je kvadrat količine gibanja \(p=m\,v\) pa izraz (2) prikažimo kao \[e\,U=\frac{p^{2}}{2\,m}\Rightarrow p=\sqrt{2\,m\,e\,U}\qquad(3)\] Izraz (3) uvrstimo u izraz (1): \[\lambda=\frac{h}{\sqrt{2\,m\,e\,U}}=1,12\cdot 10^{-10}\,\textrm{m}\]