Ljetni rok 2023. godine
1. zadatak
Na slici je prikazan \(x,t\) graf gibanja autića.
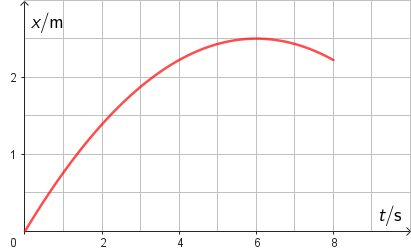
Koja je od navedenih tvrdnja o gibanju autića točna?
- A. Autić ima stalnu akceleraciju tijekom cijeloga puta.
- B. Autić postigne najveću brzinu nakon šest sekunda.
- C. Autić prijeđe ukupni put jednak površini ispod x, t grafa.
- D. U šestoj sekundi autić prijeđe veći put nego u prvoj sekundi.
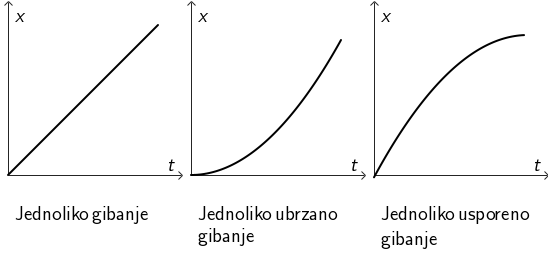
Zadani \(x,t\) graf je parabola koja odgovara jednolikom usporenom gibanju. Kod jednoliko usporenog, a također i jednoliko ubrzanog gibanja, iznos akceleracije je konstantan. Točan je odgovor A.
2. zadatak
Na slici su prikazana dva tijela, T1 i T2.
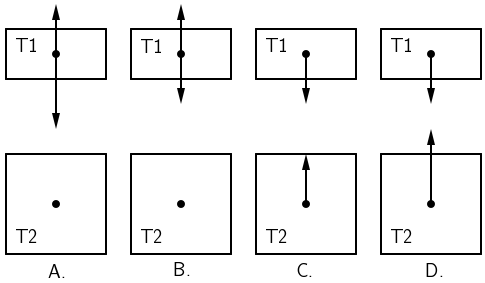
Na kojoj su od ponuđenih slika ispravno prikazane sile kojima tijela međudjeluju?
- A. Slika A.
- B. Slika B.
- C. Slika C.
- D. Slika D.
Primijenite 3. Newtonov zakon.
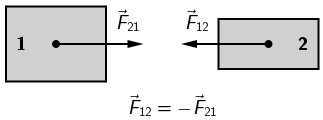
Sile kojima međudjeluju dva tijela imaju jednak smjer, suprotnu orijentaciju i jednak im je iznos. Slika C je točan odgovor.
3. zadatak
Ukupnim impulsom sile I tijelo mase m pokrene se iz mirovanja tako da na kraju djelovanja ima kinetičku
energiju Ek.
Kolika će biti kinetička energija tijela mase 2m ako se to tijelo iz mirovanja pokrene ukupnim impulsom sile
I / 2?
- A. 2Ek
- B. Ek
- C. Ek / 2
- D. Ek / 8
Impuls sile koja djeluje na tijelo jednak je umnošku sile i intervala vremena u kojem je sila djelovala na tijelo: \[I=F\,\Delta t\] Iz temeljnog zakona gibanja: \[F=m\,a=m\,\frac{\Delta v}{\Delta t}\] slijedi da je impuls sile jednak promjeni količine gibanja tijela: \[F\,\Delta t = m\,\Delta v\] \[F\,\Delta t = m\left(v_{\textrm{kon}}-v_{\textrm{poc}}\right)\] \[F\,\Delta t = m\,v_{\textrm{kon}}-m\,v_{\textrm{poc}}\] Znak za količinu gibanja je \(p\,\): \[F\,\Delta t = p_{\textrm{kon}}-p_{\textrm{poc}}\]
Impuls sile djelovao je na tijelo koje u početku miruje: \[I=p_{\textrm{kon}}-0=p=m\,v\] Kinetičku energiju tijela: \[E_{\textrm{k}}=\frac{m\,v^{2}}{2}\] možemo prikazati pomoću količine gibanja, odnosno impulsa, ako razlomak proširimo s \(m\,\): \[E_{\textrm{k}}=\frac{m^{2}\,v^{2}}{2\,m}=\frac{p^{2}}{2\,m}\] \[E_{\textrm{k}}=\frac{I^{2}}{2\,m}\] Ako na tijelo mase \(2\,m\) djeluje impuls \(I/2\), njegova će kinetička energija biti: \[E_{\textrm{k,1}}=\left(\frac{I}{2}\right)^{2}\cdot\frac{1}{2\cdot 2\,m}\] \[E_{\textrm{k,1}}=\frac{I^{2}}{4}\cdot\frac{1}{2\cdot 2\,m}\] \[E_{\textrm{k,1}}=\frac{1}{8}\cdot \frac{I^{2}}{2\,m}\] \[E_{\textrm{k,1}}=\frac{1}{8}\cdot E_{\textrm{k}}=\frac{E_{\textrm{k}}}{8}\] Točan odgovor je D.
4. zadatak
Svemirski brod nalazi se na pravcu koji prolazi kroz središta planeta X i Y. Središta planeta međusobno su udaljena 1500 milijuna kilometara.
Masa planeta Y 4 je puta veća od mase planeta X.
Na kojoj se udaljenosti od planeta X nalazi svemirski brod kad je ukupna gravitacijska sila planeta X i Y na njega jednaka nuli?
- A. 375 milijuna kilometara
- B. 500 milijuna kilometara
- C. 750 milijuna kilometara
- D. 1125 milijuna kilometara
Primijenimo Newtonov zakon gravitacije.
Dva tijela, čija su središta udaljena \(r\) i kojima su mase \(m_{1}\) i \(m_{2}\), privlače se gravitacijskom silom \(F\):
\[F=G\,\frac {m_{1}\,m_{2}}{r^{2}}\]
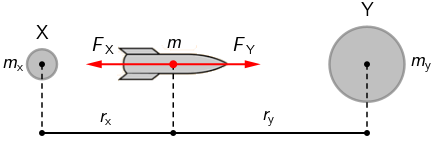
Planet X na svemirski brod djeluje gravitacijskom silom:
\[F_{\small{\textrm{X}}}=G\,\frac {m\,m_{\textrm{x}}}{r^{\;2}_{\textrm{x}}}\]
Planet Y na svemirski brod djeluje gravitacijskom silom:
\[F_{\small{\textrm{Y}}}=G\,\frac {m\,m_{\textrm{y}}}{r^{\;2}_{\textrm{y}}}\]
Ukupna sila jednaka je nuli pa zato sile \(F_{\small{\textrm{X}}}\) i \(F_{\small{\textrm{Y}}}\)
po iznosu moraju biti jednake:
\[G\,\frac {m\,m_{\textrm{x}}}{r^{\;2}_{\textrm{x}}}=G\,\frac {m\,m_{\textrm{y}}}{r^{\;2}_{\textrm{y}}}\]
Pojednostavnimo ovaj izraz i uzmimo u obzir da je \(m_{\textrm{y}}=4\,m_{\textrm{x}}\,\):
\[\frac {m_{\textrm{x}}}{r^{\;2}_{\textrm{x}}}=\frac {4\,m_{\textrm{x}}}{r^{\;2}_{\textrm{y}}}\]
\[r^{\;2}_{\textrm{x}}=\frac{r^{\;2}_{\textrm{y}}}{4}\]
\[r_{\textrm{x}}=\frac{r_{\textrm{y}}}{2}\]
Uzmimo u obzir pretpostavku u zadatku:
rx + ry = 1500 milijuna km.
Iz prethodna dva izraza dobivamo za udaljenost svemirskog broda od planeta X:
rx = 500 milijuna km.
5. zadatak
Učenica prilikom zarona u more mjeri ovisnost ukupnoga tlaka p o dubini d.

Koji od ponuđenih grafova ispravno prikazuje njezino mjerenje?
- A. Graf A.
- B. Graf B.
- C. Graf C.
- D. Graf D.
Ukupni tlak na dubini h u moru bit će jednak zbroju atmosferskog i hidrostatskog tlaka na toj dubini: \[p=p_{\textrm{a}}+p_{\textrm{h}}=p_{\textrm{a}}+\rho\,g\,h\]
Tlak na površini mora jednak je atmosferskom tlaku. Ako učenica zaroni, tlak se povećava sa dubinom. Ukupni je tlak jednak: \[p=p_{\textrm{a}}+\rho\,g\,d\] Grafički prikaz ovog izraza odgovara grafu C.
6. zadatak
Na kojoj će temperaturi aluminijska šipka biti 0,5 % dulja nego na temperaturi 10 oC?
Koeficijent je linearnoga toplinskog rastezanja aluminija je 2,6 · 10 -5 K-1.
- A. 182 oC
- B. 192 oC
- C. 202 oC
- D. 212 oC
Linearno toplinsko širenje šipke, štapa ili žice: \[\ell_{2}=\ell_{1}\cdot\left(1+\alpha\,\Delta t\right)\]
Linearno toplinsko širenje aluminijske šipke prikažimo u obliku: \[\ell_{2}=\ell_{1}\cdot\left[1+\alpha\,\left(t_{2}-t_{1}\right)\right]\] \[\ell_{2}=1,005\,\ell_{1}\] \[1,005\,\ell_{1}=\ell_{1}\cdot\left[1+\alpha\,\left(t_{2}-t_{1}\right)\right]\] \[1+\alpha\,\left(t_{2}-t_{1}\right)=1,005\] \[t_{2}-t_{1}=\frac{0,005}{\alpha}\] \[t_{2}=\frac{0,005}{\alpha}+t_{1}\] \[t_{2}=\frac{0,005}{2,6\cdot 10^{-5}}+10\] \[t_{2}=202,31\, ^{\textrm{o}}\textrm{C}\]
7. zadatak
U čvrstoj boci nalazi se idealni plin pod tlakom p.
Koliki će biti tlak plina u boci kad se iz boce ispusti jedna četvrtina mase plina, a termodinamička se temperatura plina dvostruko poveća?
- A. 3p / 4
- B. 3p / 2
- C. p / 2
- D. p / 4
Jednadžbu stanja idealnog plina: \[pV=n\,R\,T\] zapišimo u obliku: Broj molova plina jednak je masi plina podijeljenoj s molarnom masom: \[n=\frac{m}{M}\]
Jednadžbu stanja idealnog plina zapišimo u obliku: \[p\,V=\frac{m}{M}\,R\,T\quad(1)\] Ako iz boce ispustimo jednu četvrtinu mase plina, a temperaturu povećamo dva puta, jednadžba stanja će biti: \[p_{_{\large{2}}}\,V=\frac{3\,m}{4\,M}\,R\cdot 2\cdot T\] \[p_{_{\large{2}}}\,V=\frac{3\,m}{4\,M}\,R\cdot 2\cdot T\] \[p_{_{\large{2}}}\,V=\frac{3}{2}\cdot \frac{m}{M}\,R\,T\quad(2)\] Podijelimo jednadžbu (2) s jednadžbom (1): \[\frac{p_{_{\large{2}}}}{p}=\frac{3}{2}\Rightarrow p_{_{\large{2}}}=\frac{3}{2}\,p \]
8. zadatak
Zrak je smjesa različitih plinova s najvećim udjelom dušika i kisika. Ljeti su prosječne temperature zraka veće nego zimi.
Koja je od navedenih tvrdnja o odnosu prosječnih kinetičkih energija molekula dušika i kisika točna? Pretpostavite da je zrak idealni plin.
- A. Prosječna kinetička energija molekula kisika uvijek je veća od prosječne kinetičke energije molekula dušika.
- B. Prosječna kinetička energija molekula kisika uvijek je manja od prosječne kinetičke energije molekula dušika.
- C. Prosječna kinetička energija molekula kisika i dušika međusobno je jednaka, no ljeti je veća nego zimi.
- D. Prosječna kinetička energija molekula kisika i dušika međusobno je jednaka, no zimi je veća nego ljeti.
Molekule jednoatomnog idealnog plina mogu se gibati samo translacijski. Njihova srednja kinetička energija je:
\[\bar{E_{\textrm{k}}}=\frac{3}{2}kT\]
Molekule dvoatomnih plinova, osim translacijskog gibanja, mogu i rotirati pa je njihova srednja kinetička energija veća:
\[\bar{E_{\textrm{k}}}=\frac{5}{2}kT\]
Srednja kinetička energija molekula proporcionalna je temperaturi plina.
Iz navedenih izraza vidimo da srednja kinetička energija molekula ne ovisi o njihovoj masi nego samo o temperaturi.
Molekule svih jednoatomnih idealnih plinova pri jednakoj temperaturi imaju jednaku srednju kinetičku energiju iako se mase molekula razlikuju.
Isti zaključak vrijedi i za srednju kinetičku energiju molekula dvoatomnog idealnog plina. Pri jednakoj temperaturi srednja kinetička energija
molekule kisika jednaka je srednjoj kinetičkoj energiji molekule dušika iako je masa molekule kisika veća od mase molekule dušika.
Srednja kinetička energija proporcionalna je apsolutnoj temperaturi i zato će ljeti biti veća nego zimi.
Točan odgovor je C.
9. zadatak
Idealni plin nalazi se u cilindru s pomičnim klipom.
Kako će se promijeniti tlak i temperatura plina pri adijabatskoj kompresiji?
- A. Tlak i temperatura se smanje.
- B. Tlak i temperatura se povećaju.
- C. Tlak se smanji, a temperatura se poveća.
- D. Tlak se poveća, a temperatura se smanji.
U adijabatskom procesu plin ne izmjenjuje toplinu s okolinom.

Iz p,V grafa vidimo da se kompresijom plina od početnog do konačnog volumena
tlak plina povećava.
Mogli bismo iz grafa odrediti početni i konačni volumen i tlak pa primijeniti jednadžbu stanja idealnog plina, iz koje bismo zaključili da se pri adijabatskoj
kompresiji temperatura plina povećava. (Pri adijabatskoj ekspanziji temperatura plina se smanjuje.)
Točan odgovor je B.
10. zadatak
Na slici je prikazan kružni proces kroz koji prolazi neki idealni plin.
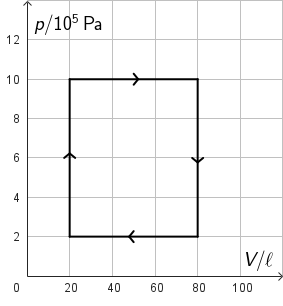
Koliko iznosi ukupni rad tijekom ovoga kružnog procesa?
- A. 0 J
- B. 12 kJ
- C. 48 kJ
- D. 60 kJ
Iz p,V grafa rad određujemo kao površinu lika kojega omeđuje graf.
\[W=\Delta p\cdot \Delta V\] \[W=8\cdot 10^{5}\cdot 60\cdot 10^{-3}\] \[W=48 000\, \textrm{J}=48\,\textrm{kJ}\]
11. zadatak
Na četiri slike prikazana su po dva električna naboja na određenim udaljenostima.
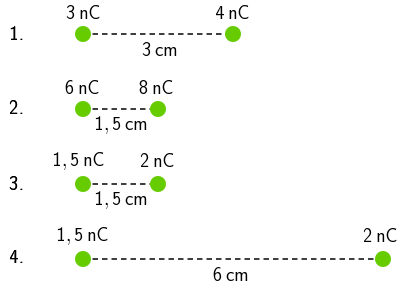
Na kojim su slikama električne sile između naboja jednakih iznosa?
- A. 1. i 2.
- B. 1. i 3.
- C. 2. i 3.
- D. 2. i 4.
Električna sila između dva točkasta ili sferno simetrična naboja može se prikazati pomoću Coulombovog zakona: \[F=k\,\frac{q_{1}\cdot q_{2}}{r^{2}}\]
Električnu silu između dva naboja napišimo u obliku proporcionalnosti: \[F=\sim\frac{q_{1}\cdot q_{2}}{r^{2}}\] Sada ne moramo pretvarati nanokulone u kulone ni centimetre u metre. Konstanta proporcionalnosti razlikovat će se od Coulombove konstante, ali će u sva četiri slučaja imati jednaku vrijednost.
- \[F_{1}=\sim\frac{3\cdot 4}{3^{2}}=\frac{12}{9}=\frac{4}{3}\]
- \[F_{2}=\sim\frac{6\cdot 8}{1,5^{2}}=\frac{48}{2,25}=\frac{4800}{225}=\frac{64}{3}\]
- \[F_{3}=\sim\frac{1,5\cdot 2}{1,5^{2}}=\frac{3}{2,25}=\frac{300}{225}=\frac{4}{3}\]
- \[F_{4}=\sim\frac{1,5\cdot 2}{6^{2}}=\frac{3}{36}=\frac{1}{12}\]
12. zadatak
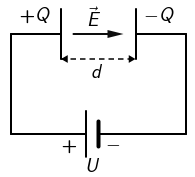
Kondenzator na svojim pločama nosi naboje iznosa +Q i -Q kad je spojen na bateriju napona
U. Iznos je električnoga polja među pločama E. Spojna žica pozitivne ploče kondenzatora prespoji se na negativni pol
baterije, a spojna žica negativne ploče kondenzatora prespoji se na pozitivni pol baterije.
Za koliko se zbog toga promijeni iznos električnoga polja među pločama kondenzatora?
- A. za 0
- B. za E / 2
- C. za E
- D. za 2 E
Električno polje između ploča kondenzatora, koje su udaljene za d jedna od druge, spojenog na napon U, po iznosu je jednako: \[E=\frac{U}{d}\]
Električno polje između ploča kondenzatora homogeno je i orijentirano je od pozitivne ka negativnoj ploči. Iznos tog električnog polja je: \[E=\frac{U}{d}\]
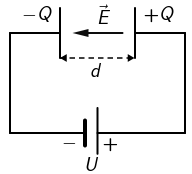
Ako zamijenimo polaritet baterije, orijentacija električnog polja postat će suprotna, dok se iznos električnog polja neće promijeniti. Točan odgovor je A.
13. zadatak
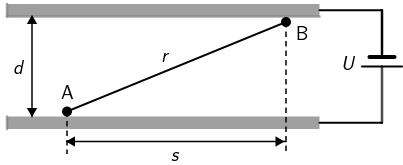
Proton se premješta vanjskom silom F od točke A do točke B između dviju metalnih nabijenih ploča međusobno razmaknutih za d kao što je prikazano na slici. Horizontalna udaljenost između točaka A i B iznosi s, a najkraća udaljenost između točaka iznosi r.
Koliki je iznos rada koji obavi sila F koja djeluje na proton dok ga premjesti od točke A do točke B u tome električnom polju?
- A. F r
- B. F s
- C. F d
- D. 0
Homogeno električno polje
Homogeno električno polje u svakoj točki ima jednak smjer, orijentaciju i iznos.
Električno polje između dvije ravne ploče, u točkama koje su daleko od rubova ploče je homogeno.
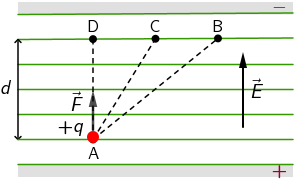
Sila kojom električno polje djeluje na proton je stalna i može se prikazati kao: \[F=q\,E\] Rad kojeg obavi električno polje za premještanje protona iz točke A u točku D jednak je: \[W_{\textrm{AD}}=F\,d =q\,E\,d\] \(E\,d\) je napon između točaka A i D:
\[U_{\textrm{AD}}=E\,d\] Prema tome, rad električnog polja možemo prikazati i kao: \[W_{\textrm{AD}}=q\,U_{\textrm{AD}}\]
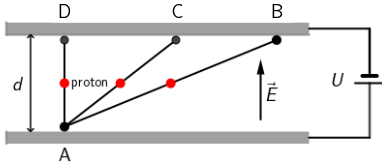
Rad kojega obavi električno polje pri premještanju protona iz točke A u točku D: \[W_{\textrm{AD}}=q\,U_{\textrm{AD}}\] Napon između dvije točke električnog polja jednak je razlici potencijala električnog polja u tim točkama: \[U_{\small{\textrm{AD}}}=\varphi_{\small{\textrm{D}}}-\varphi_{\small{\textrm{A}}}\] \[W_{\textrm{AD}}=q\,\left(\varphi_{\small{\textrm{D}}}-\varphi_{\small{\textrm{A}}}\right)\] Točke D, C i B imaju jednak potencijal pa je rad kojega obavi sila F pri prenošenju protona iz točke A u točku D, C ili B jednak: \[W_{\textrm{AD}}=W_{\textrm{AC}}=W_{\textrm{AB}}\] Pokazali smo da je: \[W_{\textrm{AD}}=F\,d\] pa je i rad \[W_{\textrm{AB}}=F\,d\]
14. zadatak
Na žarulji Ž1 stoji oznaka 100 W i 230 V, a na žarulji Ž2 40 W i 230 V.
Žarulje se prvo spajaju paralelno, a zatim serijski na izmjenični izvor napona 230 V.
Koja je od navedenih tvrdnja točna za sjaj žarulja u navedenim spojevima?
- A. I u paralelnome i u serijskome spoju jače sjaji žarulja Ž1.
- B. I u paralelnome i u serijskome spoju jače sjaji žarulja Ž2.
- C. U paralelnome spoju jače sjaji žarulja Ž1, a u serijskome spoju jače sjaji žarulja Ž2.
- D. U paralelnome spoju jače sjaji žarulja Ž2, a u serijskome spoju jače sjaji žarulja Ž1.
Paralelni spoj
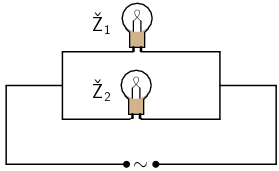
Napon na obje žarulje je jednak.
Serijski spoj
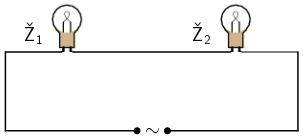
Kroz obje žarulje prolazi jednaka struja.
Jače će sjajiti ona žarulja na kojoj se razvija veća snaga.
Otpor žarulje Ž1:
\[P_{1}=U\,I=\frac{U^{2}}{R_{1}}\]
\[R_{1}=\frac{U^{2}}{P_{1}} \qquad(1)\]
Otpor žarulje Ž2:
\[P_{2}=U\,I=\frac{U^{2}}{R_{2}}\]
\[R_{2}=\frac{U^{2}}{P_{2}}\qquad(2)\]
Snaga žarulje Ž1 (100 W) veća je od snage žarulje Ž2 (40 W).
Iz izraza (1) i (2) zaključujemo da je otpor žarulje Ž2 veći od otpora žarulje Ž1:
\[R_{2} > R_{1}\]
U paralelnom spoju napon na žaruljama je jednak. Snaga na žaruljama je:
\[P=U\,I=U\,\frac{U}{R}\]
\[P=\frac{U^{2}}{R}\]
Otpor žarulje Ž1 je manji pa će se na njoj razviti veća snaga i ona će svjetliti većim sjajem.
U serijskom spoju kroz obje žarulje prolazi jednaka struja. Snaga na žaruljama je:
\[P=U\,I=I\,R\,I\]
\[P=I^{2}\,R\]
Otpor žarulje Ž2 je veći pa će se na njoj razviti veća snaga i ona će svjetliti većim sjajem.
Točan odgovor je C.
15. zadatak
Na slici je prikazan graf ovisnosti magnetskoga toka o vremenu u zavojnici.
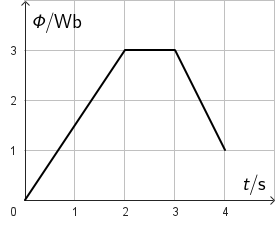
Koja slika točno prikazuje graf ovisnosti induciranoga napona o vremenu?
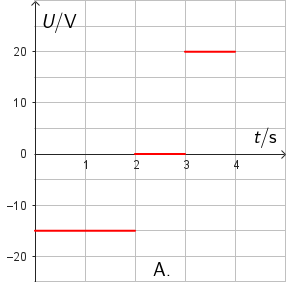
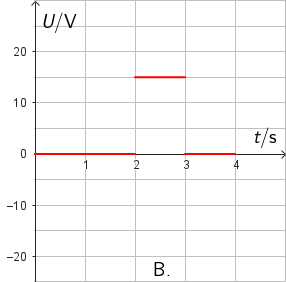
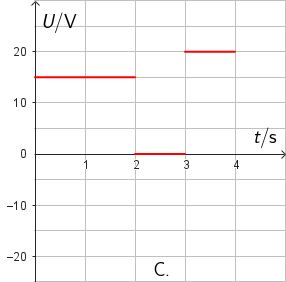
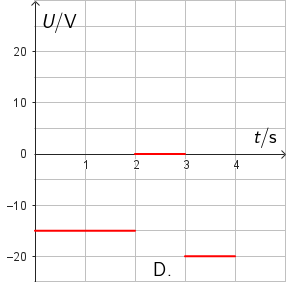
- A. graf A
- B. graf B
- C. graf C
- D. graf D
Primijenimo Faradayev zakon elektromagnetske indukcije na zavojnicu u promjenjivom magnetskom polju: \[U_{\textrm{i}}=-N\frac{\Delta \varPhi}{\Delta t}\] Promjenu magnetskog toka očitamo iz grafa kao nagib dijela pravca. N je broj zavoja koji nije poznat. Njega ćemo odrediti iz grafova koji su ponuđeni kao odgovor.

- 0. s do 2. s: \(\large\frac{\Delta \varPhi}{\Delta t}\normalsize =\large\frac{3}{2}\normalsize =\normalsize 1,5\,\textrm{V}\)
- 2. s do 3. s: \(\large\frac{\Delta \varPhi}{\Delta t}\normalsize =\normalsize 0\,\textrm{V}\)
- 3. s do 4. s: \(\large\frac{\Delta \varPhi}{\Delta t}\normalsize =\large\frac{-2}{1}\normalsize =\normalsize -2\,\textrm{V}\)
Usporedbom dobivenih induciranih napona s ponuđenim grafovima zaključujemo da zavojnica ima N = 10 zavoja
Inducirani naponi su, prema Faradayevom zakonu:
\[U_{\textrm{i}}=-N\frac{\Delta \varPhi}{\Delta t}\]
-15 V, 0 V i 20 V.
Točan odgovor je A.
16. zadatak
Tijelo mase m na opruzi napravi 40 titraja u jednoj minuti. Tijelo mase m zamijeni se tijelom mase
4 m.
Koliko titraja u jednoj minuti napravi tijelo 4 m?
- A. 10
- B. 20
- C. 80
- D. 160
Konstantu elastičnosti opruge prikažimo pomoću frekvencije titranja: \[k=m\,\omega^{2}\] \[\omega=2\,\pi\,f\] \[k=m\cdot 4\,\pi^{2}\cdot f^{2}\]
17. zadatak
Maksimalna kinetička energija matematičkoga njihala koje titra iznosi 0,5 mJ.
Koja je od navedenih tvrdnja za kinetičku energiju Ek i potencijalnu energiju
Ep njihala točna u nekome trenutku tijekom titranja njihala?
- A. Ek = 0 mJ i Ep = 0,25 mJ
- B. Ek = 0,25 mJ i Ep = 0 mJ
- C. Ek = 0,25 mJ i Ep = 0,25 mJ
- D. Ek = 0,5 mJ i Ep = 0,5 mJ
Ukupna energija harmonijskog oscilatora: \[E=E_{\textrm{k}}+E_{\textrm{p}}\] Elastična potencijalna energija: \[E_{\textrm{p}}=\frac{1}{2}\,k\,x^{2}\] U ravnotežnom položaju elongacija je jednaka nuli: \[x=0\] pa je i elastična potencijalna energija jednaka nuli: \[E_{\textrm{p}}=0\] Prema tome, u ravnotežnom položaju kinetička energija je maksimalna: \[E_{\textrm{k}}=\frac{1}{2}\,m\,v^{2}\] U ravnotežnom položaju ukupna energija harmonijskog oscilatora jednaka je kinetičkoj energiji: \[E=E_{\textrm{k}}+0\]
Ukupna energija harmonijskog oscilatora u ovom zadatku je: \[E=E_{\textrm{k}}=0,5\,\textrm{mJ}\] U ponuđenim odgovorima pronađimo onaj za kojeg vrijedi: \[E_{\textrm{k}}+E_{\textrm{p}}=0,5\,\textrm{mJ}\] Točan odgovor je C.
18. zadatak
Elektromagnetski val u vakuumu ima valnu duljinu 400 nm.
Kolika mu je valna duljina u sredstvu indeksa loma 2?
- A. 100 nm
- B. 200 nm
- C. 400 nm
- D. 800 nm
Kada val prelazi iz jednog sredstva u drugo, mijenja se njegova brzina, prema tome i njegova valna duljina, dok frekvencija ostaje ista.
Brzina elektromagnetskog vala u vakuumu: \[c=f\,\lambda_{0}\qquad (1)\] Brzina elektromagnetskog vala u sredstvu: \[v=f\,\lambda\qquad (2)\] Podijelimo jednadžbu (1) s jednadžbom (2): \[\frac{c}{v}=\frac{\lambda_{0}}{\lambda}\] Apsolutni indeks loma sredstva: \[n=\frac{c}{v}\] \[n=\frac{\lambda_{0}}{\lambda}\] \[\lambda=\frac{\lambda_{0}}{n}\] \[\lambda=\frac{400}{2}=200\,\textrm{nm}\]
19. zadatak
Na slikama je prikazana zraka svjetlosti koja iz zraka upada na komad stakla u obliku slova L.
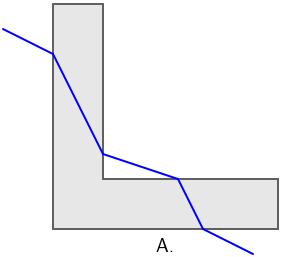
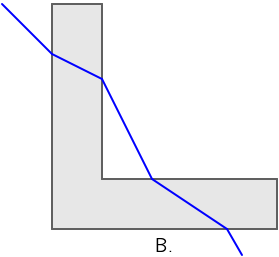
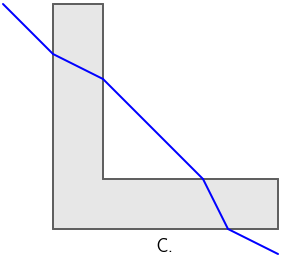
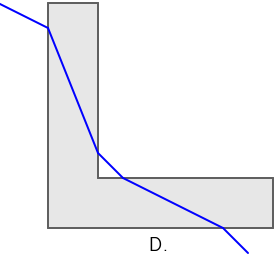
Koja od ponuđenih slika ispravno prikazuje mogući lom svjetlosti?
- A. slika A
- B. slika B
- C. slika C
- D. slika D
Indeks loma zraka je nz = 1,000293, a stakla
ns = 1,5.
Optičkom sredstvo s manjim indeksom loma nazivamo optički rjeđim, a sredstvo s većim indeksom loma optički gušćim sredstvom.
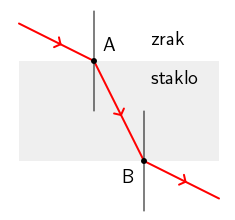
Zraka svjetlosti koja prelazi iz optički rjeđeg u optički gušće sredstvo (točka A na slici) lomi se prema okomici na granicu sredstava, dok se zraka svjetlosti
na prijelazu iz optički gušćeg u optički rjeđe sredstvo lomi od okomice (točka B na slici).
Iz slike također vidimo da je u točki A kut upadanja (kut između upadne zrake i okomice) veći od kuta loma (kut između lomljene zrake i okomice na granicu sredstava).
U točki B kut upadanja manji je od kuta loma.
Točan odgovor je slika C.
20. zadatak
Koje je vrste valova moguće polarizirati?
- A. samo valove zvuka
- B. samo transverzalne valove
- C. samo longitudinalne valove
- D. transverzalne i longitudinalne valove
Pomoć potražite na poveznici Polarizacija svjetlosti
Točan odgovor je B.
21. zadatak
Što treba učiniti s upadnim zračenjem kako bi se povećala maksimalna kinetička energija elektrona izbačenih fotoefektom iz metalne pločice?
- A. povećati intenzitet zračenja uz stalnu frekvenciju zračenja
- B. povećati valnu duljinu zračenja uz stalan intenzitet zračenja
- C. smanjiti frekvenciju zračenja uz stalan intenzitet zračenja
- D. smanjiti valnu duljinu zračenja uz stalan intenzitet zračenja
Kada foton padne na metal, ako pogodi elektron, predaje mu svoju energiju. Dio te energije pretvara se u rad za svladavanje energije vezanja W0 , a dio u kinetičku energiju fotoelektrona: \[E_{\textrm{f}}=W_{0}+E_{\textrm{k}}\]
Iz Einsteinove jednadžbe za fotoefekt: \[E_{\textrm{f}}=W_{0}+E_{\textrm{k}}\] odredimo maksimalnu kinetičku energiju izbačenih elektrona: \[E_{\textrm{k}}= E_{\textrm{f}}-W_{0}\] Frekvenciju upadnih fotona prikažimo pomoću brzine i valne duljine svjetlosti: \[f=\frac{c}{\lambda}\] Energija fotona koji upadaju na metal: \[E_{\textrm{f}}=h\,f=\frac{h\,c}{\lambda}\] Maksimalna kinetička energija izbačenih elektrona jednaka je: \[E_{\textrm{k}}= \frac{h\,c}{\lambda}-W_{0}\] Smanjenjem valne duljine upadnog elektromagnetskog zračenja povećat će se energija fotona (prvi član u jednadžbi), dok će izlazni rad ostati isti i zbog toga će se povećati i maksimalna kinetička energija izbačenih elektrona.
22. zadatak
Koliko neutrona ima izotop koji nastane β− raspadom izotopa 135Sn?
- A. 84
- B. 85
- C. 86
- D. 87
Neke nestabilne jezgre, koje imaju višak neutrona u odnosu na protone, mogu se spontano raspasti uz emisiju beta-minus čestica. Beta-minus čestice su brzi elektroni od kojih neki gotovo dostižu brzinu svjetlosti. Beta-minus emiteri su jezgre koje emitiraju beta-minus čestice. Beta-minus raspad prikazujemo jednadžbom: \[{_\textrm{Z}^\textrm{A}}\textrm{X}\rightarrow {_{\textrm{Z}+1}^{\,\,\,\,\,\textrm{A}}}\textrm{Y}+{_{\texttt{-}1}^{\,\,0}}\textrm{e}+\overline{\nu}\] Simbolički zapis jezgre atoma: \[_{Z}^{A}\,\textrm{X}\]
- \(\textrm{X}\) - simbolički znak jezgre atoma koji je jednak kemijskom simbolu atoma kojemu jezgra pripada.
- \(\textrm{Y}\) - jezgra nastala beta-minus raspadom.
- \(Z\) - protonski broj koji je jednak broju protona u jezgri. Odredimo ga iz periodnosg sustava kao redni broj atoma kojemu je X jezgra.
- \(A\) - nukleonski broj koji je jednak broju nukleona u jezgri. Nukleoni su protoni i neutroni.
- \({_{\texttt{-}1}^{\,\,0}}\textrm{e}\) - β− čestica (elektron).
- \(\overline{\nu}\) - antineutrino; \(Z=0\) i \(A=0\)
U periodnom sustavu pročitamo protonski broj za Sn (kositar): Z = 50.
Beta-minus raspad:
\[_{\;50}^{135\,}\textrm{Sn}\rightarrow _{Z}^{A}\textrm{X}+_{-1}^{\;\;0}\textrm{e}+\overline{\nu}\]
Pri radioaktivnom raspadu očuvani su protonski i nukleonski broj.
\[50=Z-1\Rightarrow Z=51\]
\[135=A+0\Rightarrow A=135\]
U zadatku se ne traži koja je jezgra Y, ali u periodnom sustavu pročitamo da je jezgra Y jezgra antimona.
\[_{\;50}^{135\,}\textrm{Sn}\rightarrow _{\,\,51}^{135}\textrm{Sb}+_{-1}^{\;\;0}\textrm{e}+\overline{\nu}\]
Jezgra koja je nastala ima Z = 51 proton i
A = 135 nukleona.
Broj neutrona je: N = A - Z = 135 - 51 = 84.
23. zadatak
Zašto prema Einsteinovoj teoriji relativnosti putovanje tijela brzinom svjetlosti nije moguće?
- A. jer bi ukupna energija tijela bila nula
- B. jer bi se masa mirovanja tijela približavala nuli
- C. jer bi ukupna energija tijela bila beskonačno velika
- D. jer bi vrijednost Lorentzova faktora bila jednaka nuli
Svaka čestica koja ima masu i svako tijelo imaju energiju koja je povezana s njihovom masom. To je najpoznatije Einsteinovo otkriće u specijalnoj teoriji relativnosti. \[E_{0}=mc^{2}\] Ova se energija zove energija mirovanja. To je ujedno i jedina energija ako tijelo miruje.
Ako se tijelo giba, osim energije mirovanja ima i kinetičku energiju pa mu je ukupna energija: \[E=E_{0}+E_{\textrm{k}}\] Ukupnu energiju prikazujemo kao: \[E=\frac{mc^{2}}{\sqrt{1-v^{2}/c^{2}}}\]
Ukupna energija tijela je:
\[E=\frac{mc^{2}}{\sqrt{1-v^{2}/c^{2}}}\]
Ako bi se tijelo gibalo brzinom svjetlosti, nazivnik bi bio jednak nuli i ukupna bi energija bila beskonačno velika, a to je apsurdno.
Točan odgovor je C.
24. zadatak
Koja je od navedenih tvrdnja za Sunce u dalekoj budućnosti točna?
- A. Sunce će postati crna rupa.
- B. Sunce će postati bijeli patuljak.
- C. Sunce će eksplodirati kao supernova.
- D. Sunce će postati neutronska zvijezda.
Sunce ima svoj životni vijek koji će jednom doći do kraja. Sunce se trenutno nalazi u srednjim godinama svog životnog ciklusa. Energija koju Sunce zrači u svim smjerovima nastaje fuzijom vodika u helij.
Za oko pet milijardi godina Sunce će potrošiti sav vodik u svojoj jezgri, a to znači početak njegovog kraja. Fuzija vodika u helij prestaje, Sunce se širi i postaje crveni div.
Nakon faze crvenog diva, Sunce odbacuje vanjske slojeve, a njegova se jezgra urušava u bijelog patuljka. Sunce će se ohladiti i postati
slabašna zvijezda.
Konačno, nakon što postane bijeli patuljak, Sunce polako gubi svu preostalu energiju i to će trajati nekoliko milijardi godina. Na kraju Sunce će postati hladno
i neprimjetno tijelo u svemiru.
Točan odgovor je B.
25. zadatak
Kolika je frekvencija okretanja kotača promjera 1,5 m ako točka na obodu kotača ima brzinu 72 km/h?
Odgovor:
Brzina točke na obodu kotača: \[v=\frac{2\,r\,\pi}{T}\] \[f=\frac{1}{T}\]
\[v=\frac{2\,r\,\pi}{T}\] \[v=2\,r\,\pi\frac{1}{T}=2\,r\,\pi\,f\] \[f=\frac{v}{2\,r\,\pi}\] \[f=4,24\,\textrm{Hz}\]
26. zadatak
Kolika je valna duljina protona koji se giba brzinom 0,01c?
Odgovor:
De Broglieva valna duljina: \[\lambda=\frac{h}{m\,v}\]
Masu protona pronađemo u knjižici formula: \[m=1,67\cdot 10^{-27}\,\textrm{kg}\] \[\lambda=\frac{h}{m\,v}=1,32·10^{-13}\,\textrm{m}\]
27. zadatak
Elektron se u vakuumu giba brzinom 3·104 m/s blizu ravnoga vodiča kojim prolazi struja
4 A.
Kolikom silom vodič djeluje na elektron u trenutku kad on prolijeće pokraj vodiča na udaljenosti 2,5 cm u smjeru
koji je paralelan s vodičem?
Odgovor:
Magnetsko polje dugog ravnog vodiča kroz kojega prolazi struja I na udaljenosti r od vodiča: \[B=\frac{\mu_{0}}{2\,\pi}\cdot \frac{I}{r}\] Sila kojom magnetsko polje djeluje na električni naboj koji se giba okomito na magnetsko polje: \[F=q\,v\,B\]
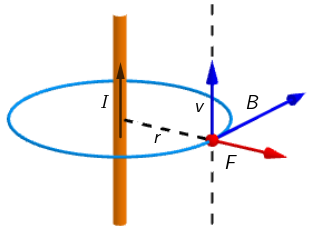
Elektron, na slici prikazan crvenom točkom, giba se paralelno s osi vodiča kroz koji prolazi struja. Vektor brzine elektrona okomit je na vektor
magnetskog polja. Sila kojom magnetsko polje djeluje na elektron prikazana je crveno obojenim vektorom koji je okomit na vektor brzine i na vektor
magnetskog polja:
\[F=e\,v\,B\]
\[B=\frac{\mu_{0}}{2\,\pi}\cdot \frac{I}{r}\]
\[F=\frac{\mu_{0}}{2\,\pi}\cdot \frac{e\,v\,I}{r}\]
\[F=1,54\cdot 10^{−19}\, \textrm{N}\]
28. zadatak
Električna peć priključena na gradsku mrežu ima 2 metra dugu grijaću žicu te za 25 minuta povisi
temperaturu u prostoriji za 5 oC.
Kolika bi trebala biti duljina grijaće žice od istoga materijala jednakoga poprečnog presjeka kako bi se za 15 minuta postiglo jednako
povećanje temperature u toj prostoriji? Gubitci topline iz prostorije u okolinu i promjena poprečnoga presjeka žice su zanemarivi.
Odgovor:
Toplina koju oslobađa grijača žica ijednaka je radu električne struje koja prolazi žicom: \[W = U\,I\,\Delta t\] Ohmov zakon: \[I=\frac{U}{R}\] \[W=\frac{U^{2}}{R}\,\Delta t\]
29. zadatak
U medicinskoj dijagnostici koristi se izotop fluora F-18 čije je vrijeme poluraspada 110 minuta.
Aktivnost je unesenoga fluora u organizam 370 MBq.
Koliko je jezgri izotopa F-18 prisutno u krvotoku pacijenta nakon jednoga sata?
Odgovor:
Ako neki radioaktivni uzorak u početnom trenutku sadrži N0 jezgara, tijekom vremena taj će se broj smanjivati. Nakon vremena T1/2, preostat će N0 /2 jezgara, nakon još jednog vremena poluraspada preostat će ih N0 /4 itd. Broj neraspadnutih jezgara N smanjuje se eksponencijalno tijekom vremena t: \[N=N_{0}\,e^{\large{\mathbf{−}λ\,t}}\] T1/2 je vrijeme poluraspada. To je vrijeme nakon kojega se raspadne polovina početnog broja jezgara. Konstanta λ zove se konstanta radioaktivnog raspada: \[\lambda=\frac{\textrm{ln}\,2}{T_{1/2}}\] Zakon radioaktivnog raspada može se prikazati i u obliku: \[N=N_{0}\cdot 2^{\mathbf{-}\large{\frac{t}{T_{1/2}}}}\]
Aktivnost je jednaka broju raspada u sekundi i označuje se sa A: \[A=\lambda\,N\Rightarrow N=\frac{A}{\lambda}\]
Odredimo konstantu radioaktivnog raspada: \[\lambda=\frac{\textrm{ln}\,2}{T_{1/2}}=\frac{\textrm{ln}\,2}{110\cdot 60}=1,050223\cdot 10^{−4}\,\frac{1}{\textrm{s}}\] Iz početne aktivnosti, koja je zadana, odredimo početni broj jezgri: \[N_{0}=\frac{A_{0}}{\lambda}=\frac{370\cdot 10^{6}}{1,050223\cdot 10^{−4}}=3,52306129\cdot 10^{12}\] Iz zakona radioaktivnog raspada odredimo broj jezgri nakon jednog sata: \[N=N_{0}\cdot 2^{\mathbf{-}\large{\frac{t}{T_{1/2}}}}=2,41\cdot 10^{12}\]
30. zadatak
Učenici su dobili zadatak odrediti žarišnu daljinu sabirne leće uz pomoć slike predmeta dobivene na zastoru.
30.1. Koja je od navedenih tvrdnja točna za sliku predmeta dobivenu na zastoru?
- Slika je uspravna, virtualna i uvećana.
- Slika je uspravna, realna i uvećana.
- Slika je obrnuta, virtualna i uvećana.
- Slika je obrnuta, realna i uvećana.
Redni broj tvrdnje:
30.2. Od mjerenja zapisanih u tablici samo je jedno ispravno.
Odaberite ispravno mjerenje:
| \(\,\textrm{#}\,\) | \(a/\textrm{cm}\) | \(b/\textrm{cm}\) | \(y/\textrm{cm}\) | \(y^{'}/\textrm{cm}\) |
|---|---|---|---|---|
| 1. | 10,00 | -5,05 | 0,60 | 0,30 |
| 2. | 8,20 | 12,40 | 3,50 | 2,30 |
| 3. | 15,30 | -30,80 | 5,30 | -10,20 |
| 4. | 12,40 | 6,50 | 6,10 | -3,20 |
| 5. | -13,30 | 7,65 | 2,80 | 1,60 |
Ispravno mjerenje:
30.3. Kolika je žarišna daljina leće?
f =
30.1.
Konvergentna leća može dati sliku koja je:
- realna i obrnuta, a može biti, ovisno o položaju predmeta u odnosu na žarište, umanjena, jednako velika kao predmet ili uvećana
- virtualna, uspravna i uvećana
Točan odgovor: 4.
(Odgovor 1. nije točan jer virtualnu sliku nije moguće dobiti na zastoru.)
30.2.
Jednadžba leće:
\[\frac{1}{a}+\frac{1}{b}=\frac{1}{f}\]
Za realne predmete i slike a i b su pozitivni, a za virtualne negativni.
Linearno povećanje leće:
\[m=\frac{y'}{y}\]
ili
\[m=\frac{-b}{a}\]
Slika je realna jer je dobivena na zastoru. Podaci u 1. i 3. retku nisu mogući jer je b < 0.
Podaci u 5. retku nisu mogući jer je a < 0.
Podaci u 2. retku nisu mogući jer je y' < 0, a realna slika ne može biti uspravna.
Prema tome, točni su podaci u 4. retku.
30.3.
\[\frac{1}{f}=\frac{1}{a}+\frac{1}{b}\Rightarrow f=4,26\, \textrm{cm}\]
31. zadatak
Tijelo A mase 3 kg povezano je nerastezljivom niti zanemarive mase s tijelom B mase 5 kg.
Tijela miruju na horizontalnoj podlozi. Koeficijenti trenja između pojedinoga tijela i podloge su jednaki i iznose 0,1. U prvome slučaju na tijelo A
djeluje horizontalna vučna sila iznosa 25 N. U drugome slučaju na tijelo B djeluje horizontalna vučna sila istoga iznosa,
no suprotne orijentacije.
Kolika je razlika iznosa napetosti niti između tijela u prvome i drugome slučaju?
Odgovor:
Odredite sve sile koje djeluju na tijelo A i na tijelo B i zatim primijenite drugi Newtonov zakon.
1. Vučna sila djeluje na tijelo A
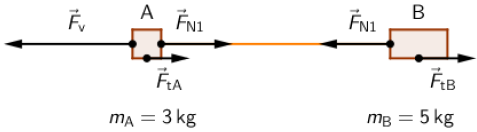
Jednadžbe gibanja tijela A i tijela B: \[F_{\large{\textrm{v}}}-F_{\textrm{N1}}-F_{\textrm{tA}}=m_{\textrm{A}}\cdot a\qquad (1)\] \[F_{\textrm{N1}}-F_{\textrm{tB}}=m_{\textrm{B}}\cdot a\qquad(2)\] Iz jednadžbe (2) odredimo akceleraciju i uvrstimo u jednadžbu (1): \[a=\frac{F_{\textrm{N1}}-F_{\textrm{tB}}}{m_{\textrm{B}}}\] \[F_{\large{\textrm{v}}}-F_{\textrm{N1}}-F_{\textrm{tA}}=m_{\textrm{A}}\cdot \frac{F_{\textrm{N1}}-F_{\textrm{tB}}}{m_{\textrm{B}}}\] \[F_{\textrm{N1}}\left(m_{\textrm{A}}+m_{\textrm{B}}\right)=m_{\textrm{B}}\cdot F_{\large{\textrm{v}}}-\mu\cdot m_{\textrm{A}}\cdot m_{\textrm{B}}\cdot g + \mu\cdot m_{\textrm{A}}\cdot m_{\textrm{B}}\cdot g\] \[F_{\textrm{N1}}=\frac{m_{\textrm{B}}\cdot F_{\large{\textrm{v}}}}{m_{\textrm{A}}+m_{\textrm{B}}}\qquad (3)\]
2. Vučna sila djeluje na tijelo B

Mogli bismo ponoviti postupak kao u slučaju 1., ali to nije potrebno jer je zadatak simetričan. Dovoljno je u izrazu (3) zamijeniti \(m_{\textrm{B}}\) s m_{\textrm{A}} i obrnuto. \[F_{\textrm{N2}}=\frac{m_{\textrm{A}}\cdot F_{\large{\textrm{v}}}}{m_{\textrm{A}}+m_{\textrm{B}}}\qquad (4)\] \[\Delta F_\textrm{N}=F_\textrm{N1}-F_\textrm{N2}=\frac{m_\textrm{B}\cdot F_{\large\textrm{v}}}{m_\textrm{A}+m_\textrm{B}}-\frac{m_\textrm{A}\cdot F_{\large\textrm{v}}}{m_\textrm{A}+m_\textrm{B}}\] \[\Delta F_\textrm{N}=\frac{F_{\large{\textrm{v}}}\left(m_\textrm{B}-m_\textrm{A}\right)}{m_{\textrm{A}}+m_{\textrm{B}}}=\frac{50}{8}=6,25\,\textrm{N}\]
32. zadatak
Na horizontalnu cijev promjera 4 cm spojena je druga horizontalna cijev promjera 2 cm iz koje istječe voda
u bačvu volumena 50 litara . Razlika je statičkih tlakova vode u tim dvjema cijevima 500 Pa.
Koliko je vremena potrebno kako bi se u potpunosti napunila prazna bačva u koju utječe voda iz cijevi?
Hidrostatski tlak u cijevi je zanemariv. Gustoća vode iznosi 1000 kg/m3.
Odgovor:
Primijenite Bernoullijevu jednadžbu, jednadžbu kontinuiteta i protok vode.
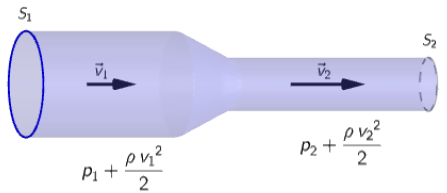
Bernoullijeva jednadžba: \[p_{\large{_1}}+\frac{\rho\,{v_{1}}^{2}}{2}=p_{\large{_2}}+\frac{\rho\,{v_{2}}^{2}}{2}\] \[p_{\large{_1}}-p_{\large{_2}}=\frac{\rho}{2}\,\left({v_{2}}^{2}-{v_{1}}^{2}\right)\] Jednadžba kontinuiteta: \[v_{1}\,S_{1}=v_{2}\,S_{2}\] \[v_{1}=\frac{S_{2}}{S_{1}}\,v_{2}\] \[\Delta p=p_{\large{_1}}-p_{\large{_2}}\] \[\Delta p=\frac{\rho}{2}\,\left(v_{2}^{\;2}-\frac{S_{2}^{\,2}}{S_{1}^{\;2}}\,v_{2}^{\;2}\right)\] \[\Delta p=\frac{\rho\,v_{2}^{\;2}}{2}\left(1-\left(\frac{S_{2}}{S_{1}}\right)^{2}\right)\] \[\Delta p=\frac{\rho\,v_{2}^{\;2}}{2}\left(1-\left(\frac{r_{2}^{\;2}\,\pi}{r_{1}^{\;2}\,\pi}\right)^{2}\right)\] \[\Delta p=\frac{\rho\,v_{2}^{\;2}}{2}\left(1-\frac{1}{16}\right)\] \[\Delta p=\frac{\rho\,v_{2}^{\;2}}{2}\cdot \frac{15}{16}\] \[v_{2}^{\;2}=\frac{2\cdot 16\cdot \Delta p}{15\cdot p}=\frac{2\cdot 16\cdot 500}{15\cdot 1000}\] \[v_{\large{_2}}=\sqrt{\frac{16}{15}}=1,03\,\frac{\textrm{m}}{\textrm{s}}\] Protok vode: \[Q=\frac{\Delta V}{\Delta t}=S_{2}\,v_{\large{_2}}\] \[S_{2}=r_{2}^{\;2}\,\pi=10^{-4}\,\pi\, \textrm{m}^{2}\] \[\Delta t=\frac{\Delta V}{S_{2}\,v_{\large{_2}}}=\frac{50\cdot 10^{-3}}{10^{-4}\,\pi\cdot 1,03}=154,1\,\textrm{s}\]
33. zadatak
Na slici je prikazan kružni proces kroz koji prolazi jedan mol idealnoga jednoatomnog plina. Proces se sastoji od triju izobara i triju izohora.
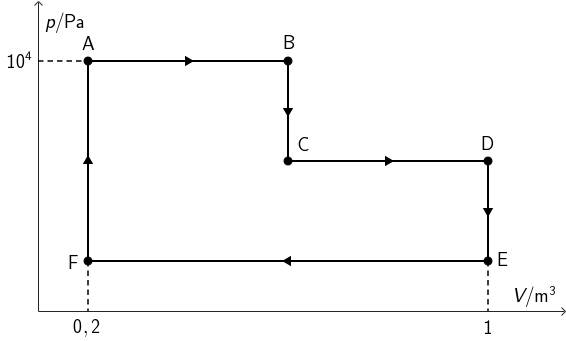
Od stanja A do stanja B plin izvrši rad iznosa 4 kJ, što je duplo više rada nego što izvrši od stanja B do stanja E.
Kolika je unutarnja energija plina u točki C?
Odgovor:
Rad plina pri izobarnom procesu:
\[W=p\,\Delta V\]
Pomoću p, V grafa rad određujemo kao površinu ispod izobare, sve do osi V.
Rad plina pri izohornom procesu jednak je nuli jer se volumen plina ne mijenja.
Unutarnja energija jednoatomnog idealnog plina:
\(U=\frac{\large{3}}{\large{2}}\,N\,k\,T\) ili \(U=\frac{\large{3}}{\large{2}}\,p\,V\)
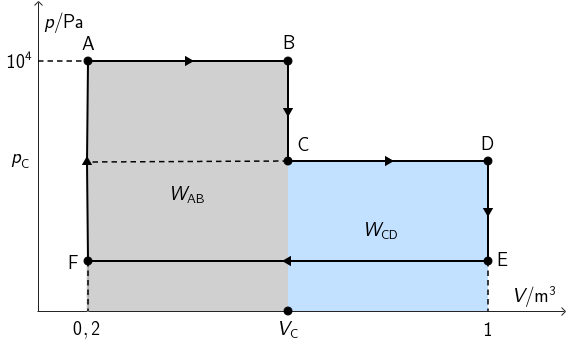
Podaci poznati iz zadatka: \[W_{\textrm{AB}}=4\,\textrm{kJ}\] \[W_{\textrm{CD}}=2\,\textrm{kJ}\] Podaci vidljivi iz grafa: \[p_\textrm{A}=10^{4}\,\textrm{Pa}\] \[V_\textrm{D}=1\,\textrm{m}^{3}\] \[V_\textrm{C}=_\textrm{B}\] Rad pri izohornim procesima jednak je nuli.
Rad pri izobarnom procesu AB jednak je površini sivo obojenog pravokutnika: \[W_{\textrm{AB}}=p_\textrm{A}\cdot \left(V_\textrm{B}-V_\textrm{A}\right)\] \[V_\textrm{B}=\frac{W_\textrm{AB}}{p_{\textrm{A}}}+V_{\textrm{A}}=0,6\,\textrm{m}^{3}\] Iz grafa je vidljivo da je to i volumen plina u stanju C: \[V_\textrm{C}=0,6\,\textrm{m}^{3}\] Rad pri izobarnom procesu CD jednak je površini plavo obojenog pravokutnika: \[W_\textrm{CD}=p_\textrm{C}\cdot \left(V_\textrm{D}-V_\textrm{C}\right)\] \[p_\textrm{C}=\frac{W_\textrm{CD}}{V_\textrm{D}-V_\textrm{C}}=5000\,\textrm{Pa}\] U modelu idealnog plina zanemarujemo potencijalnu energiju molekula pa je unutarnja energija jednoatomnog idealnog plina jednaka srednjoj kinetičkoj energiji svih molekula: \[U=N\,\overline{E}_\textrm{k}=N\cdot \frac{3}{2}\,k\,T=\frac{3}{2}\,N\,k\,T\] Usporedbom s jednadžbom stanja idealnog plina: \[p\,V=N\,k\,T\] zaključujemo da unutarnju energiju idealnog plina možemo odrediti i kao: \[U=\frac{3}{2}\,p\,V\] Unutarnja energija u stanju koje odgovara točki C jednaka je: \[U_\textrm{C}=\frac{3}{2}\,p_\textrm{C}\,V_\textrm{C}\] \[U_\textrm{C}=4500\, \textrm{J}=4,5\,\textrm{kJ}\]
34. zadatak
Nabijena čestica mase 3,32·10-27 kg i naboja q ubrzava se iz mirovanja razlikom potencijala
4,9·104 V i tako ubrzana ulijeće okomito na silnice homogenoga magnetskog polja 1,5 T.
Čestica u polju opisuje kružnicu polumjera 0,03 m.
Koliko iznosi naboj čestice?
Odgovor:
Rad električnog polja: \[W=q\,U\] jednak je promjeni kinetičke enegije naboja q: \[W=E_\textrm{k,kon}-E_\textrm{k,poc}\] Na nabijenu česticu u okomitom smjeru djeluje Lorentzova sila: \[F_\textrm{L}=q\,v\,B\] Lorentzova sila ima ulogu centripetalne sile: \[F_\textrm{L}=F_\textrm{C}\]
Električno polje obavlja rad koji je jednak promjeni kinetičke energije nabijene čestice. Naboj u početku miruje pa ke početna kinetička energija jednak 0: \[W=\frac{m\,v^{2}}{2}-0\] \[W=q\,U\] \[q\,U=\frac{m\,v^{2}}{2}\] Nabijena čestica ulijeće okomito na magnetsko polje pa je Lorentzova sila: \[F_\textrm{L}=q\,v\,B\] U svakoj točki putanje Lorentzova sila je okomita na vektor brzine čestice, što znači da je je putanja kružnica, a Lorentzova sila ima ulogu centripetalne sile: \[q\,v\,B=\frac{m\,v^{2}}{r}\] \[q\,B=\frac{m\,v}{r}=\frac{p}{r}\] \[q=\frac{p}{B\,r}\Rightarrow p=q\,B\,r\qquad(1)\] U jednadžni: \[q\,U=\frac{m\,v^{2}}{2}\] razlomak proširimo s m: \[q\,U=\frac{m^{2}\,v^{2}}{2\,m}=\frac{p^{2}}{2\,m}\] \[p^{2}=2\,m\,q\,U\] U ovu jednadžbu uvrstimo p iz izraza (1): \[q^{2}\,B^{2}\,r^{2}=2\,m\,q\,U\] \[q=\frac{2\,m\,U}{B^{2}\,r^{2}}\] \[q=1,61\cdot 10^{-19}\,\textrm{C}\]
35. zadatak
Osoba sluša glazbu koja dolazi iz točkastoga izvora zvuka snage 2,5 mW. Izvor je smješten tako da je osobi jedno uho od njega udaljeno 55 cm,
a drugo 57 cm.
Kolika je razlika razina zvukova koje osoba čuje lijevim i desnim uhom?
Odgovor:
Razina intenziteta zvuka: \[L=10\,\textrm{log}\,\frac{I}{I_{0}}\] Intenzitet zvuka: \[I=\frac{P}{S}=\frac{P}{4\,r^{2}\pi}\] Prag čujnosti: \[I_{0}=10^{-12}\,\textrm{W/m}^{2}\]
Razlika razina intenziteta zvuka za oba uha: \[\Delta L=L_{1}-L_{2}=10\,\textrm{log}\,\frac{I_{1}}{I_{0}}-10\,\textrm{log}\,\frac{I_{2}}{I_{0}}\] \[\Delta L=10\,\textrm{log}\,I_{1}-10\,\textrm{log}\,I_{0}-10\,\textrm{log}\,I_{2}+10\,\textrm{log}\,I_{0}\] \[\Delta L=10\,\textrm{log}\,I_{1}-10\,\textrm{log}\,I_{2}=10\left(\textrm{log}\,I_{1}-\textrm{log}\,I_{2}\right)\] \[\Delta L=10\,\textrm{log}\,\frac{I_{1}}{I_{2}}=10\,\textrm{log}\,\left(\frac{P}{4\,r_{1}^{\;2\,}\pi}\cdot \frac {4\,r_{2}^{\;2\,}\pi}{P}\right)\] \[\Delta L=10\,\textrm{log}\,\frac{r_{2}^{\;2}}{r_{1}^{\;2}}=10\,\textrm{log}\,\frac{57^{2}}{55^{2}}\] \[\Delta L=0,31\,\textrm{dB}\]