Ljetni rok 2016. godine
1. zadatak
Dva tijela jednakih masa gibaju se po kružnim putanjama polumjera \(r_{1}\) i \(r_{2}\) jednakim kutnim brzinama.
Koja je od navedenih veličina jednaka za ta dva tijela?
- A. centripetalna sila
- B. obodna brzina
- C. centripetalno ubrzanje
- D. frekvencija
Kutnu brzinu \(\omega\) možemo prikazati kao: \[\omega=\frac{2\pi}{T}\] gdje je \(T\) ophodno vrijeme (vrijeme potrebno tijelu da jednom obiđe kružnicu).
Oba tijela kruže jednakim kutnim brzinama: \[ \begin{matrix} \begin{align*} &\omega_{1}=\omega_{2}\\ &\frac{2\,\pi}{T_{1}}=\frac{2\,\pi}{T_{2}}\\ &T_{1}=T_{2}\\ \end{align*} \end{matrix} \] Frekvencija gibanja tijela po kružnici je: \[f=\frac{1}{T}\] pa zaključujemo: \[f_{1}=f_{2}\]
2. zadatak
Dva tijela različitih masa, \(M > m\), povezana su nerastezljivom niti i ovješena preko nepomične koloture kao što je prikazano na slici.
Koji izraz opisuje ubrzanje tijela mase \(M\)?
Masa koloture te trenje između koloture i niti su zanemarivi.
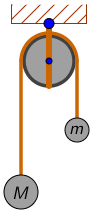
- A. \(a=M\,g/m\)
- B. \(a=(M-m)\,g/(M+m)\)
- C. \(a=g\)
- D. \(a=M\,m\,g/(M+m)\)
Sile koje djeluju na oba tijela prikazane su na crtežu.
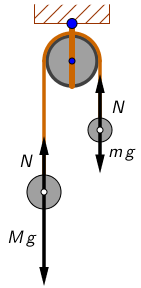
Akceleracije oba tijela jednake su po iznosu jer su tijela privezana nerastezljivom niti. Primijenimo na oba tijela temeljni zakon gibanja: \[ \begin{matrix} \begin{align*} &Mg-N=Ma\\ &N-mg=ma \end{align*} \end{matrix} \] Zbrojimo jednadžbe: \[Mg-N+N-mg=Ma+ma\] Nakon sređivanja dobijemo: \[(M-m)g=(M+m)a\] Akceleracija kojom se giba tijelo mase \(M\) iznosi: \[a=\frac{M-m}{M+m}\cdot g\]
3. zadatak
Tijelo mase \(0,1\,\textrm{kg}\) bačeno je s visine \(2,5\,\textrm{m}\) početnom brzinom \(10\,\textrm{m/s}\) prema dolje.
Kolika je kinetička energija tijela na visini \(1\,\textrm{m}\) iznad tla?
Otpor i uzgon u zraku su zanemarivi.
- A. \(1,0\,\textrm{J}\)
- B. \(6,0\,\textrm{J}\)
- C. \(6,5\,\textrm{J}\)
- D. \(7,5\,\textrm{J}\)
Početna mehanička energija tijela u trenutku bacanja jednaka je zbroju njegove kinetičke i gravitacijske potencijalne energije: \[E_{1}=\frac{mv^{2}}{2}+mgh\] Napišite izraz za ukupnu mehaničku energiju na visini \(1\,m\) iznad tla i primijenite zakon očuvanja mehaničke energije.
Mehanička energija tijela u trenutku bacanja jednaka je: \[E_{1}=\frac{mv^{2}}{2}+mgh\] Nakon uvrštavanja podataka i računanja dobijemo: \[E_{1}=7,5\,\textrm{J}\] Mehanička energija tijela na visini \(1\,m\) iznad tla jednaka je: \[E_{2}=E_{k}+mgh_{2}\] Na osnovu zakona očuvanja mehaničke energije zaključujemo: \[E_{2}=E_{1}\] Prema tome, kinetička energija tijela na visini \(1\,\textrm{m}\) iznosi: \[E_{k}=E_{2}-mgh_{2}=6,5\,\textrm{J}\]
4. zadatak
S visine \(25\,\textrm{m}\) izbačeno je tijelo u vodoravnome smjeru početnom brzinom \(20\,\textrm{m/s}\).
Koliki je iznos brzine tijela pri udaru o tlo?
Otpor i uzgon u zraku su zanemarivi.
- A. \(20\,\textrm{m/s}\)
- B. \(22,8\,\textrm{m/s}\)
- C. \(30\,\textrm{m/s}\)
- D. \(53,6\,\textrm{m/s}\)
Brzinu tijela koje je izbačeno u horizontalnom smjeru u bilo kojem trenutku možemo odrediti iz izraza: \[v=\sqrt{v_{x}^{2}+v_{y}^{2}}\] Komponenta brzine u smjeru osi \(x\) jednaka je početnoj brzini, a komponenta brzine u smjeru osi \(y\) jednaka je brzini slobodnog pada.
U izraz za brzinu \[v=\sqrt{v_{x}^{2}+v_{y}^{2}}\] uvrstimo \(v_{x}=v_{0}\) i \(v_{y}=\sqrt{2gh}\) : \[v=\sqrt{v_{0}^{2}+2gh}=30\,\textrm{m/s}\]
5. zadatak
Ubrzanje sile teže na površini Zemlje polumjera \(R\) i mase \(M\) iznosi \(g\).
Na kojoj visini h iznad površine Zemlje ubrzanje tijela iznosi \(g/16\) ?
- A. \(R/4\)
- B. \(3\,R\)
- C. \(4\,R\)
- D. \(16\,R\)
Akceleracija sile teže na udaljenosti \(r\) od središta Zemlje iznosi: \[g=G\frac{M}{r^{2}}\]
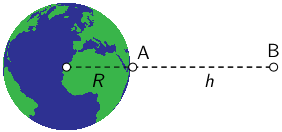
Akceleracija sile teže u točki A na površini Zemlje iznosi: \[g=G\frac{M}{R^{2}}\] Akceleracija sile teže u točki B na visini \(h\) iznad površine Zemlje iznosi: \[g_{h}=G\frac{M}{(R+h)^{2}}\] Iz \[g_{h}=\frac{g}{16}\] slijedi \[R+h=4\cdot R\] Rezultat je: \[h=3R\]
6. zadatak
Plin se nalazi u posudi stalnoga volumena na temperaturi \(T\) i tlaku \(p\).
Kolika će biti temperatura plina pri tlaku \(\sqrt{3}\,p\)?
- A. \(T/3\)
- B. \(\sqrt{3}\,T/3\)
- C. \(\sqrt{3}\,T\)
- D. \(3\,T\)
Za izohorni proces vrijedi: \[\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\]
Iz: \[\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\] dobijemo: \[ \begin{matrix} \begin{align*} &T_{2}=\frac{P_{2}}{P_{1}}\,T_{1}\\ &T_{2}=\frac{\sqrt{3}\,P}{P}\,T\\ &T_{2}=\sqrt{3}\, T \end{align*} \end{matrix} \]
7. zadatak
Koja je od navedenih tvrdnja karakteristična za Brownovo gibanje?
- A. Sudari molekula su savršeno elastični.
- B. Molekule imaju određene dimenzije.
- C. Između molekula djeluju odbojne sile.
- D. Molekule se nasumično gibaju.
Ako na površinu vode stavimo cvjetni prah, pojedine čestice će se gibati nasumično. Zašto?
Brownovo gibanje neposredni je dokaz nasumičnog gibanja molekula. Molekule vode udaraju o čestice cvjetnog praha u svim smjerovima, zbog čega je njihovo gibanje nasumično. Brownovo gibanje može se opaziti samo kod čestica promjera od \(10^{-7}\,\textrm{m}\) do \(10^{-6}\,\textrm{m}\).
8. zadatak
Graf prikazuje ovisnost temperature \(T\) o količini topline \(Q\) koja se oduzima određenoj masi vode. Voda se početno nalazi u plinovitome stanju, a zatim se hladi odvođenjem topline.
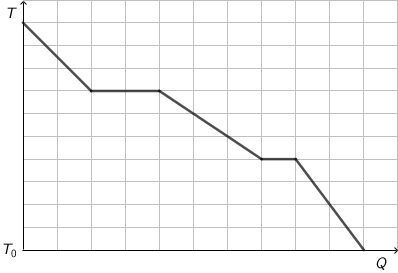
Tijekom kojega je od navedenih procesa odvedena najmanja količina topline?
- A. tijekom snižavanja temperature plina
- B. tijekom kristalizacije (očvršćivanja)
- C. tijekom snižavanja temperature tekućine
- D. tijekom kondenzacije
Iz grafa odredite toplinu koja se oduzima pri hlađenju vodene pare, kondenzaciji vodene pare u vodu, hlađenju vode, očvršćivanju vode u led i hlađenju leda. Koja od tih toplina je najmanja?
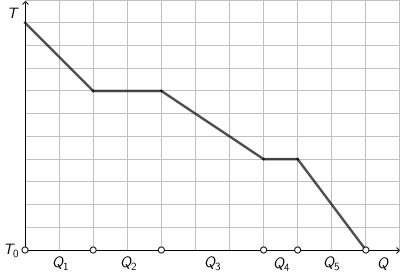
Iz grafa je vidljivo da je najmanja toplina \(Q_{4}\) oduzeta pri očvršćivanju vode u led.
9. zadatak
Električki neutralnomu tijelu dovedeno je \(10^{5}\) elektrona.
Koliko iznosi količina naboja toga tijela?
- A. \(-1,6\cdot 10^{-24}\,\textrm{C}\)
- B. \(-1,6\cdot 10^{-14}\,\textrm{C}\)
- C. \(1,6\cdot 10^{-24}\,\textrm{C}\)
- D. \(1,6\cdot 10^{-14}\,\textrm{C}\)
Ukupan naboj nekog tijela može se prikazati kao \(q=n\,e\).
\begin{matrix} \begin{align*} &n=10^{5}\\ &e=-1,6\cdot 10^{-19}\\ &q=n\cdot e\\ &q=-1,6\cdot 10^{-14}\,\textrm{C} \end{align*} \end{matrix}
10. zadatak
Za koju je fizikalnu veličinu mjerna jedinica \(\textrm{A}\textrm{h}\) (ampersat)?
- A. za električnu struju
- B. za električnu silu
- C. za rad električne sile
- D. za električni naboj
Kako je definirana električna struja?
Iz definicije električne struje: \[I=\frac{q}{t}\] vidimo da je: \[[q]=[I]\cdot[t]\] Amper je mjerna jedinica za struju, a sat za vrijeme.
11. zadatak
Dva trošila različitih otpora spojena su serijski na izvor istosmjernoga napona.
Koja je od navedenih tvrdnja točna za taj strujni krug?
- A. Napon je jednak na obama trošilima.
- B. Napon je najmanji na trošilu najvećega otpora.
- C. Struja je najmanja kroz trošilo najvećega otpora.
- D. Struja je jednaka kroz oba trošila.
Na paralelno spojenim trošilima jednak je napon. Što vrijedi za serijski spojena trošila?
Kroz serijski spojena trošila prolazi jednaka struja.
12. zadatak
Kroz dva duga ravna vodiča koji se sijeku pod pravim kutom prolaze struje \(I_{1} = I_{2} = 10\, \textrm{A}\).
Točka A udaljena je \(2 \textrm{cm}\) od svakoga vodiča kao što je prikazano na slici.
Koliki je iznos magnetskoga polja \(B\) u točki A ?
Vodiči i točka A nalaze se u istoj ravnini.
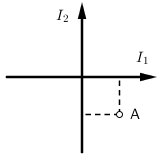
- A. \(0\,\textrm{T}\)
- B. \(5\cdot 10^{-5}\,\textrm{T}\)
- C. \(1\cdot 10^{-4}\,\textrm{T}\)
- D. \(2\cdot 10^{-4}\,\textrm{T}\)
Magnetsko polje u točki koja se nalazi na udaljenosti \(r\) od dugog ravnog vodiča kojim prolazi struja \(I\) iznosi: \[B=\frac{\mu_{0}}{2\pi}\frac{I}{r}\] Smjer i orijentaciju magnetskog polja odredimo pravilom desne ruke.
Kroz oba vodiča prolazi jednaka struja. U točki A koja je jednako udaljena od oba vodiča iznosi magnetskog polja oba vodiča bit će jednaki: \[B_{1}=B_{2}=\frac{\mu_{0}}{2\pi}\frac{I}{r}\] Uvrstimo podatke: \[B_{1}=B_{2}=\frac{4\pi\cdot 10^{-7}}{2\pi}\frac{10}{2\cdot 10^{-2}}=10^{-4}\,\textrm{T}\] Primjenom pravila desne ruke zaključujemo da oba magnetska polja imaju smjer u ravninu crtanja i jednaku orijentaciju. Rezultantno magnetsko polje jednako je: \[B=B_{1}+B_{2}=2\cdot 10^{-4}\,\textrm{T}\]
13. zadatak
Kondenzator kapacitivnoga otpora \(120\,\Omega\) nalazi se u krugu izmjenične struje frekvencije \(60\,\textrm{Hz}\).
Koliki je kapacitet toga kondenzatora?
- A. \(22,1\,\mu\textrm{F}\)
- B. \(138,9\,\mu\textrm{F}\)
- C. \(0,318\,\textrm{F}\)
- D. \(2\,\textrm{F}\)
Kapacitivni otpor jednak je: \[R_{C}=\frac{1}{C\,\omega}\]
\begin{matrix} \begin{align*} &R_{C}=\frac{1}{C\,\omega}\\ &C=\frac{1}{R_{C}\,\omega}\\ &\omega=2\pi f\\ &R_{C}=22,1\,\mu\textrm{F} \end{align*} \end{matrix}
14. zadatak
Što je amplituda?
- A. bilo koja udaljenost od ravnotežnoga položaja
- B. najveća udaljenost od ravnotežnoga položaja
- C. broj titranja u jedinici vremena
- D. vrijeme potrebno za jedan titraj
Elongacija titranja je udaljenost tijela koje titra od ravnotežnog položaja. Kako nazivamo maksimalnu elongaciju?
Amplituda titranja je najveća udaljenost tijela koje titra od ravnotežnog položaja.
15. zadatak
Valna duljina elektromagnetskoga vala približno je jednaka promjeru jabuke.
Kojemu dijelu elektromagnetskoga spektra pripada taj val?
- A. mikrovalovima
- B. ultraljubičastomu dijelu spektra
- C. vidljivoj svjetlosti
- D. infracrvenomu dijelu spektra
Pomoć potražite na poveznici Elektromagnetski spektar.
Točan odgovor je A. - mikrovalovi
16. zadatak
Dva ravna zrcala Z1 i Z2
međusobno zatvaraju kut α. Zraka svjetlosti dolazi paralelno sa zrcalom Z2.
Koja slika prikazuje pravilnu putanju zrake nakon refleksije na zrcalima?
Napomena: Pod A. i C. leća je konvergentna, a pod B. i D. divergentna.)
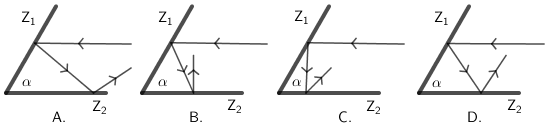
- A. Slika A.
- B. Slika B.
- C. Slika C.
- D. Slika D.
Primijenite zakon refleksije svjetlosti.
Prema zakonu refleksije svjetlosti kut upadanja jednak je kutu odbijanja. Točan odgovor je D.
17. zadatak
Koji od navedenih valova ne mogu biti polarizirani?
- A. valovi zvuka
- B. radiovalovi
- C. mikrovalovi
- D. valovi svjetlosti
Pri širenju transverzalnih valova čestice sredstva titraju okomito na smjer širenja vala. Takvi valovi mogu biti polarizirani.
Pri širenju elektromagnetskih valova (radiovalovi, mikrovalovi, svjetlost itd.) okomito na smjer širenja titraju električno i magnetsko polje
pa zato i oni mogu biti polarizirani.
Longitudinalni valovi ne mogu biti polarizirani.
Kakvi su valovi zvuka: transverzalni ili logintudidalni?
Zvuk se kroz plinove i tekućine širi kao longitudinalni val, a kroz čvrsta tijela može i kao transverzalni val.
Točan odgovor je: valovi zvuka u zraku ili vodi ne mogu biti polarizirani.
18. zadatak
Koja je od navedenih tvrdnja postulat specijalne teorije relativnosti?
- A. Brzina svjetlosti ista je u svim inercijskim referentnim sustavima.
- B. Vrijeme teče sporije u sustavu koji se giba.
- C. Količina gibanja ista je u svim inercijskim referentnim sustavima.
- D. Tijelo koje se giba izgleda kraće u smjeru gibanja.
Pomoć potražite na poveznici Osnovni postulati specijalne teorije relativnosti.
Odgovor je na poveznici Osnovni postulati specijalne teorije relativnosti.
19. zadatak
Koliku će duljinu štapa mjeriti mirni promatrač sa Zemlje ako se štap nalazi u letjelici koja se giba pored Zemlje brzinom \(0,8\,c\)? Vlastita duljina štapa iznosi \(10\,\textrm{cm}\). Štap je položen svojom duljinom u smjeru gibanja letjelice.
- A. \(0\,\textrm{cm}\)
- B. \(6\,\textrm{cm}\)
- C. \(10\,\textrm{cm}\)
- D. \(16,67\,\textrm{cm}\)
Duljinu štapa u sustavu u kojemu štap miruje označavamo s \(L_{0}\) i nazivamo vlastita duljina. Duljinu istoga štapa koju mjeri promatrač u odnosu na kojega se štap giba označavamo s \(L\). \[L=L_{0}\sqrt{1-v^{2}/c^{2}}\]
Promatrač u odnosu na kojega se štap giba izmjeri duljinu: \[ \begin{matrix} \begin{align*} &L_{0}=10\,\textrm{cm}\\ &v=0,8\,c\\ &L=L_{0}\sqrt{1-v^{2}/c^{2}}\\ &L=6\,\textrm{cm}\\ \end{align*} \end{matrix} \] Zadatak se mogao riješiti i bez računanja. Zbog kontrakcije duljine štap je kraći pa odgovori C i D otpadaju. Otpada i odgovor A jer bi se štap trebao gibati brzinom svjetlosti, a to nije moguće.
20. zadatak
Kako se može povećati maksimalna kinetička energija izbačenih elektrona pri fotoelektričnome efektu?
- A. smanjivanjem frekvencije upadnoga zračenja
- B. povećavanjem frekvencije upadnoga zračenja
- C. povećavanjem valne duljine upadnoga zračenja
- D. povećavanjem intenziteta upadnoga zračenja
Pomoć potražite na stranici Fotoelektrični efekt.
Energija fotona upadnog zračenja \(E_{f}\) pretvara se u rad potreban za izbacivanje elektrona iz metala \(W_{i}\) i u kinetičku energiju izbačenog elektrona \(E_{k}\): \[E_{f}=W_{i}+E_{k}\] Energija fotona jednaka je: \[E_{f}=h\,f\] pa je kinetička energija izbačenih elektrona: \[E_{k}=h\,f-W_{i}\] Iz posljednjeg izraza zaključujemo da je kinetička energija izbačenih elektrona proporcionalna frekvenciji upadnog zračenja.
21. zadatak
Čemu je jednak maseni broj atoma?
- A. broju neutrona u atomu
- B. broju protona u atomu
- C. broju nukleona u atomu
- D. broju elektrona u atomu
Jezgru atoma kemijskog elementa kojemu je simbol \(X\) zapisujemo kao \(_{\textrm{Z}}^{\textrm{A}}\textrm{X}\).
U jezgri atoma \(_{\textrm{Z}}^{\textrm{A}}\textrm{X}\) atomski (protonski) broj Z određuje broj protona, a maseni (nukleonski) broj A jednak je broju protona i neutrona u jezgri. Protone i neutrone nazivamo nukleoni.
22. zadatak
Koji zakon očuvanja ima za posljedicu Bernoullijevu jednadžbu?
- A. zakon očuvanja količine gibanja
- B. zakon očuvanja količine naboja
- C. zakon očuvanja energije
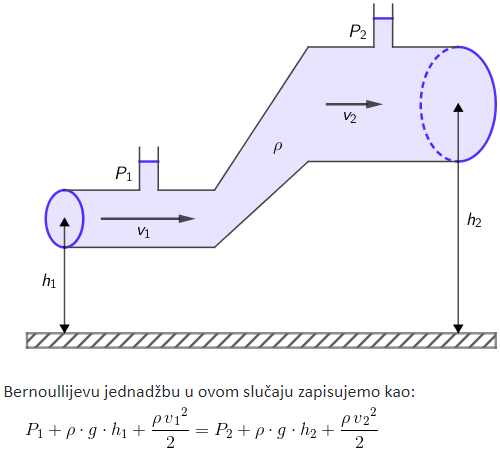
Bernoullijeva jednadžba posljedica je zakona očuvanja energije.
23. zadatak
Tijelo ovješeno na elastičnu oprugu titra periodom \(T\) na planetu P, a periodom \(T_{1}\) na planetu P1 .
Ubrzanje sile teže na planetu P veće je od ubrzanja sile teže na planetu P1 .
Kako se odnose periodi titranja?
- A. \(T_{1} > T\)
- B. \(T_{1} < T\)
- C. \(T_{1} = T\)
U knjižici formula za period titranja tijela na elastičnoj opruzi možete pronaći: \[T=2\pi\sqrt{\frac{m}{k}}\] Period titranja ovisi o masi tijela i konstanti elastičnosti opruge.
Period titranja tijela ovješenog na elastičnu oprugu ne ovisi o akceleraciji sile teže.
24. zadatak
Foton ultraljubičastoga zračenja ima energiju \(E_{1}\), a foton infracrvenoga zračenja ima energiju \(E_{2}\).
Koji od navedenih izraza vrijedi za njihove energije?
- A. \(E_{1} > E_{2}\)
- B. \(E_{1} < E_{2}\)
- C. \(E_{1} = E_{2}\)
Energija fotona elektromagnetskih valova može se prikazati kao: \[E=hf\] ili pomoću valne valne duljine: \[E=\frac{hc}{\lambda}\]
Iz izraza: \[E=hf\] zaključujemo kako je energija fotona proporcionalna frekvenciji elektromagnetskih valova. Frekvencija ultraljubičastog zračenja veća je od frekvencije infracrvenog zračenja.
25. zadatak
Graf prikazuje ovisnost položaja tijela o vremenu za tijelo koje se giba jednoliko po pravcu.
Koliko iznosi srednja brzina tijela tijekom gibanja?
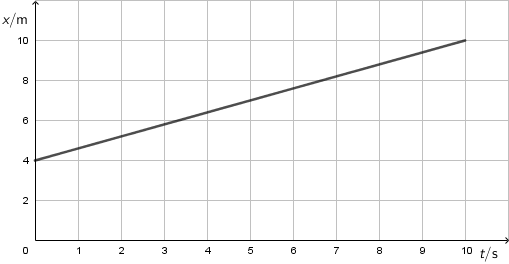
Odgovor:
Iz ovoga \(x\), \(t\) grafa iznos srednje brzine možemo odrediti kao: \[\overline{v}=\frac{\Delta x}{\Delta t}\]
Iznos srednje brzine jednak je: \[\overline{v}=\frac{\Delta x}{\Delta t}=\frac{x_{10}-x_{0}}{t_{10}-t_{0}}=\frac{10-4}{10-0}\] \[\overline{v}=0,6\,\textrm{m/s}\]
26. zadatak
Koliki tlak stvara čovjek mase \(76\,\textrm{kg}\) na površinu \(0,048\, \textrm{m}^2\)?
Rezultat zaokružite na dvije decimale.
Odgovor: kPa
Tlak je definiran kao sila koja djeluje na jediničnu površinu: \[P=\frac{F}{S}\]
Sila kojom čovjek djeluje na površinu \(S=0,048\,\textrm{m}^2\) jednaka je težini čovjeka \(F_{g}=m\,g\) pa je tlak jednak: \[P=\frac{F_{g}}{S}=\frac{m\,g}{S}=15,83\,\textrm{kPa}\]
27. zadatak
Voda mase \(m\) i temperature \(90\,^{0}\textrm{C}\) dodana je u posudu s vodom mase \(2\,m\) i temperature \(45\,^{0}\textrm{C}\).
Kolika će biti konačna temperatura vode nakon uspostavljanja termodinamičke ravnoteže?
Zagrijavanje okoline i posude je zanemarivo.
Odgovor: \(^0\textrm{C}\)
Toplina koju tijelo zagrijavanjem primi ili hlađenjem preda može se prikazati kao: \[Q=m\,c\,(t_{2}-t_{1})\] Početna temperatura je \(t_{1}\), a konačna \(t_{2}\). Toplina je pozitivna ako se tijelo zagrijava (prima toplinu), a negativna ako se hladi (predaje toplinu).
Uvedimo sljedeće oznake: \[ \begin{matrix} \begin{align*} &t_{1}\qquad(\textrm{temperatura}\;\textrm{toplije}\;\textrm{vode})\\ &t_{2}\qquad(\textrm{temperatura}\;\textrm{hladnije}\;\textrm{vode})\\ &t\qquad(\textrm{temperatura}\;\textrm{toplinske}\;\textrm{ravnoteže}) \end{align*} \end{matrix} \] Za temperaturu toplinske ravnoteže vrijedi: \[t_{1}>t>t_{2}\] Toplija voda predaje toplinu \(Q_{1}\): \[Q_{1}=mc\left ( t-t_{1} \right )\qquad(Q_{1} < 0)\] Hladnija voda prima toplinu \(Q_{2}\): \[Q_{2}=2mc\left (t_{2}-t \right )\qquad(Q_{2} > 0)\] Sustav je zatvoren pa je \(Q_{1}=Q_{2}\): \[mc\left ( t-t_{1} \right )=2mc\left (t_{2}-t \right )\] Iz ovoga izraza dobijemo temperaturu toplinske ravnoteže: \[t=\frac{t_{1}+2\,t_{2}}{3}=60\,^0\textrm{C}\]
28. zadatak
Magnetsko polje na udaljenosti \(5\,\textrm{cm}\) od ravnoga vodiča kojim teče struja iznosi \(10^{-4} \textrm{T}\).
Koliko iznosi struja koja teče kroz taj vodič?
Odgovor:
Magnetsko polje u točki koja se nalazi na udaljenosti \(r\) od dugog ravnog vodiča kojim prolazi struja \(I\) iznosi: \[B=\frac{\mu_{0}}{2\pi}\frac{I}{r}\]
Iz izraza za magnetsko polje: \[B=\frac{\mu_{0}}{2\pi}\frac{I}{r}\] za struju dobijemo: \[I=\frac{2\pi}{\mu_{0}}\,rB=25\,\textrm{A}\]
29. zadatak
Intenzitet zvuka iznosi \(10^3\,\textrm{W}/\textrm{m}^{2}\).
Koliko iznosi razina intenziteta toga zvuka ako je prag čujnosti \(10^{‒12}\,\textrm{W}/\textrm{m}^{2}\)?
Odgovor:
Razina intenziteta zvuka jednaka je: \[L=10\,\textrm{log}\frac{I}{I_{0}}\]
\begin{matrix} \begin{align*} &I=10^3\,\textrm{W}/\textrm{m}^{2}\\ &I_{0}=10^{‒12}\,\textrm{W}/\textrm{m}^{2}\\ &L=10\,\textrm{log}\frac{I}{I_{0}}\\ &L=150\,\textrm{dB} \end{align*} \end{matrix}
30. zadatak
U elektronskome se mikroskopu elektron giba brzinom \(10^{6}\,\textrm{m}/\textrm{s}\).
Kolika je valna duljina toga elektrona?
Odgovor: m
Pomoć potražite na poveznici De Broglieva valna duljina.
De Broglieva valna duljina jednaka je: \[\lambda =\frac{h}{mv }=7,28\cdot 10^{-10}\,\textrm{m}\]
31. zadatak
Tijelo A mase \(2\,\textrm{kg}\) i tijelo B mase \(3\,\textrm{kg}\) leže na horizontalnoj podlozi i međusobno se dodiruju kao što je prikazano na slici.
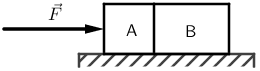
Na tijelo A djeluje horizontalna sila \(F=10\,\textrm{N}\).
Kolikom silom tijelo B djeluje na tijelo A?
Trenje je zanemarivo.
Odgovor:
Primjenom temeljnog zakona gibanja zaključujemo da će se oba tijela gibati akceleracijom kojoj je iznos: \[a=\frac{F}{m_{A}+m_{B}}\] Koje sile djeluju na tijelo A?
Iznos akceleracije kojom se gibaju oba tijela jednak je: \[a=\frac{F}{m_{A}+m_{B}}=2\,\textrm{m}/\textrm{s}^2\] Na tijelo A djeluje vanjska sila \(\vec{F}\) i tijelo B silom \(\vec{F}_\textrm{BA}\).
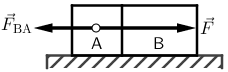
Sile \(\vec{F}\) i \(\vec{F}_\textrm{BA}\) imaju jednak smjer i suprotnu orijentaciju pa se iznos rezultantne sile na tijelo A dobije oduzimanjem iznosa manje sile od iznosa veće sile: \[F_\textrm{R}=F-F_\textrm{BA}\qquad(1)\] Ta sila ubrzava tijelo A akceleracijom \(2\,\textrm{m}/\textrm{s}^2\): \[F_\textrm{R}=m_\textrm{A}\cdot{a}= 4\,\textrm{N}\] Silu kojom tijelo B djeluje na tijelo A dobijemo iz izraza (1): \[F_\textrm{BA}=F-F_\textrm{R}=6\,\textrm{N}\]
32. zadatak
U Carnotovu kružnome procesu radno tijelo je hladnijemu spremniku temperature \(150\,^{0}\textrm{C}\) predalo
\(1,26\,\textrm{MJ}\) topline. Temperatura toplijega spremnika je \(300\,^{0}\textrm{C}\).
Koliki je rad u tome kružnom procesu obavilo radno tijelo?
Odgovor: kJ
Toplinski stroj koji od toplijeg spremnika temperature \(T_{1}\) prima toplinu \(Q_{1}\), a hladnijem spremniku temperature \(T_{2}\) predaje toplinu \(\left | Q_{2} \right |\), u jednom kružnom ciklusu obavi rad: \[W=Q_{1}-\left | Q_{2} \right |\]
Za Carnotov toplinski stroj vrijedi: \[\frac{Q_{1}}{\left | Q_{2} \right |}=\frac{T_{1}}{T_{2}}\] Iz ovoga izraza za toplinu koju stroj primi od toplijeg spremnika dobijemo: \[Q_{1}=\left | Q_{2} \right |\frac{T_{1}}{T_{2}}=1,707\cdot 10^{6}\,\textrm{J}\] Koristan rad stroja je: \[W=Q_{1}-\left | Q_{2} \right |=4,47\cdot 10^{5}\,\textrm{J}\]
33. zadatak
Na izvor napona \(150\,\textrm{V}\) priključen je kondenzator kapaciteta \(2\,\textrm{nF}\), a na izvor napona \(250\,\textrm{V}\)
kondenzator kapaciteta \(3\,\textrm{nF}\). Kondenzatori se odspoje i zatim međusobno spoje paralelno.
Koliki je zajednički napon na kondenzatorima nakon spajanja?
Odgovor:
Dok su spojeni na izvor napona kondenzatori se nabiju nabojima \(q_{1}=C_{1}\cdot U_{1}\) i \(q_{2}=C_{2}\cdot U_{2}\). Nakon što kondenzatore odspojimo s izvora napona i spojimo ih paralelno ukupni naboj ostaje očuvan: \[q=q_{1}+q_{2}\]
Ukupni kapacitet paralelno spojenih kondenzatora: \[C=C_{1}+C_{2}\] Ukupni naboj na kondenzatorima je: \[q=q_{1}+q_{2}\] Napon na svakom kondenzatoru je: \[U=\frac{q}{C}=\frac{q_{1}+q_{2}}{C_{1}+C_{2}}=210\,\textrm{V}\]
34. zadatak
Novčić promjera \(3\,\textrm{cm}\) postavljen je uspravno na udaljenosti \(24\,\textrm{cm}\) od konvergentne leće koja ima žarišnu daljinu
\(16\,\textrm{cm}\).
1. Na kojoj udaljenosti od leće nastaje slika novčića?
Odgovor:
2. Koliki je promjer nastale slike?
Odgovor:
Jednadžba leće povezuje udaljenost predmeta \(a\), udaljenost slike \(b\) i žarišnu udaljenost \(f\): \[\frac{1}{a}+\frac{1}{b}=\frac{1}{f}\]
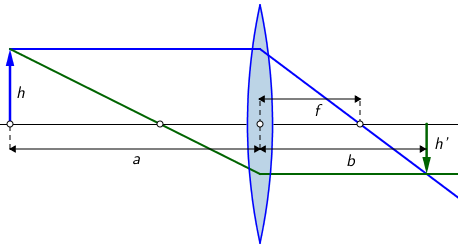
Linearno povećanje leće definiramo kao omjer visine slike i visine predmeta: \[m=\frac{h'}{h}\] Povećanje možemo izraziti i preko udaljenosti predmeta i slike od leće kao: \[m=-\frac{b}{a}\]
Pomoću jednadžbe leće možemo odrediti položaj slike: \[ \begin{matrix} \begin{align*} &\frac{1}{a}+\frac{1}{b}=\frac{1}{f}\\ &\frac{1}{b}=\frac{1}{f}-\frac{1}{a}\\ &b=48\,\textrm{cm} \end{align*} \end{matrix} \] Sada možemo odrediti i linearno povećanje leće: \[m=-\frac{b}{a}=-2\] Visinu slike odredimo pomoću linearnog povećanja: \[h'=m\cdot h=-6\,\textrm{cm}\] Predznak minus je zbog toga što je slika obrnuta u odnosu na predmet.
35. zadatak
Graf prikazuje ovisnost broja neraspadnutih čestica \(N\) nekoga radioaktivnog elementa o vremenu \(t\).
Kolika je aktivnost uzorka toga elementa u kojemu se nalazi 2016 čestica?
Rezultat zapišite pomoću znanstvenog zapisa s tri decimalna mjesta.
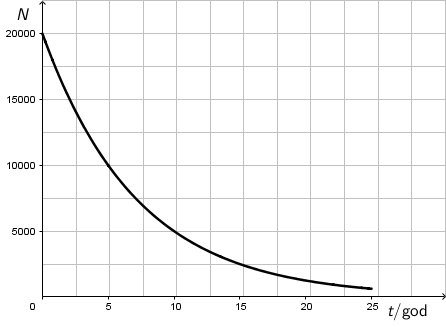
Odgovor:
Ako neki radioaktivni uzorak u početnom trenutku sadrži \(N_{0}\) jezgri, tijekom vremena taj će se broj smanjivati. Nakon vremena \(T\), kojega nazivamo vrijeme poluraspada, preostat će \(N_{0}/2\) jezgri, nakon još jednog vremena poluraspada preostat će ih \(N_{0}/4\) itd. Broj neraspadnutih jezgri \(N\) smanjuje se eksponencijalno tijekom vremena \(t\): \[N=N_{0}e^{-\lambda t}\] Konstanta radioaktivnog raspada \(\lambda\) može se prikazati pomoću vremena poluraspada: \[\lambda=\frac{\textrm{ln}\,2}{T}\] Aktivnost radioaktivnog uzorka jednaka je: \[A=\lambda N\]
Iz grafa odredimo vrijeme poluraspada: \(T=5\,\textrm{god}\). Aktivnost uzorka jednaka je: \[ \begin{matrix} \begin{align*} &A=\lambda N\\ &\lambda=\frac{\textrm{ln}\,2}{T}\\ &A=\frac{\textrm{ln}\,2}{T}N\\ &A=8,862\cdot 10^{-6}\,\textrm{Bq} \end{align*} \end{matrix} \]