Probni ispit za maturu 2022. godine
1. zadatak
Na slici je prikazan graf ovisnosti brzine o vremenu za tri tijela A, B i C.
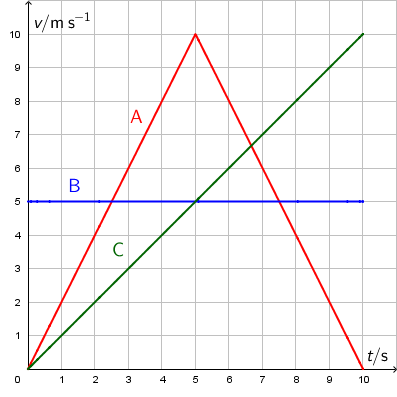
Kako se odnose putovi \(s_{\small{\textrm{A}}}\), \(s_{\small{\textrm{B}}}\) i \(s_{\small{\textrm{C}}}\) koje su tijela prešla za 10 sekundi?
- A. \(s_{\small{\textrm{A}}} > s_{\small{\textrm{B}}} > s_{\small{\textrm{C}}}\)
- B. \(s_{\small{\textrm{A}}} > s_{\small{\textrm{B}}} = s_{\small{\textrm{C}}}\)
- C. \(s_{\small{\textrm{A}}} = s_{\small{\textrm{B}}} > s_{\small{\textrm{C}}}\)
- D. \(s_{\small{\textrm{A}}} = s_{\small{\textrm{B}}} = s_{\small{\textrm{C}}}\)
Iz \(v,t\) grafa put određujemo kao površinu ispod grafa.
Odredimo putove tako da izračunamo površinu ispod grafa A, B i C.
Graf A \[s_{\small{\textrm{A}}}=\frac{10\,\cdot 10}{2}=50\,\textrm{m}\]
Graf B \[s_{\small{\textrm{B}}}=5\cdot 10=50\,\textrm{m}\]
Graf C \[s_{\small{\textrm{C}}}=\frac{10\,\cdot 10}{2}=50\,\textrm{m}\]
Sva tri puta su jednaka.
2. zadatak
Na tijelo mase \(m\) uvijek duž istoga pravca djeluje ukupna promjenjiva sila čiji se iznos smanjuje u vremenu, no nikad ne postane nula.
Kako se zbog toga giba tijelo?
- A. Prvo se giba ubrzano, zatim jednoliko, a zatim usporeno.
- B. Prvo se giba ubrzano, a zatim usporeno.
- C. Prvo se giba ubrzano, a zatim jednoliko.
- D. Cijelo se vrijeme giba ubrzano.
- Ako je ukupna sila koja djeluje na tijelo jednaka nuli, akceleraija tijela je \(a=0\) i gibanje je jednoliko.
- Ako je ukupna sila koja djeluje na tijelo konstantna, akceleraija tijela je \(a=\textrm{konst.}\) i gibanje je jednoliko ubrzano.
- Ako je ukupna sila koja djeluje na tijelo promjenjiva, akceleraija tijela također je promjenjiva i gibanje je ubrzano, ali s akceleracijom koja se mijenja.
Graf prikazuje silu koja djeluje na tijelo i koja se tijekom vremena smanjuje, no nikada ne postane jednaka nuli.
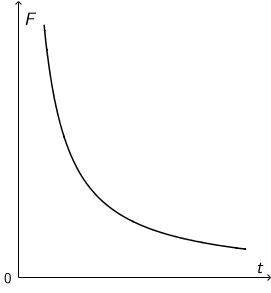
Akceleracija tijela tijekom vremena se smanjuje, ali nikada ne postane jednaka nuli. To znači da se prirast brzine tijekom vremena smanjuje, ali brzina tijela se stalno povećava.
Primjer
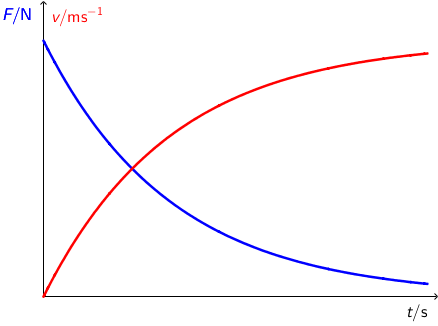
Na slici plavom bojom označen je graf sile koja se tijekom vremena smanjuje, ali nikada ne postane jednaka nuli.
Masa tijela je \(1\,\textrm{kg}\).
Crvenom je bojom označen graf brzine. Iz grafa vidimo da se tijelo cijelo vrijeme giba ubrzano.
3. zadatak
Tijelo se giba jednoliko po kružnici stalnoga polumjera centripetalnom akceleracijom \(a_{\textrm{cp}}\).
Koliki je iznos centripetalne akceleracije toga tijela ako mu se kutna brzina poveća 3 puta, a polumjer kruženja ostane isti?
- A. \(\Large{\frac{a_{\textrm{cp}}}{9}}\)\(\\\)
- B. \(\Large{\frac{a_{\textrm{cp}}}{3}}\)
- C. \(3\,a_{\textrm{cp}}\)
- D. \(9\,a_{\textrm{cp}}\)
Tijelo se giba jednoliko po kružnici polumjera \(r\). U početnom trenutku nalazi se u položaju A, a nakon vremena \(\Delta t\) nađe se u položaju B.
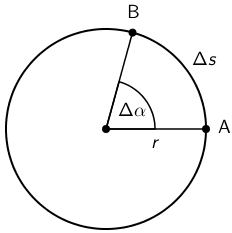
Obodna brzina
Za vrijeme \(\Delta t\) tijelo opiše kružni luk \(\overset{\huge\frown}{\rm{AB}}\) duljine \(\Delta s\). Obodnu brzinu definiramo kao:
\[v=\frac{\Delta s}{\Delta t}\]
Nakon što tijelo obiđe jedan puni krug duljina kružnog luka jednaka je opsegu kružnice \(\Delta s=2\,r\,\pi\), a interval vremena \(\Delta t\) jednak je
ophodnom vremenu \(\Delta t=T\). Obodna brzina jednaka je:
\[v=\frac{2\,r\,\pi}{T}\qquad(1)\]
Kutna brzina
Za vrijeme \(\Delta t\) polumjer kružnice opiše kut \(\Delta \alpha\). Kutnu brzinu definiramo kao:
\[\omega=\frac{\Delta \alpha}{\Delta t}\]
Nakon što tijelo obiđe jedan puni krug, polumjer kružnice opiše puni kut \(\Delta \alpha=2\,\pi\,\textrm{rad}\). Kutna brzina jednaka je:
\[\omega=\frac{2\,\pi}{T}\qquad(2)\]
Usporedbom izraza (1) i (2) dobivamo izraz koji povezuje obodnu i kutnu brzinu:
\[v=\omega\,r\]
4. zadatak
Satelit Starlink giba se na stalnoj visini iznad površine Zemlje nekom brzinom. Masa satelita iznosi 250 kg.
Koliki bi bio iznos brzine kojom bi se gibao po jednakoj putanji kada bi mu masa iznosila 500 kg?
- A. Brzina satelita u drugome bi slučaju trebala biti dva puta manja nego u prvome slučaju.
- B. Brzina satelita u drugome bi slučaju trebala biti jednaka kao i u prvome slučaju.
- C. Brzina satelita u drugome bi slučaju trebala biti dva puta veća nego u prvome slučaju.
- D. Brzina satelita u drugome bi slučaju trebala biti četiri puta veća nego u prvome slučaju.
Koja sila ima ulogu centripetalne sile?
Brzina kojom se satelit giba oko Zemlje ne ovisi o njegovoj masi pa se zbog toga njegova brzina neće promijeniti.
5. zadatak
Dva čavla od istoga metala, od kojih je jedan dvostruko duži od drugoga na temperaturi \(10\,^{\circ}\textrm{C}\), leže jedan pored drugoga. Kada se
temperatura okoline u kojoj se nalaze čavli poveća na \(40\,^{\circ}\textrm{C}\), čavli se produlje.
Koja je od navedenih tvrdnja o produljenjima čavala točna?
- A. Kraći se čavao više produlji od dužega.
- B. Oba se čavla jednako produlje.
- C. Duži se čavao dvostruko više produlji od kraćega.
- D. Duži se čavao više od dvostruko produlji od kraćega čavla.
- \(\ell_{0}\) - duljina čavla pri početnoj temperaturi \(t_{0}\)
- \(\ell\) - duljina čavla pri konačnoj temperaturi \(t\)
- \(\Delta t=t-t_{0}\) - promjena temperature
Dulji će se čavao dva puta više produljiti od kraćeg čavla.
6. zadatak
Pri kojemu se od navedenih tlakova realni plin ponaša najsličnije idealnomu plinu?
- A. pri 1 bar
- B. pri 1 kbar
- C. pri 1 Mbar
- D. pri 1 Gbar
Svojstva plina pri visokim tlakovima razlikuju se od svojstava idealnog plina. Jednadžbu stanja idealnog plina \[p\,V=N\,k\,T\] možemo, pod određenim uvjetima, primijeniti i na realne plinove. To je moguće ako tlak nije prevelik i ako je temperatura plina puno veća od temperature pri kojoj plin prelazi u tekuće stanje.
Jednadžba stanja idealnog plina može se primijeniti pri niskom tlaku.
7. zadatak
Latentna toplina isparavanja vode iznosi 2,26 MJ/kg. Specifični toplinski kapaciteti vode, pare i leda iznose redom
4200 J/kgK, 2100 J/kgK i 2100 J/kgK.
Latentna toplina taljenja leda iznosi 330 kJ/kg.
Što će preostati kada se jednomu kilogramu vodene pare temperature \(100\,^{\circ}\textrm{C}\) oduzme 2 MJ topline?
- A. samo vodena para
- B. smjesa vodene pare i vode
- C. samo voda
- D. smjesa vode i leda
Toplina zagrijavanja
\[Q=m\,c\,\Delta t\]
\(m\)-masa tijela
\(c\)-specifični toplinski kapacitet tijela
Toplina potrebna da se jednom kilogramu neke tvari temperatura povisi za jedan stupanj.
\(\Delta t\)-porast temperature tijela
Toplina isparavanja
\[Q_{\textrm{i}}=r\,m\]
\(m\)-masa tijela
\(r\) - specifična toplina isparavanja ili latentna toplina isparavanja
Toplina potrebna da jedan kilogram tvari u tekućem agregatnom stanju potpuno ispari.
Jedinica za \(r\): \(\textrm{J}/\textrm{kg}\)
Toplina taljenja
\[Q_{\textrm{t}}=\lambda\,m\]
\(m\)-masa tijela
\(\lambda\) - specifična toplina taljenja
Toplina potrebna da se jedan kilogram tvari u čvrstom agregatnom stanju potpuno rastali.
Jedinica za \(\lambda\): \(\textrm{J}/\textrm{kg}\)
Kada bismo jednom kilogramu vodene pare pri \(100\,^{\circ}\textrm{C}\) oduzeli 2,26 MJ topline, sva bi se para kondenzirala u vodu temperature \(100\,^{\circ}\textrm{C}\). Ako oduzmemo 2 MJ topline, kondenzirat će se: \[m=\frac{Q}{r}=\frac{2}{2,26}=0,88\,\textrm{kg}\] pare u vodu.
Prema tome, preostaje 0,88 kg vode i 0,12 kg pare.
8. zadatak
Toplinski stroj obavi 1 kJ rada za svakih 4 kJ uložene energije.
Koja od navedenih tvrdnja vrijedi za ovaj toplinski stroj?
- A. Korisnost stroja veća je od 100 %.
- B. Korisnost stroja manja je od 100 %.
- C. Stroj radi bez spremnika niže temperature.
- D. Stroj radi bez spremnika više temperature.
Korisnost toplinskog stroja \(\eta\) \[\eta=\frac{W}{Q_{1}}\]
- W - korisni rad kojega obavi stroj
- \(Q_{1}\) - toplina koju stroj prima od toplijeg spremnika (uložena energija)
\[\eta=\frac{W}{Q_{1}}=\frac{1}{4}=0,25\] \[\eta=25\,\%\]
Napomena
Zadatak se može riješiti bez računanja.
Svaki toplinski stroj mora imati dva spremnika, a korisnost toplinskog stroja manja je od \(100\%.\)
9. zadatak
Dva naboja \(q_{1}=+q\) i \(q_{2}=-2\,q\) učvršćena su u praznome prostoru.
Koliki je iznos ukupnoga električnog polja \(E\) u točki koja se nalazi na polovištu njihove spojnice?
- A. \(E=E_{1}-E_{2}\)
- B. \(E=E_{2}-E_{1}\)
- C. \(E=E_{1}+E_{2}\)
- D. \(E=0\)
Rezultantno električno polje dva naboja \(q_{1}\) i \(q_{2}\) određujemo vektorskim zbrajanjem polja ta dva naboja.
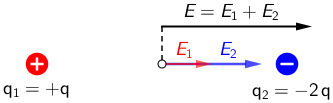
Električno polje točkastog naboja \[E=k\,\frac{q}{r^{2}}\] Oba polja imaju jednak smjer i orijentaciju. Iznos rezultantnog polja na polovištu spojnice naboja određujemo zbrajanjem iznosa oba polja.
10. zadatak
Pločasti kondenzator spojen je na bateriju napona \(U\).
Kolika je razlika potencijala među pločama kondenzatora ako se u njega umetne dielektrik bez odvajanja od izvora napona?
- A. \(0\)
- B. \(U/2\)
- C. \(U\)
- D. \(2\,U\)
Mijenja li se napon između ploča kondenzatora ako između ploča umetnemo dielektrik?
Umetanjem dielektrika mijenjaju se kapacitet i naboj na pločama. Napon između ploča jednak je naponu baterije na koju je spojen.
11. zadatak
Na istome rasvjetnom tijelu žarulja snage 100 W zamijenjena je žaruljom snage 25 W.
Dok je na rasvjetnome tijelu bila žarulja snage 100 W, njom je prolazila struja iznosa 1 A.
Koliki je otpor žarulje snage 25 W?
- A. \(100\,\Omega\)
- B. \(200\,\Omega\)
- C. \(300\,\Omega\)
- D. \(400\,\Omega\)
Snaga žarulje kroz koju prolazi struja \(I\):
\[P=U\,I\]
gdje je \(U\) napon na krajevima žarulje.
Prema potrebi možemo koristiti i Ohmov zakon:
\[U=I\,R\]
gdje je \(R\) otpor žarulje.
Kroz žarulju snage \(P_{1}=100\,\textrm{W}\) prolazi struja 1 A. Napon na krajevima te žarulje je: \[U=\frac{P_{1}}{I}=100\,\textrm{V}\] Ako žarulju snage 100 W zamjenimo žaruljom snage 25 W, napon na njezinim krajevima ostaje isti: \[P_{2}=U\,I_{2} = \frac{U^{2}}{R}\] \[R=\frac{U^{2}}{P_{2}}=\frac{100^{2}}{25}=400\,\Omega\]
12. zadatak
Štapičasti magnet slobodno pada kroz metalni prsten.
Koja je od navedenih tvrdnja istinita u trenutku ulaska magneta kroz prsten kao što je prikazano na slici?
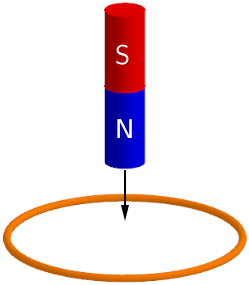
- A. Smjer inducirane struje u prstenu poklapa se sa smjerom gibanja kazaljke na satu.
- B. Smjer inducirane struje u prstenu obrnut je od smjera gibanja kazaljke na satu.
- C. Smjer inducirane struje u prstenu upravo se mijenja.
- D. U prstenu nema inducirane struje.
Lenzovo pravilo
Prema Faradayovom zakonu inducirani elektromotorni napon u vodiču koji se nalazi u promjenjivom magnetskom polju jednak je:
\[U_{\textrm{i}}=-\frac{\Delta \phi}{\Delta t}\]
Predznak minus je zbog Lenzovog pravila: Inducirani elektromotorni napon u vodiču uzrokuje induciranu struju koja stvara magnetski tok koji je
suprotan promjeni magnetskog toka koji je uzrok indukcije.
Pokrenite video.
Gibanje magneta na ulazu u metalni obruč inducira struju koja stvara magnetsko polje suprotnog smjera od magnetskog polja štapičastog magneta. Struja ima smjer koji je suprotan smjeru gibanja kazaljke sata. Pri izlasku iz obruča inducirana struja ima suprotan smjer.
Okrenimo magnet tako da u obruč ulazi najprije južni pol magneta. Pokrenite video.
Gibanje magneta na ulazu u metalni obruč inducira struju koja stvara magnetsko polje suprotnog smjera od magnetskog polja štapičastog magneta. Struja ima smjer koji je je jednak smjeru gibanja kazaljke sata. Pri izlasku iz obruča inducirana struja ima suprotan smjer.
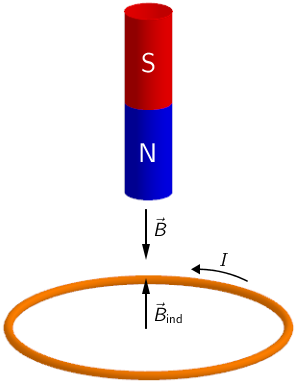
Inducirano magnetsko polje na osnovu Lenzovog pravila mora imati suprotan smjer od magnetskog polja štapičastog magneta.
Obruč obuhvatimo desnom rukom tako da palac pokazuje smjer induciranog magnetskog polja. Savijeni prsti pokazuju smjer inducirane struje.
Na slici vidimo da je taj smjer suprotan smjeru gibanja kazaljke sata.
13. zadatak
Koja od navedenih jednadžbi opisuje iznos sile \(F\) na tijelo tijekom harmonijskoga titranja?
- A. \(F=0,5\,\sqrt{x}\)
- B. \(F=2,4\,x\)
- C. \(F=8\,x^{2}\)
- D. \(F=\large{\frac{1,2}{x}}\)
Tijelo će harmonijski titrati ako na njega djeluje harmonijska sila. Harmonijska sila proporcionalna je elongaciji, a smjer joj je suprotan smjeru elongacije. \[\vec{F}=-k\,\vec{x}\]
Iznos harmonijske sile proporcionalan je iznosu elongacije: \[F=k\,x\] Točan odgovor je B.
14. zadatak
Potresni val na površini Zemlje proizvede vodeni val koji možemo smatrati sinusoidalnim transverzalnim valom. Brzina takvoga vala iznosi
2,5 m/s, a frekvencija 0,5 Hz.
Kako glasi jednadžba toga vala?
- A. \(y=A\,\textrm{sin}\,2\,\pi\large{\left(\frac{t}{2\,\textrm{s}}-\frac{x}{1,25\,\textrm{m}}\right)}\)
- B. \(y=A\,\textrm{sin}\,2\,\pi\large{\left(\frac{0,5\,t}{1\,\textrm{s}}-\frac{x}{2,5\,\textrm{m}}\right)}\)
- C. \(y=A\,\textrm{sin}\,2\,\pi\large{\left(\frac{t}{0,5\,\textrm{s}}-\frac{x}{5\,\textrm{m}}\right)}\)
- D. \(y=A\,\textrm{sin}\,2\,\pi\large{\left(\frac{0,5\,t}{1\,\textrm{s}}-\frac{x}{5\,\textrm{m}}\right)}\)
Jednadžba transverzalnog vala: \[y=A\,\textrm{sin}\left (\omega \,t - k\,x\right)\]
- \(A\) - amplituda vala
- \(\omega=\large{\frac{2\,\pi}{T}}\) - kružna ili kutna frekvencija
- \(k=\large{\frac{2\,\pi}{\lambda}}\) - valni broj
Valnu jednadžbu moguće je zapisati i u obliku: \[y=A\,\textrm{sin}\left(\frac{2\,\pi}{T}\,t-\frac{2\,\pi}{\lambda}\,x\right)\]
- \(T\) - period titranja izvora vala
- \(\lambda\) - valna duljina
Period titranja odredimo pomoću frekvencije: \[T=\frac{1}{f}=2\,\textrm{s}\] Valnu duljinu odredimo pomoću brzine širenja vala i perioda: \[\lambda=v\,T=5\,\textrm{m}\] \[y=A\,\textrm{sin}\left(\frac{\pi}{1\,\textrm{s}}\,t-\frac{2\,\pi}{5\,\textrm{m}}\,x\right)\]
15. zadatak
Deset jednakih električnih sirena proizvodi zvuk razine intenziteta 50 dB.
Koliko bi takvih sirena proizvelo zvuk razine intenziteta 60 dB?
- A. 20
- B. 60
- C. 100
- D. 200
Razina intenziteta zvuka jednaka je: \[L=10\,\textrm{log}\frac{I}{I_{0}}\] Pragu čujnosti \[I_{0}=10^{-12}\,\textrm{W}/\textrm{m}^{2}\] odgovara razina intenziteta od 0 dB
Razina intenziteta zvuka jedne sirene je:
\[L_{1}=10\,\textrm{log}\frac{I_{1}}{I_{0}}\]
Razina intenziteta zvuka deset jednakih sirene je:
\[L_{10}=10\,\textrm{log}\frac{I_{10}}{I_{0}}\]
Intenzitet zvuka deset jednakih sirena deset je puta veći od intenziteta jedne sirene
\[I_{10}=10\,I_{1}\]
\[L_{10}=10\,\textrm{log}\frac{10\,I_{1}}{I_{0}}\]
\[L_{10}=10\,\textrm{log}\,10+10\,\textrm{log}\,\frac{I_{1}}{I_{0}}\]
\[L_{10}=10+L_{1}\]
\[10+L_{1}=50\,\textrm{dB}\]
\[L_{1}=40\,\textrm{dB}\]
Dobili smo razinu intenziteta zvuka jedne sirene.
Razina intenziteta \(n\) jednakih sirena bit će:
\[L_{\textrm{n}}=10\,\textrm{log}\frac{I_{\textrm{n}}}{I_{0}}\]
\[I_{\textrm{n}}=n\,I_{1}\]
\[L_{\textrm{n}}=10\,\textrm{log}\frac{n\,I_{1}}{I_{0}}\]
\[L_{\textrm{n}}=10\,\textrm{log}\,n+10\,\textrm{log}\,\frac{I_{1}}{I_{0}}\]
\[L_{\textrm{n}}=10\,\textrm{log}\,n+L_{1}\]
\[10\,\textrm{log}\,n+40\,\textrm{dB}=60\,\textrm{dB}\]
\[10\,\textrm{log}\,n=20\,\textrm{dB}\]
\[\textrm{log}\,n=2\,\textrm{dB}\]
\[n=100\]
16. zadatak
Jakost leća naočala iznosi +2,5 dioptrija.
Koja od navedenih tvrdnja vrijedi za ove naočale?
- A. Leće naočala su divergentne, a koriste se za ispravljanje kratkovidnosti.
- B. Leće naočala su konvergentne, a koriste se za ispravljanje kratkovidnosti.
- C. Leće naočala su konvergentne, a koriste se za ispravljanje dalekovidnosti.
- D. Leće naočala su divergentne, a koriste se za ispravljanje dalekovidnosti.
Dalekovidno oko
Kada čovjek s dalekovidnim okom promatra neki predmet, svjetlosni snop koji dolazi od tog predmeta fokusira se na neko mjesto koje je iza mrežnice oka.
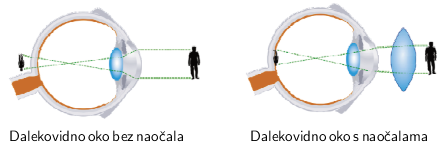
To se korigira pomoću naočala s konvergentnim lećama, koje se stavljaju ispred oka. (Žarišna daljina kombinacije dviju leća, leće naočala i očne leće, manja je od žarišne daljine same očne leće.) Na taj se način smanjuje žarišna daljina pa slika predmeta pada na mrežnicu. Starenjem se sposobnost akomodacije oka smanjuje jer leća gubi elastičnost, pa se najmanja daljina jasnog vida postupno povećava. Oko postaje sve dalekovidnije. U dobi od 10 godina najmanja je udaljenost jasnog vida oko 7 cm, a starenjem se postupno povećava i u dobi od 60 godina iznosi oko 2 m ili više.
Kratkovidno oko
Kratkovidno oko od upadnoga svjetlosnog snopa stvara sliku ispred očne mrežnice. To se korigira pomoću naočala s divergentnom lećom.
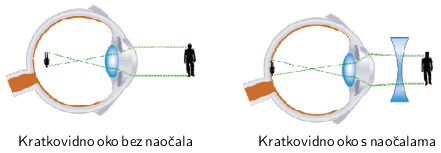
Konvergentne leće korigiraju dalekovidnost. Konvergentne leće imaju pozitivnu žarišnu daljinu, odnosno pozitivnu jakost (+2,5 dioptrija u zadatku).
17. zadatak
Prolaskom monokromatske svjetlosti kroz optičku rešetku određene konstante na zastoru nastaje ogibna slika.
Koji je od prikazanih uzoraka nastao upotrebom optičke rešetke najveće konstante?

- A. uzorak A
- B. uzorak B
- C. uzorak C
- D. uzorak D
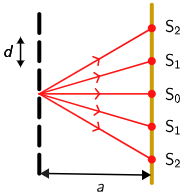
Iz jednadžbe za optičku rešetku \[d\,\textrm{sin}\,\alpha_{\textrm{k}}=k\,\lambda\] moguće je odrediti kutove pod kojima se vide ogibni maksimumi: \[\textrm{sin}\,\alpha_{\textrm{k}}=\frac{k\,\lambda}{d}\]
Kutovi pod kojima vidimo ogibne maksimume obrnuto su proporcionalni konstanti optičke rešetke. \[\textrm{sin}\,\alpha_{\textrm{k}}=\frac{k\,\lambda}{d}\] Ti su kutovi najmanji ako je konstanta optičke rešetke najveća.
18. zadatak
Elektromagnetski val širi se vakuumom.
Koja je od navedenih tvrdnja ispravna za brzinu toga elektromagnetskog vala?
- A. Povećanjem njegove frekvencije povećat će mu se brzina.
- B. Povećanjem njegove energije povećat će mu se brzina.
- C. Povećanjem njegove valne duljine povećat će mu se brzina.
- D. Nemoguće je povećati brzinu toga vala.
Elektromagnetski valovi u vakuumu šire se brzinom svjetlosti: \[c\approx 3\cdot 10^{8}\,\textrm{m/s}\]
Brzina svjetlosti u vakuumu je konstantna pa je točan odgovor D.
19. zadatak
Elektron i proton imaju istu de Broglievu valnu duljinu.
Koja je od navedenih tvrdnja za brzinu gibanja čestica i njihovu kinetičku energiju točna?
- A. Elektron ima veću brzinu i kinetičku energiju od protona.
- B. Proton ima veću brzinu i kinetičku energiju od elektrona.
- C. Elektron ima veću brzinu od protona, a proton veću kinetičku energiju od elektrona.
- D. Proton ima veću brzinu od elektrona, a elektron veću kinetičku energiju od protona.
De Broglieva valna duljina čestice mase \(m\) koja se giba brzinom \(v\): \[\lambda=\frac{h}{m\,v}\] Kinetička energija čestice: \[E_{\textrm{k}}=\frac{1}{2}\,m\,v^{2}\]
Izjednačimo de Broglievu valnu duljinu elektrona
\[\lambda_{\textrm{e}}=\frac{h}{m_{\textrm{e}}\,v_{\textrm{e}}}\]
s de Broglievom valnom duljinom protona
\[\lambda_{\textrm{p}}=\frac{h}{m_{\textrm{p}}\,v_{\textrm{p}}}\]
\[\frac{h}{m_{\textrm{e}}\,v_{\textrm{e}}}=\frac{h}{m_{\textrm{p}}\,v_{\textrm{p}}}\]
\[\frac{m_{\textrm{e}}\,v_{\textrm{e}}}{m_{\textrm{p}}\,v_{\textrm{p}}}=1\]
\[\frac{v_{\textrm{e}}}{v_{\textrm{p}}}=\frac{m_{\textrm{p}}}{m_{\textrm{e}}}\qquad(1)\]
\[m_{\textrm{p}} > m_{\textrm{e}}\Rightarrow v_{\textrm{e}} > v_{\textrm{p}}\]
Brzina elektrona veća je od brzine protona.
Odredimo omjer kinetičkih energija elektrona i protona:
\[\frac{E_{\textrm{ke}}}{E_{\textrm{kp}}}=\frac{1}{2}\,m_{\textrm{e}}\,v_{\textrm{e}}^{2}\cdot \frac{2}{m_{\textrm{p}}\,v_{\textrm{p}}^{2}}\]
\[\frac{E_{\textrm{ke}}}{E_{\textrm{kp}}}=\frac{m_{\textrm{e}}}{m_{\textrm{p}}}\cdot \left(\frac{v_{\textrm{e}}}{v_{\textrm{p}}}\right)^{2}\]
Uzmimo u obzir izraz (1):
\[\frac{E_{\textrm{ke}}}{E_{\textrm{kp}}}=\frac{m_{\textrm{e}}}{m_{\textrm{p}}}\cdot \left(\frac{m_{\textrm{p}}}{m_{\textrm{e}}}\right)^{2}\]
\[\frac{E_{\textrm{ke}}}{E_{\textrm{kp}}}=\frac{m_{\textrm{p}}}{m_{\textrm{e}}}\]
\[m_{\textrm{p}} > m_{\textrm{e}}\Rightarrow E_{\textrm{ke}} > E_{\textrm{kp}}\]
Kinetička energija elektrona veća je od kinetičke energije protona.
Točan odgovor je A.
20. zadatak
U jednome slučaju elektron u vodikovu atomu prelazi direktno iz stanja n = 5 u stanje m = 1,
a u drugome iz stanja n = 5 prvo prelazi u neko stanje k, a zatim u stanje m = 1.
U kojoj se od navedenih situacija ispusti foton najniže moguće energije?
- A. kada prelazi direktno u stanje m = 1
- B. kada prvo prelazi u stanje k = 2
- C. kada prvo prelazi u k = 3
- D. kada prvo prelazi u stanje k = 4
Prvih pet stacionarnih stanja shematski je prikazano na slici.
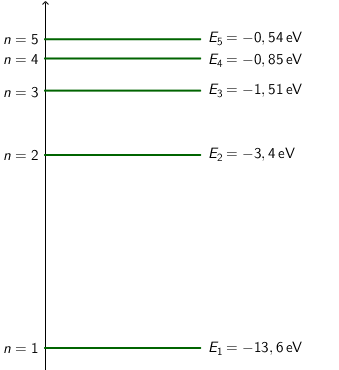
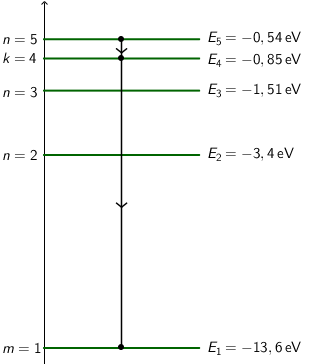
Prijelazom atoma iz stacionarnog stanja \(n=5\) u stacionarno stanje \(m=1\) dolazi do emisije fotona najveće energije (za stacionarna stanja prikazana na slici): \[E_{\textrm{f}}=E_{5}-E_{1}=13,06\,\textrm{eV}\] Prijelazom atoma iz stacionarnog stanja \(n=5\) u stacionarno stanje \(k=4\) dolazi do emisije fotona najniže energije (za stacionarna stanja prikazana na slici): \[E_{\textrm{f}}=E_{5}-E_{4}=0,31\,\textrm{eV}\] Točan odgovor je D (prijelaz atoma iz stacionarnog stanja \(n=5\) u stacionarno stanje \(k=4.\))
21. zadatak
Koji od navedenih izraza ne predstavlja moguću nuklearnu reakciju?
- A. \(^{10}\textrm{B}+^{4}\textrm{He}\rightarrow ^{13}\textrm{C}+^{1}\textrm{H}\)
- B. \(^{10}\textrm{B}+^{1}\textrm{n}\rightarrow ^{11}\textrm{B}+\gamma\)
- C. \(^{23}\textrm{Na}+^{1}\textrm{H}\rightarrow ^{20}\textrm{Ne}+^{4}\textrm{He}\)
- D. \(^{14}\textrm{N}+^{1}\textrm{H}\rightarrow ^{13}\textrm{C}+\beta^{+}\)
U nuklearnim reakcijama vrijede sljedeći zakoni očuvanja:
-
Očuvanje električnog naboja: \(Z_{1}+Z_{2}=Z_{3}+Z_{4}\).
Broj protona prije reakcije \(Z_{1}+Z_{2}\), jednak je broju protona nakon reakcije \(Z_{3}+Z_{4}\). Umjesto protona mogu biti i čestice naboja +e, -e, 0. Bitno je da ukupni naboj prije reakcije bude jednak ukupnom naboju nakon reakcije. -
Očuvanje broja nukleona: \(A_{1}+A_{2}=A_{3}+A_{4}\).
Broj nukleona prije reakcije \(A_{1}+A_{2}\), jednak je broju nukleona nakon reakcije \(A_{3}+A_{4}\). -
Očuvanje ukupne relativističke energije: \(E_{1}+E_{2}=E_{3}+E_{4}\).
Ukupna energija prije reakcije \(E_{1}+E_{2}\), jednaka je ukupnoj energiji nakon reakcije \(E_{3}+E_{4}\). -
Očuvanje količine gibanja: \(p_{1}+p_{2}=p_{3}+p_{4}\).
Ukupna količina gibanja prije reakcije \(p_{1}+p_{2}\), jednaka je ukupnoj količini gibanja nakon reakcije \(p_{3}+p_{4}\).
Prve tri jednadžbe zadovoljavaju očuvanje električnog naboja i očuvanje broja nukleona.
Četvrta jednadžba ne zadovoljava navedene zakone očuvanja.
\(\beta^{+}\) čestica je pozitron \({_{+1}^{\;\;0}}\textrm{e}\) (antičestica elektrona).
22. zadatak
Koji je od navedenih procesa glavni izvor energije u unutrašnjosti Sunca?
- A. nuklearna fuzija
- B. nuklearna fisija
- C. alfa-raspad
- D. beta-raspad
Nuklearna fuzija
Masa bilo koje stabilne jezgre manja je od ukupne mase slobodnih nukleona koji čine tu jezgru. Zato se izgradnjom takvih jezgara oslobađa energija. Fuzija je nuklearna reakcija u kojoj od slobodnih nukleona nastaje jezgra ili proces u kojemu se lake jezgre spajaju u teže jezgre uz oslobađanje energije.
Energija koja se stvara u Suncu jest energija oslobođena u procesima fuzije.
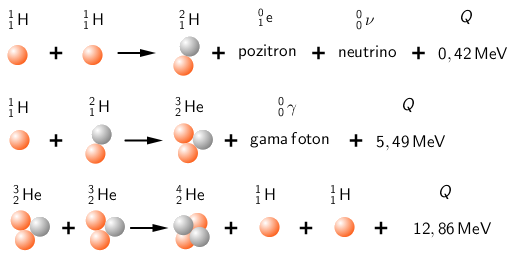
Reakcije prikazane na slici odvijaju se u uvjetima visokih temperatura na Suncu. Postizanje tako visokih temperatura na Zemlji glavnni je problem za korištenje energije fuzije na Zemlji.
Za nuklearnu fuziju najvažnije su reakcije između jezgara najlakših atoma \(_{1}^{2}\textrm{H}\) (deuterij), \(_{1}^{3}\textrm{H}\) (tricij) i \(_{2}^{3}\textrm{He}\) (izotop helija): \begin{matrix} \begin{align*} &_{1}^{2}\textrm{H}+_{1}^{2}\textrm{H}\rightarrow _{2}^{3}\textrm{He}+_{0}^{1}\textrm{n}\,\qquad Q=3,27\,\textrm{MeV}\\ &_{1}^{2}\textrm{H}+_{1}^{2}\textrm{H}\rightarrow _{1}^{3}\textrm{H}+_{1}^{1}\textrm{p}\,\,\,\,\qquad Q=4,03\,\textrm{MeV}\\ &_{1}^{2}\textrm{H}+_{1}^{3}\textrm{H}\rightarrow _{2}^{4}\textrm{He}+_{0}^{1}\textrm{n}\,\,\qquad Q=17,6\,\textrm{MeV}\\ &_{1}^{2}\textrm{H}+_{2}^{3}\textrm{He}\rightarrow _{2}^{4}\textrm{He}+_{1}^{1}\textrm{p}\qquad Q=18,3\,\textrm{MeV} \end{align*} \end{matrix} Jezgra atoma deuterija zove se deuteron, a jezgra tricija zove se triton.
Točan odgovor je A.
23. zadatak
Opažač na Zemlji opazi svemirsku letjelicu i izmjeri da joj je duljina 1 km kada se približava Zemlji brzinom 0,6c.
Koliku duljinu letjelice mjeri kapetan koji se u njoj nalazi?
- A. 600 m
- B. 800 m
- C. 1000 m
- D. 1250 m
Kontrakcija duljine: \[L=L_{0}\sqrt{1-\frac{v^{2}}{c^{2}}}\]
- \(L_{0}\) - duljina rakete u smjeru gibanja koju mjeri putnik u raketi (putnik u raketi miruje)
- \(L\) - duljina rakete u smjeru gibanja koju mjeri promatrač u odnosu na kojega se raketa giba brzinom \(v\)
- \(c\) - brzina svjetlosti
\[L=1000\,\textrm{m}\] \[L_{0}=\frac{L}{\sqrt{1-v^{2}/c^{2}}}=1250\,\textrm{m}\]
24. zadatak
Kolika je procijenjena starost svemira prema teoriji velikoga praska?
- A. oko 4 milijuna godina
- B. oko 14 milijuna godina
- C. oko 4 milijarde godina
- D. oko 14 milijardi godina
Svemir je nastao prije 13,8 milijardi godina u događaju kojega nazivamo veliki prasak (Big Bang).
25. zadatak
Idealni plin početne temperature \(20\,^{\circ}\textrm{C}\) izohorno se zagrije na temperaturu \(606\,^{\circ}\textrm{C}\) i pritom mu se tlak poveća
za 100 kPa.
Koliko iznosi početni tlak plina?
Odgovor: kPa
Izohorna promjena stanja plina (volumen plina je konstantan): \[\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\]
\[\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\] \[P_{1}=P_{2}\,\frac{T_{1}}{T_{2}}\] \[P_{2}=P_{1}+100\,\textrm{kPa}\] \[P_{1}=\left(P_{1}+100\,\textrm{kPa}\right)\cdot\frac{293}{879}\] \[P_{1}=\left(P_{1}+100\,\textrm{kPa}\right)\cdot\frac{1}{3}\] \[3\,P_{1}=P_{1}+100\,\textrm{kPa}\] \[2\,P_{1}=100\,\textrm{kPa}\] \[P_{1}=50\,\textrm{kPa}\]
26. zadatak
Na slici je prikazan val koji put od točke A do točke B prijeđe za 1,5 s.
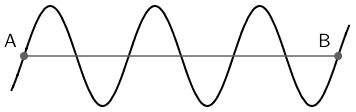
Kolika je frekvencija vala?
Odgovor: Hz
Frekvencija vala jednaka je frekvenciji titranja izvora vala: \[f=\frac{n}{t}\]
- \(n\) - broj titraja izvora vala za vrijeme \(t\)
Frekvenciju titranja izvora možemo odrediti i kao recipročnu vrijednost perioda titranja izvora: \[f=\frac{1}{T}\]
Valna duljina jednaka je udaljenosti koju prijeđe val za vrijeme dok izvor vala izvrši jedan puni titraj. Iz slike vidimo da je izvor vala izvršio \(n=3\) puna titraja za vrijeme \(t=1,5\,\textrm{s}\). \[f=\frac{n}{t}=\frac{3}{1,5}=2\,\textrm{Hz}\]
27. zadatak
Splav napravljena od drva gustoće 800 kg/m3 nalazi se na površini vode. U vodu se polako dodaje sol tako da joj gustoća naraste za 10 %.
Gustoća vode iznosi 1000 kg/m3.
Za koliko se posto smanji uronjeni dio volumena splavi u odnosu na ukupan volumen splavi?
Odgovor: %
Uzgon je sila koja djeluje na tijelo uronjeno u fluid i koja je suprotno orijentirana od sile teže: \[F_{\textrm{u}}=\rho g V_{\textrm{udt}}\]
- \(\rho\) - gustoća fluida (u ovom zadatku je to gustoća vode)
- \(V_{\textrm{udt}}\) - volumen uronjenog dijela tijela
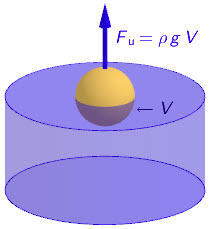
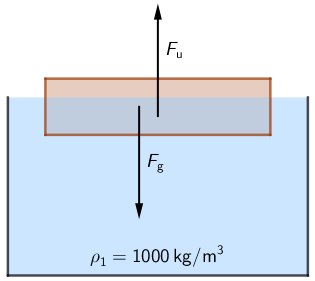
Na dasku djeluju sila teža i sila uzgona. Te dvije sile imaju jednak iznos jer daska miruje. \[F_{\textrm{u}}=\rho_{1}\,g\,V_{1}\]
- \(\rho_{1}=1000\,\textrm{kg/m}^{3}\) - gustoća vode
- \(V_{1}\) - volumen uronjenog dijela daske
- \(\rho_{\textrm{d}}=800\,\textrm{kg/m}^{3}\) - gustoća drvene daske
- \(V\) - volumen daske
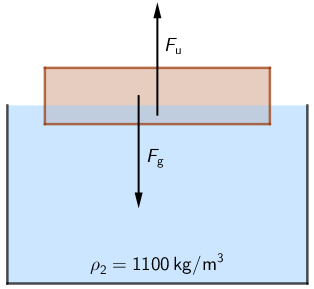
\[F_{\textrm{u}}=F_{\textrm{g}}\] \[F_{\textrm{u}}=\rho_{2}\,g\,V_{2}\]
- \(\rho_{2}=1100\,\textrm{kg/m}^{3}\) - gustoća vode kojoj smo dodali sol
- \(V_{2}\) - volumen uronjenog dijela daske
\[\rho_{2}\,g\,V_{2}=\rho_{\textrm{d}}\,V\,g\] \[V_{2}=\frac{\rho_{\textrm{d}}}{\rho_{2}}\,V=0,727\,V\] Smanjenje volumena: \[\Delta V=V_{2}-V_{1}=0,073\,V\] Smanjenje volumena u postocima u odnosu na volumen daske: \[\frac{\Delta V}{V}\cdot 100=7,3\,\%\]
28. zadatak
Na slici je prikazan kružni termodinamički proces u p,V koordinatnom sustavu. Od točke A do točke B idealni plin duž izoterme obavlja rad nad okolinom iznosa 5 J. Od točke B do točke C plin duž adijabate obavlja rad nad okolinom iznosa 3 J.
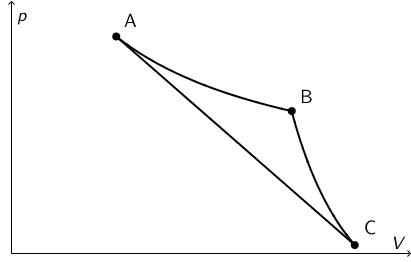
Kolika je promjena unutarnje energije plina u izotermnome procesu \(\Delta U_{\textrm{AB}}\), a kolika u adijabatskome procesu \(\Delta U_{\textrm{BC}}\)?
\(\Delta U_{\textrm{AB}}\) = J
\(\Delta U_{\textrm{BC}}\) = J
Unutarnja energija termodinamičkog sustava može se mijenjati pomoću topline koju sustav izmjenjuje s okolinom i pomoću rada kojeg sustav obavlja nad okolinom ili okolina obavlja nad sustavom.
- \(Q\) - toplina koju sustav razmjenuje s okolinom
- \(W\) - rad kojeg sustav obavlja nad okolinom ili okolina obavlja nad sustavom
- \(\Delta U=U_{2}-U_{1}\) - promjena unutarnje energije sustava (razlika unutarnjih energija u konačnom i početnom stanju)
Primijenimo zakon očuvanja energije. Promjena unutarnje energije zatvorenog sustava jednaka je razlici energije koju sustav prima zagrijavanjem i
rada kojeg sustav obavlja nad okolinom.
\[\Delta U= Q - W\]
Ovo je matematički zapis općeg zakona o očuvanju energije, pri čemu su uključeni unutarnja energija, toplina i mehanički rad, a nazivamo ga
prvi zakon termodinamike.
Prvi zakon termodinamike zapisujemo i u obliku:
\[Q = W + \Delta U\]
Toplina dovedena sustavu pretvara se u mehanički rad i promjenu unutarnje energije.
U termodinamičkom sustavu energija ne može nastati ni nestati sama po sebi. Energija može prelaziti iz jednog oblika u drugi.
Primijenimo prvi zakon termodinamike na termodinamičke procese kroz koje prolazi idealni plin.
Promjena unutarnje energije idealnog plina jednaka je:
\begin{matrix}
\begin{align*}
&\Delta U=U_{2}-U_{1}\\
&\Delta U=\frac{i}{2}n\,R\,T_{2}-\frac{i}{2}n\,R\,T_{1}\\
&\Delta U=\frac{i}{2}n\,R\,\left(T_{2}-T_{1} \right)\\
&\Delta U=\frac{i}{2}n\,R\,\Delta T
\end{align*}
\end{matrix}
- \(i=3\) za jednoatomni idealni plin
- \(i=5\) za dvoatomni idealni plin
- Izotermni proces: \(T=\textrm{konst.}\) proces u kojemu se ne mijenja temperatura plina
- Adijabatski proces: \(Q=0\) proces u kojemu nema izmjene topline između plina i okoline
Proces A-B:
Temperatura je konstantna. Promjena unutarnje energije:
\[\Delta U_{\textrm{AB}}=\frac{i}{2}n\,R\,\Delta T = 0\]
Proces B-C:
Nema izmjene topline između plina i okoline:
\[Q=0\]
Na osnovu prvog zakona termodinamike:
\[\Delta U= Q - W\]
zaključujemo:
\[\Delta U_{\textrm{BC}}=- W=-3\,\textrm{J}\]
Pri adijabatskom širenju plin obavlja rad na račun svoje unutarnje energije pa se ona zbog toga smanjuje.
Pri adijabatskom sabijanju okolina obavlja rad pa se unutarnja energija povećava.
29. zadatak
Pozitivni naboj iznosa 20 nC i mase 50 g nalazi se u homogenome električnom polju ovješen na
nit duljine \(\ell\). Električno polje iznosa 2,5 MV/m usmjereno je vertikalno prema gore. Naboj se nalazi u zraku. Sila uzgona
je zanemariva.
Koliki je iznos napetosti niti na koju je ovješen naboj?
Odgovor: N
Na električni naboj u homogenom električnom polju djeluju sila teža i električna sila.
Kako su te sile orijentirane?
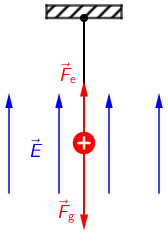
Na električni naboj \(q=20\,\textrm{C}\) i mase \(m=50\,\textrm{g}\) djeluju sila teža \(F_{\textrm{g}}=m\,g\) i električna sila \(F_{\textrm{e}}=q\,E\):
Napetost niti \(N\) iznosi:
\[N=F_{\textrm{g}}-F_{\textrm{e}}\]
\[N=m\,g-qE=0,45\,\textrm{N}\]
30. zadatak
Koliko fotona u sekundi emitira laser valne duljine 600 nm i snage 1 W?
Odgovor:
Energija jednog fotona: \[E_{\textrm{f}}=h\,f=\frac{h\,c}{\lambda}\] Energija \(N\) fotona: \[E=N\,E_{\textrm{f}}\] Snaga lasera: \[P=\frac{E}{t}\]
\[E_{\textrm{f}}=h\,f=\frac{h\,c}{\lambda}=3,32\cdot 10^{-19}\,\textrm{J}\] \[P=\frac{E}{t}=\frac{N\,E_{\textrm{f}}}{t}\] \[N=\frac{P\,t}{E_{\textrm{f}}}=3\cdot 10^{18}\]
31. zadatak
Projektil mase m = 8 kg ispuca se vertikalno prema gore brzinom 10 m/s.
U najvišoj točki svoje putanje eksplodira na dva komada od kojih jedan ima masu 3 kg i poleti brzinom
5 m/s vertikalno prema gore. Otpor zraka je zanemariv.
Kojom brzinom drugi dio projektila udari u tlo?
Odgovor: m/s
- Kolika je maksimalna visina koju postigne projektil? Ako ne znate gotov izraz, primijenite zakon očuvanja mehaničke energije.
- U najvišoj točki kugla se raspadne na dva dijela. Primijenite zakon očuvanja količine gibanja kako biste odredili brzinu većeg dijela projektila.
- Kolikom brzinom veći dio projektila padne na tlo? Ako ne znate gotov izraz, primijenite zakon očuvanja mehaničke energije.
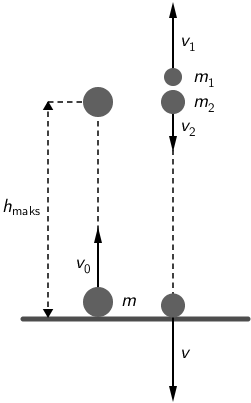
Mehanička energija projektila u trenutku izbacivanja jednaka je njegovoj kinetičkoj energiji: \[E_{1}=\frac{1}{2}m\,v_{0}^{2}\] U trenutku kada projektil dostigne najvišu točku, na trenutak zastane pa mu je kinetička energija jednaka nuli. Mehanička energija tada je jednaka njegovoj gravitacijskoj potencijalnoj energiji: \[E_{2}=m\,g\,h_{\textrm{maks}}\] Primijenimo zakon očuvanja mehaničke energije: \[E_{1}=E_{2}\] \[\frac{1}{2}m\,v_{0}^{2}=m\,g\,h_{\textrm{maks}}\] Maksimalna visina do koje se projektil podigne je: \[h_{\textrm{maks}}=\frac{v_{0}^{2}}{2\,g}=5\,\textrm{m/s}\] Primijenimo zakon očuvanja količine gibanja. U najvišoj točki, neposredno prije nego se projektil raspadne, količina gibanja jednaka je nuli jer se projektil na trenutak zaustavio: \[0=m_{1}\,v_{1}-m_{2}\,v_{2}\] \[v_{2}=\frac{m_{1}}{m_{2}}\cdot v_{1}=3\,\textrm{m/s}\] Ukupna mehanička energija u tom trenutku jednaka je zbroju kinetičke i gravitacijske potencijalne energije projektila: \[E_{3}=\frac{1}{2}m_{2}\,v_{2}^{2}+m_{2}\,g\,h_{\textrm{maks}}\] U trenutku kada veći dio projektila mase \(m_{2}=5\,\textrm{kg}\) padne na tlo, njegova je energija jednaka kinetičkoj energiji u trenutku pada: \[E_{4}=\frac{1}{2}m_{2}\,v^{2}\] Primijenimo zakon očuvanja mehaničke energije: \[E_{3}=E_{4}\] \[\frac{1}{2}\,m_{2}\,v_{2}^{2}+m_{2}\,g\,h_{\textrm{maks}}=\frac{1}{2}\,m_{2}\,v^{2}\] \[v^{2}=v_{2}^{2}+2\,g\,h_{\textrm{maks}}\] \[v=\sqrt{v_{2}^{2}+2\,g\,h_{\textrm{maks}}}=10,44\,\textrm{m/s}\]
32. zadatak
Skijaš mase 80 kg spušta se niz stazu nagnutu pod kutom \(30^{\circ}\) u odnosu na horizontalu.
Otpor zraka na skijaša iznosi 20 N, a faktor trenja između skija i snježne podloge iznosi 0,08.
Koliko iznosi ubrzanje skijaša niz stazu?
Odgovor: \(\textrm{m/s}^{2}\)
- Koje sile djeluju na skijaša?
- Odredite rezultantu svih sila koje djeluju na skijaša.
- Primijenite temeljni zakon gibanja.
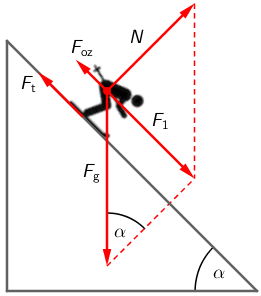
Na skijaša djeluju:
- Sila teža \(F_{\textrm{g}}\)
- Reakcija podloge (sila kojom podloga djeluje na skijaša) \(N\)
- Sila trenja \(F_{\textrm{t}}\)
- Sila otpora zraka \(F_{\textrm{oz}}\)
Rezultanta sila \(F_{\textrm{g}}\) i \(N\), koja je na slici označena s \(F_{1}\), vuče skijaša prema dnu kosine: \[F_{1}=F_{\textrm{g}}\,\textrm{sin}\,\alpha\] \[F_{1}=m\,g\,\textrm{sin}\,\alpha\] \[F_{1}=\frac{m\,g}{2}=400\,\textrm{N}\] \[N=F_{\textrm{g}}\,\textrm{cos}\,\alpha\] \[N=m\,g\,\textrm{cos}\,\alpha=692,82\,\textrm{N}\] \[F_{\textrm{t}}=\mu\,N=55,43\,\textrm{N}\] Iz slike vidimo da je rezultanta svih sila koje djeluju na skijaša jednaka: \[F=F_{1}-\left(F_{\textrm{t}}+F_{\textrm{oz}}\right)=324,57\,\textrm{N}\] Akceleraciju skijaša odredimo pomoću drugog Newtonovog zakona: \[a=\frac{F}{m}=4,06\,\textrm{m/s}^{2}\]
33. zadatak
Ion argona naboja \(1,6\cdot 10^{−19}\,\textrm{C}\) ubrzan je u električnome polju razlikom potencijala 900 V iz mirovanja.
Nakon što se ubrza, ion ulijeće okomito na silnice homogenoga magnetskog polja iznosa 400 mT i giba se po kružnoj putanji
polumjera 7,5 cm.
Kolika je masa iona argona?
Odgovor: kg
Rad kojeg obavi električno polje pretvori se u kinetičku energiju elektrona.
Kada elektron uleti okomito na homogeno magnetsko polje, na njega
djeluje Lorentzova sila:
\[F_{\small{\textrm{L}}}=e\,v\,B\]
Lorentzova sila ima ulogu centripetalne sile zbog čega se u magnetskom polju elektron giba jednoliko po kružnici.
Rad kojeg obavi električno polje: \[W=e\,U\] Kinetička energija elektrona: \[E_{\textrm{k}}=\frac{1}{2}\,m\,v^{2}\] \[E_{\textrm{k}}=W\] \[\frac{1}{2}\,m\,v^{2}=e\,U\qquad(1)\] Ulogu centripetalne sile \[F_{\textrm{cp}}=\frac{m\,v^{2}}{r}\] ima Lorentzova sila \[F_{\small{\textrm{L}}}=e\,v\,B\] \[F_{\textrm{cp}}=F_{\small{\textrm{L}}}\] \[e\,v\,B=\frac{m\,v^{2}}{r}\] \[v=\frac{e\,B\,r}{m}\] Ovaj izraz za brzinu uvrstimo u izraz (1): \[\frac{m}{2}\cdot \frac{e^{2}\,B^{2}\,r^{2}}{m^{2}}=e\,U\] \[m=\frac{e\,B^{2}\,r^{2}}{2\,U}\] \[m=8\cdot 10^{-26}\,\textrm{kg}\]
34. zadatak
Tijelo mase 20 g harmonijski titra na elastičnoj opruzi periodom 0,51 s.
Amplituda titranja je 15 cm.
Kolika je kinetička energija tijela u trenutku kada je ono udaljeno 5 cm od ravnotežnoga položaja?
Odgovor: J
Ukupna mehanička energija harmonijskog titranja u nekom trenutku jednaka je zbroju elastične potencijalne energije i kinetičke energije: \[E=E_{\textrm{ep}}+E_{\textrm{k}}\] \[E=\frac{1}{2}\,k\,x^{2}+\frac{1}{2}\,m\,v^{2}\] Kada se tijelo nalazi u amplitudnom položaju ukupna mehanička energija jednaka je maksimalnoj elastičnoj potencijalnoj energiji: \[E=\frac{1}{2}\,k\,A^{2}\] Kada se tijelo nalazi u ravnotežnom položaju ukupna mehanička energija jednaka je maksimalnoj kinetičkoj energiji: \[E=\frac{1}{2}\,m\,v_{0}^{2}\]
Odredimo harmonijsku konstantu ovog titranja: \[k=m\,\omega^{2}\] \[k=m\,\left(\frac{2\,\pi}{T}\right)^{2}=3,04\,\textrm{N/m}\] Ukupna energija jednaka je maksimalnoj elastičnoj potencijalnoj energiji: \[E=\frac{1}{2}\,k\,A^{2}\] \[E=0,034\,\textrm{J}\] Elastična potencijalna energija u trenutku kada je elongacija titranja tijela x = 5 cm: \[E_{\textrm{ep}}=\frac{1}{2}\,k\,x^{2}=3,8\cdot 10^{-3}\,\textrm{J}\] \[E_{\textrm{k}}=E-E_{\textrm{ep}}=0,03\,\textrm{J}\]
35. zadatak
Učenik treba odrediti unutarnji otpor izvora. Na raspolaganju ima dva otpornika različitih otpora \(R_{1}\) i \(R_{2}\), prekidač, voltmetre i ampermetre te izvor stalnoga napona. Na slici je prikazan jedan od načina spajanja strujnoga kruga.
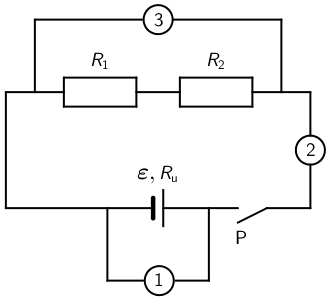
35.1. Učenik mora ispravno izmjeriti elektromotorni napon izvora. Navedeni su mogući položaji na koje učenik može spojiti voltmetar.
- Položaj 1 uz otvoreni prekidač
- Položaj 2 uz otvoreni prekidač
- Položaj 3 uz otvoreni prekidač
- Položaj 1 uz zatvoreni prekidač
- Položaj 2 uz zatvoreni prekidač
- Položaj 3 uz zatvoreni prekidač
U polje za unos napišite redni broj iskaza kojim učenik može ispravno izmjeriti elektromotorni napon izvora.
Redni broj iskaza:
35.2. Učenik je napravio nekoliko mjerenja. Prvo je spojio svaki otpornik pojedinačno u strujni krug i očitao vrijednosti na mjernim instrumentima, a potom je otpornike spojio u seriju pa u paralelu i ponovno očitao vrijednosti na mjernim instrumentima. Mjerenja je prikazao \(U,I\) grafom kao što je prikazano na slici.
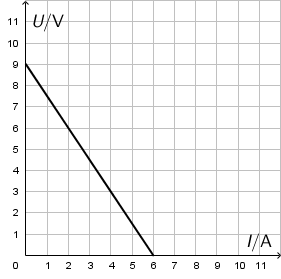
Koliki je elektromotorni napon izvora?
\(\large\varepsilon\) = V
35.3. Koliki je unutarnji otpor izvora?
\(R_{\textrm{u}}\) = \(\Omega\)
35.1.
Voltmetar se spaja paralelno s izvorom struje dok je strujni krug otvoren.
35.2.
Voltmetar se spaja paralelno s izvorom struje dok je strujni krug otvoren. Dok je strujni krug otvoren, kroz njega struja ne prolazi. Iz \(U,I\) grafa vidimo da struji od 0 A odgovara napon od 9 V.
35.3.
Unutarnji otpor moguće je odrediti tako da polove izvora struje kratko spojimo. Primijenimo Ohmov zakon za cijeli strujni krug:
\[I=\frac{\large{\varepsilon}}{R_{\textrm{u}}+R_{\textrm{v}}}\]
Kada polove izvora struje kratko spojimo vanjski otpor jednak je nuli
\[R_{\textrm{v}}=0\]
\[I=\frac{\large\varepsilon}{R_{\textrm{u}}}\]
Struju kratkog spoja očitamo iz grafa kao najveću vrijednost struje
\[I_{\textrm{ks}}=6\,\textrm{A}\]
\[R_{\textrm{u}}=\frac{\large{\varepsilon}}{I_{\textrm{ks}}}=1,5\,\Omega\]