Ljetni rok 2014. godine
1. zadatak
Elastična opruga produlji se za 0,1 m zbog djelovanja sile iznosa 15 N.
Koliko iznosi konstanta elastičnosti te opruge?
- A. \(0,15\, \textrm{N}/\textrm{m}\)
- B. \(1,5\, \textrm{N}/\textrm{m}\)
- C. \(15\, \textrm{N}/\textrm{m}\)
- D. \(150\, \textrm{N}/\textrm{m}\)
Kako ovisi elastična sila o produljenju opruge? Kojom se formulom može prikazati?
Elastična sila \(F_{\textrm{el}}\) proporcionalna je produljenju \(x\): \(F_{\textrm{el}}=kx\). Iz ovog izraza za konstantu elastičnosti dobijemo \[k=\frac{F_{\textrm{el}}}{x}=150\,\textrm{N/m}\]
2. zadatak
Na kvadar koji se nalazi na vodoravnoj podlozi djeluje sila iznosa 3 N. Sila je usporedna s podlogom.
Kvadar se giba jednoliko u smjeru djelovanja sile.
Što je od navedenoga točno za iznos sile trenja \(F_{\textrm{tr}}\) između kvadra i podloge?
- A. \(F_{\textrm{tr}}=0\,\textrm{N}\)
- B. \(0\,\textrm{N} < F_{\textrm{tr}} < 3\,\textrm{N}\)
- C. \(F_{\textrm{tr}}=3\,\textrm{N}\)
- D. \(3\,\textrm{N} < F_{\textrm{tr}}\)
Primijenite prvi Newtonov zakon.
Budući da se kvadar giba jednoliko, ukupna sila na njega mora biti jednaka nuli, pa zaključiujemo da je sila trenja suprotno orijentirana i ima jednak iznos kao i sila \(F\): \[F_{\textrm{tr}}=3\,\textrm{N}\]

3. zadatak
Tijelo je bačeno vodoravno s neke visine.
Koji od ponuđenih grafova prikazuje iznos vodoravne komponente brzine tijela u ovisnosti o vremenu tijekom pada?
Zanemarite otpor zraka.
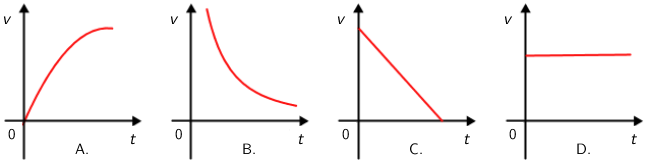
- A. Graf A
- B. Graf B
- C. Graf C
- D. Graf D
Horizontalni hitac je složeno gibanje. Od kojih se jednostavnih gibanja sastoji? Kako se mijenjaju njihove brzine?
Horizontalni hitac sastoji se od jednolikog gibanja po horizontalnom pravcu i slobodnog pada po vertikalnom pravcu. Brzina jednolikog gibanja po horizontalnom pravcu ne mijenja se. Graf D. prikazuje gibanje tijela konstantnom brzinom.
4. zadatak
Period kruženja umjetnoga satelita oko planeta iznosi \(T\). Udaljenost satelita od središta planeta iznosi \(r\).
Na kolikoj udaljenosti od središta planeta kruži drugi satelit kojemu je period kruženja \(T/8\)?
- A. \(r/8\)
- B. \(r/4\)
- C. \(4\,r\)
- D. \(8\,r\)
Primijenite treći Keplerov zakon na sustav planeta oko kojega kruže dva satelita.
Treći Keplerov zakon:
Kvadrati ophodnih vremena satelita odnose se kao kubovi njihovih srednjih udaljenosti od planeta.
\[\left(T:\frac{T}{8}\right)^{2}=\left(r:r_{2}\right)^{3}\]
\[\left(\frac{r}{r_{2}}\right)^{3}=64\]
\[r_{2}=\frac{r}{\sqrt[3]{64}}=\frac{r}{4}\]
5. zadatak
Tijelo oblika kocke cijelo je uronjeno u tekućinu kao što je prikazano na crtežu. Pritom su dvije stranice tijela vodoravne. Hidrostatski tlak u točki A je \(p_{\small{\textrm{A}}}\), u točki B je \(p_{\small{\textrm{B}}}\), u točki C je \(p_{\small{\textrm{C}}}\) , a u točki D je \(p_{\small{\textrm{D}}}\).
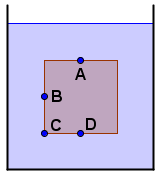
Što od navedenoga vrijedi za te hidrostatske tlakove?
- A. \(p_{\small{\textrm{A}}} < p_{\small{\textrm{B}}} < p_{\small{\textrm{C}}} < p_{\small{\textrm{D}}}\)
- B. \(p_{\small{\textrm{A}}} < p_{\small{\textrm{B}}} < p_{\small{\textrm{C}}} = p_{\small{\textrm{D}}}\)
- C. \(p_{\small{\textrm{A}}} < p_{\small{\textrm{B}}} = p_{\small{\textrm{C}}} < p_{\small{\textrm{D}}}\)
- D. \(p_{\small{\textrm{A}}} = p_{\small{\textrm{D}}} < p_{\small{\textrm{B}}} = p_{\small{\textrm{C}}}\)
O čemu ovisi i kojim se izrazom može prikazati hidrostatski tlak u tekućini?
Hidrostatski tlak na neku točku u tekućini ovisi o gustoći tekućine \(\rho\), akceleraciji sile teže \(g\) i dubini na kojoj se točka nalazi, \(h\). (udaljenost od površine tekućine) \[p=\rho g h\] Na crtežu vidimo da se na najmanjoj dubini nalazi točka A, zatim točka B pa onda točke C i D. Tako se onda odnose i pripadni hidrostatski tlakovi.
6. zadatak
Određena se količina vode zagrijava u zatvorenoj posudi. Pritom je cjelokupna količina vode u tekućemu stanju.
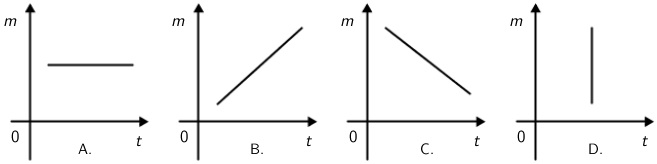
Koji od ponuđenih crteža prikazuje masu vode u ovisnosti o temperaturi tijekom grijanja?
- A. Crtež A
- B. Crtež B
- C. Crtež C
- D. Crtež D
Voda se nalazi u zatvorenoj posudi.
Ako vodu zagrijavamo u zatvorenoj posudi njezina se masa ne mijenja.
7. zadatak
Tijekom promjene stanja plin gubi toplinu od 100 J, a u isto vrijeme obavlja rad od 20 J.
Što je od navedenoga točno za unutarnju energiju toga plina?
- A. Smanjila se za 120 J
- B. Smanjila se za 80 J
- C. Povećala se za 80
- D. Povećala se za 120 J
Primijenite prvi zakon termodinamike.
Toplina je energija i ako ju dovodimo sustavu (npr. plin u posudi s pomičnim klipom) ona može povećati unutarnju energiju sustava ili omogućiti sustavu da vrši rad. To je opći zakon očuvanja energije. Nazivamo ga i prvi zakon termodinamike. \[\Delta Q=W+\Delta U\] Često se prvi zakon termodinamike zapisuje i ovako: \[\Delta U= \Delta Q-W\] Unutarnju energiju sustava možemo mijenjati dovođenjem ili odvođenjem topline i vršenjem rada.
U primjeru iz zadatka plin predaje toplinu pa je ona negativna: \(\Delta Q = - 100\,\textrm{J}\). Plin vrši rad pa je on pozitivan: \(W=20\, \textrm{J}\). Ako ove podatke uvrstimo u prvi zakon termodinamike, dobivamo: \[\Delta U= \Delta Q-W=-100 - 20 = - 120\, \textrm{J}\]
8. zadatak
Električki neutralno tijelo nakon trljanja vunenom krpom postane elektrizirano nabojem \(+Q\).
Koliki je ukupan naboj krpe i tijela nakon trljanja? Vunena krpa bila je električki neutralna prije trljanja.
- A. \(-Q\)
- B. \(0\)
- C. \(+Q\)
- D. \(+2\,Q\)
Primijenite zakon očuvanja električnog naboja.
Ukupan električni naboj krpe i tijela prije trljanja bio je jednak nuli. Prema zakonu očuvanja električnog naboja, toliki mora biti i
nakon trljanja.
Iako je nakon trljanja naboj tijela \(+Q\), ne treba zaboraviti da je naboj krpe \(-Q\) pa je ukupni naboj jednak nuli.
9. zadatak
Promjenjivi otpornik spojen je na izvor elektromotornoga napona \(\large{\varepsilon}\) i unutarnjega otpora \(R_{\textrm{u}}\). Graf prikazuje napon na
promjenjivome otporniku u ovisnosti o struji koja prolazi kroz taj otpornik.
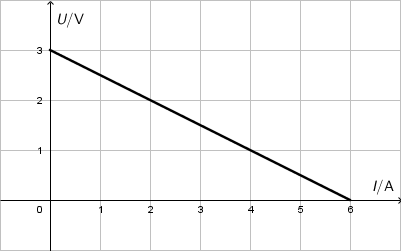
Koliko iznosi struja kratkoga spoja?
- A. 3 A
- B. 6 A
- C. 9 A
- D. 18 A
Primijenite Ohmov zakon za cijeli strujni krug. Što je struja kratkoga spoja?
Iz Ohmova zakona za cijeli strujni krug: \[I=\frac{\large{\varepsilon}}{R+R_{\textrm{u}}}\] vidimo da je struja koja prolazi krugom maksimalna ako je vanjski otpor \(R\) jednak nuli. Tu struju nazivamo strujom kratkog spoja. Iz zadanog grafa vidimo da maksimalna struja iznosi \(6\,\textrm{A}\).
10. zadatak
Na crtežu je prikazan dio strujnoga kruga. Omjer otpora je \(R_{1}:R_{2}:R_{3}=1:2:4\). Struja koja prolazi kroz otpornik \(R_{3}\) iznosi 3 A.
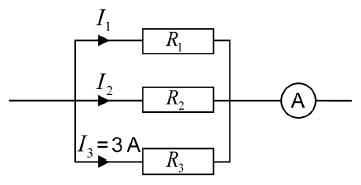
Koliku struju pokazuje ampermetar A?
- A. 3 A
- B. 6 A
- C. 12 A
- D. 21 A
Što znamo o naponima na paralelno spojenim otporima? Odredite struje kroz prva dva otpora i primijenite prvo Kirchhoffovo pravilo.
Otpori su spojeni paralelno pa su naponi na njima jednaki: \[U_{1}=U_{2}=U_{3}\] Na svaki od tih otpora primijenimo Ohmov zakon za dio strujnog kruga: \[I_{1}\,R_{1}=I_{2}\,R_{2}=I_{3}\,R_{3}\] Iz drugog i trećeg člana dobijemo: \[I_{2}=\frac{I_{3}\,R_{3}}{R_{2}}=3\,\cdot \frac{4}{2}=6\,\textrm{A}\] Iz prvog i trećeg člana dobivamo: \[I_{1}=\frac{I_{3}\,R_{3}}{R_{1}}=3\,\cdot \frac{4}{1}=12\,\textrm{A}\] Na osnovu prvog Kirchhoffovog pravila ampermetar će prikazivati struju: \[I=I_{1}+I_{2}+I_{3}=3+6+12=21\,\textrm{A}\]
11. zadatak
Otpornik otpora \(100\,\Omega\) spojen je u krug izmjenične struje. Graf prikazuje struju koja prolazi kroz otpornik u ovisnosti o vremenu.
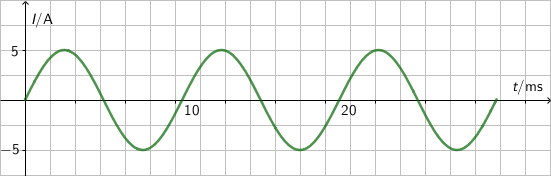
Koliki je maksimalni napon na otporniku?
- A. \(5\,\textrm{V}\)
- B. \(10\,\textrm{V}\)
- C. \(50\,\textrm{V}\)
- D. \(500\,\textrm{V}\)
Kolika je maksimalna struja kroz otpornik? Primijenite Ohmov zakon.
Iz grafa čitamo da je maksimalna struja: \[I_{0}=5\,\textrm{A}\] Na osnovu Ohmovog zakona maksimalni napon iznosi: \[U_{0}=I_{0}\,R=500\,\textrm{V}\]
12. zadatak
Tijelo harmonijski titra. Elongacija tijela u ovisnosti o vremenu opisana je izrazom
\[y=2\,\textrm{m}\cdot \textrm{sin}\left ( \frac{\pi\,t}{3\,\textrm{s}}\right )\]
Koliki je period titranja toga tijela?
- A. 2/3 s
- B. 3/2 s
- C. 3 s
- D. 6 s
Napišite jednadžbu za harmonijsko titranje i usporedite ju sa zadanom jednadžbom.
Jednadžbu harmonijskog titranja \[y=y_{0}\,\textrm{sin}\left ( 2\pi\frac{t}{T}+\varphi_{0} \right )\] usporedimo s jednadžbom titranja iz zadatka \[y=2\,\textrm{m}\cdot \textrm{sin}\left ( \frac{\pi\,t}{3\,\textrm{s}}\right )\] Izjednačimo članove u zagradama koji sadrže vrijeme \[\frac{\pi\,t}{3\,\textrm{s}}=2\pi\frac{t}{T}\] Rješenje ove jednadžbe je \[T=6\,\textrm{s}\]
13. zadatak
Otvoreni \(\textrm{LC}\) krug emitira elektromagnetski val valne duljine \(\lambda_{0}\). Ako se kapacitet u tome \(\textrm{LC}\) krugu smanji na devetinu početne vrijednosti, krug emitira elektromagnetski val valne duljine \(\lambda\).
Koliki je omjer valnih duljina \(\lambda/\lambda_{0}\)
- A. 1/9
- B. 1/3
- C. 3
- D. 9
Kako valna duljina elektromagnetskog vala ovisi o njegovoj brzini i o periodu titranja \(\textrm{LC}\) kruga? Kako se može prikazati period titranja \(\textrm{LC}\) kruga?
Valna duljina elektromagnetskog vala može se prikazati kao \(\lambda=c\cdot T\), gdje je \(T\) period elektromagnetskih titraja titrajnoga \(\textrm{LC}\) kruga: \[T=2\pi\sqrt{LC}\] Neka su početna valjna duljina i period \[\lambda_{0}=c\cdot T_{0}\] \[T_{0}=2\pi\sqrt{LC_{0}}\] Konačne vrijednosti: \[\lambda=c\cdot T\] \[T=2\pi\sqrt{LC}\] Konačni kapacitet je \(C=C_{0}/9\). Za omjer valnih duljina dobivamo: \[\frac{\lambda}{\lambda_{0}}=\sqrt\frac{C}{C_{0}}=\frac{1}{3}\]
14. zadatak
Koliko je daleko od promatrača eksplodirala raketa vatrometa ako je promatrač vidio njezin bljesak 2 s prije nego što je čuo
zvuk eksplozije?
Brzina zvuka u zraku iznosi 340 m/s i puno je manja od brzine svjetlosti.
- A. 170 m
- B. 340 m
- C. 680 m
- D. 1360 m
Koliko je vremena potrebno svjetlosti i zvuku da stignu do promatrača? Uzmite u obzir da zvuk putuje dvije sekunde dulje.
Vrijeme potrebno svjetlosti da stigne do promatrača:
\[t_{\textrm{sv}}=\frac{s}{c}\]
Vrijeme potrebno zvuku da stigne do promatrača:
\[t_{\textrm{zv}}=\frac{s}{v}\]
Iz ove dvije jednadžbe dobijemo:
\[\frac{t_{\textrm{sv}}}{t_{\textrm{zv}}}=\frac{v}{c}\ll 1\]
Brzina svjetlosti puno je veća od brzine zvuka, pa možemo pretpostaviti da svjetlost do promatrača stigne "trenutno" (\(t_{\textrm{sv}}\approx 0\)).
Udaljenost promatrača od mjesta eksplozije jednaka je:
\[s=v\cdot t_{\textrm{zv}}=680\,\textrm{m}\]
15. zadatak
Divergentna leća ima žarišnu daljinu \(f\). Predmet se nalazi na udaljenosti \(2f\) od središta leće. Oštra slika predmeta vidi se na
udaljenosti \(d\) od središta leće.
Koliko iznosi \(d\)?
- A. \(2f/3\)
- B. \(f\)
- C. \(3f/2\)
- D. \(2f\)
Napišite jednadžbu leće. Pripazite na predznake za slučaj divergentne leće.
Jednadžba leće je \[\frac{1}{a}+\frac{1}{b}=\frac{1}{f}\] Iz jednadžbe leće za udaljenost oštre slike dobivamo: \[\frac{1}{b}=\frac{1}{f}-\frac{1}{a}\Rightarrow b=\frac {f\,a}{a-f}\] Žarišna daljina divergentne leće je negativna \[f < 0\] Udaljenost realnog predmeta je \[a=2\,f\] Udaljenost virtualne slike je negativna: \[b < 0 \Rightarrow b=-d\] Za udaljenost \(d\) dobivamo \[-d=\frac {f\,a}{a-f}=\frac{-f\cdot 2f}{2f+f}=\frac{-2\,f^{2}}{3\,f}=-\frac{2\,f}{3}\] \[d=\frac{2\,f}{3}\]
16. zadatak
Dva snopa svjetlosti destruktivno interferiraju u točki T.
Za koliko se razlikuju prijeđeni putovi tih dvaju snopova do točke T?
- A. za paran broj valnih duljina
- B. za neparan broj valnih duljina
- C. za neparan broj polovina valne duljine
- D. za paran broj polovina valne duljine
Koji je uvjet da se bilo koja dva vala interferencijom ponište? To vrijedi i za svjetlosne snopove.
Neka je put jednog snopa do točke T jednak \(x_{1}\) a drugog \(x_{2}\). Razlika u prijeđenim putevima je
\[\Delta x=x_{2}-x_{1}\]
Snopovi svjetlosti u točki T će se poništiti (destruktivna interferencija) ako je razlika putova koje snopovi prijeđu
\[\Delta x=\left ( 2\,k+1 \right )\frac{\lambda}{2}\]
Ovdje je \(k\) cijeli broj pa je \(2k + 1\) neparan broj.
Do destruktivne interferencije dolazi kada je razlika putova jednaka neparnom broju polovina valne duljine.
17. zadatak
Svemirski brod prolazi brzinom \(0,8\,c\) uz svemirsku postaju. Astronauti u svemirskome brodu u smjeru svojega gibanja izmjere da duljina postaje iznosi
60 m.
Koliku duljinu postaje u smjeru gibanja broda izmjere promatrači smješteni u postaji? Brzina svjetlosti u vakuumu je \(c\).
- A. 36 m
- B. 48 m
- C. 60 m
- D. 100 m
Prisjetite se kontrakcije duljine.
Kontrakciju duljine možemo prikazati kao \[L=L_{0}\sqrt{1-v^{2}/c^{2}}\] \(L\) je duljina postaje koju mjere astronauti u svemirskom brodu, a \(L_{0}\) duljina koju mjere promatrači u postaji. Za \(L_{0}\) dobivamo \[L_{0}=\frac{L}{\sqrt{1-v^{2}/c^{2}}}=100\, \textrm{m}\]
18. zadatak
Dvije čestice različitih masa imaju jednaku de Broglievu valnu duljinu.
Što je od navedenoga točno za te dvije čestice?
- A. Čestica manje mase ima veću količinu gibanja.
- B. Čestica veće mase ima veću količinu gibanja.
- C. Čestica manje mase ima veću brzinu.
- D. Čestica veće mase ima veću brzinu.
Čemu je jednaka de Broglieva valna duljina čestice koja ima masu \(m\) i giba se brzinom \(v\)? Kojim se izrazom može prikazati?
De Broglieva valna duljina čestice mase \(m\) koja se giba brzinom \(v\) jednaka je
\[\lambda =\frac{h}{mv}\]
Ovdje je h Planckova konstanta. Vidimo da će čestice imati jednaku de Broglievu valnu duljinu ako je umnožak \(m\,v\) jednak za obje čestice,
odnosno ako obje čestice imaju jednaku količinu gibanja.
Čestice mogu imati jednaku količinu gibanja ako se čestica manje mase giba većom brzinom.
19. zadatak
Fotoni energije 9 eV dolaze na metalnu pločicu zbog čega iz nje izlaze elektroni kinetičke energije
6 eV.
Kolika je kinetička energija elektrona koji izlaze iz te metalne pločice ako na nju dolaze fotoni energije 18 eV?
- A. 6 eV
- B. 9 eV
- C. 12 eV
- D. 15 eV
U ovom je zadatku riječ o fotoefektu. Kojom je jednadžbom Einstein objasnio fotoefekt?
Prema Einsteinu, energija fotona \(E_{\textrm{f}}\) koji padaju na metal, dijelom se "troši" na svladavanje izlaznog rada, \(W\) (rad kojega je potrebno izvršiti da elektron napusti metal), a dijelom na kinetičku energiju tih elektrona \(E_{\textrm{k}}\). \[E_{\textrm{f}}=W+E_{\textrm{k}}\] Ako uvrstimo podatke za fotone energije \(9\,\textrm{eV}\), možemo izračunati izlazni rad za taj metal \[W=E_{\textrm{f}}-E_{\textrm{k}}=3\,\textrm{eV}\] Fotoni energije \(18\,\textrm{eV}\) izbacivat će elektrone kojima je kinetička energija jednaka \[E_{\textrm{k}}=E_{\textrm{f}}-W=15\,\textrm{eV}\]
20. zadatak
Koju česticu označava \(\textrm{X}\) u nuklearnoj reakciji \[_{20}^{44}\textrm{Ca} +\, _{1}^{1}\textrm{H}\rightarrow \, _{19}^{41}\textrm{K}+\, \textrm{X}\]
- A. elektron
- B. neutron
- C. jezgru vodika
- D. jezgru helija
Za nuklearne reakcije vrijede zakon očuvanja broja protona (redni broj) i broja nukleona (maseni broj).
Prema zakonu očuvanja broja protona vrijedi: \[20+1=19+\textrm{Z}\] Za redni broj nastale čestice dobivamo \[\textrm{Z}=2\] Prema zakonu očuvanja broja nukleona vrijedi: \[44+1=41+\textrm{A}\] Za redni broj nastale čestice dobivamo \[\textrm{A}=4\] Jezgra s rednim brojem 2 i masenim brojem 4 je jezgra helija. Maseni broj u ovom primjeru nismo ni morali određivati.
21. zadatak
Radioaktivni uzorak sadrži \(10^{6}\) radioaktivnih jezgri.
Koliko će ostati neraspadnutih jezgri nakon tri vremena poluraspada toga uzorka?
- A. \(10^{5}\)
- B. \(1,25\cdot 10^{5}\)
- C. \(3,33\cdot 10^{5}\)
- D. \(8\cdot 10^{5}\)
Primijenite zakon radioaktivnog raspada.
Vrijeme poluraspada \(T\) je vrijeme nakon kojega se raspadne polovina radioaktivnih jezgri. Nakon \(2\,T\) raspast će se još polovina preostalih jezgri, odnosno četvrtina od početnog broja i nakon \(3\,T\) raspast će se polovina od preostalog broja jezgri ili jedna osmina od početnog broja. Prema tome, ukupno se raspalo \(1/2+1/4+1/8=7/8\) početnog broja jezgri pa je preostalo \(N/8=1,25\cdot 10^{5}\) jezgri.
22. zadatak
Grafovi prikazuju iznos akceleracije tijela u ovisnosti o vremenu.
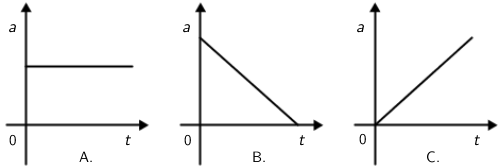
Koji od ponuđenih grafova prikazuje gibanje u kojemu se iznos brzine čitavo vrijeme jednoliko povećava?
- A. graf A
- B. graf B
- C. graf C
Kako nazivamo gibanje kod kojega se brzina tijekom vremena jednoliko povećava? Kako izgleda graf akceleracije za to gibanje?
Radi se o jednoliko ubrzanom gibanju. Graf akceleracije je pravac paralelan s osi \(t\).
23. zadatak
Toplinski stroj radi između dvaju toplinskih spremnika temperatura \(T_{\small{\textrm{A}}}\) i \(T_{\small{\textrm{B}}}\) , tako da vrijedi
\(T_{\small{\textrm{A}}} > T_{\small{\textrm{B}}}\).
Što će se dogoditi s korisnošću toga stroja ako se \(T_{\small{\textrm{B}}}\) smanji, a \(T_{\small{\textrm{A}}}\) ostane nepromijenjena?
- A. Smanjit će se.
- B. Neće se promijeniti.
- C. Povećat će se.
Kako je definirana korisnost toplinskog stroja? Kojim se izrazom može prikazati?
Korisnost toplinskog stroja definirana je kao
\[\eta =\frac{T_{\small{\textrm{A}}}-T_{\small{\textrm{B}}}}{T_{\small{\textrm{A}}}}\]
Vidimo da je ona to veća što je razlika temperatura između toplijeg i hladnijeg spremnika veća.
Ako temperaturu hladnijeg spremnika smanjimo, ta će razlika biti veća, pa će i korisnost biti veća.
Napomena Navedeni izraz za korisnost vrijedi samo za Carnotov stroj.
24. zadatak
Ravni se magnet razdijeli na dva jednaka komada.
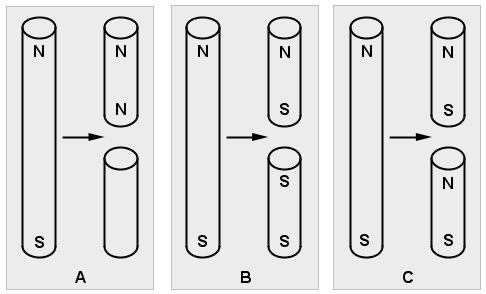
Koji od ponuđenih crteža točno prikazuje dijeljenje magneta?
- A. Crtež A.
- B. Crtež B.
- C. Crtež C.
Može li se dijeljenjem jednog magneta dobiti magnet koji ima dva jednaka pola?
Dijeljenjem magneta na dva dijela uvijek dobijemo dva magneta od kojih svaki ima sjeverni i južni pol.
25. zadatak
Graf prikazuje iznos sile koja djeluje na neko tijelo u ovisnosti o vremenu.
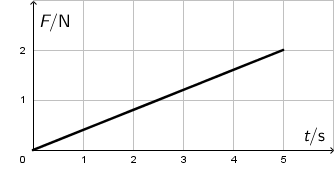
Koliki je impuls sile primilo tijelo tijekom prvih pet sekunda?
Odgovor:
Impuls stalne sile definiramo kao umnožak sile i intervala vremena u kojemu je sila djelovala. Kako ga možemo izračunati ako sila nije stalna?
Ukoliko se sila tijekom vremena mijenja linearno onda možemo uzeti srednju silu i pomnožiti ju s intervalom vremena tijekom kojega je djelovala: \[\bar{F}\cdot \Delta t=\frac{F}{2}\cdot \Delta t=1\cdot 5=5\,\textrm{N}\,\textrm{s}\] Zadatak možemo riješiti i tako da odredimo površinu ispod grafa sile: \[p=\frac{2\cdot 5}{2}=5\,\textrm{Ns}\]
26. zadatak
Tijelo se giba po pravcu. Početna brzina tijela iznosi 5 m/s. Nakon prijeđena 4 m brzina tijela
iznosi 1 m/s.
Koliko iznosi srednja akceleracije tijela? Orijentacija brzine tijela se ne mijenja.
Odgovor: \(\textrm{m}/\textrm{s}^{2}\)
O kakvom se ovdje gibanju radi? Primijenite odgovarajuću izraze koji povezuju akceleraciju i brzinu.
Brzina tijela ne mijenja orijentaciju i smanjuje se pa je gibanje jednoliko usporeno. Iz izraza \[v^{2}=v{_{0}}^{2}-2as\] odredimo akceleraciju. (Kod jednoliko usporenog gibanja trenutna i srednja akceleracija su jednake.) \[a=\frac{v{_{0}}^{2}-v^{2}}{2s}=3\, \frac{\textrm{m}}{\textrm{s}^{2}}\] Napomena: To je iznos akceleracije. Kod jednoliko usporenog gibanja akceleracija je po orijentaciji suprotna orijentaciji brzine. Ako je brzina pozitivna, akceleracija je negativna.
27. zadatak
Srednja kinetička energija nasumičnoga gibanja čestica jednoatomnoga idealnog plina iznosi \(6\cdot 10^{\mathbf{-}20}\,\textrm{J}\).
Kolika je termodinamička temperatura toga plina? Rezultat zaokružite na jednu decimalu
Odgovor:
Čemu je jednaka srednja kinetička energija molekula jednoatomnog idealnog plina? Napšite izraz i izračunajte apsolutnu (ili termodinamičku) temperaturu.
Srednja kinetička energija nasumičnoga gibanja čestica jednoatomnoga idealnog plina jednaka je \[\overline{E}_{k}=\frac{3}{2}kT\] Vrijednost Boltzmannove konstante pronađite u knjižici formula, dok je \(T\) termodinamička temperatura plina. Za termodinamičku temperaturu dobijemo \[T=\frac{2\overline{E}_{\textrm{k}}}{3k}=2898,6\, \textrm{K}\]
28. zadatak
Dva točkasta naboja, \(Q_{1}\) i \(Q_{2}\) međusobno su udaljena 0,1 m. Sila međudjelovanja između naboja iznosi \(F\).
Na kolikoj se međusobnoj udaljenosti trebaju nalaziti naboji \(Q_{1}\) i \(2Q\) da bi sila međudjelovanja između njih također iznosila \(F\)?
Odgovor:
Kojim se izrazom može prikazati električna sila između dva točkasta naboja? Primijenite to na oba slučaja i izračunajte novu udaljenost.
Električna sila između naboja \(Q_{1}\) i \(Q_{2}\) iznosi \[F=k\frac{Q_{1}\cdot Q_{2}}{r^{2}}\] Prema zadatku, jednaka sila djeluje i između naboja \(Q_{1}\) i \(2\,Q\). Traženu udaljenost označimo s \(r_{1}\). \[F=k\frac{Q_{1}\cdot 2Q}{r_{1}^{2}}\] Ako izjednačimo desne strane i skratimo \(k\), \(Q_{1}\) i \(Q_{2}\), dobijemo jednadžbu \frac{1}{r^{2}}=\frac{2}{r_{1}^{2}} Tražena udaljenost je \[r_{1}=\sqrt{2}\cdot r=0,141\, \textrm{m}\]
29. zadatak
Kolika je konstanta optičke rešetke ako se spektar petoga reda svjetlosti valne duljine 500 nm vidi pod kutom od
\(30^{\textrm{o}}\)?
Odgovor:
Ako na optičku rešetku pada svjetlost, dolazi do difrakcije. Iz kojeg izraza možemo odrediti konstantu optičke rešetke?
Konstanta optičke rešetke \(d\), kut pod kojim vidimo neki spektar \(\alpha\), redni broj spektra \(k\) i valna duljina upadne svjetlosti \(\lambda\) povezani su izrazom \[d\cdot \textrm{sin}\, \alpha =k\lambda\] Za konstantu optičke rešetke dobovamo \[d=\frac{k\lambda }{\textrm{sin}\,\alpha}=\frac{5\cdot 5\cdot 10^{\mathbf{-}7}}{0,5}=5\cdot 10^{\mathbf{-}6}\, \textrm{m}\]
30. zadatak
Atom vodika prelazi iz prvoga pobuđenog stanja energije \(-5,44\cdot 10^{\mathbf{-}19}\,\textrm{J}\) u osnovno stanje energije
\(-21,76\cdot 10^{\mathbf{-}19}\,\textrm{J}\).
Kolika je frekvencija elektromagnetskoga zračenja koje je pritom emitirano?
Odgovor:
Prema Bohru, do zračenja elektromagnetskih valova dolazi kada atom prelazi iz višeg energetskog nivoa u niži. Čemu je jednaka energija fotona koji se pri tom emitira? Kako energija fotona ovisi o frekvenciji?
Energija fotona elektromagnetskog zračenja jednaka je
\[E_{\textrm{f}}=h\cdot \nu\]
Vrijednost Planckove konstante \(h\) potražite u knjižici formula.
Ovaj foton nastaje kada atom prelazi iz prvog pobuđenog stanja u osnovno pa vrijedi
\[E_{\textrm{f}}=E_{2}-E_{1}\]
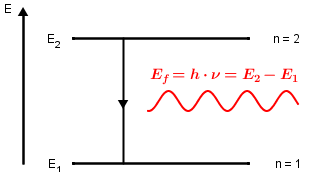
Izjednačimo desne strane ovih jednadžbi i izračunajmo frekvenciju \[\nu =\frac{E_{2}-E_{1}}{h}=2,5\cdot 10^{15}\,\textrm{Hz}\]
31. zadatak
Automobil mase 1000 kg nailazi na ispupčen most polumjera zakrivljenosti 20 m.
Brzina automobila na vrhu mosta iznosi 10 m/s.
Koliki je iznos sile kojom automobil djeluje na most kada se nalazi na vrhu mosta?
Odgovor:
Koje sve sile u vertikalnom smjeru djeluju na automobil u najvišoj točki? Kolika je ukupna sila? Koja je njezina orijentacija?
Na automobil djeluje sila teža \(F_{g}\) vertikalno prema dolje i reakcija podloge \(N\) vertikalno prema gore. Sila teža po iznosu je veća od reakcije podloge jer ukupna sila mora imati smjer prema središtu zakrivljenosti mosta \[F_{g} > N\]
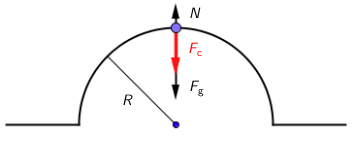
Ukupna sila \(F_{g}-N\) ima ulogu centripetalne sile. \[F_{g}-N=m\cdot \frac{v^{2}}{R}\] Za reakciju podloge dobivamo \[N=F_{g}-m\cdot \frac{v^{2}}{R}\] Nakon što jednadžbu pojednostavimo, dobivamo \[N=m\left ( g-\frac{v^{2}}{R} \right )\] Uvrstimo podatke i izračunajmo \[N=5000\,\textrm{N}\] Napomena: Izračunali smo silu kojom most djeluje na automobil. Prema 3. Newtonovom zakonu tolikom silom i automobil djeluje na most.
32. zadatak
U cilindru s pomičnim klipom nalazi se plin pod tlakom \(2\cdot 10^{5}\,\textrm{Pa}\) pri temperaturi 300 K.
Plin se izobarno stlači na volumen \(0,9\cdot 10^{\mathbf{-}3}\,\textrm{m}^{3}\) i pritom se na plinu obavi rad od 20 J.
Kolika je temperatura plina nakon tlačenja?
Odgovor: K
Kojom se jednadžbom opisuje izobarno tlačenje plina? Koliki rad pri tome okolina okolina? Iz te dvije jednadžbe možete odrediti konačnu temperaturu plina.
Izobarna promjena stanja plina opisuje se jednadžbom
\[\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}\]
Rad plina je negativan: \(W=\mathbf{-}20\,\textrm{J}\).
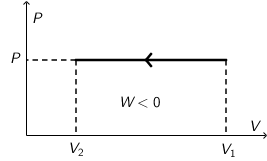 \[W=P\left ( V_{2}-V_{1} \right )\]
Početni volumen jednak je:
\[V_{1}=V_{2}-\frac{W}{P}=10^{\mathbf{-}3}\, \textrm{m}^{3}\]
Odredimo temperaturu plina nakon tlačenja iz prve jednadžbe
\[T_{2}=\frac{V_{2}\,T_{1}}{V_{1}}=270\, \textrm{K}\]
\[W=P\left ( V_{2}-V_{1} \right )\]
Početni volumen jednak je:
\[V_{1}=V_{2}-\frac{W}{P}=10^{\mathbf{-}3}\, \textrm{m}^{3}\]
Odredimo temperaturu plina nakon tlačenja iz prve jednadžbe
\[T_{2}=\frac{V_{2}\,T_{1}}{V_{1}}=270\, \textrm{K}\]
33. zadatak
Bakrena žica duljine 1000 m ima otpor \(1\,\Omega\).
Kolika je masa te žice? Otpornost bakra je \(1,7\cdot 10^{\mathbf{-}8}\,\Omega\,\textrm{m}\), a gustoća \(8900\,\textrm{kg}\,\textrm{m}^{\mathbf{-}3}\).
Rezultat zaokružite na cijeli broj.
Odgovor:
Masu odredimo pomoću gustoće i volumena žice, volumen žice preko duljine i površine poprečnog presjeka, a površinu presjeka pomoću zakona električnog otpora.
Masu žice odredimo kao \[m=\rho_{m}\,V\] \[V = \ell S\] Iz zakona električnog otpora \[R=\rho \frac{\ell}{S}\] odredimo površinu presjeka žice \[S=\frac{\rho \ell}{R}\] Za masu žice dobivamo \[m=\frac{\rho _{m}\,\rho\, \ell^{2}\,}{R}=151\,\textrm{kg}\]
34. zadatak
Uteg mase 0,2 kg harmonijski titra na opruzi konstante elastičnosti 80 N/m s amplitudom
0,1 m.
Kolika je brzina toga utega kada mu je elongacija 0,05 m?
Odgovor:
Napišite jednadžbe za elongaciju i brzinu kod harmonijskog titranja i pomoću njih riješite zadatak.
Jednadžba za elongaciju tijela koje harmonijski titra: \[y=y_{0}\, \textrm{sin}\, \omega t\] Jednadžba za brzinu tijela koje harmonijski titra: \[v=v_{0}\, \textrm{cos}\, \omega t=\omega \, y_{0}\, \textrm{cos}\, \omega t\] Iz prve jednadžbe dobijemo \[\textrm{sin}\, \omega t=\frac{y}{y_{0}}=\frac{0,05}{0,1}=0,5\] Odredimo \(\omega\,t\) \[\omega t=\frac{\pi }{6}\] Pomoću konstante elastičnosti odredimo \(\omega\) \[k=m\omega ^{2}\Rightarrow \omega =\sqrt{\frac{k}{m}}\] Sada možemo odrediti traženu brzinu \[v=\omega\, y_{0}\, \textrm{cos}\, \omega t=\sqrt{\frac{k}{m}}\,y_{0}\, \textrm{cos}\, \omega t\] \[v=\sqrt{\frac{80}{0,2}}\cdot 0,1\cdot \textrm{cos}\, \frac{\pi }{6}=\sqrt{3}=1,73 \, \frac{\textrm{m}}{\textrm{s}}\]
35. zadatak
Tijekom 5 s kružna ploča grijalice promjera 0,1 m u okolinu izrači
500 J energije.
Kolika je temperatura te ploče? Temperatura ploče se za vrijeme zračenja ne mijenja. Zanemarite debljinu ploče.
Rezultat zaokružite na cijeli broj.
Odgovor:
Pretpostavimo da ploča zrači kao apsolutno crno tijelo i primijenimo Stefan-Boltzmannov zakon zračenja crnoga tijela.
Snaga zračenja jednaka je energiji koju ploča zrači u jednoj sekundi. \[P=\frac{E}{t}\] Prema Stefan-Boltzmannovom zakonu snaga zračenja je \[P=\sigma\,S\,T^{4}\] Površina kružne ploče je \[S=r^{2}\pi\] pri čemu je polumjer kružne ploče jednak \(0,05\, \textrm{m}\). Koristeći prethodno napisane izraze, za temperaturu kružne ploče dobivamo \[T=\sqrt[4]{\frac{E}{\sigma r^{2}\pi t}}=688\,\textrm{K}\]