Probni ispit za maturu 2023. godine
1. zadatak
U trenutku uključivanja zelenoga svjetla na semaforu s križanja iz mirovanja počinje ubrzavati automobil akceleracijom
2 m/s2. U susjednome prometnom traku u istome smjeru jednoliko se
pravocrtno giba kamion brzinom 20 m/s.
Kamion se nije zaustavio na križanju i u trenutku polaska automobila prolazi pored njega.
Nakon koliko će vremena automobil sustići kamion?
- A. nakon 5 s
- B. nakon 10 s
- C. nakon 15 s
- D. nakon 20 s
Automobil kreće iz mirovanja i giba se jednoliko ubrzano. Put kojega prijeđe jednak je: \[s_{\small{1}}=\frac{a}{2}t^{2}\] Kamion se giba jednoliko. Put kojega prijeđe kamion jednak je: \[s_{\small{2}}=vt\]
Kada automobil dostigne kamion, oba vozila prevalila su jednak put: \[s_{\small{1}}=s_{\small{2}}\] \[\frac{a}{2}t^{2}=vt\] Iz ovog izraza dobijemo vrijeme nakon kojega je automobil dostigao kamion: \[t=\frac{2\,v}{a}=20\,s\]
2. zadatak
Na tijelo mase m koje klizi niz kosinu djeluje stalna sila F kao što je prikazano na slici. Tijelo se giba niz kosinu akceleracijom a. Sila trenja je zanemariva.
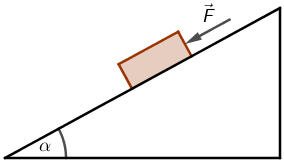
Koliki je iznos sile F?
- A. F = m (a - g cos α)
- B. F = m (a + g cos α)
- C. F = m (a - g sin α)
- D. F = m (a + g sin α)
Nacrtajte dijagram sila koje djeluju na tijelo, odredite rezultantnu silu i primijenite osnovni zakon gibanja.
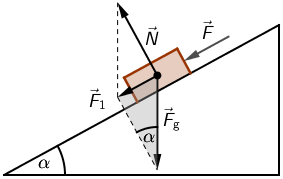
Na tijelo djeluju sile:
- \(\vec{F}\) - sila koja gura tijelo niz kosinu
- \(\vec{F}_{\textrm{g}}=m\,g\) - sila teža
- \(\vec{N}\) - reakcija podloge
Iz crteža vidimo da je sila \(\vec{F}_{1}\) jednaka: \[\vec{F}_{\textrm{1}}=\vec{F}_{\textrm{g}}+\vec{N}\] Njezin iznos odredimo na osnovu osjenčanog trokuta na crtežu: \[F_{\textrm{1}}=m\,g\,\textrm{sin}\,\alpha\] Iznos rezultantne sile na tijelo je \(F_1+F\). Primijenimo drugi Newtonov zakon: \[F_1+F=m\,a\] Sila \(F\) jednaka je: \[F=m\,a-F_1\] \[F=m\,a-m\,g\,\textrm{sin}\,\alpha\] \[F=m\left(a-g\,\textrm{sin}\,\alpha \right)\]
3. zadatak
Dvije osobe vrte se na vrtuljku tako da je jedna bliže, a druga dalje od osi rotacije.
Koja od navedenih fizičkih veličina nije jednaka za obje osobe?
- A. period kruženja
- B. frekvencija
- C. kutna brzina
- D. obodna brzina
-
\(T\) - period kruženja
Vrijeme potrebno da tijelo jednom obiđe kružnicu - \(f\) - frekvencija \[f=\frac{1}{T}\]
-
\(\omega\) - kutna brzina
\[\omega=\frac{2\,\pi}{T}\] -
\(v\) - obodna brzina -
\[v=\frac{2\,r\,\pi}{T}\]
Jedino obodna brzina: \[v=\frac{2\,r\,\pi}{T}\] ovisi o polumjeru kruženja, odnosno o udaljenosti od osi rotacije.
4. zadatak
Masa planeta Marsa iznosi 0,107 mase Zemlje, a polumjer Marsa 0,533 polumjera Zemlje.
Koliko je puta sila teža na neko tijelo na Zemlji veća od sile teže na to tijelo na Marsu?
- A. 1,00
- B. 1,64
- C. 2,65.
- D. 4,98
Sila teža kojom planeta mase \(M\) djeluje na tijelo mase \(m\) na površini planeta polumjera \(R\): \[F=G\,\frac {M\,m}{R^{2}}\]
Sila teža na površini Zemlje: \[F_{\small{\textrm{Z}}}=G\,\frac {M_{\small{\textrm{Z}}}\,m}{R_{\small{\textrm{Z}}}^{2}}\] Sila teža na površini Marsa: \[F_{\small{\textrm{M}}}=G\,\frac {M_{\small{\textrm{M}}}\,m}{R_{\small{\textrm{M}}}^{2}}\] Podijelimo prvu jednadžbu drugom: \[\frac{F_{\small{\textrm{Z}}}}{F_{\small{\textrm{M}}}}=G\,\frac {M_{\small{\textrm{Z}}}\,m}{R_{\small{\textrm{Z}}}^{2}}\cdot \frac{R_{\small{\textrm{M}}}^{2}}{G\,M_{\small{\textrm{M}}}\,m}\] \[\frac{F_{\small{\textrm{Z}}}}{F_{\small{\textrm{M}}}}=\frac {M_{\small{\textrm{Z}}}}{M_{\small{\textrm{M}}}}\cdot \frac{R_{\small{\textrm{M}}}^{2}}{R_{\small{\textrm{Z}}}^{2}}\] \[\frac{F_{\small{\textrm{Z}}}}{F_{\small{\textrm{M}}}}=\frac {M_{\small{\textrm{Z}}}}{M_{\small{\textrm{M}}}}\cdot \left(\frac{R_{\small{\textrm{M}}}}{R_{\small{\textrm{Z}}}}\right)^{2}\] \[\frac{F_{\small{\textrm{Z}}}}{F_{\small{\textrm{M}}}}=\frac {M_{\small{\textrm{Z}}}}{0,107\cdot M_{\small{\textrm{Z}}}}\cdot \left(\frac{0,533\cdot R_{\small{\textrm{Z}}}}{R_{\small{\textrm{Z}}}}\right)^{2}\] \[\frac{F_{\small{\textrm{Z}}}}{F_{\small{\textrm{M}}}}=\frac{1}{0,107}\cdot 0,533^{2}=2,65\]
5. zadatak
Kada se zimi između dalekovoda ovjesi strujni kabel, najmanja udaljenost od najniže točke kabla do tla iznosi
h = 5 m.
Koji od ponuđenih odgovora predstavlja udaljenost h‘
ljeti kada su temperature zraka više?
- A. h‘ < 0 m
- B. 0 m < h‘ < 5 m
- C. h‘ = 5 m
- D. h‘ > 5 m
Duljina žice pri temperaturi \(t\): \[\ell=\ell_{0}\left [ 1+\alpha\,\left(t-t_{0}\right) \right ]\]
-
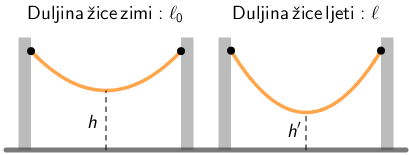
\(\ell_{\,0}\) - duljina žice pri početnoj temperaturi \(t_{0}\)
(Duljina žice zimi) -
\(\ell\) - duljina žice pri konačnoj temperaturi \(t\)
(Duljina žice ljeti) - \(\alpha\)- koeficijent linearnog toplinskog širenja
6. zadatak
Pri kojemu će se od navedenih procesa povećati srednja kinetička energija molekula idealnoga plina?
- A. pri izohornomu smanjenju tlaka
- B. pri izobarnomu povećanju volumena
- C. pri izotermnomu smanjenju volumena
- D. pri izotermnomu povećanju volumena
Srednja kinetička energija molekula idealnog plina proporcionalna je temperaturi plina: \[\bar{E_{\textrm{k}}}\sim k\,T\] Pri kojoj se od navedenih promjena stanja plina mijenja njegova temperatura?
Izohorni proces: \[\frac{p}{T}=\textrm{konst.}\] Izobarni proces: \[\frac{V}{T}=\textrm{konst.}\] Izotermni proces: \[p\,V=\textrm{konst.}\]
Pri izobarnom povećanju volumena: \[\frac{V}{T}=\textrm{konst.}\] povećanjem volumena plina, povećava se i njegova temperatura pa prema tome i srednja kinetička energija molekula idealnog plina.
7. zadatak
Koja je od navedenih tvrdnja točna za toplinu pri dodiru dvaju tijela?
- A. Može prelaziti s tijela manje unutarnje energije na tijelo veće unutarnje energije.
- B. Može spontano prelaziti s tijela niže temperature na tijelo više temperature.
- C. Uvijek prelazi s tijela veće mase na tijelo manje mase.
- D. Uvijek prelazi s tijela veće unutarnje energije na tijelo manje unutarnje energije.
Ako se dva tijela različitih temperatura nalaze u dodiru, unutarnja energija prelazit će sa tijela više temperature na tijelo niže
temperature sve dok se temperature oba tijela ne izjednače. To stanje nazivamo toplinska ravnoteža.
Dio unutarnje energije koji je prešao s tijelo više na tijelo niže temperature nazivamo toplinom \(Q\):
\[Q=\Delta U\]
-
Prema drugom zakonu termodinamike, toplina spontano može prelaziti samo s tijela više na tijelo niže temperature.
Tvrdnja B nije točna. -
Ako tijelo manje mase ima višu temperaturu, toplina će prelaziti na tijelo veće mase.
Tvrdnja C nije točna. -
Ako u more stavimo bočicu toplog čaja, čaj će se ohladiti jer će toplina prelaziti u more iako je unutarnja energija mora
puno veća od unutarnje energije čaja.
Tvrdnja D nije točna. - Posljednji primjer pokazuje nam da je točna tvrdnja A.
8. zadatak
Idealni toplinski stroj prima toplinu od toplijega spremnika temperature
U kojemu će se od navedenih slučajeva povećati korisnost toplinskoga stroja?
- A. kada se temperature obaju spremnika povećaju za isti iznos ΔT
- B. kada se temperature obaju spremnika smanje za isti iznos ΔT
- C. kada temperatura toplijega spremnika ostane ista i kada se temperatura hladnijega spremnika poveća za ΔT
- D. kada temperatura hladnijega spremnika ostane ista i kada se temperatura toplijega spremnika smanji za ΔT
Korisnost idealnog toplinskog stroja \(\eta\) \[\eta=\frac{T_{1}-T_{2}}{T_{1}}\]
- \(T_{1}\) - temperatura toplijeg spremnika
- \(T_{2}\) - temperatura hladnijeg spremnika
Ako smanjimo temperature toplijeg i hladnijeg spremnika za \(\Delta T\), korisnost idealnog toplinskog stroja bit će:
\[\eta=\frac{T_{1}-T_{2}}{T_{1}}\]
\[\eta=\frac{T_{1}-\Delta T-\left(T_{2}-\Delta T\right)}{T_{1}-\Delta T}\]
\[\eta=\frac{T_{1}-T_{2}}{T_{1}-\Delta T}\]
Brojnik razlomka ostao je isti, a nazivnik se smanjio. To znači da se razlomak povećao.
Točan odgovor je B.
9. zadatak
Na slici je prikazano električno polje naboja q1 i q2.
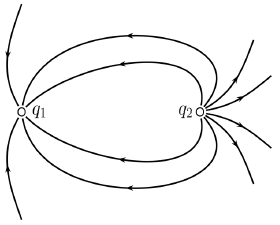
Koja od navedenih tvrdnja ispravno opisuje prikaz na slici?
- A. │q1│ < │q2│ i q2 < 0
- B. │q1│ < │q2│ i q2 > 0
- C. │q1│ > │q2│ i q2 > 0
- D. │q1│ > │q2│ i q2 < 0
Električne silnice
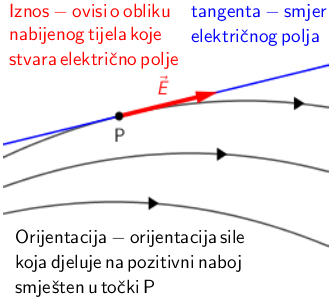
Silnice električnog polja (linije sile) omogućuju zoran prikaz električnog polja. Kroz svaku točku u električnom polju prolazi jedna električna silnica. Električna silnica je zamišljena linija (crta) koja slijedi smjer električnog polja. Električni naboj, stavljen u neku točku električnog polja i pušten da se polagano giba, išao bi uzduž silnice koja prolazi tom točkom.
-
Silnice izlaze iz pozitivnog naboja, a ulaze u negativni naboj.
-
Iznos električnog polja veći je na onom mjestu na kojemu je veća gustoća silnica, odnosno tamo gdje su silnice bliže jedna drugoj.
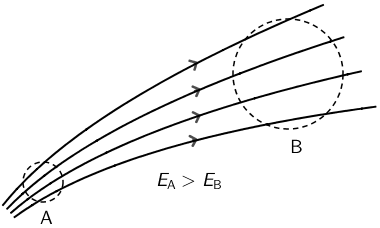
Iznos električnog polja u području A veći je nego u području B jer su silnice u području A gušće nego u području B. -
Broj silnica koje izlaze iz pozitivnog ili ulaze negativni naboj proporcionalan je iznosu naboja.
Naboj \(q_{1}\) veći je od naboja \(q_{2}\) jer iz njega izlazi više silnica nego što ih ulazi u naboj \(q_{2}\).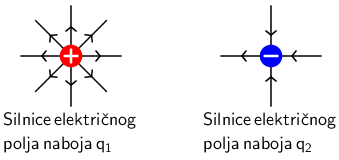
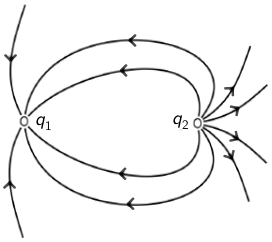
Silnice izviru iz naboja \(q_{2}\), a poniru u naboj \(q_{1}\). Prema tome, naboj \(q_{2}\) je pozitivan, a naboj \(q_{1}\) negativan.
Iz naboja \(q_{2}\) izvire više silnica nego iz naboja \(q_{1}\) pa je iznos naboja \(q_{2}\) veći od iznosa naboja \(q_{1}\).
│q1│ < │q2│ i q2 > 0
10. zadatak
Pločasti kondenzator priključen je na izvor stalnoga napona. Iznos naboja na pojedinoj ploči jednak je
q0 , a iznos električnoga polja između ploča kondenzatora jednak je
E0. Poveća se razmak ploča kondenzatora, dok kondenzator ostaje
spojen na isti izvor napona.
Kako će se zbog toga promijeniti električno polje i iznos naboja na pojedinoj ploči kondenzatora?
- A. E > E0 , q > q0
- B. E > E0 , q < q0
- C. E < E0 , q > q0
- D. E < E0 , q < q0
Kapacitet pločastog kondenzatora: \[C=\varepsilon_{0}\,\varepsilon_{r}\,\frac {S}{d}\]
- \(\varepsilon_{0}\) - permitivnost vakuuma
- \(\varepsilon_{\textrm{r}}\) - relativna permitivnost (permitivnost sredstva koje je umetnuto između ploča)
- \(S\) - površina ploče
- \(d\) - udaljenost između ploča
Električno polje između ploča kondenzatora: \[E=\frac{U}{d}\]
- \(U\) - napon između ploča
\[C=\varepsilon_{0}\,\varepsilon_{r}\,\frac {S}{d}\]
Povećanjem razmaka između ploča kapacitet kondenzatora se smanjuje.
Naboj na pločama kondenzatora:
\[q=C\,U\]
također se smanjuje jer je napon između ploča ostao isti.
\[E=\frac{U}{d}\] Povećanjem razmaka između ploča električno polje između ploča također se smanjuje jer je napon između ploča ostao isti.
11. zadatak
Na slici je prikazana shema spoja triju otpornika.
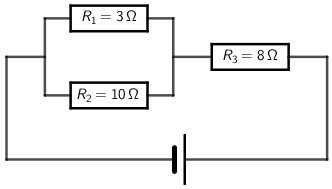
Koja je od navedenih tvrdnja za prikazani spoj otpornika točna?
- A. Najveći je napon na krajevima otpornika R3.
- B. Najveća struja prolazi otpornikom R1.
- C. Najveći je napon na krajevima otpornika R2.
- D. Najmanja struja prolazi otpornikom R1.
Prisjetite se paralelnog i serijskog spajanja otpora: Spajanje otpora i Kirchhoffova pravila
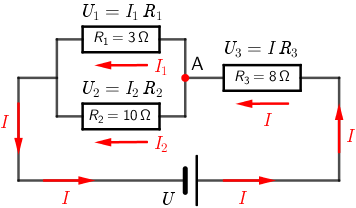
B. Najveća struja prolazi otpornikom \(R_{1}\).
U točki grananja A vrijedi prvo Kirchhoffovo pravilo:
\[I=I_{1}+I_{2}\]
Iz navedenog izraza zaključujemo da je \(I_{1} < I\) i \(I_{2} < I\).
Prema tome, tvrdnja B nije točna.
C. Najveći je napon na krajevima otpornika \(R_{2}\).
Napon na krajevima otpornika \(R_{2}\) jednak je naponu na krajevima otpornika \(R_{1}\) jer su ti otpornici
spojeni paralelno.
Tvrdnja C nije točna
D. Najmanja struja prolazi otpornikom \(R_{1}\).
\[U_{1}=U_{2}\] \[I_{1}\,R_{1}=I_{2}\,R_{2}\] \[I_{1}=\frac{R_{2}}{R_{1}}\cdot I_{2}\] \[I_{1}=\frac{10}{3}\cdot I_{2}\Rightarrow I_{1} > I_{2}\] Tvrdnja D nije točna.
Pokažimo da je točna tvrdnja A. Nacrtajmo ekvivalentnu shemu:
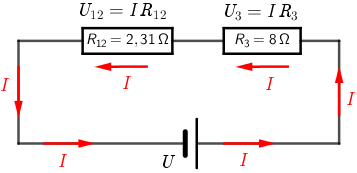
Ekvivalentni otpor paralelno spojenih otpornika \(R_{1}\) i \(R_{2}\) jednak je: \[R_{12}=\frac{R_{1}\,R_{2}}{R_{1}+R_{2}}=2,31\,\Omega\] Kroz otpornike \(R_{12}\) i \(R_{3}\) prolazi ista struja: \[\frac{U_{3}}{U_{12}}=\frac{I\,R_{3}}{I\,R_{12}}=\frac{8}{2,31}=3,47\] Prema tome, \(U_{3} > U_{12}\)
12. zadatak
Ravnim metalnim vodičem otpornosti ρ, poprečnoga presjeka S i duljine ℓ koji se giba
okomito na silnice homogenoga magnetskog polja brzinom v prolazi inducirana struja
I.
Koji je od navedenih izraza za induciranu struju točan?
- A. \(I=\Large{\frac{B\,S\,v}{\rho}}\)
- B. \(I=\Large{\frac{B\,\ell^{\,2}\,v}{\rho}}\)
- C. \(I=\Large{\frac{B\,S\,v}{\rho\,\ell^{\,2}}}\)
- D. \(I=\Large{\frac{B\,\rho\,S\,v}{\ell^{\,2}}}\)
Faradayev zakon
Inducirani elektromotorni napon u ravnom vodiču koji se giba u magnetskom polju:
\[U_{\textrm{i}}=B\,\ell\,v\,\textrm{sin}\,\alpha\]
Ako se vodič giba okomito na magnetsko polje kut \(\alpha=90^{o}\) pa je inducirani napon jednak:
\[U_{\textrm{i}}=B\,\ell\,v\]
Induciranu struju odredimo pomoću Ohmovog zakona, a otpor vodiča pomoću zakona električnog otpora.
Otpor vodiča: \[R=\rho\cdot \frac{\ell}{S}\] Ohmov zakon: \[I_{\textrm{i}}=\frac{U_{\textrm{i}}}{R}\] \[I_{\textrm{i}}=\frac{B\,\ell\,v}{\rho\cdot \large{\frac{\ell}{S}}}\] \[I_{\textrm{i}}=\frac{B\,S\,v}{\rho}\]
13. zadatak
Harmonički oscilator sastoji se od tijela mase m koje titra na opruzi konstante elastičnosti
k amplitudom A.
Koliki je iznos rada koji obavi vanjska sila ako amplituda titranja nakon njezina djelovanja iznosi
2 A?
- A. \(\frac{1}{2}\,k\,A^{2}\)
- B. \(k\,A^{2}\)
- C. \(\frac{3}{2}\,k\,A^{2}\)
- D. \(2\,k\,A^{2}\)
Elastična potencijalna energija harmonijskog titranja: \[E_{\textrm{pe}}=\frac{1}{2}k\,A^{2}\]
Rad kojega obavi vanjska sila jednak je promjeni elastične potencijalne energije.
Elastična potencijalna energija prije djelovanja vanjske sile: \[E_{\textrm{pe1}}=\frac{1}{2}k\,A^{2}\] Elastična potencijalna energija nakon djelovanja vanjske sile: \[E_{\textrm{pe2}}=\frac{1}{2}k\,\left(2A\right)^{2}=\frac{4}{2}k\,A^{2}\] Rad je jednak promjeni elastične potencijalne energije: \[W=E_{\textrm{pe2}}-E_{\textrm{pe1}}\] \[W=\frac{3}{2}\,k\,A^{2}\]
14. zadatak
Zadana je jednadžba vala \[y=2\,\textrm{cm sin}\left(\pi\,\textrm{s}^{-1}\,t-2\,\pi\,\textrm{m}^{-1}\,x\right).\] Koliki je najveći iznos brzine titranja neke čestice sredstva kojim se val širi?
- A. 0,0628 m/s
- B. 0,1256 m/s
- C. 0,2512 m/s
- D. 6,28 m/s
Jednadžba harmonijskog vala: \[y\left ( x,\,t \right )=A\,\textrm{sin}\left (\omega \,t - k\,x\right)\]
- \(A\) - amplituda vala
- \(\omega=\Large{\frac{2\,\pi}{T}}\) - kružna frekvencija
- \(k=\Large{\frac{2\,\pi}{\lambda}}\) - valni broj
Najveća brzina titranja čestica sredstva pri širenju harmonijskog vala: \[v_{0}=\frac{2\,A\,\pi}{T}\]
Uspoređivanjem valne jednadžbe i jednadžbe iz zadatka \[y\left ( x,\,t \right )=A\,\textrm{sin}\left (\omega \,t - k\,x\right)\] \[y\left ( x,\,t \right )=2\,\textrm{sin}\left (\pi \,t - 2\,\pi\,x\right)\] zaključujemo: \[A=2\,\textrm{cm}=0,02\,\textrm{m}\] \[\omega=\pi\,\textrm{s}^{-1}\] Odredimo period: \[T=\frac{2\,\pi}{\omega}=2\,\textrm{s}\] Najveći iznos brzine kojom titraju čestice sredstva: \[v_{0}=\frac{2\,A\,\pi}{T}=\frac{2\cdot 0,02\cdot 3,14}{2}\] \[v_{0}=0,0628\,\textrm{m/s}\]
15. zadatak
Kada se izvor zvuka frekvencije 500 Hz približava brzinom v studentu
fizike koji miruje, on čuje zvuk frekvencije f1.
Kada se student brzinom v približava istomu izvoru zvuka koji miruje, čuje zvuk frekvencije
f2.
Koja je od navedenih tvrdnja za odnos frekvencija točna?
- A. f1 = f2 > 500 Hz
- B. f1 = f2 < 500 Hz
- C. f1 > f2 > 500 Hz
- D. f2 > f1 > 500 Hz
Kada nam se približava izvor zvuka čujemo zvučne valove veće frekvencije od one kada izvor miruje.
Kada se izvor udaljava od nas, frekvencija zvučnih valova koju čujemo manja je nego kada izvor miruje. Promjenu frekvencije
zvuka čujemo i ako izvor miruje, a mi se gibamo. Kada se približavamo izvoru, frekvencija zvuka koji dolazi do nas veća je,
a kad se udaljavamo od njega, manja je.
Promjena frekvencije zvuka zbog relativnoga gibanja izvora zvuka u odnosu prema slušatelju naziva se Dopplerov učinak.
Frekvencija zvuka koju prima slušatelj može ze odrediti iz sljedećeg izraza: \[f=f_{\textrm{i}}\,\frac{v_{\textrm{z}} + v_{\textrm{s}}}{v_{\textrm{z}} - v_{\textrm{i}}}\]
Značenje oznaka u ovom izrazu:
- \(f\) - frekvencija zvuka koju prima slušatelj
- \(f_{\textrm{i}}\) - frekvencija zvuka koju emitira izvor
- \(v_{\textrm{z}}\) - brzina zvuka
- \(v_{\textrm{s}}\) - brzina slušatelja
- \(v_{\textrm{i}}\) - brzina izvora zvuka
- \(v_{\textrm{i}} > 0\) - izvor zvuka približava se slušatelju
- \(v_{\textrm{i}} < 0 \) - izvor zvuka udaljava se od slušatelja
- \(v_{\textrm{s}} > 0\) - slušatelj se približava se izvoru zvuka
- \(v_{\textrm{s}} < 0\) - slušatelj se udaljava od izvora zvuka
Prilagodimo izraz \[f=f_{\textrm{i}}\,\frac{v_{\textrm{z}} + v_{\textrm{s}}}{v_{\textrm{z}} - v_{\textrm{i}}}\] oznakama u zadatku:
Izvor zvuka se približava brzinom \(v\) mirnom slušatelju
\[f_{\textrm{i}}=500\,\textrm{Hz}\] \[v_{\textrm{i}}=v\] \[v_{\textrm{s}}=0\] \[f_{1}=500\cdot \frac{v_{\textrm{z}}+ 0}{v_{\textrm{z}} - v}\] \[f_{1}=500\cdot \frac{v_{\textrm{z}}}{v_{\textrm{z}} - v}\qquad(1)\] U izrazu (1) brojnik razlomka veći je od nazivnika pa zaključujemo: \[f_{1}>500\,\textrm{Hz}\]
Slušatelj se približava brzinom \(v\) mirnom izvoru zvuka
\[f_{\textrm{i}}=500\,\textrm{Hz}\] \[v_{\textrm{i}}=0\] \[v_{\textrm{s}}=v\] \[f_{2}=500\cdot \frac{v_{\textrm{z}}+ v}{v_{\textrm{z}} - 0}\] \[f_{2}=500\cdot \frac{v_{\textrm{z}}+v}{v_{\textrm{z}}}\qquad(2)\] U izrazu (2) brojnik razlomka veći je od nazivnika pa zaključujemo: \[f_{2}>500\,\textrm{Hz}\]
Podijelimo izraz (1) izrazom (2): \[\frac{f_{1}}{f_{2}}=500\cdot \frac{v_{\textrm{z}}}{v_{\textrm{z}} - v}:500\cdot \frac{v_{\textrm{z}}+v}{v_{\textrm{z}}}\] \[\frac{f_{1}}{f_{2}}=\frac{v_{\textrm{z}}}{v_{\textrm{z}} - v}\cdot \frac{v_{\textrm{z}}}{v_{\textrm{z}}+v}\] \[\frac{f_{1}}{f_{2}}=\frac{v_{\textrm{z}}^{2}}{v_{\textrm{z}}^{2}-v^{2}}\] Brojnik razlomka veći je od nazivnika pa je razlomak veći od jedan. Zaključujemo da je: \[f_{1} > f_{2}\]
16. zadatak
Svjetlost iz nekoga optičkog sredstva upada na granicu sa zrakom pod kutom
30o.
U kojemu će se od navedenih sredstava indeksa loma n svjetlost totalno reflektirati?
- A. u glicerolu n = 1,47
- B. u jantaru n = 1,55
- C. u staklu n = 1,62
- D. u dijamantu n = 2,42
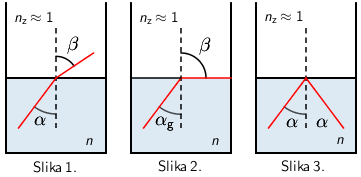
Zraka svjetlosti upada iz optički gušćeg u optički rjeđe sredstvo
- \[n\cdot \textrm{sin}\,\alpha=n_{z}\cdot \textrm{sin}\,\beta\qquad(\textrm{Slika 1.})\]
- \[n\cdot \textrm{sin}\,\alpha_{\textrm{g}}=n_{z}\cdot \textrm{sin}\,\beta\qquad(\textrm{Slika 2.})\] \[\textrm{sin}\,\alpha_{\textrm{g}}\textrm{ - granični kut totalne refleksije.}\] \[\textrm{sin}\,\alpha_{\textrm{g}}=\frac{n_{z}\cdot \textrm{sin}\,\beta}{n}\]
- \[\alpha \gt \alpha_{\textrm{g}}\textrm{ - totalna refleksija.}\qquad (\textrm{Slika 3.})\] \[\textrm{sin}\,\alpha_{\textrm{g}}=\frac{1}{n}\]
Do totalne refleksije dolazi ako je kut upadanja svjetlosti veći od graničnog kuta sredstva iz kojega svjetlost upada na granicu sa zrakom: \[\alpha \gt \alpha_{\textrm{g}}\] Pomoću izraza \[\textrm{sin}\,\alpha_{\textrm{g}}=\frac{1}{n}\] odredimo granični kut za sva četiri sredstva:
- \(\textrm{glicerol: }n=1,47\Rightarrow \alpha_{\textrm{g}}=42,86^{\textrm{o}}\)
- \(\textrm{jantar: }n=1,55\Rightarrow \alpha_{\textrm{g}}=40,18^{\textrm{o}}\)
- \(\textrm{staklo: }n=1,62\Rightarrow \alpha_{\textrm{g}}=38,12^{\textrm{o}}\)
- \(\textrm{dijamant: }n=2,42\Rightarrow \alpha_{\textrm{g}}=16,6^{\textrm{o}}\)
Uvjet za totalnu refleksiju, \(\alpha \gt \alpha_{\textrm{g}}\) ispunjen je jedino za dijamant
17. zadatak
U Youngovu pokusu na zastoru se vide svijetle pruge koje nastaju interferencijom svjetlosti s dvaju točkastih koherentnih
izvora.
Koja je od navedenih tvrdnja točna ako se poveća udaljenost između zastora i izvora?
- A. Poveća se udaljenost između susjednih pruga, a ne promijeni im se boja.
- B. Smanji se udaljenost između susjednih pruga, a ne promijeni im se boja.
- C. Poveća se udaljenost između susjednih pruga i promijeni im se boja.
- D. Smanji se udaljenost između susjednih pruga i promijeni im se boja.
Udaljenost između svjetlih pruga interferencije u Youngovom pokusu jednaka je: \[s=\frac{\lambda\,a}{d}\]
- \(s\) - udaljenost između susjednih svjetlih ili tamnih pruga.
- \(\lambda\) - valna duljina upadne svjetlosti.
- \(d\) - udaljenost između pukotina kroz koje prolazi svjetlost.
- \(a\) - udaljenost između zastora i pukotina kroz koje prolazi svjetlost.
Iz izraza za udaljenost između svjetlih pruga interferencije:
\[s=\frac{\lambda\,a}{d}\]
zaključujemo da će se udaljenost između susjednih svjetlih pruga povećati.
Boja pruga neće se promijeniti jer se ne mijenja ni boja svjetlosti koja upada na pukotine.
18. zadatak
U kojemu od navedenih dijelova spektra elektromagnetskih valova foton ima najveću energiju?
- A. u mikrovalovima
- B. u infracrvenome zračenju
- C. u ultraljubičastome zračenju
- D. u rendgenskome zračenju
Spektar elektromagnetskih valova
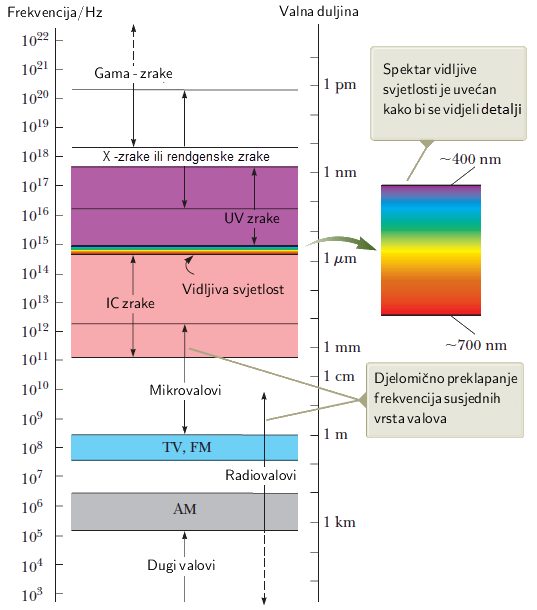
Energija fotona: \[E_{\textrm{f}}=\frac{h\,c}{\lambda}\] Energija je obrnuto proporcionalna valnoj duljini. Iz priložene slike vidimo da od predloženih valova najmanju valnu duljinu imaju rendgenske zrake.
19. zadatak
Frekvencija svjetlosti koja upada na metalnu ploču tri je puta veća od granične frekvencije metala izlaznoga rada
Wi
Kolika je kinetička energija izbačenih fotoelektrona
Ek?
- A. \(E_{\textrm{k}}=\Large{\frac{W_{\textrm{i}}}{3}}\) \(\\\)
- B. \(E_{\textrm{k}}=\Large{\frac{W_{\textrm{i}}}{2}}\)
- C. \(E_{\textrm{k}}=2\,W_{\textrm{i}}\)
- D. \(E_{\textrm{k}}=3\,W_{\textrm{i}}\)
Einsteinova jednadžba fotoefekta: \[E_{\textrm{f}}=W_{\textrm{i}}+E_{\textrm{k}}\] \[E_{\textrm{f}}=h\,f\] Fotoelektrični učinak počinje se opažati kada je energija fotona upravo jednaka izlaznom radu i tada je kinetička energija otoelektrona jednaka nuli. Fotoelektroni su tek napustili metal, ali još nemaju dovoljno energije da se gibaju. Frekvencija pri kojoj je energija fotona jednaka izlaznom radu je granična frekvencija: \[h\,f_{0}=W_{\textrm{i}}\]
U Einsteinovu jednadžbu uvrstimo \(E_{\textrm{k}}=0\) i \(E_{\textrm{f}}=3\,h\,f_{0}\):
\[3\,h\,f_{0}=W_{\textrm{i}}+E_{\textrm{k}}\]
\[E_{\textrm{k}}=3\,h\,f_{0} -h\,f_{0}\]
\[E_{\textrm{k}}=2\,h\,f_{0}\]
\[E_{\textrm{k}}=2\,W_{\textrm{i}}\]
20. zadatak
Zadan je energijski spektar atoma vodika kao što je prikazano na slici.
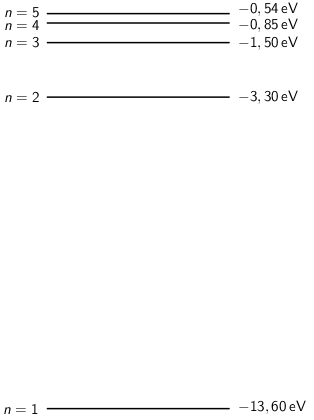
Kod kojega se od navedenih prijelaza u vodikovu atomu emitira foton najveće valne duljine?
- A. n = 1 → n = 2
- B. n = 2 → n = 1
- C. n = 2 → n = 5
- D. n = 5 → n = 2
Atomi ne mogu poprimiti bilo koju energiju, nego samo neke točno određene vrijednosti energije. Te energije zovemo energijske
razine. O vrsti atoma ovise vrijednosti tih dopuštenih energija. Stanje u kojemu se nalazi atom kada mu je energija najmanja
zove se osnovno stanje. Sva druga stanja su pobuđena stanja.
Skup svih dopuštenih energijskih stanja nekog atoma zovemo energijski spektar. Energijski spektar atoma je kvantiziran.
To znači da atom može poprimiti samo točno određene vrijednosti energije.
Ako se atom nađe u nekom pobuđenom stanju, prelazit će spontano u niža energijska stanja sve dok ne dođe do osnovnog stanja.
Pritom atom emitira fotone elektromagnetskog zračenja kojima je energija jednaka razlici energija početnog i konačnog stanja:
\[E_{\textrm{f}}=E_{\textrm{poč}}-E_{\textrm{kon}}\]
Ovaj proces nazivamo emisija zračenja.
Energija fotona kojeg emitira atom pri prijelazu iz višeg u niže energijsko stanje
\[E_{\textrm{f}}=E_{\textrm{poč}}-E_{\textrm{kon}}\qquad(1)\]
može se prikazati kao:
\[E_{\textrm{f}}=h\,f\]
ili kao
\[E_{\textrm{f}}=\frac{h\,c}{\lambda}\]
Valna duljina emitirane svjetlosti obrnuto je proporcionalna energiji fotona:
\[\lambda=\frac{h\,c}{E_{\textrm{f}}}\]
Prema izrazu (1) valnu duljinu emitirane svjetlosti možemo prikazati kao:
\[\lambda=\frac{h\,c}{E_{\textrm{poč}}-E_{\textrm{kon}}}\]
Valna duljina emitiranih fotona bit će najveća ako je razlika energija početnog i končnog stanja najmanja.
Iz energijskog spektra prikazanog na slici vidimo da se radi o prijelazu
\[n=5 \rightarrow n=2 \]
21. zadatak
Koji od navedenih izraza predstavlja moguću nuklearnu reakciju?
- A. 10 B + α → 13 N + p
- B. 10 B + n → 11 B + β-
- C. 23 Na + p → 20 Ne + α
- D. 14 N + p → 13 C + β+
Jezgra atoma nalazi se se u njegovom središtu. Iako je njezin promjer jako malen, u njoj je koncentrirano oko 99,99% mase atoma.
Sastoji se od protona i neutrona, koje nazivamo zajedničkim imenom nukleoni. Broj protona u jezgri,
\(Z\), nazivamo atomskim ili protonskim brojem. Atomski broj jednak
je rednom broju atoma u periodnom sustavu. Ukupan broj nukleona u jezgri, \(A\) , nazivamo
atomskim ili nukleonskim brojem.
Broj neutrona u jezgri jednak je \(N=A-Z\).
Jezgru nekog atoma X simbolički prikazujemo kao: \[_{Z}^{A}\,\textrm{X}\]
U nuklearnim reakcijama vrijede sljedeći zakoni očuvanja:
-
Očuvanje električnog naboja: \(Z_{1}+Z_{2}=Z_{3}+Z_{4}\).
Broj protona prije reakcije \(Z_{1}+Z_{2}\), jednak je broju protona nakon reakcije \(Z_{3}+Z_{4}\). -
Očuvanje broja nukleona: \(A_{1}+A_{2}=A_{3}+A_{4}\).
Broj nukleona prije reakcije \(A_{1}+A_{2}\), jednak je broju nukleona nakon reakcije \(A_{3}+A_{4}\). -
Očuvanje ukupne relativističke energije: \(E_{1}+E_{2}=E_{3}+E_{4}\).
Ukupna energija prije reakcije \(E_{1}+E_{2}\), jednaka je ukupnoj energiji nakon reakcije \(E_{3}+E_{4}\). -
Očuvanje količine gibanja: \(p_{1}+p_{2}=p_{3}+p_{4}\).
Ukupna količina gibanja prije reakcije \(p_{1}+p_{2}\), jednaka je ukupnoj količini gibanja nakon reakcije \(p_{3}+p_{4}\).
Reakcije ponuđene u zadatku nadopunimo uz pomoć periodnog sustava elemenata:
A. \({_{\,\,5}^{10}}\,\textrm{B}+{_{2}^{4}}\,\textrm{He}\rightarrow {_{\,\,7}^{13}}\,\textrm{N}+{_{1}^{1}}\,\textrm{p}\)
Električni naboj nije očuvan: 5 + 2 ≠ 7 + 1
Broj nukleona je očuvan: 10 + 4 = 13 + 1
B. \({_{\,\,5}^{10}}\,\textrm{B}+{_{0}^{1}}\,\textrm{n}\rightarrow {_{\,\,5}^{11}}\,\textrm{B}+{_{-1}^{\,\,\,0}}\,\textrm{e}\)
Električni naboj nije očuvan: 5 + 0 ≠ 5 - 1
Broj nukleona je očuvan: 10 + 1 = 11 + 0
C. \({_{11}^{23}}\,\textrm{Na}+{_{1}^{1}}\,\textrm{p}\rightarrow {_{10}^{20}}\,\textrm{Ne}+{_{2}^{4}}\,\textrm{He}\)
Električni naboj je očuvan: 11 + 1 = 10 + 2
Broj nukleona je očuvan: 23 + 1 = 20 + 4
D. \({_{\,\,7}^{14}}\,\textrm{N}+{_{1}^{1}}\,\textrm{p}\rightarrow {_{\,\,6}^{13}}\,\textrm{C}+{_{+1}^{\,\,\,0}}\,\textrm{e}\)
Električni naboj nije očuvan: 7 + 1 ≠ 6 + 1
Broj nukleona nije očuvan: 14 + 1 ≠ 13 + 0
22. zadatak
Koja je od navedenih tvrdnja za \(\beta^{\mathbf{+}}\) raspad točna?
- A. Maseni broj jezgre smanji se za jedan.
- B. Maseni broj jezgre poveća se za jedan.
- C. Atomski broj jezgre smanji se za jedan.
- D. Atomski broj jezgre poveća se za jedan.
Jednadžba beta-plus raspada: \[{_\textrm{Z}^\textrm{A}}\,\textrm{X}\rightarrow {_{\textrm{Z}\texttt{-}1}^{\,\,\,\,\textrm{A}}}\,\textrm{Y}+{_{\texttt{+}1}^{\,\,0}}\,\textrm{e}+\nu\] Atomski broj je očuvan, a maseni se broj ne mijenja.
- \(Z\) - protonski broj koji je jednak broju protona u jezgri
- \(A\) - nukleonski broj koji je jednak broju nukleona u jezgri. Nukleoni su protoni i neutroni.
- \(\textrm{X,Y}\) - simbolički znak jezgre atoma koji je jednak kemijskom simbolu atoma kojemu jezgra pripada.
- \({_{0}^{0}}\,\nu\) - neutrino
Iz jednadžbe beta-plus raspada \[{_\textrm{Z}^\textrm{A}}\,\textrm{X}\rightarrow {_{\textrm{Z}\texttt{-}1}^{\,\,\,\,\textrm{A}}}\,\textrm{Y}+{_{\texttt{+}1}^{\,\,0}}\,\textrm{e}+\nu\] vidimo da se atomski broj nastale jezgre \({_{\textrm{Z}\texttt{-}1}^{\,\,\,\,\textrm{A}}}\,\textrm{Y}\) smanjio za jedan.
23. zadatak
Mion je nestabilna čestica čiji životni vijek mjeren u vlastitome sustavu iznosi
2·10−6 s.
Koliki je izmjereni životni vijek miona koji se giba brzinom \(v=c\, \large{\sqrt{\frac{99}{100}}}\) u odnosu na mjeritelja?
- A. 2·10−5 s
- B. 2·10−6 s
- C. 2·10−7 s
- D. 2·10−8 s
Relativistička dilatacija vremena: \[\Delta t=\frac{\Delta t_{0}}{\sqrt{1-v^2/c^2}}\]
- \(\Delta t_{0}\) - interval vremena izmjeren u sustavu u odnosu na kojega ura miruje (sustav miona.)
- \(\Delta t\) - interval vremena izmjeren u sustavu u odnosu na kojega se ura giba brzinom v (sustav mjeritelja.)
\[\Delta t_{0}=2\cdot 10^{-6}\,\textrm{s}\] \[\Delta t=\frac{\Delta t_{0}}{\sqrt{1-v^2/c^2}}\] \[\frac{v}{c}=\sqrt{\frac{99}{100}}\] \[\frac{v^{2}}{c^{2}}=\frac{99}{100}\] \[\Delta t=\frac{2\cdot 10^{-6}}{\sqrt{1-\frac{99}{100}}}=\frac{2\cdot 10^{-6}}{\frac{1}{10}}\] \[\Delta t=2\cdot 10^{-5}\,\textrm{s}\]
24. zadatak
Koja od navedenih sila najviše pridonosi držanju protona na okupu u atomskoj jezgri?
- A. slaba nuklearna sila
- B. jaka nuklearna sila
- C. elektromagnetska sila
- D. gravitacijska sila
Protoni su čestice koje su građene od dva u kvarka i jednog d kvarka.
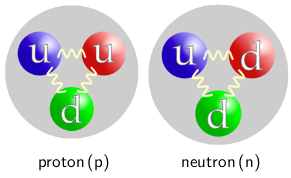
Električni naboji u i d kvarka jednaki su:
\[q_{u}=\frac{2}{3}\,e;\,q_{d}=-\frac{3}{3}\,e\]
Zbog toga je električni naboj protona pozitivan i jednak:
\[q_{p}=\left|e\right|\]
Električni naboj neutrona jednak je nuli:
\[q_{n}=0\]
Osim električnog naboja kvarkovi imaju i "naboj boje", zbog čega međusobno djeluju jakom silom. Jaka sila je privlačna.
Ako je udaljenost između protona u jezgri vrlo mala, jaka sila je oko 100 puta veća od elektromagnetske.
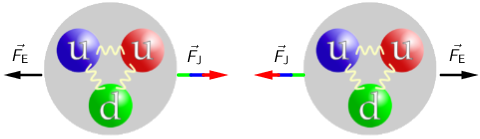
I jaka i elektromagnetska sila smanjuju se ako se udaljenost između protona povećava, međutim, jaka se sila puno brže
smanjuje od elektromagnetske.
Jaka sila djeluje između kvarkova unutar protona i neutrona. Međutim, rezidualna ("preostala") jaka sila
djeluje između kvarkova u jednom protonu i kvarkova u drugom protonu ili neutronu.
Ako bi udaljenost između protona bila jednaka promjeru jezgre atoma, \(\left(\approx 10^{-15}\,\textrm{m}\right)\), rezidualna jaka sila
bila bi barem jednako jaka kao i elektromagnetska. Zbog rezidualne jake sile protoni unutar jezgre atoma drže se na okupu.
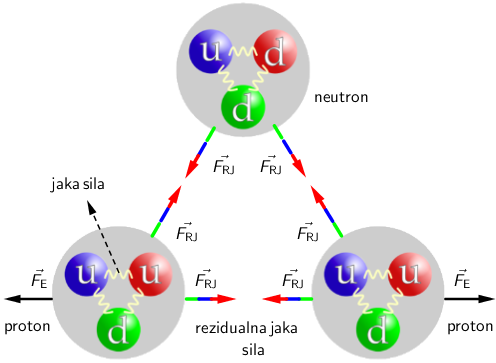
Točan odgovor je B.
25. zadatak
Tlak vodene pare iznad tekućine u ekspres-loncu pri temperaturi
30 o C
iznosi 105 Pa. Pretpostavite da se vodena para ponaša kao idealni plin
konstantnoga volumena. Tijekom zagrijavanja tlak vodene pare postigne vrijednost
1,26 ·105 Pa.
Kolika je temperatura postignuta u ekspres-loncu?
Odgovor: K
Izohorna promjena stanja plina (volumen plina je konstantan): \[\frac {P_{1}}{T_{1}}=\frac {P_{2}}{T_{2}}\]
- \(P_{1}\,\textrm{i}\,T_{1}\) - početni tlak i temperatura plina
- \(P_{2}\,\textrm{i}\,T_{2}\) - konačni tlak i temperatura plina
Temperaturu pretvorimo u kelvine: \[30\,^{\textrm{o}}\textrm{C}=303,15\,\textrm{K}\] \[\frac {P_{1}}{T_{1}}=\frac {P_{2}}{T_{2}}\] \[T_{2}=\frac {P_{2}}{P_{1}}\cdot T_{1}\] \[T_{2}=381,97\,K\]
26. zadatak
Svjetlovod indeksa loma 1,55 uronjen je u vodu indeksa loma 1,33.
Pod kojim se najvećim kutom smije savinuti svjetlovod tako da svjetlost ne iziđe iz svjetlovoda u vodu?
Odgovor: \(^{\textrm{O}}\)
Totalna refleksija
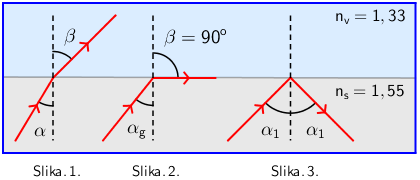
Zraka svjetlosti upada iz optički gušćeg (staklo) u optički rjeđe (voda) sredstvo.
-
Slika 1.
Zraka svjetlosti lomi se od okomice. \[n_{\textrm{s}}\,\textrm{sin}\,\alpha=n_{\textrm{v}}\,\textrm{sin}\,\beta\] -
Slika 2.
Povećanjem kuta upadanja \(\alpha\) povećava se i kut loma \(\beta\). Najveća vrijednost kuta loma je \(\beta=90^{\textrm{ o}}\). Kut upadanja za koji je kut loma 90 stupnjeva nazivamo granični kut totalne refleksije \(\alpha_{\textrm{g}}\). \[n_{\textrm{s}}\,\textrm{sin}\,\alpha_{\textrm{g}}=n_{\textrm{v}}\cdot 1\] \[\textrm{sin}\,\alpha_{\textrm{g}}=\frac{n_{\textrm{v}}}{n_{\textrm{s}}}\] -
Slika 3.
Ako je kut upadanja veći od graničnog kuta, zraka svjetlosti na granici stakla i vode reflketira se natrag u staklo. Tada je, prema zakonu refleksije, kut upadanja jednak kutu odbijanja.
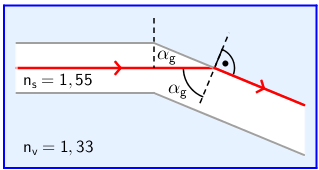
Iz slike se vidi da je kut pod kojim je savinut svjetlovod jednak graničnom kutu totalne refleksije.
\[\textrm{sin}\,\alpha_{\textrm{g}}=\frac{n_{\textrm{v}}}{n_{\textrm{s}}}=\frac{1,33}{1,55}\] \[\alpha_{\textrm{g}}=59,1\,^{\textrm{o}}\]
27. zadatak
Balon promjera 3,5 m napunjen je helijem. Ukupna masa balona i helija iznosi 9,2 kg. Balon je vezan užetom za tlo. Gustoća zraka iznosi 1,23 kg/m3. Koliki je iznos sile napetosti užeta?
Odgovor: N
Na balon u zraku djeluju:
- Sila teža: \(F_{\textrm{g}}=m\,g\)
- Uzgon zraka: \(F_{\textrm{u}}=\rho_{\textrm{z}}\,g\,V\)
Rezultanta te dvije sile napinje uže.
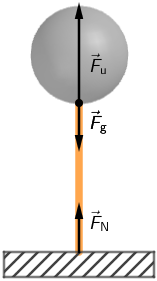
Napetost užeta: \[F_{\small{\textrm{N}}}=F_{\textrm{u}}-F_{\textrm{g}}\] \[F_{\small{\textrm{N}}}=\rho_{\textrm{z}}\,g\,V-m\,g\] Volumen balona: \[V=\frac{4}{3}\,r^{3}\,\pi=\frac{4}{3}\,\left(\frac{d}{2}\right)^{3}\,\pi=\frac{4}{3}\,\frac{d^{3}}{8}\,\pi\] \[V=\frac{d^{3}\pi}{6}\] \[F_{\small{\textrm{N}}}=\rho_{\textrm{z}}\,g\,\frac{d^{3}\pi}{6}-m\,g\] \[F_{\small{\textrm{N}}}=184,13\,\textrm{N}\]
28. zadatak
Kolika je korisnost toplinskoga stroja koji obavlja koristan rad iznosa 4800 J i spremniku niže temperature preda 2200 J topline?
Odgovor:
Toplinski stroj koji od toplijeg spremnika temperature \(T_{1}\) prima toplinu \(Q_{1}\), a hladnijem spremniku temperature \(T_{2}\) predaje toplinu \(Q_{2}\) obavlja koristan rad: \[W=Q_{1}-\left|Q_{2}\right|\] Korisnost takvog stroja: \[\eta=\frac{W}{Q_{1}}\]
Iz korisnog rada i predane topline odredimo primljenu toplinu: \[W=Q_{1}-\left|Q_{2}\right|\] \[Q_{1}=W+\left|Q_{2}\right|\] Korisnost stroja: \[\eta=\frac{W}{Q_{1}}=\frac{W}{W+\left|Q_{2}\right|}\] \[\eta=0,69\] ili \[\eta=69\, \%\]
29. zadatak
U jednostavnome modelu atoma vodika elektron kruži oko protona po stazi polumjera
2,12·10 -10 m.
Koliki je iznos brzine kruženja elektrona oko protona u navedenome modelu?
Rezultat zapišite u obliku znanstvenog zapisa s jednim decimalnim mjestom.
Odgovor: m/s
Polumjer prve kružnice prema Bohrovom modelu (atom se tada nalazi u osnovnom stanju): \[r_1=5,29\cdot{10}^{\mathbf{-}11}\ \textrm{m}\] Polumjere ostalih kružnica možemo lako izračunati: \[r_n=r_1{\cdot n}^2\] \[n=1,2,3,4,5\cdot\cdot\cdot\]
Brzina elektrona u osnovnom stanju: \[v_1=2,18\cdot{10}^6\ \textrm{m}/\textrm{s}\] Brzinu elektrona na bilo kojoj kružnici možemo jednostavno odrediti: \[v_n=\frac{v_1}{n}\] \[n=1,2,3,4,5\cdot\cdot\cdot\]
Više o Bohrovom modelu atoma možete saznati na poveznici Bohrov model atoma.
Najprije odredimo kvantni broj (redni broj staze): \[n=\sqrt{\frac{r_{n}}{r_{1}}}=\sqrt{\frac{2,12\cdot 10^{-10}}{5,29\cdot 10^{-11}}}=2\] Brzina elektrona u drugoj Bohrovoj kružnici je: \[v_n=\frac{v_1}{n}=\frac{2,18\cdot 10^{6}}{2}=1,09\cdot 10^{6}\,\textrm{m/s}\] U polje za odgovor upišite 1,09E6.
30. zadatak
Elektronski mikroskop koristi se razlikom potencijala 1 kV za ubrzanje elektrona iz mirovanja.
Zanemarivi su relativistički efekti.
Kolika je valna duljina elektrona u nastalome elektronskom snopu?
Rezultat zapišite u obliku znanstvenog zapisa s jednim decimalnim mjestom.
Odgovor: m
De Broglieva valna duljina: \[\lambda=\frac{h}{m\,v}=\frac{h}{p}\] Klasična kinetička energija elektrona (relativistički efekti su zanemareni): \[E_{\small{\textrm{K}}}=\frac{m\,v^{2}}{2}\] Električno polje obavilo je rad \(W=e\,U\) koji se pretvorio u kinetičku energiju elektrona: \[e\,U=\frac{m\,v^{2}}{2}\] Iz ovog izraza odredimo brzinu elektrona pa zatim i de Broglievu valnu duljinu.
\[E_{\small{\textrm{K}}}=\frac{m\,v^{2}}{2}\] \[E_{\small{\textrm{K}}}=\frac{m^{2}\,v^{2}}{2\,m}\] \[p^{2}=2\,m\,E_{\small{\textrm{K}}}\] \[p=\sqrt{2\,m\,E_{\small{\textrm{K}}}}\] \[E_{\small{\textrm{K}}}=e\,U\] \[p=\sqrt{2\,m\,e\,\small{U}}\] \[\lambda=\frac{h}{p}\] \[\lambda=\frac{h}{\sqrt{2\,m\,e\,\small{U}}}\] \[\lambda=3,9\cdot 10^{-11}\,\textrm{m}\] U polje za odgovor upišite 3,9E-11.
31. zadatak
Tijelo mase m1 = 2 kg miruje na horizontalnoj podlozi i uz pomoć opruge konstante elastičnosti k = 1000 N/m spojeno je za čvrsti oslonac kao što je prikazano na slici. Trenje između tijela i podloge je zanemarivo. U trenutku udara zrno metka mase m2 = 60 g ima brzinu v = 600 m/s u horizontalnome smjeru te se trenutno zabilo u tijelo i ostalo u njemu.
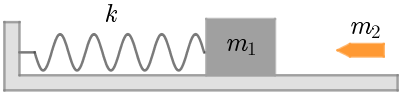
Kolika je amplituda titranja toga tijela nakon zabijanja zrna u njega?
Odgovor: m
Primijenom očuvanja količine gibanja oderedimo brzinu tijela nakon što se zrno u njega trenutno zabilo. Nakon toga tijelo sabija oprugu, brzina mu se smanjuje pa se smanjuje i kinetička energija. Budući da se tijelo udaljuje od početnog položaja, elastična potencijalna energija se povećava. U jednom se trnutku tijelo zaustavi, a to znači da se kinetička energija potpuno pretvorila u elastičnu potencijalnu energiju jer je trenje zanemarivo.
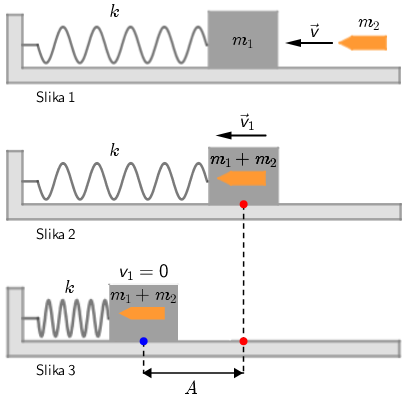
Slika 1
Primijenimo zakon očuvanja količine gibanja: Ukupna količina gibanja prije sudara jednaka je ukupnoj količini gibanja nakon sudara. Tijelo miruje pa je ukupna količina gibanja prije sudara jednaka količini gibanja zrna: \[m_{2}\,v\]
Slika 2
\[m_{2}\,v=\left( m_{1}+m_{2}\right)v_{1}\] Brzina tijela neposredno nakon što se zrno u njemu zaustavilo iznosi: \[v_{1}=\frac{m_{2}\,v}{m_{1}+m_{2}}=17,48\,\textrm{m/s}\] U tom trenutku tijelo se nalazi u ravnotežnom položaju (crveno obojena točka). Njegova kinetička energija je: \[E_{\small{\textrm{K}}}=\frac{1}{2}\left(m_{1}+m_{2}\right){v_{1}}^{2}\] Elastična potencijalna energija tijela u ravnotežnom položaju jednaka je nuli pa je ukupna energija: \[E_{1}=E_{\small{\textrm{K}}}=314,56\,\textrm{J}\]
Slika 3
Zbog djelovanja elastične sile opruge brzina tijela se smanjuje i u jednom trenutku tijelo se zaustavi. Taj položaj zovemo amplitudni položaj (plavo obojena točka). Kinetička energija jednaka je nuli, a elastična potencijalna energija je: \[E_{\small{\textrm{P}}}=\frac{1}{2}k\,A^{2}\] Ukupna energija u amplitudnom položaju jednaka je elastičnoj potencijalnoj energiji: \[E_{2}=E_{\small{\textrm{P}}}\] \[E_{2}=\frac{1}{2}k\,A^{2}\] Primijenimo zakon očuvanja energije: \[E_{2}=E_{1}\] Iz ovog izraza odredimo amplitudu harmonijskog titranjatitranja: \[A=\sqrt{\frac{2\,\small{E}_{\small{\textrm{K}}}}{k}}=0,79\,\textrm{m}\]
32. zadatak
Tijelu koje se gurne uz kosinu bez trenja početnom brzinom
v0 = 3 m/s
potrebna je jedna sekunda da stane.
Koliki je put prešlo tijelo prije zaustavljanja?
Odgovor: m
Gibanje tijela uz kosinu je jednoliko usporeno.
Brzina tijela:
\[v=v_{0}-a\,t\]
Put koji je tijelo prešlo:
\[s=v_{0}\,t-\frac{1}{2}a\,t^{2}\]
\[v=v_{0}-a\,t\] Kada se tijelo zaustavi, brzina mu je jednaka nuli: \[v_{0}-a\,t=0\] Iz ovog izraza odredimo akceleraciju: \[a=\frac{v_{\small{0}}}{t}= 3\,\textrm{m/s}^{2}\] Uvrštavanjem podataka lako odredimo prijeđeni put: \[s=v_{0}\,t-\frac{1}{2}a\,t^{2}=1,5\,\textrm{m}\]
33. zadatak
Učenik treba odrediti elektromotorni napon izvora ε i njegov unutarnji otpor Ru. Na raspolaganju ima voltmetar, ampermetar, promjenjivi otpornik i izvor. Složio je strujni krug kao što je prikazano na slici.
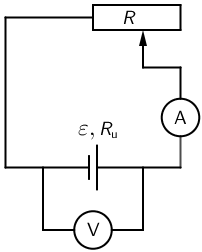
Kako bi odredio ε i
Ru
učenik treba napraviti dva mjerenja.
U prvome mjerenju ampermetar pokazuje 2 A,
a voltmetar 4,5 V.
U drugome mjerenju, nakon što se promijeni otpor na promjenjivome otporniku, ampermetar
pokazuje 1,5 A, a voltmetar 6 V.
Koliki su unutarnji otpor i elektromotorni napon izvora?
\(R_{\textrm{u}}=\) \(\Omega\)
\(\large{\varepsilon}\,\normalsize{=}\) V
Primijenite Ohmov zakon za cijeli strujni krug.
Ohmov zakon za cijeli strujni krug: \[I=\frac{\large{\varepsilon}}{R+R_{\textrm{u}}}\] Riješimo se razlomka: \[\large{\varepsilon}=\normalsize{}I\left(R+R_{\textrm{u}}\right)\] \[\large{\varepsilon}=\normalsize{I\,R+I\,R_{\textrm{u}}}\] \[U=I\,R\] \[\large{\varepsilon}=\normalsize{U+I\,R_{\textrm{u}}}\] Uvrstimo podatke iz prvog i drugog mjerenja: \[\large{\varepsilon}=\normalsize{4,5+2\,R_{\textrm{u}}}\qquad(1)\] \[\large{\varepsilon}=\normalsize{6+1,5\,R_{\textrm{u}}}\qquad(2)\] Izjednačimo desne strane izraza (1) i (2): \[4,5+2\,R_{\textrm{u}}=6+1,5\,R_{\textrm{u}}\] \[R_{\textrm{u}}=3\,\Omega\] Dobivenu vrijednost unutarnjeg otpora uvrstimo u izraz (1) ili (2): \[\large{\varepsilon}=\normalsize{10,5 \,\textrm{V}}\]
34. zadatak
Duga tanka žica postavljena je u beskonačnu zavojnicu koja ima 1000 navoja po metru svoje dužine paralelno s osi zavojnice.
Kroz žicu i zavojnicu prolaze struje iznosa I = 1 A .
Udaljenost žice od osi zavojnice iznosi 1 mm.
Koliki je iznos ukupnoga magnetskog polja na osi zavojnice?
Odgovor zapišite u obliku znanstvenog zapisa s jednim decimalnim mjestom.
Odgovor: T
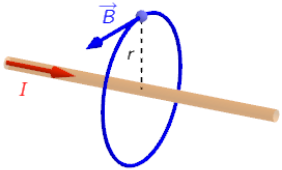
Smjer magnetskog polja ravne žice u nekoj točki silnice jednak je tangentni na silnicu u toj točki. Orijentaciju magnetskog polja odredimo pravilom desne ruke.
Iznos magnetskog polja ovisi o struji \(I\) kroz vodič i o udaljenosti \(r\) od vodiča:
\[B_{\small{\textrm{Ž}}}=\frac{\mu_{0}}{2\,\pi}\,\frac{I}{r}\]
Navedeni izraz vrijedi za beskonačno dugu ravnu žicu (ili za žicu konačne duljine u području koje je jako daleko od krajeva žice).
Konstantu \(\mu_{0}\) nazivamo permeabilnost vakuuma ili apsolutna permeabilnost:
\[\mu_{0}=4\,\pi \cdot 10^{-7}\,\frac{\textrm{T}\,\textrm{m}}{\textrm{A}}\]
Iznos magnetsko polje u središtu zavojnice duljine \(\ell\) sa \(N\) zavoja, kojom prolazi struja \(I\): \[B_{\small{\textrm{Z}}}=\mu_{0}\,\frac{NI}{\ell}\]
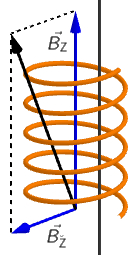
\[B_{\small{\textrm{Ž}}}=\frac{\mu_{0}}{2\,\pi}\,\frac{I}{r}\] \[B_{\small{\textrm{Ž}}}=2\cdot 10^{-4}\,\textrm{T}\] \[B_{\small{\textrm{Z}}}=\mu_{0}\cdot I\,\frac{N}{\ell}\] \[B_{\small{\textrm{Z}}}=1,257\cdot 10^{-3}\,\textrm{T}\] Magnetsko polje zavojnice \(B_{\small{\textrm{Z}}}\) leži na osi zavojnice, a magnetsko polje žice \(B_{\small{\textrm{Ž}}}\) prolazi kroz os zavojnice okomito na tu os. Smjerovi struja kroz žicu i zavojnicu nisu zadani, ali iznos rezultantnog magnetskog polja na osi zavojnice moguće je odrediti pomoću pravila za zbrajanje vektora (crno obojeni vektor na slici): \[B=\sqrt{B_{\small{\textrm{Z}}}^{\;2}+B_{\small{\textrm{Ž}}}^{\;2}}\] \[B=1,3\cdot 10^{-3}\,\textrm{T}\] U polje za odgovor upišite 1,3E-3.
35. zadatak
Kuglica je ovješena o tanku nerastezljivu nit čiju duljinu učenici pokusom trebaju odrediti.
35.1. Navedeni su skupovi pribora koji su učenicima na raspolaganju za izvođenje pokusa.
- nit, kuglica, stativ, vaga
- nit, kuglica, stativ, dinamometar
- nit, dvije kuglice različitih masa, stativ, vaga
- nit, kuglica, stativ, štoperica
U polje za odgovor napišite redni broj skupa pribora koji je učenicima minimalno potreban kako bi odredili nepoznatu duljinu niti.
Odgovor:
35.2. Četiri kuglice uz pomoć niti različitih duljina ovješene su kao što je prikazano na slici. Titranje pojedine kuglice prenosi se na preostale kuglice preko niti kojom su spojene. Učenik izvuče samo kuglicu K iz ravnotežnoga položaja okomito na ravninu gledanja i pusti je da se njiše.
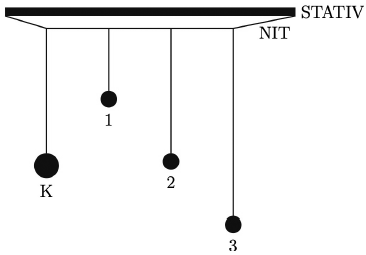
Navedena su moguća opažanja učenika o titranju kuglica.
- Kuglica 1 će zatitrati, a kuglice 2 i 3 neće uopće zatitrati.
- Kuglica 1 zatitrat će najvećom amplitudom, a kuglice 2 i 3 manjom.
- Kuglica 2 zatitrat će najvećom amplitudom, a kuglice 1 i 3 manjom.
- Kuglica 3 zatitrat će najvećom amplitudom, a kuglice 1 i 2 manjom.
U polje za odgovor napišite redni broj iskaza koji točno opisuje što će se od navedenoga dogoditi.
Odgovor:
35.3. Kuglica mase 15 g ovješena je o tanku nerastezljivu nit neke duljine i harmonijski titra tako da joj maksimalna brzina iznosi
12 cm/s.
Kolika je ukupna energija njihala?
Odgovor zapišite u obliku znanstvenog zapisa s dva decimalna mjesta.
E = J
35.1.
Ako malenu kuglicu ovješenu na nerastezljivu nit otklonimo iz ravnotežnog položaja za mali kut, ona će harmonijski titrati kao
matematičko (jednostavno) njihalo.
Period titranja matematičkog njihala:
\[T=2\,\pi\,\sqrt{\frac{\ell}{g}}\]
Iz ovog izraza možemo odrediti duljinu niti:
\[\ell=g\,\left(\frac{T}{2\,\pi} \right)^{2}\]
Osim stativa, niti i kuglice, potrebna nam je i štoperica kako bismo mogli izmjeriti period titranja.
35.2.
Kuglica K, koju smo pomaknuli iz ravnotežnog položaja i pustili ju harmonijski će titrati frekvencijom koju nazivamo vlastita frekvencija.
Vlastita frekvencija matematičkog njihala jednaka je:
\[f_{0}=\frac{1}{T}=\frac{1}{2\,\pi}\,\sqrt{\frac{g}{\ell}}\qquad(1)\]
Zbog titranja kuglice K njezina energija prelazi iz potencijalne u kinetičku i obrnuto. Ta se energija prenosi preko zajedničke niti na kuglice 1, 2 i 3.
Prijenos energije bit će veći kada je vlastita frekvencija kuglice K bliža vlastitoj frekvenciji neke od kuglica 1, 2 ili 3.
Ako postoji kuglica koja ima vlastitu frekvenciju jednaku kao i kuglica K, prijenos energije je najveći. Pojavu kada je prijenos energije s jednog na drugi
titrajni sustav najveći nazivamo rezonancija. Frekvenciju kojom tada titra neka od tri kuglice nazivamo
rezonantna frekvencija.
Vlastita frekvencija kuglice ovisi o duljini niti na koju je kuglica ovješena, što je vidljivo iz izraza (1). Iz slike vidimo da je kuglica 2 ovješena na nit
jednake duljine kao i kuglica K i zbog toga će kuglica 2 primiti najviše energije. Energija harmonijskog titranja proporcionalna je kvadratu amplitude pa će zato
kuglica 2 titrati većom amplitudom nego kuglice 1 i 3.
35.3.
Potencijalna energija matematičkog njihala:
\[E_{\small{\textrm{P}}}=\frac{1}{2}\,x^{2}\]
Konstanta \(k\) jednaka je:
\[k=\frac{m\,g}{\ell}\]
Kinetička energija matematičkog njihala:
\[E_{\small{\textrm{K}}}=\frac{1}{2}\,m\,v^{2}\]
Ukupna energija harmonijskog titranja jednaka je zbroju kinetičke i potencijalne energije:
\[E=E_{\small{\textrm{K}}}+E_{\small{\textrm{P}}}\]
U amplitudnom položaju kinetička energija jednaka je nuli, a potencijalna energija je najveća.
U ravnotežnom položaju potencijalna energija jednaka je nuli jer je \(x=0\), a kinetička energija jednaka je:
\[E=E_{\small{\textrm{K}}}=\frac{1}{2}\,m\,v_{0}^{\,2}\]
\[E=1,08\cdot 10^{-4}\,\textrm{J}\]
U polje za odgovor upišite 1,08E-4.