Ljetni rok 2017. godine
1. zadatak
Na slici je prikazan graf ovisnosti puta o vremenu za tijelo koje se giba.
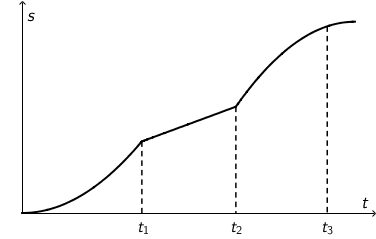
Koji graf prikazuje ovisnost brzine o vremenu za to tijelo?
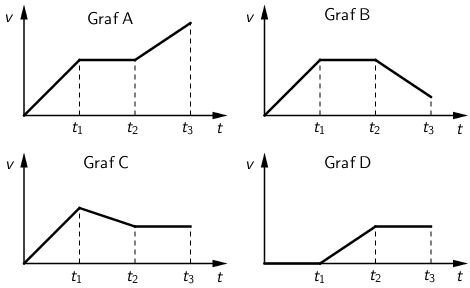
- A. Graf A
- B. Graf B
- C. Graf C
- D. Graf D
Pomoć potražimo na poveznici Gibanje po pravcu.
Klikom na Pomoć vidjeli smo kako izgledaju grafovi položaja i brzine u ovisnosti o vremenu za jednoliko, jednoliko ubrzano i jednoliko usporeno gibanje.
Iz crteža u zadatku zaključujemo:
- U intervalu vremena od \(0\) do \(t_{1}\) gibanje je jednoliko ubrzano.
- U intervalu vremena od \(t_{1}\) do \(t_{2}\) gibanje je jednoliko.
- U intervalu vremena od \(t_{2}\) do \(t_{3}\) gibanje je jednoliko usporeno.
2. zadatak
Tijelo se giba po kružnici polumjera \(r\) kutnom brzinom \(\omega\).
Koji od navedenih izraza vrijedi za centripetalnu akceleraciju \(a_{\textrm{cp}}\)?
- A. \(a_{\textrm{cp}}=\omega \, r^{2}\)
- B. \(a_{\textrm{cp}}=\omega/r^{2}\)
- C. \(a_{\textrm{cp}}=\omega^{2}\,r\)
- D. \(a_{\textrm{cp}}=\omega^{2}/r\)
U knjižici formula možemo pronaći izraz za centripetalnu akceleraciju: \[a_{\textrm{cp}}=\frac{v^{2}}{r}\] i kutnu brzinu: \[\omega=\frac{2\pi}{T}\] gdje je \(T\) ophodno vrijeme.
Čemu je jednaka obodna brzina tijela koje se giba jednoliko po kružnici?
\[a_{\textrm{cp}}=\frac{v^{2}}{r}\qquad(1)\] \[\omega=\frac{2\pi}{T}\qquad(2)\] Obodna brzina jednaka je: \[v=\frac{2r\pi}{T}\qquad(3)\] Usporedbom izraza (2) i (3) možemo zaključiti da je obodna brzina jednaka: \[v=\omega r\qquad(4)\] Uvrštavanjem izraza (4) u izraz (1) za centripetalnu akceleraciju dobijemo; \[a_{\textrm{cp}}=\omega^{2}r\]
3. zadatak
Na tijelo koje miruje počinju istodobno djelovati tri sile. Sila \(F_{1}=5\,\textrm{N}\) djeluje u smjeru istoka, sila \(F_{2}=7\,\textrm{N}\) u smjeru
zapada, a sila \(F_{3}=2\,\textrm{N}\) u smjeru sjevera.
Koja je od navedenih tvrdnja o gibanju toga tijela točna?
- A. Tijelo se giba jednoliko pravocrtno u smjeru sjeverozapada.
- B. Tijelo se giba jednoliko ubrzano u smjeru sjeverozapada.
- C. Tijelo se giba jednoliko pravocrtno u smjeru zapada.
- D. Tijelo se giba jednoliko ubrzano u smjeru zapada.
Nacrtajmo vektore sila koje djeluju na tijelo, odredimo njihovu rezultantu i primijenimo drugi Newtonov zakon.
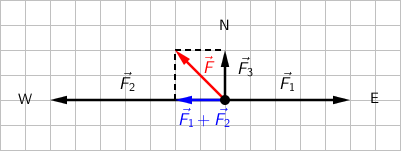
Rezultantnu silu \(\vec{F}\), koja je na crtežu označena crvenim vektorom, odredili smo vektorskim zbrajanjem sve tri sile.
Vidimo da je sila po iznosu konstantna i usmjerena prema sjeverozapadu pa će se zbog toga tijelo gibati jednoliko ubrzano u smjeru sjeverozapada.
4. zadatak
Tijelo se giba jednoliko ubrzano.
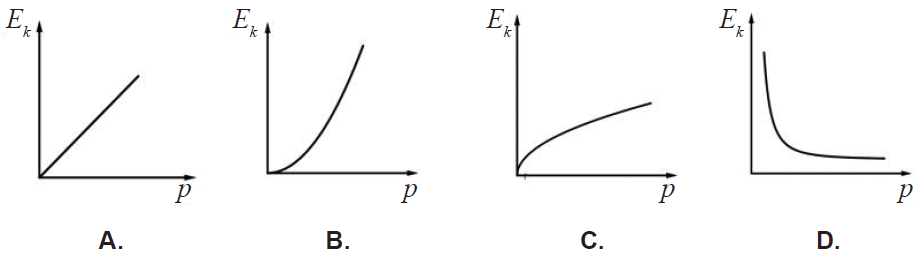
Koji graf prikazuje kako se kinetička energija tijela \(E_{\textrm{k}}\) mijenja ovisno o količini gibanja \(p\)?
Na početku je tijelo mirovalo.
- A. Graf A.
- B. Graf B.
- C. Graf C.
- D. Graf D.
U knjižici formula pronađimo izraze za kinetičku energiju i količinu gibanja tijela. Prikažimo kinetičku energiju kao funkciju količine gibanja.
Kinetičku energiju tijela prikazujemo izrazom: \[E_{\textrm{k}}=\frac{mv^{2}}{2}\qquad(1)\] Količinu gibanja prikazujemo izrazom: \[p=mv\qquad(2)\] Proširimo izraz (1) s \(m\) i uvrstimo izraz (2): \[E_{\textrm{k}}=\frac{p^{2}}{2m}\] Kinetička energija je kvadratna funkcija količine gibanja, što znači da je njezin graf prikazan parabolom. Od ponuđenih grafova paraboli jedino odgovara graf B.
5. zadatak
Prvo tijelo mase \(m\) bačeno je vertikalno uvis početnom brzinom \(v_{\textrm{o}}\) i postiglo je maksimalnu visinu \(H_{1}\). Drugo tijelo mase \(2\,m\)
bačeno je vertikalno uvis početnom brzinom \(3\,v_{\textrm{o}}\) i postiglo je maksimalnu visinu \(H_{2}\).
Koliki je omjer tih visina?
- A. \(9/4\)
- B. \(3/2\)
- C. \(3\)
- D. \(9\)
Primijenimo zakon očuvanja energije na oba tijela. Iz dobivenih jednadžbi odredimo omjer \(H_{2}/H_{1}\).
Prema zakonu očuvanja energije, kinetička tijela energija u trenutku izbacivanja jednaka je potencijalnoj energiji tijela u trenutku kada dostigne najveću visinu: \[\frac{mv^{2}}{2}=mgH\] Primjenimo taj zakon za prvo tijelo: \[\frac{mv_{0}^{2}}{2}=mgH_{1}\qquad(1)\] i za drugo: \[\frac{2m\cdot (3v_{0})^{2}}{2}=2mgH_{2}\qquad(2)\] Riješimo se nazivnika u oba izraza pa podijelimo izraz (2) izrazom (1): \[\frac{4mgH_{2}}{2mgH_{1}}=\frac{2m\cdot 9v_{0}^{2}}{mv_{0}^{2}}\] Nakon skraćivanja razlomaka dobijemo rezultat: \[H_{2}/H_{1}=9\]
6. zadatak
Zvijezda privlači komet silom \(F\) kada je on na udaljenosti \(r\) od središta zvijezde.
Kolikom silom zvijezda privlači komet kada joj se on približi na \(1/3\) početne udaljenosti?
- A. \(F/3\)
- B. \(F/9\)
- C. \(3\,F\)
- D. \(9\,F\)
Primijenimo Newtonov zakon gravitacije.
Bilo koja dva tijela u svemiru privlače se silom koja je proporcionalna njihovim masama, a obrnuto proporcionalna kvadratu udaljenosti između tijela.
 \[F_{\small{\textrm{G}}}=G\frac{Mm}{r^{2}}\]
Na 3 puta manjoj udaljenosti zvijezda će privlačiti komet \(3^{2}=9\) puta većom silom.
\[F_{\small{\textrm{G}}}=G\frac{Mm}{r^{2}}\]
Na 3 puta manjoj udaljenosti zvijezda će privlačiti komet \(3^{2}=9\) puta većom silom.
7. zadatak
Koji graf prikazuje produljenje metalne žice \(\Delta \ell\) ovisno o promjeni temperature \(\Delta t\)?
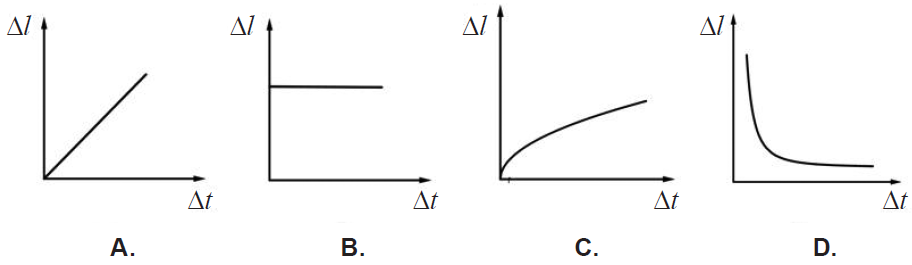
- A. Graf A.
- B. Graf B.
- C. Graf C.
- D. Graf D.
U knjižici formula pronađimo izraz za linearno termičko širenje.
Duljinu žice \(\ell\) pri temperaturi \(t\) možemo prikazati pomoću duljine žice \(\ell_{0}\) na temperaturi \(t_{0}\): \[\ell=\ell_{0}[1+\alpha (t-t_{0})]\qquad(1)\] Promjena temperature je \(\Delta t=t-t_{0}\). Promjenu duljine žice \(\Delta \ell=\ell-\ell_{0}\) odredimo iz izraza (1): \[\ell-\ell_{0}=\ell_{0}\alpha(t-t_{0})\] Uvažimo oznake za promjenu duljine i promjenu temperature: \[\Delta\ell=\ell_{0}\alpha \Delta t\] Promjena duljine žice linearna je funkcija promjene temperature pa je traženi graf pravac kroz ishodište.
8. zadatak
Koji izraz opisuje unutarnju energiju idealnoga plina?
- A. \(U=\frac{3}{2}N\,k\,T\)
- B. \(U=\frac{3}{2}p\,V\,T\)
- C. \(U=\frac{3}{2}N\,p\,V\)
- D. \(U=\frac{3}{2}n\,k\,T\)
U knjižici formula potražimo izraz za unutarnju energiju jednoatomnog idealnog plina.
Traženi izraz za unutarnju energiju jednoatomnog idealnog plina je: \[U=\frac{3}{2}N\,k\,T\]
9. zadatak
Koja od navedenih jednakosti vrijedi za kružni proces idealnoga plina?
- A. \(Q=\Delta U\)
- B. \(\Delta U=W\)
- C. \(Q=W\)
- D. \(W=0\)
Primijenimo prvi zakon termodinamike. U knjižici formula pronađimo matematički zapis tog zakona.
Prema prvom zakonu termodinamike jedan dio topline dovedene sustavu pretvara se u njegovu unutarnju energiju, a drugi se dio pretvara u rad koji sustav obavlja. \[Q=\Delta U+W\] U kružnom procesu idealnog plina početno stanje jednako je konačnom. Unutarnja energija je veličina stanja pa je na kraju jednog kružnog procesa \(\Delta U=0\). Prvi zakon termodinamike sada možemo zapisati kao: \[Q=W\]
10. zadatak
Naboj metalne kugle iznosi \(\texttt{-}8\cdot 10^{\texttt{-}19}\,\textrm{C}\).
Koja je od navedenih tvrdnja točna?
- A. Metalna kugla ima 5 elektrona više nego protona.
- B. Metalna kugla ima 5 elektrona manje nego protona.
- C. Metalna kugla ima 8 elektrona više nego protona.
- D. Metalna kugla ima 8 elektrona manje nego protona.
Izračunajmo broj elektrona koji odgovara naboju \(\texttt{-}8\cdot 10^{\texttt{-}19}\,\textrm{C}\).
Negativno nabijeno tijelo ima višeelektrona nego protona.
Izračunajmo broj elektrona koji odgovara zadanom naboju:
\begin{matrix}
\begin{align*}
&n=\frac{q}{e}\\
&n=\frac{\texttt{-}8\cdot 10^{\texttt{-}19}}{\texttt{-}1,6\cdot 10^{\texttt{-}19}}=5\\
\end{align*}
\end{matrix}
11. zadatak
Kondenzator kapaciteta \(C_{1}\) i kondenzator kapaciteta \(C_{2}\) spojeni su u seriju.
Koji je izraz točan za ukupan kapacitet \(C\) tako spojenih kondenzatora?
- A. \(C=C_{1}+C_{2}\)
- B. \(C=C_{1}=C_{2}\)
- C. \(C > C_{1}\) i \(C > C_{2}\)
- D. \(C < C_{1}\) i \(C < C_{2}\)
Kako određujemo ukupni kapacitet serijski spojenih kondenzatora?
Ukupni kapacitet serijsaki spojenih kondenzatora određujemo pomoću izraza: \[\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}\qquad(1)\] Iz izraza (1) zaključujemo: \begin{matrix} \begin{align*} &\frac{1}{C} > \frac{1}{C_{1}}\Rightarrow C < C_{1}\\ &\frac{1}{C} > \frac{1}{C_{2}}\Rightarrow C < C_{2} \end{align*} \end{matrix}
12. zadatak
Na slici je prikazan strujni krug.
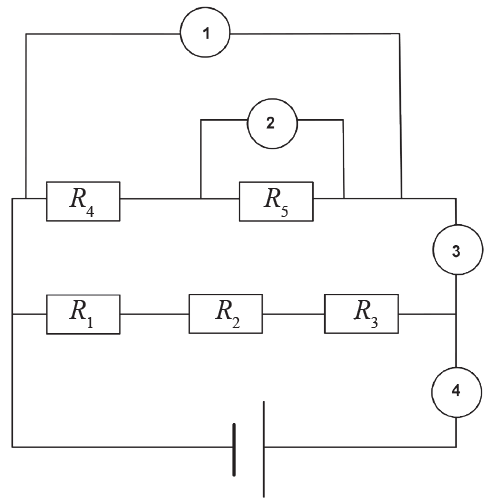
Na koji od položaja označenih brojevima 1, 2, 3 ili 4 treba spojiti ampermetar da bi se izmjerila električna struja koja prolazi otpornikom \(R_{5}\)?
- A. 1
- B. 2
- C. 3
- D. 4
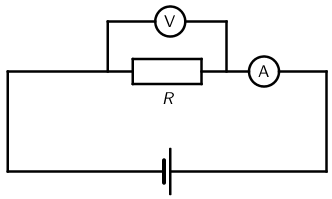
- Za mjerenje struje kroz neki otpor ampermetar spajamo serijski s otporom.
- Za mjerenje napona na nekom otporu voltmetar spajamo paralelno s otporom.
Iz sheme strujnog kruga u zadatku vidi se da će ampermetar u položaju 3 biti serijski spojen s otporom \(R_{5}\).
13. zadatak
Na električnoj žarulji s volframovom niti piše \(230\, \textrm{V}\) i \(100\, \textrm{W}\).
Koliki je otpor niti te žarulje?
- A. \(0,4\,\Omega\)
- B. \(2,3\,\Omega\)
- C. \(43,8\,\Omega\)
- D. \(529\,\Omega\)
Povežite izraz za snagu struje s Ohmovim zakonom za dio strujnog kruga.
Snagu električne struje prikazujemo izrazom: \[P=UI\qquad(1)\] Struju kroz žarulju odredimo pomoću Ohmovog zakona: \[I=\frac{U}{R}\qquad(2)\] Izraz (2) uvrstimo u izraz (1): \[P=\frac{U^{2}}{R}\qquad(3)\] Pomoću izraza (3) izračunajmo otpor žarulje: \[R=\frac{U^{2}}{P}=529\,\Omega\]
14. zadatak
Dugi ravni vodič kojim prolazi električna struja jakosti \(I\) nalazi se u homogenome magnetskom polju indukcije \(\overrightarrow{B}\) kao što je prikazano na slici.
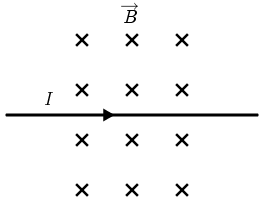
U kojemu smjeru djeluje magnetska sila na vodič?
- A. \(\Large\mathbf{\uparrow}\)
- B. \(\Large\mathbf{\downarrow}\)
- C. \(\Large\mathbf{\rightarrow}\)
- D. \(\Large\mathbf{\leftarrow}\)
Primijenimo pravilo desnog dlana.
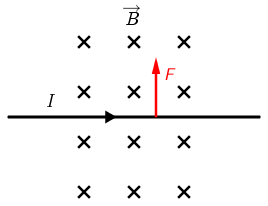
Palac desne ruke postavimo u smjer struje, a ispružene prste u smjer magnetskog polja. Sila je okomita na dlan i djeluje iz dlana.
15. zadatak
Koji graf prikazuje ovisnost kapacitivnog otpora \(R_{\textrm{c}}\) o periodu \(T\) u krugu izmjenične struje?
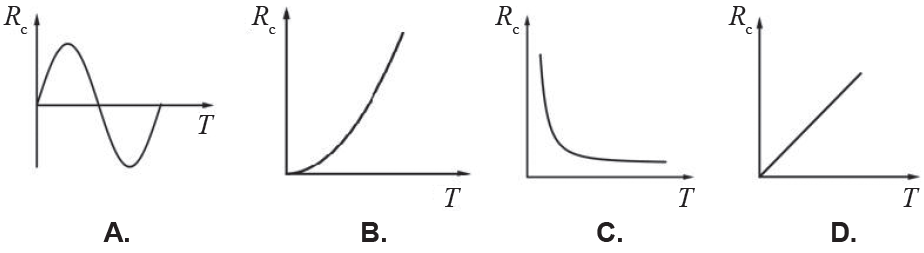
- A. Graf A.
- B. Graf B.
- C. Graf C.
- D. Graf D.
U knjižici formula pronađimo izraz za kapacitivni otpor.
Kako možemo prikazati kružnu frekvenciju \(\omega\) u ovisnosti o periodu?
Kapacitivni otpor: \[R_{\small{\textrm{C}}}=\frac{1}{C\omega}\qquad(1)\] Kružna frekvencija: \[\omega=\frac{2\pi}{T}\qquad(2)\] Uvrstimo izraz (2) u izraz (1): \[R_{\small{\textrm{C}}}=\frac{1}{2\pi C}T\] Kapacitivni otpor je linearna funkcija perioda. Graf ovakve linearne funkcije je pravac kroz ishodište.
16. zadatak
Dva tijela titraju harmonijski u vertikalnoj ravnini. U nekome je trenutku jedno tijelo u ravnotežnome položaju, a drugo u amplitudnome položaju.
Kolika je fazna razlika titranja tih dvaju tijela?
- A. \(0\)
- B. \(\pi/2\)
- C. \(\pi\)
- D. \(2\pi\)
Jednadžbu harmonijskog titranja možemo prikazati kao: \[y=A\,\textrm{sin}\left(\frac{2\pi}{T}t+\varphi_{0}\right )\]
- \(y\)-elongaciha titranja
- \(A\)-amplituda titranja
- \(T\)-period titranja
- \(t\)-vrijeme proteklo od početka titranja
Izraz u zagradi:
\[\varphi=\frac{2\pi}{T}t+\varphi_{0}\]
zove se faza titranja.
\(\varphi_0\) je početna faza.
Rješenje potražimo na poveznici Razlika faza.
17. zadatak
Dva koherentna vala šire se istodobno kroz isto sredstvo u istome smjeru.
Kolika mora biti razlika hoda između tih dvaju valova kada destruktivno interferiraju?
- A. \(\pi/2\)
- B. \(\lambda/2\)
- C. \(\pi\)
- D. \(\lambda\)
Pri destruktivnoj interferenciji valovi se maksimalno slabe.
Fazni uvjet za destruktivnu interferenciju je:
\[\Delta \varphi=\left ( 2k+1\right )\pi\qquad(1)\]
Razliku faza možemo prikazati i pomoću razlike hoda \(\Delta x\):
\[\Delta \varphi=\frac{2\pi}{\lambda}\Delta x\qquad(2)\]
Iz izraza(2) odredimo \(\Delta x\):
\[\Delta x=\frac{\lambda \Delta \varphi}{2\pi}\qquad(3)\]
U izraz (3) uvrstimo izraz (1):
\[\Delta x=\left (2k+1 \right )\frac{\lambda}{2}\qquad(4)\]
Izraz (4) ponekad nazivamo putni uvjet za destruktivnu interferenciju.
U izrazima (1) i (4) \(k\) može poprimiti vrijednosti:
\[k=0,\,1,\,2,\,3\,\cdot \cdot\cdot\]
Rješenje potražimo na poveznici Razlika hoda.
18. zadatak
Koja tvrdnja vrijedi za vektore električnoga polja \(\overrightarrow{E}\) magnetskoga polja \(\overrightarrow{B}\) elektromagnetskoga vala?
- A. Vektori \(\overrightarrow{E}\) i \(\overrightarrow{B}\) koji titraju u istoj fazi zatvaraju kut \(0^{\,\large\textrm{o}}\).
- B. Vektori \(\overrightarrow{E}\) i \(\overrightarrow{B}\) koji titraju u istoj fazi zatvaraju kut \(90^{\,\large\textrm{o}}\).
- C. Vektori \(\overrightarrow{E}\) i \(\overrightarrow{B}\) koji titraju u protufazi zatvaraju kut \(0^{\,\large\textrm{o}}\).
- D. Vektori \(\overrightarrow{E}\) i \(\overrightarrow{B}\) koji titraju u protufazi zatvaraju kut \(90^{\,\large\textrm{o}}\).
Širenje mehaničkih valova jednostavno je objasniti. Ako neku česticu sredstva (voda opruga, zrak, itd.) pokrenemo u titranje, energija se od te čestice širi prema drugim česticama. Kada ta energija dođe do neke druge čestice, i ona počinje titrati. Širenje titranja kroz neko sredstvo nazivamo valnim gibanjem, odnosno, kažemo da se sredstvom širi val.
Pokrenimo video.
Poznato je da se elektromagnetski valovi mogu širiti i kroz vakuum. U vakuumu nema čestice, pa što onda titra pri širenju elektromagnetskih valova?
Rješenje potražimo na poveznici Elektromagnetski val.
19. zadatak
Predmet je na udaljenosti \(f/2\) od divergentne leće.
Koja je tvrdnja točna za nastalu sliku predmeta?
- A. Slika je uvećana i virtualna.
- B. Slika je uvećana i realna.
- C. Slika je umanjena i virtualna.
- D. Slika je umanjena i realna.
Kakvu sliku predmeta daje divergentna leća?
Divergentna leća uvijek daje virtualnu, uspravnu i umanjenu sliku.
20. zadatak
Bijela svjetlost upada okomito na optičku rešetku.
Što vrijedi za kutove prvoga ogibnog maksimuma crvene i zelene boje?
- A. Kutovi su jednaki za obje valne duljine.
- B. Kut je veći za crvenu boju.
- C. Kut je veći za zelenu boju.
- D. Kutovi su proporcionalni zbroju valnih duljina.
Kada na optičku rešetku konstante \(d\) okomito upada svjetlost valne duljine \(\lambda\), dolazi do difrakcije ili ogiba svjetlosti. Na zastoru
koji se nalazi iza optičke rešetke vide se difrakcijski maksimumi (interferencijom se svjetlost pojačava) i minimumi
(interferencijom dolazi do slabljenja).
U knjižici formula pronađite jednadžbu za optičku rešetku.
Rješenje potražimo na poveznici Difrakcija na optičkoj rešetci.
21. zadatak
Kojom se od navedenih brzina treba gibati tijelo da za njega ne vrijede zakoni klasične mehanike?
- A. \(3\cdot 10^{4}\,\textrm{m}/\textrm{s}\)
- B. \(3\cdot 10^{5}\,\textrm{m}/\textrm{s}\)
- C. \(3\cdot 10^{6}\,\textrm{m}/\textrm{s}\)
- D. \(3\cdot 10^{7}\,\textrm{m}/\textrm{s}\)
Zakoni klasične fizike ne vrijede za brzine tijela koje su bliske brzini svjetlosti.
Od ponuđenih brzina u zadatku vidimo da je brzina \(3\cdot 10^{7}\,\textrm{m}/\textrm{s}\) svega deset puta manja od brzine svjetlosti.
22. zadatak
Foton energije \(5\,\textrm{eV}\) uzrokuje fotoelektrični učinak na metalu čiji je izlazni rad \(2\,\textrm{eV}\).
Kolika će biti maksimalna kinetička energija elektrona izbačenoga iz toga metala?
- A. \(2\,\textrm{eV}\)
- B. \(3\,\textrm{eV}\)
- C. \(5\,\textrm{eV}\)
- D. \(7\,\textrm{eV}\)
U knjižici formula pronađite jednadžbu kojom je Einstein objasnio zakonitosti fotoelektričnog učinka.
Energija fotona koji upadaju na površinu metala \(E_{f}\) pretvara se u rad potreban za izbacivanje elektrona iz metala i u kinetičku energiju elektrona izbačenih elektrona: \[E_{f}=W+E_{k}\] Najveća energija izbačenih elektrona jednaka je: \[E_{k}=E_{f}-W=5-2=3\,\textrm{eV}\] Jedinice energije nismo morali pretvarati u đžule jer su sve zadane u elektronvoltima, zbog čega je i dobiveni rezultat u elektronvoltima.
23. zadatak
Po čemu se izotop vodika \(_{1}^{3}\textrm{H}\) razlikuje od vodika \(_{1}^{1}\textrm{H}\)?
- A. Izotop \(_{1}^{3}\textrm{H}\) ima u jezgri jedan proton više od \(_{1}^{1}\textrm{H}\).
- B. Izotop \(_{1}^{3}\textrm{H}\) ima u jezgri jedan neutron više od \(_{1}^{1}\textrm{H}\).
- C. Izotop \(_{1}^{3}\textrm{H}\) ima u jezgri dva proton više od \(_{1}^{1}\textrm{H}\).
- D. Izotop \(_{1}^{3}\textrm{H}\) ima u jezgri dva neutrona više od \(_{1}^{1}\textrm{H}\).
Jezgru atoma simbolički prikazujemo kao \(_{Z}^{A}\textrm{X}\)
- \(Z\) - atomskim ili protonski broj (broj protona u jezgri)
- \(A\) - maseni ili nukleonski broj (broj nukleona u jezgri)
- \(X\) - simbol kemijskog elementa kojemu jezgra pripada
Izotop \(_{1}^{3}\textrm{H}\) u jezgri ima jedan proton i tri nukleona, odnosno \(N=3-1=2\) neutrona.
\(_{1}^{1}\textrm{H}\) u jezgri ima jedan proton, dok neutrona nema: \(N=1-1=0\).
24. zadatak
U zatvorenoj je posudi idealni plin mase \(m\) pri tlaku \(p\) i temperaturi \(T\).
Što će se dogoditi s tlakom plina ako se pri stalnoj temperaturi smanji početna masa plina?
- A. Smanjit će se.
- B. Povećat će se.
- C. Ostat će isti.
U knjižici formula pronađite jednadžbu stanja idealnog plina.
Jednadžbu stanja idealnog plina možemo prikazati kao: \[pV=nRT\qquad(1)\]
- \(p\) - tlak plina
- \(V\) - volumen plina
- \(n\) - broj molova
- \(R=8,314\,\textrm{J}\,\textrm{mol}^{\texttt{-}1}\,\textrm{K}^{\texttt{-}1}\) - opća plinska konstanta
- \(T\) - apsolutna temperatura
Napomena
Zadatak se može brže i jednostavnije riješiti.
Tlak plina je posljedica udaraca molekula o stijenke posude. Tlak će biti to veći što je veći broj molekula i što je veća njihova srednja
kinetička energija. Srednja kinetička energija proporcionalna je apsolutnoj temperaturi pa se ona neće mijenjati jer je temperatura stalna.
Prema tome, tlak plina pri stalnoj temperaturi ovisi samo o broju molekula koje udaraju u stijenke posude. Smanjenjem mase plina smanjit će
se i broj molekula pa prema tome i tlak plina.
25. zadatak
Na slikama su prikazana tri strujna kruga.
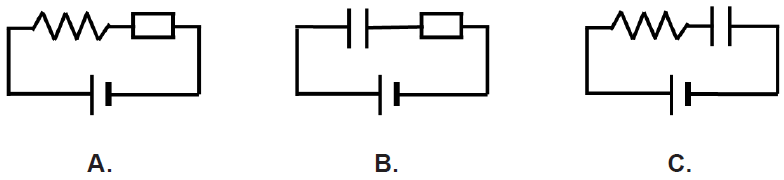
Koji strujni krug predstavlja \(LC\)-titrajni krug nakon odvajanja izvora napona i ponovnoga zatvaranja strujnoga kruga?
- A. Strujni krug A.
- B. Strujni krug B.
- C. Strujni krug C.
\(LC\) titrajni krug sastoji se od serijski spojenih zavojnice i kondenzatora.
Točnoj shemi \(LC\) titrajnog kruga odgovara shema ponuđena pod C.
26. zadatak
Kamen slobodno pada i udari u tlo brzinom \(50\,\textrm{m}/\textrm{s}\).
S koje je visine pao kamen? Zanemarite otpor zraka.
Odgovor:
Slobodni pad je jednoliko ubrzano gibanje prouzrokovano djelovanjem sile teže. Tijelo u početnom trenutku miruje na visini \(h\) iznad
površine Zemlje.
Pronađite u knjižici formula odgovarajući izraz.
Izraz za brzinu kod jednoliko ubrzanog gibanja prikazujemo kao: \[v^{2}={v_{0}}^{2}+2as\qquad(1)\] Kod slobodnog pada vrijedi:
- \(v_{0}=0\)
- \(a=g\)
- \(s=h\)
27. zadatak
U zatvorenoj je posudi s pomičnim klipom volumena \(0,5 \, \textrm{m}^{3}\) idealni plin pod tlakom \(2\cdot 10^{5} \,\textrm{Pa}\).
Koliki će biti tlak toga plina ako se volumen plina izotermno smanji za \(25\,\%\)?
Odgovor zapišite u obliku znanstvenog zapisa.
Odgovor: \(\textrm{Pa}\)
Ukoliko se ne možemo sjetiti izotermne promjene stanja plina, u knjižici formula pronađimo jednadžbu stanja idealnog plina: \[pV=nRT\qquad(1)\] Plin se nalazi u zatvorenoj posudi pa je broj molova konstantan: \(n=\textrm{konst}\). Pri izotermnoj promjeni stanja plina temperatura je konstantna: \(T=\textrm{konst}\). Prema tome, desna strana izraza (1) je konstantna: \(pV=\textrm{konst}\).
\begin{matrix} \begin{align*} &V_{1}=0,5\,\textrm{m}^{3}\\ &p_{1}=2\cdot 10^{5}\,\textrm{Pa}\\ &V_2=0,75\,V_{1} \qquad(\textrm{volumen se smanjio za 25 %})\\ &pV=\textrm{konst}\\ &p_{1}V_{1}=p_{2}V_{2}\\ &p_{2}=\frac{V_{1}}{V_{2}}p_{1}\\ &p_{2}=\frac{V_{1}}{0,75\,V_{1}}\cdot 2\cdot 10^{5}\\ &p_{2}=\frac{1}{0,75}\cdot 2\cdot 10^{5}\\ &p_{2}=2,67\cdot 10^{5}\,\textrm{Pa} \end{align*} \end{matrix} Rezultat unosimo kao 2,67E5 bez jedinice jer je ona navedena iza polja za odgovor.
28. zadatak
Koliki je ukupni otpor dvaju paralelno spojenih otpornika od \(2\, \Omega\) koji se nalaze u strujnome krugu?
Zanemarite otpor izvora.
Odgovor: \(\Omega\)
Iz kojeg se izraza može odrediti ukupan otpor dva paralelno spojena otpora?
\begin{matrix} \begin{align*} &\frac{1}{R}=\frac{1}{R_{1}}+\frac{1}{R_{2}}\\ &\frac{1}{R}=\frac{1}{2}+\frac{1}{2}=1\\ &R=\frac{1}{1}=1\,\Omega \end{align*} \end{matrix}
29. zadatak
Koliki mora biti kapacitet kondenzatora da bi uz zavojnicu induktivnosti \(3\, \textrm{mH}\)
period \(LC\)-titrajnoga kruga bio \(7\cdot 10^{\texttt{‒}5}\, \textrm{s}\)?
Odgovor upišite u obliku znanstvenog zapisa.
Odgovor: \(\textrm{F}\)
U knjižici formula pronađite izraz za period \(LC\) kruga i iz njega odredite kapacitet kondenzatora.
\begin{matrix} \begin{align*} &T=2\pi\sqrt{LC}\\ &C=\frac{T^{2}}{4\pi^{2}L}\\ &C=4,14\cdot 10^{\texttt{-}8}\,\textrm{F} \end{align*} \end{matrix} Rezultat unosimo u obliku 4,14E-8.
30. zadatak
Pri nuklearnoj reakciji oslobodi se \(10^{6} \,\textrm{kWh}\) energije.
Koliko iznosi defekt mase u toj reakciji?
Odgovor upišite u obliku znanstvenog zapisa.
Odgovor: \(\textrm{kg}\)
U knjižici formula pronađite izraz za energiju koja se oslobodi pri nuklearnoj reakciji i iz njega odredite defekt mase.
\begin{matrix} \begin{align*} &E=10^{6}\,\textrm{kWh}=10^{6}\cdot 10^{3}\cdot 3600\,\textrm{J}\\ &E=3,6\cdot 10^{12}\textrm{J}\\ &E=\Delta m\,c^{2}\\ &\Delta m=\frac{E}{c^{2}}\\ &\Delta m=4\cdot 10^{-5}\,\textrm{kg} \end{align*} \end{matrix} Rezultat unosimo u obliku 4E-5.
31. zadatak
Tijelo mase \(150\, \textrm{g}\) i brzine \(1\, \textrm{m}/\textrm{s}\) neelastično se sudari s tijelom mase \(250\, \textrm{g}\)
i brzine \(0,5\, \textrm{m}/\textrm{s}\). Tijela se gibaju po istome pravcu jedno prema drugomu.
Koliko iznosi kinetička energija tijela nakon sudara? Zanemarite trenje.
Odgovor zapišite u obliku znanstvenog zapisa.
Odgovor: \(\textrm{J}\)
Primjenom zakona očuvanja količine gibanja odredimo brzinu tijela nakon neelastičnog sudara.
Kako odrediti njihovu kinetičku energiju?
Rješenje potražimo na poveznici Očuvanje količine gibanja.
32. zadatak
U kalorimetru je \(2\, \textrm{dL}\) vode temperature \(100\,^{o}\textrm{C}\).
Nakon koliko će vremena sva voda iz kalorimetra ispariti ako je u kalorimetar uronjen grijač snage \(1000\, \textrm{W}\)?
Specifična toplina isparavanja vode iznosi \(2,2\cdot 10^{6}\,\textrm{J}/\textrm{kg}\), a gustoća vode \(1000\, \textrm{kg}/\textrm{m}^{3}\).
Zanemarite gubitke energije u okolinu.
Odgovor:
U knjižici formula podražite izraz za toplinu ispravanja.
Pomoću poznate snage grijača odredite potrebno vrijeme.
Toplinu isparavanja prikazujemo kao: \[Q_{\textrm{i}}=mr\] Masu vode izračunamo pomoću gustoće: \[m=\rho V\] Pomoću snage grijača: \[P=\frac{Q_{\textrm{i}}}{t}\] odredimo potrebno vrijeme: \[t=\frac{Q_{\textrm{i}}}{P}=\frac{\rho V r}{P}=440\,\textrm{s}\]
33. zadatak
Elektron se giba brzinom \(5\cdot 10^{6}\,\textrm{m}/\textrm{s}\) paralelno s ravnim vodičem kroz koji prolazi električna struja \(2\, \textrm{A}\).
Smjer struje i smjer brzine elektrona prikazani su na slici.
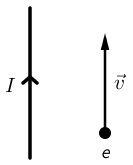
Kolikom silom vodič djeluje na elektron ako su oni udaljeni \(3\, \textrm{cm}\)?
Odgovor zapišite u obliku znanstvenog zapisa.
Odgovor:
U knjižici formula pronađite izraze za Lorentzovu silu i magnetsko polje oko dugog ravnog vodiča.
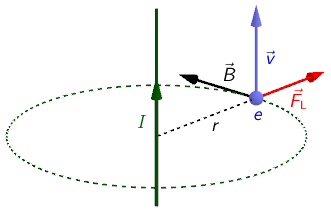
Nacrtajmo silnicu kojoj je polumjer okomit na vodič i koja prolazi točkom u kojoj se nalazi elektron. Smjer obilaska kružnice odredimo pravilom desne ruke. U točki u kojoj se nalazi elektron povucimo tangentu na kružnicu. Tako smo dobili smjer i orijentaciju magnetskog polja \(\overrightarrow{B}\).
Iznos magnetskog polja u toj je točki jednak: \[B=\frac{\mu_{0}}{2\pi}\frac{I}{r}=1,33\cdot 10^{\texttt{-}\,5}\,\textrm{T}\]
Magnetsko polje \(\overrightarrow{B}\) okomito je na brzinu kojom se giba elektron \(\overrightarrow{v}\) pa orijentaciju i smjer Lorentzove sile \(\overrightarrow{F_{\small{L}}}\) odredimo pravilom lijevog dlana jer je naboj elektrona \(e\) negativan.
Iznos Lorentzove sile jednak je: \[F_{\small{L}}=evB=1,07\cdot 10^{\texttt{-}17}\,\textrm{N}\] U polje za odgovor rezultat zapišimo kao 1,07E-17 N.
34. zadatak
Prazna plastična čaša mase \(100\, \textrm{g}\) pliva na vodi tako da je 1/4 volumena čaše uronjena u vodu.
Koliki se volumen ulja može uliti u čašu da ona još uvijek ne potone?
Gustoća ulja iznosi \(900\, \textrm{kg}/\textrm{m}^{3}\), a gustoća vode \(1000\, \textrm{kg}/\textrm{m}^{3}\).
Odgovor: \(\ell\)
Ako je prazna i ako je napunjena uljem, čaša pliva na površini vode, a to znači da su sila teža i uzgon u oba slučaja u ravnoteži.
Napišite odgovarajuće jednadžbe za oba slučaja i odredite volumen ulja u čaši.
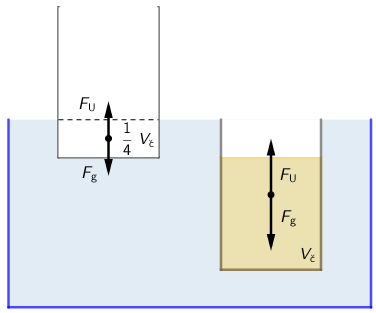
Kada je čaša prazna u vodu je uronjena četrtina njezina volumena. Uzgon koji djeluje na čašu i sila teža su u ravnoteži: \begin{matrix} \begin{align*} &F_{\textrm{u}}=F_{\textrm{g}}\\ &F_{\textrm{u}}=\rho_{\textrm{v}}\, g \cdot \frac{1}{4}\,V_{\textrm{č}}\\ &F_{\textrm{g}}=m_{\textrm{č}}\,g\\ &\rho_{\textrm{v}}\, g \cdot \frac{1}{4}\,V_{\textrm{č}}=m_{\textrm{č}}\,g\\ &m_{\textrm{č}}=\frac{1}{4}\,V_{\textrm{č}}\,\rho_{\textrm{v}}\qquad(1) \end{align*} \end{matrix}
Kada je u čašu uliveno ulje, čaša tek što ne potone, a to znači da je u vodu je uronjena cijelim svojim volumenom. Uzgon koji djeluje na čašu i sila teža su u ravnoteži: \begin{matrix} \begin{align*} &F_{\textrm{u}}=F_{\textrm{g}}\\ &F_{\textrm{u}}=\rho_{\textrm{v}}\, g \,V_{\textrm{č}}\\ &F_{\textrm{g}}=\left (m_{\textrm{č}}+m_{\textrm{u}}\right )\,g\\ &\rho_{\textrm{v}}\, g \,V_{\textrm{č}}=\left (m_{\textrm{č}}+m_{\textrm{u}}\right )\,g\\ &m_{\textrm{č}}+m_{\textrm{u}}=\rho_{\textrm{v}}\,V_{\textrm{č}}\qquad(2) \end{align*} \end{matrix}
Podijelimo izraz (2) izrazom (1): \[\frac{m_{\textrm{č}}+m_{\textrm{u}}}{m_{\textrm{č}}}=\frac{\rho_{\textrm{v}}\,V_{\textrm{č}}}{\frac{1}{4}\,V_{\textrm{č}}\,\rho_{\textrm{v}}}\] Skratimo razlomak na desnoj strani jednadžbe: \[\frac{m_{\textrm{č}}+m_{\textrm{u}}}{m_{\textrm{č}}}=4\] Iz ove jednadžbe za masu ulja dobijemo: \[m_{\textrm{u}}=3\,m_{\textrm{č}}\] Masu ulja prikažimo pomoću gustoće i volumena ulja: \[\rho_{\textrm{u}}\,V_{\textrm{u}}=3\,m_{\textrm{č}}\] Volumen ulja u čaši jednak je: \[V_{\textrm{u}}=\frac{3\,m_{\textrm{č}}}{\rho_{\textrm{u}}}=3,3\cdot 10^{\texttt{-}\,4}\,\textrm{m}^{3}=0,33\,\ell\]
35. zadatak
Dvije jednake male metalne kugle imaju naboje \(q_{1}\) i \(q_{2}\). Kada se nalaze na udaljenosti \(20\, \textrm{cm}\), između njih djeluje
odbojna sila od \(1,35\cdot 10^{\texttt{-}4}\,\textrm{N}\). Kugle se nakon toga dodirnu i zatim se ponovno vrate na udaljenost \(20\, \textrm{cm}\)
te tada između njih djeluje odbojna sila \(1,406\cdot 10^{\texttt{-}4}\,\textrm{N}\).
Koliko iznose naboji \(q_{1}\) i \(q_{2}\)?
Odgovore upišite u drugi stupac tablice.
| \(q_{1}\) | \(\textrm{nC}\) | |
| \(q_{2}\) | \(\textrm{nC}\) |
U knjižici formula pronađimo izraz za električni potencijal kugle: \[\varphi=k\frac{q}{r}\] Kada se kugle dodirnu, njihovi potecijali su jednaki: \begin{matrix} \begin{align*} &\varphi_{1}=k\frac{q}{r}\\ &\varphi_{2}=k\frac{q'}{r}\\ &\varphi_{1}=\varphi_{2}\Rightarrow q=q' \end{align*} \end{matrix} Naboji kugli nakon dodirivanja bit će jednaki. Prema zakonu očuvanja električnog naboja, ukupan naboaj prije dodira kugli mora biti jednak je njihovom ukupnom naboju nakon dodira: \[q+q=q_{1}+q_{2}\] Naboj kugli nakon dodira jednak je: \[q=\frac{1}{2}\left (q_{1}+q_{2} \right )\]
Napišimo Coulombov zakon kada su kugle udaljene \(r=0,2\,\textrm{m}\): \[F_{1}=k\frac{q_{1}q_{2}}{r^{2}}\qquad(1)\] Nakon što se kugle dodirnu i vrate na početnu udaljenost, sila između njih iznosi: \[F_{2}=k\frac{q^{2}}{r^{2}}\qquad(2)\] Naboj svake kugle jednak je: \[q=\frac{1}{2}\left (q_{1}+q_{2} \right )\qquad(3)\] Uvrstimo izraz (3) u izraz (2): \[F_{2}=k\frac{\left (q_{1}+q_{2} \right )^{2}}{4r^{2}}\qquad(4)\] Ako u jednadžbe (1) i (4) uvrstimo poznate podatke, dobivamo sustav dvije jednadžbe s dvije nepoznanice. Rješenja tog sustava su: \begin{matrix} \begin{align*} &q_{1}=20\,\textrm{nC}\\ &q_{2}=30\,\textrm{nC} \end{align*} \end{matrix}
36. zadatak
Na žici duljine \(17,5\, \textrm{m}\) može se izbrojiti osam čvorova stojnoga vala uključujući i krajeve žice. Izvor vala učini \(20\) potpunih
titraja u \(10\, \textrm{s}\).
Kolikom se brzinom širi val duž žice?
Odgovor:
Stojni val nastaje interferencijom dva jednaka vala koja se šire u suprotnom smjeru. Trbusi stojnog vala su čestice koje titraju maksimalnom elongacijom,
a čvorovi stojnog vala ne titraju.
Na stojni val koji nastaje titranjem žice učvršćene na oba kraja uvijek se na krajevima žice formiraju čvorovi.
Rješenje potražimo na poveznici Stojni val.
37. zadatak
Cezijevu pločicu obasjamo elektromagnetskim zračenjem valne duljine \(450\, \textrm{nm}\).
Kolika je razlika potencijala potrebna za zaustavljanje emisije elektrona iz pločice?
Izlazni rad za cezij iznosi \(2\, \textrm{eV}\).
Odgovor:
Primijenite jednadžu fotofekta.
Električno polje pri zaustavljanju elektrona izvrši rad. Čemu je taj rad jednak?
Primjenimo Einsteinovu jednadžbu fotoefekta: \[E_{\textrm{f}}=W+E_{\textrm{k}}\qquad(1)\] Za zaustavljanje elektrona električno polje mora izvršiti rad koji je jednak kinetičkoj energiji elektrona: \[eU=E_{\textrm{k}}\qquad(2)\] Uvrstimo izraz (2) u izraz (1): \[E_{\textrm{f}}=W+eU\] Razlika potencijala potrebna za zaustavljanje elektrona je: \[U=\frac{E_{\textrm{f}}-W}{e}\] Energija fotona jednaka je: \[E_{\textrm{f}}=\frac{hc}{\lambda}\] pa za razliku potencijala, odnosno napon električnog polja dobijemo: \[U=\frac{hc}{\lambda e}-\frac{W}{e}=0,76\,\textrm{V}\]