Ljetni rok 2021. godine
1. zadatak
Automobil se prvih 5 km giba stalnom brzinom 60 km/h, a sljedećih
5 km stalnom brzinom 100 km/h km/h.
Kolika je srednja brzina automobila tijekom cijeloga puta?
- A. 60 km/h
- B. 75 km/h
- C. 80 km/h
- D. 100 km/h
Pomoć potražite na poveznici Jednoliko pravocrtno gibanje.
2. zadatak
Na tijelo u mirovanju počnu istodobno djelovati tri sile jednakih iznosa kao što je prikazano dijagramom sila na slici.
Kako će se i u kojemu smjeru gibati tijelo uslijed djelovanja sila?
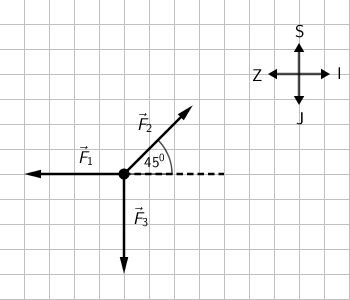
- A. jednoliko u smjeru sjeveroistoka
- B. jednoliko u smjeru jugozapada
- C. jednoliko ubrzano u smjeru sjeveroistoka
- D. jednoliko ubrzano u smjeru jugozapada
Ako na tijelo djeluje više sila, moramo odrediti rezultantu tih sila i zatim primijeniti temeljni zakon gibanja.
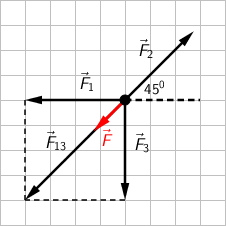
Iz crteža je vidljivo da smo prvo odredili rezultantu sila \(\vec{F}_{1}\) i \(\vec{F}_{3}\): \[\vec{F}_{13}=\vec{F}_{1}+\vec{F}_{3}\] Zatim odredimo rezultantu sila \(\vec{F}_{2}\) i \(\vec{F}_{13}\): \[\vec{F}=\vec{F}_{2}+\vec{F}_{13}\] Prema tome, tijelo (crni kružić) se, prema temeljnom zakonu gibanja, giba jednoliko ubrzano u smjeru jugozapada.
3. zadatak
Na slici je prikazana ovisnost sile koja djeluje na tijelo o prijeđenome putu. Sila djeluje na tijelo u smjeru gibanja tijela.
Koliki je obavljeni rad sile na tijelо?
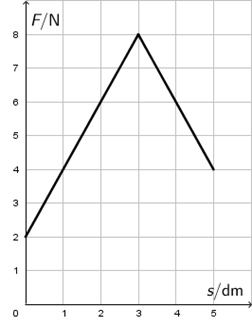
- A. 1,3 J
- B. 1,5 J
- C. 1,9 J
- D. 2,7 J
Pomoć potražite na poveznici Rad promjenjive sile.
Rad promjenjive sile najjednostavnije je odrediti grafički iz \(F,\,s\) grafa.
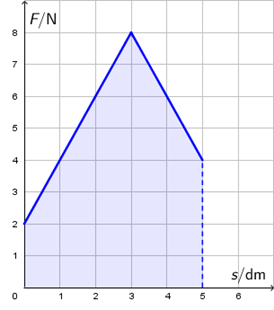
Obavljeni rad jednak je osjenčanoj površini (zbroj površina dva trapeza): \[W=\frac{2+8}{2}\cdot 0,3+\frac{8+4}{2}\cdot 0,2=2,7\, \textrm{J}\]
4. zadatak
Crvena i plava lopta istodobno su izbačene s vrha nebodera. Crvena lopta izbačena je u horizontalnome smjeru, a plava je ispuštena da slobodno pada.
Koja je od navedenih tvrdnja točna? Zanemarite otpor zraka.
- A. Obje lopte udaraju u tlo istodobno i različitim brzinama.
- B. Obje lopte udaraju u tlo istodobno i istim brzinama.
- C. Plava lopta udara u tlo prva, manjom brzinom od crvene lopte.
- D. Crvena lopta udara u tlo prva, većom brzinom od plave lopte.
Vrijeme za koje će lopta pasti na tlo ako ju izbacimo horizontalno s neke visine jednako je vremenu za koje će lopta pasti na tlo ako ju ispustimo s jednake visine da slobodno pada: \[t=\sqrt{\frac{2\,h}{g}}\]
Crvena i plava lopta past će na tlo nakon vremena: \[t_{1}=t_{2}=\sqrt{\frac{2\,h}{g}}\] Prema tome, lopte će na tlo pasti istodobno. Crvena lopta, koju smo izbacili horizontalno brzinom \(v_{0}\), past će na tlo brzinom \[v_{1}=\sqrt{v_{0}^{2}+g^{2}\,t_{1}^{2}}\] Plava lopta, koja slobodno pada, past će na tlo brzinom \[v_{2}=g\,t_{2}\] Usporedbom ove jednadžbe s prethodnom, zaključujemo da je \[v_{1} > v_{2}\] Crvena će lopta pasti na tlo većom brzinom od plave.
5. zadatak
Dva satelita masa \(m_{1}=2\,m_{2}\) gibaju se oko Zemlje po kružnim putanjama jednakih polumjera \(r_{1}=r_{2}\).
Koja od navedenih tvrdnja ne vrijedi za gibanje satelita?
- A. Na satelite djeluju jednake centripetalne sile.
- B. Sateliti imaju jednaka ophodna vremena.
- C. Sateliti se gibaju jednakim brzinama.
- D. Sateliti se gibaju jednakim centripetalnim ubrzanjima.
Pomoć potražite na poveznici Centripetalna akceleracija i sila.
Ulogu centripetalne sile ima gravitacijska sila kojom Zemlja mase \(M\) djeluje na satelite: \[F_{\textrm{c}}=G\frac{m\,M}{r^{2}}\] Budući da su polumjeri kružnih putanja jednaki, vidimo da će na satelit veće mase \(m\) djelovati veća centripetalna sila.
6. zadatak
Koja od navedenih tvrdnja ne vrijedi za toplinsko širenje metalne kugle pri zagrijavanju?
- A. Volumen je kugle veći što je veća promjena temperature.
- B. Promjena je volumena veća što je veći početni volumen kugle.
- C. Toplinsko širenje kugle ovisi o vrsti metala.
- D. Toplinskim širenjem kugle raste njezina gustoća.
Pomoć potražite na poveznici Volumno toplinsko širenje čvrstih tijela.
Porastom temperature kugle povećava se njezin volumen \(V\), dok se masa kugle \(m\) ne mijenja. Zbog toga će se gustoća kugle \[\rho=\frac{m}{V}\] smanjivati.
7. zadatak
Tri kuglice, olovna, bakrena i željezna, imaju jednaku masu \(m\) i zagrijane su do jednake temperature \(t_{1}\). Za specifične toplinske kapacitete kuglica
vrijedi \(c_{\textrm{olova}} < c_{\textrm{bakra}} < c_{\textrm{željeza}}\). U svaku od triju staklenih čaša napunjenih vodom temperature
\(t_{2} < t_{1}\) ubaci se po jedna kuglica. Početni volumen i temperatura vode u svim su čašama jednaki.
U kojoj će čaši konačna temperatura biti najveća? Zanemarite zagrijavanje staklenih čaša i okoline.
- A. u čaši s olovnom kuglicom
- B. u čaši s bakrenom kuglicom
- C. u čaši sa željeznom kuglicom
- D. u svim čašama jednaka
Toplina koju tijelo zagrijavanjem primi ili hlađenjem preda može se prikazati kao: \[Q=m\,c\,\Delta T\]
- \(m\) - masa tijela
- \(\Delta T\) - promjena temperature (može u kelvinima ili u stupnjevima Celzija)
Toplina nije oblik energije pohranjene u tijelu i zbog toga nije veličina koja ovisi o termodinamičkom stanju. Toplina je energija koju u termodinamičkom procesu izmjenjuju tijela. Zbog toga toplina ne ovisi o termodinamičkom stanju, nego o načinu prelaska iz početnog u konačno stanje. Zato kažemo da je toplina veličina procesa, a ne veličina stanja. Unutarnja energije je veličina stanja.
Kada zagrijanu kuglicu ubacimo u vodu koja ima manju temperaturu od kuglice, doći će do prijelaza topline \(Q\) s kuglice na vodu sve dok se temperatura kuglice ne izjednači s temperaturom vode (toplinska ravnoteža): \[Q=m\,c\,\Delta t\] Željezna kuglica ima najveći specifični toplinski kapacitet \(c\) pa će vodi predati najviše topline, zbog čega će i konačna temperatura biti najveća u čaši u koju je ubačena željezna kuglica.
8. zadatak
U zatvorenoj posudi s pomičnim klipom volumena \(V\) nalazi se idealni plin pod tlakom \(p\). Volumen je nakon izotermnoga širenja plina za
50 % veći od volumena \(V\).
Za koliko se posto smanji tlak plina?
- A. za 33 %
- B. za 45 %
- C. za 50 %
- D. za 67 %
Pomoć potražite na poveznici Izotermna promjena stanja plina.
Za izotermnu promjenu stanja idealnog plina vrijedi: \[p\,V=p_{1}\,V_{1}\] Konačni volumen je za 50 % veći od početnog: \[V_{1}=1,5\,V\] Uvrstimo \(V_{1}\) u prethodni izraz: \[p\,V=p_{1}\cdot 1,5\,V\Rightarrow p_{1}=\frac{p}{1,5}\] Tlak se smanjio za \[\Delta p=p-p_{1}=p-\frac{p}{1,5}=p\left(1-\frac{1}{1,5}\right)=0,33\,p\] Postotno smanjenje tlaka je: \[\frac{\Delta p}{p}\cdot 100=33\,\%\]
9. zadatak
Na slici je prikazan \(p,V\) graf za tri stanja idealnoga plina 1, 2 i 3. Svakomu stanju pripada unutarnja energija \(U_{1}\),\(U_{2}\) i \(U_{3}\).
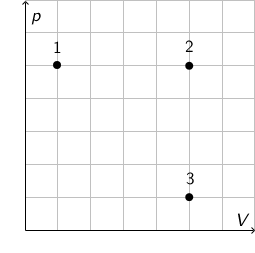
U kakvu su međusobnom odnosu unutarnje energije plina?
- A. \( U_{1}=U_{3} > U_{2}\)
- B. \( U_{1}=U_{2} > U_{3}\)
- C. \( U_{2}=U_{3} < U_{1}\)
- D. \( U_{1}=U_{3} < U_{2}\)
Pomoć potražite na poveznici Unutarnja energija idealnog plina.
Unutarnja energija jednoatomnog idealnog plina jednaka je: \[U=\frac{3}{2}\,N\,k\,T\] Iz jednadžbe stanja idealnog plina \[p\,V=N\,k\,T\] zaključujemo da unutarnju energiju možemo prikazati i kao: \[U=\frac{3}{2}\,p\,V\] Prema tome, unutarnja je energija proporcionalna umnošku \(p\,V\). Na osnovu zadanog grafa zaključujemo: \[U_{1}=U_{3}\] Iz grafa također zaključujemo da je unutarnja energija u stanju 2 veća nego u stanju 1 i stanju 3.
10. zadatak
Metalnu kuglu naboja 2 mC dotaknemo s drugom identičnom neutralnom kuglom.
Kolika sila djeluje između kugla nakon dodira kada ih razmaknemo na udaljenost 1 m u vakuumu?
- A. 9 N
- B. 36 N
- C. 9 kN
- D. 36 kN
Pomoć potražite na poveznici Coulombov zakon.
Pri dodiru nabijene i neutralne kugle dolazi do prijelaza elektrona s jedne na drugu kuglu. Ako je kugla nabijena negativno, elektroni će prelaziti s nabijene na neutralnu kuglu, a ako je nabijena pozitivnim nabojem, elektroni prelaze s neutralne na nabijenu kuglu. U oba slučaja kugle će biti električki nabijene i imat će jednak potencijal: \[\varphi=k\frac{q}{r}\] Obje kugle imaju jednak polumjer pa će im i naboj biti jednak. Zbog očuvanja električnog naboja ukupan naboj mora ostati 2 mC. Prema tome, naboj svake kugle je: \[q=1\, \textrm{mC}\] Ako kugle razmaknemo na udaljenost 1 m, one će međusobno djelovati električnom silom, koju prikazujemo Coulombovim zakonom: \[F=k\,\frac{q^{2}}{r^{2}}=9000\, \textrm{N}=9\, \textrm{kN}\]
11. zadatak
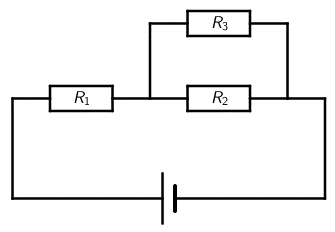
Na slici je prikazan spoj triju otpornika jednakih otpora koji spojeni imaju ekvivalentni otpor R.
Koliki je ekvivalentni otpor otpornika kada se iz spoja ukloni otpornik R3?
- A. R/2
- B. 3 R/4
- C. 4 R/3
- D. 3 R/2
Pomoć potražite na poveznici Spajanje otpora.
Odredimo ukupni otpor paralelno spojenih otpora: \[\frac{1}{R_{2,3}}=\frac{1}{R_{2}}+\frac{1}{R_{3}}\Rightarrow R_{2,3}=\frac{R_{2}\,R_{3}}{R_{2}+R_{3}}\] Sva tri otpora su jednaka: \(R_{1}=R_{2}=R_{3}\) pa je \[R_{2,3}=\frac{R_{1}^{2}}{2\,R_{1}}=\frac{R_1}{2}\] Ukupni otpor kruga na slici je: \[R=R_{1}+R_{2,3}=\frac{3}{2}\,R_{1}\] Ako uklonimo otpor \(R_{3}\), ukupni će otpor biti: \[R_{1,2}=R_{1}+R_{2}=2\,R_{1}\] Dijeljenjem ovog izraza s prethodnim dobijemo: \[\frac{R_{1,2}}{R}=2\,R_{1}\cdot\frac{2}{3\,R_{1}}\] \[R_{1,2}=\frac{4}{3}\,R\]
12. zadatak
Kako se može povećati magnetsko polje (magnetska indukcija) unutar zavojnice promjenom samo jedne veličine?
- A. smanjenjem struje kroz zavojnicu
- B. smanjenjem broja namotaja zavojnice
- C. povećanjem duljine zavojnice
- D. dodavanjem željezne šipke unutar zavojnice
Pomoć potražite na poveznici Magnetsko polje zavojnice kojom prolati struja.
Magnetsko polje unutar zavojnice duljine \(\ell\) kroz koju prolazi struja \(I\) i koja ima \(N\) zavoja prikazujemo izrazom: \[B=\mu_{0}\,\mu_{r}\,\frac{N\,I}{\ell}\] Iz ovog izraza i ponuđenih odgovora zaključujemo da je točan odgovor D jer je relativna permeabilnost željeza \(\mu_{r}=5000\). To znači da će se dodavanjem šipke od čistog željeza magnetsko polje u zavojnici povećati 5000 puta.
13. zadatak
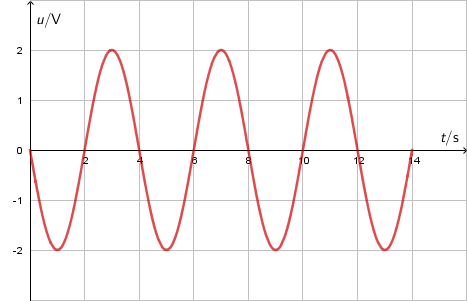
Na slici je prikazan graf ovisnosti trenutačnoga napona \(u\) o vremenu \(t\).
Koliko iznose maksimalni napon \(U_{0}\) i efektivna vrijednost napona \(U_{\textrm{ef}}\)?
- A. \(U_{0}=4\, \textrm{V},U_{\textrm{ef}}=2\,\sqrt 2\, \textrm{V}\)
- B. \(U_{0}=2\, \textrm{V},U_{\textrm{ef}}=\sqrt 2\, \textrm{V}\)
- C. \(U_{0}=2\, \textrm{V},U_{\textrm{ef}}=1/\sqrt 2\, \textrm{V}\)
- D. \(U_{0}=\sqrt 2\, \textrm{V},U_{\textrm{ef}}= 2\, \textrm{V}\)
Pomoć potražite na poveznici Izmjenični napon i struja.
Maksimalni napon očitamo iz grafa: \[U_{0}=2\, \textrm{V}\] Efektivni napon je: \[U_{\textrm{ef}}=\frac{U_{0}}{\sqrt 2}=\sqrt 2\, \textrm{V}\]
14. zadatak
Na slici je prikazana metalna žica koja se giba u homogenome magnetskom polju.
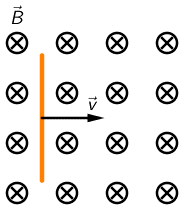
Što se događa s induciranim naponom na krajevima žice kada iznos brzine raste?
- A. Povećava se.
- B. Smanjuje se.
- C. Ostaje jednak.
- D. Jednak je nuli.
Pomoć potražite na poveznici Inducirani napon u ravnoj žici.
Na krajevima vodiča duljine \(\ell\), koji se u magnetskom polju \(B\) giba brzinom \(v\), okomito na magnetsko polje, inducira se napon: \[U_{\textrm{i}}=B\,\ell\, v\] Kada se iznos brzine povećava, povećavat će se i inducirani napon.
15. zadatak
Na slici je prikazana negativno nabijena metalna kugla.

Koje je orijentacije vektor elektrostatičkoga polja \(\vec{E}\) u točki T?
- A. \(\rightarrow\)
- B. \(\gets\)
- C. \(\uparrow\)
- D. \(\downarrow\)
Orijentacija električnog polja u nekoj točki jednaka je orijentaciji gibanja pozitivnog naboja u toj točki.
16. zadatak
Tijelo mase \(m\) pričvršćeno je na elastičnu oprugu i harmonijski titra amplitudom \(A\).
Kolika je ukupna energija titranja sustava ako se masa tijela poveća tri puta, a amplituda titranja ostane jednaka?
- A. tri puta manja
- B. jednaka kao i prije
- C. tri puta veća
- D. devet puta veća
Pomoć potražite na poveznici Pretvorbe energije pri harmonijskom titranju.
Ukupna energija harmonijskog titranja jednaka je zbroju kinetičke i elastične potencijalne energije u bilo kojem trenutku: \[E=E_{\textrm{k}}+E_{\textrm{ep}}\] U trenutku kada se tijelo nađe u amplitudnom položaju, njegova je kinetička energija jednaka nuli (tijelo na trenutak zastane) pa je ukupna energija jednaka elastičnoj potencijalnoj energiji: \[E=E_{\textrm{ep}}=\frac{1}{2}\,k\,A^{2}\] Ukupna energija harmonijskog titranja ne ovisi o masi tijela pričvršćenog na oprugu, nego samo o amplitudi titranja.
Napomena
U trenutku kada se tijelo nađe u ravnotežnom položaju njegova je elastična potencijalna energija jednaka nuli pa je ukupna energija jednaka
kinetičkoj energiji koja je maksimalna:
\[E=E_{\textrm{k}}=\frac{1}{2}\,m\,v_{0}^{2}\]
Ukupna mehanička energija je očuvana pa je
\[E_{\textrm{ep,maks}}=E_{\textrm{k,maks}}\]
17. zadatak
Koji od navedenih primjera sadrži isključivo mehaničke valove?
- A. zvuk, svjetlost, val na površini vode
- B. zvuk, val na površini vode, potresni val
- C. svjetlost, mikrovalovi, val na žici gitare
- D. radiovalovi, val na žici gitare, mikrovalovi
Pomoć potražite na poveznici Primjene leća.
Svjetlost, mikrovalovi i radiovalovi su primjeri elektromagnetskih valova. Točan odgovor je B.
18. zadatak
Koji crtež prikazuje virtualnu sliku S koja nastaje kada predmet P stavimo ispred ravnoga zrcala?
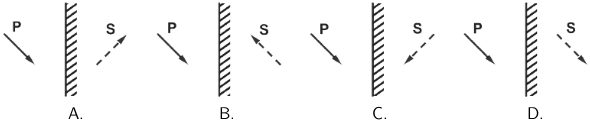
- A. Crtež A.
- B. Crtež B.
- C. Crtež C.
- D. Crtež D.
Pomoć potražite na poveznici Ravno zrcalo.
Ravno zrcalo daje virtualnu sliku realnog predmeta. Slika i predmet su jednako veliki i jednako orijentirani (ako je predmet uspravan, uspravna je i slika; ako je predmet obrnut, obrnuta je i njegova slika). Slika i predmet su simetrični u odnosu na zrcalo.
19. zadatak
Kako se od nepolarizirane svjetlosti može dobiti potpuno polarizirana svjetlost?
- A. lomom na optičkoj prizmi
- B. ogibom na optičkoj rešetki
- C. refleksijom na površini vode
- D. refleksijom na zrcalu
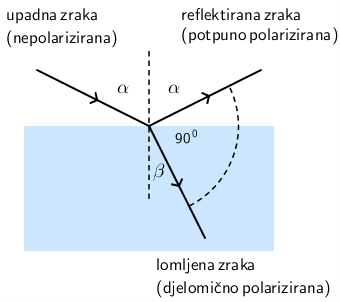
Ako je kut između reflektirane i lomljene zrake 90 stupnjeva, reflektirana zraka je potpuno polarizirana, a lomljena djelomično polarizirana.
Točan odgovor je C.
20. zadatak
Na slici je prikazan prolazak svjetlosti iz optičkoga sredstva indeksa loma \(n_{1}\) u optičko sredstvo indeksa loma \(n_{2}\).
Koja od ponuđenih slika ispravno prikazuje prolazak svjetlosti ako je \(n_{1} < n_{2}\)?
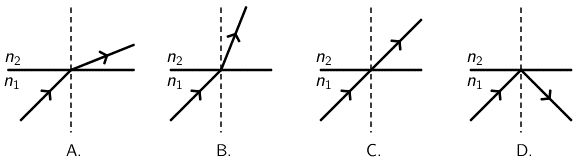
- A. Slika A.
- B. Slika B.
- C. Slika C.
- D. Slika D.
Pomoć potražite na poveznici Stojni val na napetoj žici i u stupcu zraka.
Kada zraka svjetlosti prelazi iz sredstva manjeg indeksa loma u sredstvo većeg indeksa loma (iz optički rjeđeg u optički gušće sredstvo), ona se lomi prema okomici.
21. zadatak
Konstanta optičke rešetke iznosi \(2\, \mu \textrm{m}\).
Koliko zareza po duljini ima zadana optička rešetka?
- A. 500 zareza po milimetru
- B. 500 zareza po centimetru
- C. 500 zareza po decimetru
- D. 500 zareza po metru
Pomoć potražite na poveznici Ogib svjetlosti na optičkoj rešetki.
Konstanta optičke rešetke \(d\) jednaka je udaljenosti između dvije susjedne pukotine (ili između dva susjedna zareza): \[d=\frac{L}{N}\] \[\frac{N}{L}=\frac{1}{d}=\frac{1}{2\cdot 10^{-6}\,\textrm{m}}=\frac{500000}{\textrm{m}}=\frac{500}{\textrm{mm}}\] \(N\) je broj zareza, a \(L\) duljina optičke rešetke.
22. zadatak
Koja je od navedenih tvrdnja točna za Bohrov model atoma?
- A. Elektron je najviše vezan za jezgru ako se nalazi u osnovnome stanju.
- B. Elektron je najviše vezan za jezgru ako se nalazi na energijskoj razini atoma \(n=4\).
- C. Elektron koji se nalazi u osnovnome stanju ima potencijalnu energiju \(E_{\textrm{p}}=–13,6\, \textrm{eV}\).
- D. Elektron koji se nalazi u osnovnome stanju ima kinetičku energiju \(E_{\textrm{k}}=–13,6\, \textrm{eV}\).
Pomoć potražite na poveznici Bohrov model atoma.
Prema Bohrovom modelu energija vodikovog atoma može poprimiti vrijednosti: \[E_{\textrm{n}}=\frac{E_{1}}{n^{2}}\] Energija osnovnog stanja vodikovog atoma \[E_{1}=-13,6\,\textrm{eV}\] po iznosu je najveća (energija ionizacije - energija koju treba dovesti vodikovom atomu da bi došlo do ionizacije).
23. zadatak
Što se emitira pri gama-raspadu?
- A. jezgre helija
- B. brzi elektroni
- C. pozitroni
- D. elektromagnetski valovi
- Alfa-raspad: emitiraju se jezgre helije \(\left (_{2}^{4}\,\textrm{He}-\textrm{alfa čestice}\right )\)
- Beta-raspad: emitiraju se brzi elektroni \(\left (_{-1}^{\;\;0}\,\textrm{e}\right )\) ili pozitroni \(\left (_{+1}^{\;\;0}\,\textrm{e}\right )\)
- Gama-raspad: emitiraju se elektromagnetski valovi \(\left (\gamma-\textrm{fotoni ili gama zrake}\right)\)
Gama zrake su elektromagnetski valovi. Točan odgovor je D.
24. zadatak
Žarulja emitira elektromagnetske valove pri temperaturi od 3000 K.
Kojemu dijelu spektra elektromagnetskoga zračenja pripada valna duljina kojoj odgovara maksimalna energija zračenja žarulje?
Pretpostavite da žarulja zrači kao apsolutno crno tijelo.
- A. infracrvenomu
- B. vidljivomu
- C. ultraljubičastomu
Pomoć potražite na poveznici Elektromagnetski spektar.
Wienov zakon: \[\lambda_{\textrm{max}}\cdot T=b\] \[\lambda_{\textrm{max}}=\frac{b}{T}=\frac{2,89\cdot 10^{-3}}{3000}=963,3\,\textrm{nm}\] Izračunata valna duljina odgovara infracrvenom dijelu spektra elektromagnetskog zračenja.
25. zadatak
Kroz dugu cijev stalnoga poprečnog presjeka zrak struji stalnom brzinom \(v\).
Kako se promijeni statički tlak u cijevi ako se poveća brzina strujanja zraka?
- A. Smanji se.
- B. Ostane jednak.
- C. Poveća se.
Pomoć potražite na poveznici Bernoullijeva jednadžba.
Prema Bernoullijevoj jednadžbi \[p+\frac{\rho\,v^{2}}{2}=\textrm{konst.}\] ukupni tlak (zbroj statičkog i dinamičkog tlaka) je konstantan. Povećanjem brzine dinamički tlak se poveća zbog čega se statički tlak mora smanjiti.
26. zadatak
Automobil krene iz mirovanja po ravnoj cesti stalnim ubrzanjem iznosa 1 m/s2.
Kolika je brzina automobila nakon 98 metara?
Odgovor: m/s
Pomoć potražite na poveznici: Jednoliko ubrzano pravocrtno gibanje.
Brzinu kod jednoliko ubrzanog pravocrtnog gibanje možemo odrediti iz izraza: \[v^{2}=v_{0}^{2}+2\,a\,s\] Početna brzina jednaka je nuli pa je brzina nakon 98 metara: \[v=\sqrt{2\,a\,s}=14\,\textrm{m}/\textrm{s}\]
27. zadatak
Koliko je molekula helija u balonu promjera 50 cm na temperaturi 27 0C i tlaku 1,01 bar? Pretpostavite da je balon sfernoga oblika, a helij idealni plin.
Odgovor:
Pomoć potražite na poveznici: Jednadžba stanja idealnog plina.
1 bar = 105 Pa
Iz jednadžba stanja idealnog plina:
\[p\,V=N\,k\,T\]
odredimo broj molekula:
\[N=\frac{p\,V}{k\,T}\]
Volumen balona je:
\[V=\frac{4}{3}\,r^{3}\,\pi=0,065\,\textrm{m}^{3}\]
\[N=\frac{1,01\cdot 10^{5}\cdot 0,065}{1,38\cdot 10^{-23}\cdot 300,15}=1,58\cdot 10^{24}\]
28. zadatak
Koliki je električni potencijal na udaljenosti 75 cm od točkastoga naboja +2 nC?
Odgovor: V
Izraz za potencijal točkastog naboja u vakuumu \(\left (\varepsilon_{r}=1\right )\) nalazi se u knjižici formula: \[\varphi=k\frac{q}{r}\]
\[\varphi=k\frac{q}{r}=9\cdot 10^{9}\,\frac{2\cdot 10^{-9}}{0,75}=24\,\textrm{V}\]
29. zadatak
Na slici je prikazana ovisnost elongacije tijela koje harmonijski titra o vremenu.
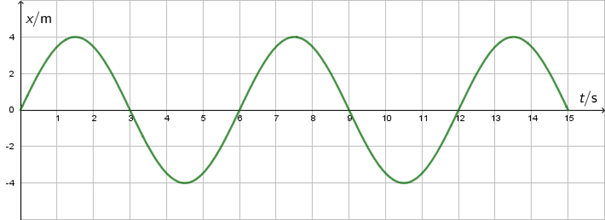
Kolika je maksimalna brzina titranja tijela?
Odgovor: m/s
U knjižici formula pronađemo maksimalnu brzinu harmonijskog titranja: \[v_{0}^{\,}=\frac{2\,A\,\pi}{T}\]
Iz grafa odredimo amplitudu \[A=4\,\textrm{m}\] i period \[T=6\,\textrm{s}\] Izračunamo najveću brzinu harmonijskog titranja: \[v_{0}^{\,}=\frac{2\,A\,\pi}{T}=4,19\,\frac{\textrm{m}}{\textrm{s}}\]
30. zadatak
Koja najmanja frekvencija elektromagnetskoga vala izaziva emisiju fotoelektrona iz metala čiji je izlazni rad 4 eV?
Odgovor: Hz
Pomoć potražite na poveznici Fotoelektrični učinak.
Energija fotona koji padaju na metal pretvara se u izlazni rad i kinetičku energiju fotoelektrona: \[E_{\textrm{f}}=W_{\textrm{i}}+E_\textrm{k}\] Energija fotona jednaka je \[E_\textrm{f}=h\,f\] Fotoelektrični učinak počinje se opažati pri graničnoj frekvenciji za koju je: \[E_\textrm{k}=0;h\,f=W_\textrm{i}\] \[f=\frac{W_{\textrm{i}}}{h}=\frac{4\cdot 1,6\cdot 10^{-19}}{6,626\cdot 10^{-34}}=9,66\cdot 10^{14}\,\textrm{Hz}\]
31. zadatak
Na sanduk djelujemo stalnom silom 10 N pod kutom 300 prema ravnini podloge kao što je prikazano na slici.
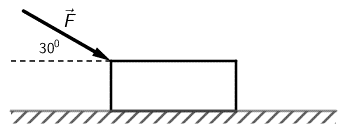
Koliko iznosi sila trenja ako se sanduk po podlozi giba stalnom brzinom?
Odgovor: N
Odredimo rezultantu sila koje djeluju na tijelo. Kolika je rezultantna sila ako se tijelo giba stalnom brzinom?
Na tijelo u horizontalnom smjeru djeluje horizontalna komponenta sile \(\vec{F}\) i sila trenja \(\vec{F}_\textrm{t}\).
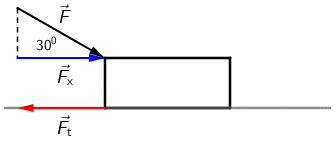
Iz crteža vidimo da je horizontalna komponenta sile jednaka \[F_{x}=F\cdot \textrm{cos}\,30^{0}=8,66\,\textrm{N}\] Translatirajmo obje sile u jednu točku.

Tijelo se giba jednolikom brzinom po horizontalnoj podlozi, a to znači da je rezultantna sila u horizontalnom smjeru jednaka nuli, odnosno, te dvije sile imaju jednak iznos. \[F_{\textrm{t}}=F_{x}=8,66\,\textrm{N}\]
32. zadatak
Koliku snagu mora imati grijač kako bi 250 g vode temperature 100 0C
isparilo za 1 h ako se sva energija grijača upotrebljava za zagrijavanje vode?
Specifična toplina isparavanja vode je 2,26 MJ/kg.
Odgovor: W
Pomoć potražite na poveznici: Promjena agregatnih stanja tvari.
Specifična toplina isparavanja: \[Q_{\textrm{i}}=r\,m\] Snaga grijača jednaka je energiji koju grijač oslobodi u jedinici vremena: \[P=\frac{E}{t}\] Energija grijača pretvara se u toplinu potrebnu za isparavanje vode: \(E=Q\). \[P=\frac{Q}{t}=\frac{m\,r}{t}=\frac{0,25\cdot 2,26\cdot 10^{6}}{3600}=156,94\,\textrm{W}\]
33. zadatak
Dva točkasta naboja Q1 = +2 nC i
Q2 = -4 nC smještena su u zraku na udaljenosti
45 cm.
Na kojoj je udaljenosti od Q1 duž spojnice naboja ukupno električno polje nula?
Odgovor: cm
Pomoć potražite na poveznici Električno polje točkastog naboja, sfere i kugle.
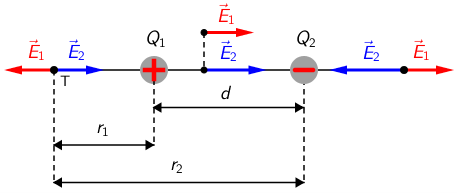
Rezultantno električno polje u nekoj će točki biti jednako nuli ako je iznos polja kojega stvara naboj Q1 jednak iznosu polja kojega stvara naboj Q2, a orijentacije polja su suprotne: \[\vec{E}_{2}=-\vec{E}_{1}\] Ta se točka ne može nalaziti između naboja Q1 i Q2 jer su orijentacije polja jednake, a također ni desno od naboja Q2 jer je u tom području iznos polja kojega stvara naboj Q2 veći od iznosa polja kojega stvara naboj Q1, \(E_{2} > E_{1}\). Prema tome, tražena točka nalazi se lijevo od naboja Q1 i na crtežu je označena slovom T. Za tu točku vrijedi: \[k\frac{Q_{1}}{r_{1}^{2}}=k\frac{Q_{2}}{r_{2}^{2}}\] Sredimo ovu jednadžbu: \[\frac{r_{2}^{2}}{r_{1}^{2}}=\frac{Q_{2}}{Q_{1}}\] Iz crteža zaključujemo da je \(r_{2}=r_{1}+d\) pa prethodnu jednadžbu možemo prikazati kao: \[\left(\frac{r_{1}+d}{r_{1}}\right)^{2}=\frac{Q_{2}}{Q_{1}}\] Odredimo \(r_{1}\): \[\frac{r_{1}+d}{r_{1}}=\sqrt {2}\] \[r_{1}\left(\sqrt {2}-1\right)=d\] \[r_{1}=108,64\,\textrm{cm}\]
34. zadatak
Kamen mase
Koliki je rad potreban za svladavanje otpora zraka ako kamen udari o podlogu brzinom
Odgovor: J
Pomoć potražite na poveznici Očuvanje mehaničke energije.
U početnom položaju mehanička energija kamena jednaka je zbroju njegove gravitacijske potencijalne energije i kinetičke energije: \[E_{1}=m\,g\,h+\frac{m\,v_{0}^{2}}{2}\] U trenutku kada kamen padne na podlogu gravitacijska potencijalna energija jednaka je nuli pa je mehanička energija jednaka \[E_{2}=\frac{m\,v^{2}}{2}\] Dio početne mehaničke energije pretvori se u konačnu mehaničku energiju, a dio u rad potreban za svladavanje otpora zraka: \[E_{1}=E_{2}+W\] Odredimo traženi rad: \[W=E_{1}-E_{2}\] \[W=m\,g\,h+\frac{m\,v_{0}^{2}}{2}-\frac{m\,v^{2}}{2}=4250\,\textrm{J}\]
35. zadatak
Strujni krug na slici sastoji se od baterije napona 12 V, tri žaruljice svaka otpora 2 Ω i sklopke.
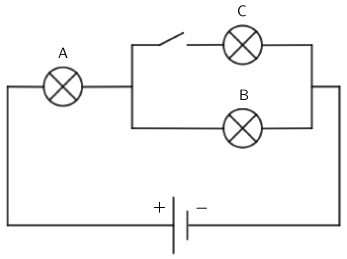
Odgovor: W
Pomoć potražite na poveznici Električna snaga.
Odredimo ukupni otpor kruga nakon što zatvorimo sklopku. Otpor paralelno spojenih žaruljica B i C jednak je: \[\frac{1}{R_{\textrm{BC}}}=\frac{1}{R_\textrm{B}}+\frac{1}{R_\textrm{C}}=\frac{1}{2}+\frac{1}{2}=1\,\Omega^{-1}\] \[R_{\textrm{BC}}=1\,\Omega\] Ukupni otpor kruga jednak je: \[R=R_{\textrm{A}}+R_{\textrm{BC}}=3\,\Omega\] Struju kroz žaruljicu A odredimo iz Ohmovog zakona za cijeli strujni krug: \[I=\frac{U}{R}=\frac{12}{3}=4\,\textrm{A}\] Snaga na žaruljici A jednaka je: \[P=U\,I=I\,R_{\textrm{A}}\,I=I^{2}\,R_{\textrm{A}}=32\,\textrm{W}\]
36. zadatak
Djevojčica i dječak stoje na obali rijeke i odmaraju se slušajući cvrkut ptice. Djevojčica koja se nalazi na udaljenosti 75 cm
od ptice mjeri zvuk intenziteta \(2,1\cdot 10^{-8}\, \textrm{W}/\textrm{m}^{2}\).
Koliki intenzitet zvuka mjeri dječak koji se nalazi na udaljenosti 3,75 m od ptice?
Kolika je snaga zvučnih valova nastalih cvrkutom ptice?
Intenzitet: \(\textrm{W}/\textrm{m}^{2}\)
Snaga: W
Pomoć potražite na poveznici Intenzitet valova zvuka.
Energija \(E\) zvučnih valova koja prolazi kroz jediničnu površinu u jedinici vremena okomito na smjer širenja energije zvučnog vala zove se jakost ili intenzitet zvuka. \[I=\frac{E}{S\,t}\] Točkasti izvor zvuka emitira zvuk jednako u svim smjerovima. Ti valovi prolaze kroz zamišljenu sferu polumjera \(r\) kojoj je središte u izvoru zvuka. Kod sfernih valova koje emitira točkasti izvor energija prolazi kroz sferu površine \(S=4\,r^{2}\,\pi\). Uvrstimo tu površinu u izraz za intenzitet zvuka: \[I=\frac{E}{4\,r^{2}\,\pi\,t}\] Intenzitet zvuka kojega mjeri djevojčica: \[I_{1}=\frac{E}{4\,r_{1}^{2}\,\pi\,t}\] Intenzitet zvuka kojega mjeri dječak: \[I_{2}=\frac{E}{4\,r_{2}^{2}\,\pi\,t}\] Podijelimo drugu jednadžbu prvom: \[\frac{I_{2}}{I_{1}}=\frac{E}{4\,r_{2}^{2}\,\pi\,t}\cdot\frac{4\,r_{1}^{2}\,\pi\,t}{E}=\left(\frac{r_{1}}{r_{2}}\right)^{2}\] Intenzitet zvuka kojega mjeri dječak: \[I_{2}=I_{1}\left(\frac{r_{1}}{r_{2}}\right)^{2}\] \[I_{2}=2,1\cdot 10^{-8}\cdot 0,04=8,4\cdot 10^{-10}\,\textrm{W}/\textrm{m}^{2}\] Snaga zvučnih valova nastalih cvrkutom ptica na mjestu gdje se nalazi dječak: \[P=I_{2}\,S=1,48\cdot 10^{-7}\,\textrm{W}\]
37. zadatak
Jednakokračni pravokutni trokut katete \(\sqrt {3}\,\textrm{cm}\) miruje u nekome inercijskom sustavu. Promatrač se giba paralelno s jednom njegovom
katetom brzinom \(c/2\).
Koliku površinu trokuta mjeri promatrač?
Odgovor: \(\textrm{cm}^{2}\)
Pomoć potražite na poveznici Kontrakcija duljine.
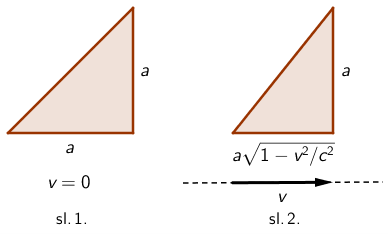
Promatrač koji u odnosu na trokut miruje mjerenjem dobije da su obje katete jednake (sl. 1.). Površina trokuta za njega je jednaka: \[P_{0}=\frac{1}{2}\,a^{2}=1,5\,\textrm{cm}^{2}\] Promatrač koji se u odnosu na trokut giba jednolikom brzinom u smjeru horizontalne katete mjerenjem dobije da je ta kateta kraća (sl. 2.) zbog kontrakcije duljine. Vertikalna kateta je okomita na smjer gibanja pa se njezina duljina ne mijenja. Površina trokuta za tog je promatrača jednaka: \[P=\frac{1}{2}\,a^{2}\,\sqrt{1-v^{2}/c^{2}}=1,3\,\textrm{cm}^2\]