Ljetni rok 2010. godine
1. zadatak
Slika prikazuje graf ubrzanja nekoga tijela u ovisnosti o vremenu. Tijelo se giba duž \(x\)-osi. U trenutku \(t=0\,\textrm{s}\) tijelo miruje, tj. \(v_{0}=0\,\textrm{m}/\textrm{s}\)
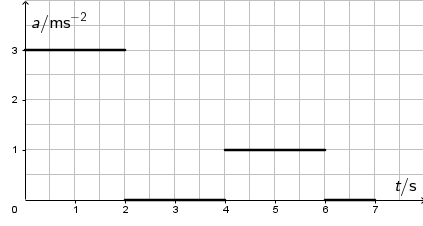
Koja slika prikazuje graf brzine toga tijela u ovisnosti o vremenu?
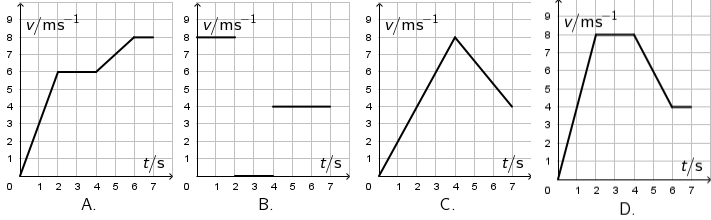
- A. Graf A.
- B. Graf B.
- C. Graf C.
- D. Graf D.
Kako iz \(a,t\) grafa određujemo brzinu tijela?
Iz \(a,t\) grafa zaključujemo:
- U prve dvije sekunde gibanje je jednoliko ubrzano: \(a=3\,\textrm{m}/\textrm{s}^{2}\)\)
- U trećoj i četvrtoj sekundi gibanje je jednoliko: \(a=0\,\textrm{m}/\textrm{s}^{2}\)
- U petoj i šestoj sekundi gibanje je jednoliko ubrzano: \(a=1\,\textrm{m}/\textrm{s}^{2}\)
- U sedmoj sekundi gibanje je jednoliko: \(a=0\,\textrm{m}/\textrm{s}^{2}\)
2. zadatak
Polumjer Zemljine putanje oko Sunca je 390 puta veći od polumjera Mjesečeve putanje oko Zemlje. Mjesec obiđe Zemlju približno 13 puta u godini dana.
Koliki je omjer brzine kruženja Zemlje oko Sunca \(v_{\small{\textrm{Z}}}\) i brzine kruženja Mjeseca oko Zemlje \(v_{\small{\textrm{M}}}\)?
- A. \(v_{\small{\textrm{Z}}}:v_{\small{\textrm{M}}}=1:13\)
- B. \(v_{\small{\textrm{Z}}}:v_{\small{\textrm{M}}}=13:1\)
- C. \(v_{\small{\textrm{Z}}}:v_{\small{\textrm{M}}}=1:30\)
- D. \(v_{\small{\textrm{Z}}}:v_{\small{\textrm{M}}}=30:1\)
Pomoć potražite na poveznici Jednoliko kružno gibanje.
\[\frac{v_{\small{\textrm{Z}}}}{v_{\small{\textrm{M}}}}=\frac{2\,r_{\small{\textrm{Z}}}\pi}{T_{Z}}\cdot\frac{T_{M}}{2\,r_{\small{\textrm{M}}}\,\pi} =\frac{r_{\small{\textrm{Z}}}}{r_{\small{\textrm{M}}}}\cdot\frac{T_{M}}{T_{Z}}\] \[\frac{v_{\small{\textrm{Z}}}}{v_{\small{\textrm{M}}}}=\frac{390\,r_{\small{\textrm{M}}}}{r_{\small{\textrm{M}}}}\cdot\frac{1}{13}=30\]
3. zadatak
Kugla mase 0,2 kg udari u mirnu kuglu mase 0,5 kg
brzinom 4 m/s.
Koliko iznosi ukupna količina gibanja tih dviju kugli nakon sudara?
- A. 0,8 kg m/s
- B. 1,2 kg m/s
- C. 2,0 kg m/s
- D. 2,8 kg m/s
Primijenite zakon očuvanja količine gibanja.
Ukupna količina gibanja prije sudara \(m_{1}\,v_{1}+m_{2}\,v_{2}=0,2\cdot 4+0=0,8\,\textrm{kg}\,\textrm{m}/\textrm{s}\) jednaka je ukupnoj količini gibanja nakon sudara. Točan odgovor je A.
4. zadatak
Tijelo K gustoće \(\rho_{\small{\textrm{K}}}\) i tijelo L gustoće \(\rho_{\small{\textrm{L}}}\) drže se uronjeni ispod površine vode gustoće \(\rho.\)
Kada se tijela ispuste, tijelo K ispliva, a tijelo L ostane u istome položaju.
Koji odnos vrijedi za gustoće tijela i vode?
- A. \(\rho_{\small{\textrm{K}}} < \rho < \rho_{\small{\textrm{L}}}\)
- B. \(\rho_{\small{\textrm{K}}} < \rho = \rho_{\small{\textrm{L}}}\)
- C. \(\rho_{\small{\textrm{K}}} < \rho_{\small{\textrm{L}}} < \rho\)
- D. \(\rho_{\small{\textrm{K}}} = \rho < \rho_{\small{\textrm{L}}}\)
Tijelo gustoće \(\rho_{\textrm{tijelo}}\) uronjeno u fluid gustoće \(\rho\) će:
- tonuti, ako je \(\rho_{\textrm{tijelo}} > \rho\)
- lebdjeti, ako je \(\rho_{\textrm{tijelo}} = \rho\)
- izranjati, ako je \(\rho_{\textrm{tijelo}} < \rho\)
Tijelo K ispliva, a to znači da je \(\rho_{\small{\textrm{K}}} < \rho\).
Tijelo L lebdi, a to znači da je \(\rho_{\small{\textrm{L}}} = \rho\)
5. zadatak
Na termometru je očitana temperatura zraka od 290 K.
Kolika je temperatura zraka u Celzijevim stupnjevima?
- A. \(15\,^{0}\textrm{C}\)
- B. \(17\,^{0}\textrm{C}\)
- C. \(19\,^{0}\textrm{C}\)
- D. \(21\,^{0}\textrm{C}\)
\[t/^{0}\textrm{C}=T/\textrm{K}-273,15\]
290 K - 273 = 17 0C Točan odgovor je B.
6. zadatak
Koja od navedenih tvrdnji ne vrijedi za model idealnoga plina?
- A. Kinetička energija nasumičnoga gibanja čestica plina manja je od potencijalne energije njihova međusobnoga djelovanja.
- B. Čestice plina se stalno nasumično gibaju.
- C. Sudari čestica plina sa stijenkama posude su savršeno elastični.
- D. Temperatura plina proporcionalna je srednjoj kinetičkoj energiji nasumičnoga gibanja čestica plina.
Model idealnog plina:
- Molekule zamišljamo kao malene kuglice.
- Gibanje molekula je nasumično (kaotično).
- Međusobni sudari molekula i sudari molekula sa stijenkama posude su elastični.
- Potencijalnu energiju molekula zanemarujemo jer molekule međusobno djeluju samo u trenucima sudara. Promjer molekule puno je manji od udaljenosti između njih pa su sudari rijetki.
U modelu idealnog plina zanemarujemo potencijalnu energiju molekula.
Točan odgovor je A.
7. zadatak
Temperatura idealnoga plina je 0 0C.
Na kojoj će temperaturi tlak plina biti dva puta veći od tlaka plina pri 0 0C ako se obujam plina
drži stalnim?
- A.
0 K - B.
137 K - C.
273 K - D.
546 K
Izohorna promjena stanja plina: \[\frac{p}{T}=\textrm{konst.}\]
Za izohornu promjenu stanja plina vrijedi:
\[\frac{p}{T}=\textrm{konst.}\]
Ako se tlak plina poveća dva puta, mora se i apsolutna temperatura povećati dva puta.
Početna temperatura je
\[T_{1}=273\,\textrm{K}\]
Konačna temperatura dva puta je veća:
\[T_{2}=2\,T_{1}=2\cdot 273=546\,\textrm{K}\]
8. zadatak
Dvije jednake metalne kugle prikazane na slici vise na nitima od izolatora. Obje kugle su početno električki neutralne. Kugla M nabije se negativno nabojem od -6 nC i zatim se dotakne kuglom N.
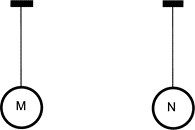
- A. -6 nC
- B. -3 nC
- C. 3 nC
- D. 6 nC
Primijenite zakon očuvanja električnog naboja.
Nakon dodirivanja kugle će imati jednak potencijal: \[\varphi=k\,\frac{q}{R^{2}}\] Kugle su jednake pa su im i polumjeri jednaki. Zbog jednakog potencijala zaključujemo da će im i naboji biti jednaki. Zbog očuvanja naboja ukupni je naboj -6 nC pa će naboj svake kugle biti -3 nC.
9. zadatak
U strujnome krugu prikazanome na slici ampermetar pokazuje 2 A. Unutrašnji otpor baterije je zanemariv.
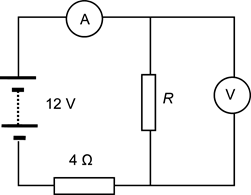
Koliki napon pokazuje voltmetar uz uvjet da su instrumenti idealni?
- A. 4 V
- B. 6 V
- C. 8 V
- D. 12 V
Zadatak se može riješiti primijenom Ohmovog zakona ili drugog Kirchhoffovog pravila.
Primijenimo drugo Kirchhoffovo pravilo: \[12=I\cdot 4+I\cdot R\] Za otpor se dobije \[R=2\,\Omega\] Voltmetar pokazuje \[U_{\small{\textrm{R}}}=I\cdot R=4\,\textrm{V}\]
10. zadatak
Vodičem teče struja od 0,5 mA.
Koliko elektrona prođe poprečnim presjekom vodiča za 0,1 s?
- A. 0,5·1014
- B. 3,125·1014
- C. 3,125·1017
- D. 3,125·1019
Iz poznate struje odredimo koliki naboj prođe poprečnim presjekom vodiča za vrijeme \(t\): \[q=I\,t\] Električni naboj je kvantiziran (sastoji se od cijelog broja elektrona): \[q=N\,e\]
\[N=\frac{q}{e}=\frac{I\,t}{e}=3,125\cdot 10^{14}\]
11. zadatak
Na slici su prikazane silnice električnoga polja.
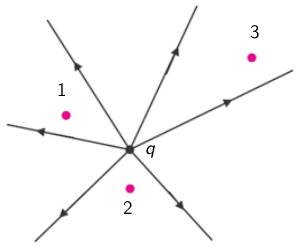
Koji odnos vrijedi za iznose električnoga polja u označenim točkama 1, 2 i 3?
- A. \(E_{3} > E_{2} > E_{1}\)
- B. \(E_{2} > E_{1} > E_{3}\)
- C. \(E_{1} > E_{3} > E_{2}\)
- D. \(E_{3} > E_{1} > E_{2}\)
Električno polje u točki koja je za \(r\) udaljena od naboja \(q\) obrnuto je proporcionalno kvadratu udaljenosti: \[E=k\,\frac{q}{r^{2}}\]
Točka 2 najbliža je naboju pa je polje \(E_{2}\) najveće, dok je točka 3 najudaljenija od naboja pa je polje najmanje.
12. zadatak
Na udaljenosti 2 m od ravnoga vodiča kojim teče stalna struja magnetsko polje iznosi 4 mT.
Koliko će iznositi magnetsko polje na udaljenosti 1 m od toga vodiča?
- A. 2 mT
- B. 4 mT
- C. 8 mT
- D. 16 mT
Magnetsko polje oko dugog ravnog vodiča na jednakim udaljenostima od vodiča ima jednak iznos. To znači da su magnetske silnice kružnice sa središtem na vodiču.
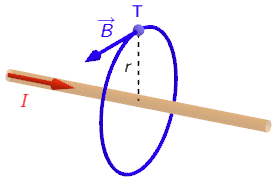
Smjer magnetskog polja u nekoj točki silnice jednak je tangentni na silnicu u toj točki. Orijentaciju magnetskog polja odredimo pravilom desne ruke. Iznos magnetskog polja ovisi o struji \(I\) kroz vodič i o udaljenosti \(r\) od vodiča: \[B=\frac{\mu_{0}\,\mu_{r}}{2\,\pi}\,\frac{I}{r}\]
Konstantu \(\mu_{0}\) nazivamo permeabilnost vakuuma. Njezina je vrijednost: \[\mu_{0}=4\,\pi \cdot 10^{-7}\,\frac{\textrm{T}\,\textrm{m}}{\textrm{A}}\]
Konstantu \(\mu_{r}\) nazivamo permeabilnost sredstva . Njezina vrijednost ovisi o sredstvu u kojemu se vodič nalazi.
\[B=\frac{\mu_{0}\,\mu_{r}}{2\,\pi}\,\frac{I}{r}\] Magnetsko polje u nekoj točki obrnuto je proporcionalno udaljenosti od vodiča. Na dva puta manjoj udaljenosti imat će dva puta veći iznos: \[B=8\,\textrm{T}\]
13. zadatak
Konvergentna leća ima žarišnu daljinu \(f\).
Kakva slika nastane kada je udaljenost predmeta od leće manja od \(f\) ?
- A. realna i uvećana
- B. realna i umanjena
- C. virtualna i uvećana
- D. virtualna i umanjena
Pomoć potražite na poveznici Jednadžba leće.
Ako se predmet nalazi između žarišta i tjemena konvergentne leće slika je uspravna, uvećana i virtualna.
14. zadatak
Na optičku rešetku okomito upada monokromatska svjetlost valne duljine 400 nm.
Sinus ogibnoga kuta za prvi maksimum iznosi 0,2.
Kolika je konstanta optičke rešetke?
- A. 1 μm
- B. 2 μm
- C. 3 μm
- D. 4 μm
Ogibom svjetlosti na optičkoj rešetki nastaju svjetle pruge ako je: \[d\,\textrm{sin}\,\alpha_{\textrm{k}}=k\,\lambda\] Redni broj svjetlih pruga određen je vrijednošću broja \(k\): \[k=1,\,2,\,3,\,...\]
\[d\,\textrm{sin}\,\alpha_{\textrm{k}}=k\,\lambda\] \[d=\frac{k\,\lambda}{\textrm{sin}\,\alpha_{\textrm{k}}}=2\cdot 10^{-6}\,\textrm{m}=2\,\mu\textrm{m}\]
15. zadatak
Na grafu je prikazano kako elongacija tijela koje titra ovisi o vremenu.
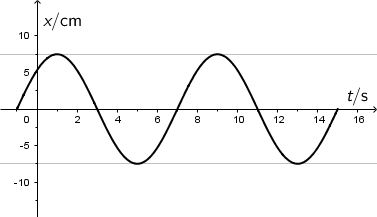
Kolika je amplituda titranja tijela?
- A. 4,5 cm
- B. 5,0 cm
- C. 7,5 cm
- D. 8,0 cm
Amplituda titranja jednaka je najvećoj elongaciji (apsolutna vrijednost najveće udaljenosti od ravnotežnog položaja).
Iz grafa očitavamo da je amplituda: \[A=7,5\,\textrm{cm}\]
16. zadatak
Val prelazi iz sredstva A u sredstvo B. U sredstvu A brzina vala iznosi 100 m/s,
a valna duljina 0,5 m. U sredstvu B valna se duljina poveća na 0,8 m.
Kolika je brzina vala u sredstvu B?
- A. 50 m/s
- B. 80 m/s
- C. 100 m/s
- D. 160 m/s
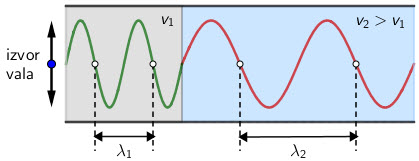
Brzina vala ovisi o svojstvima sredstva kroz koje se val širi.
Kada val prelazi iz jednog sredstva u drugo, mijenja se njegova brzina pa prema tome i valna duljina.
\[\lambda=\frac {v}{f}\]
Frekvencija vala, koja je jednaka frekvenciji titranja izvora, ne mijenja se.
\[v=f\,\lambda\] \[f=\frac{v_{\small{\textrm{A}}}}{\lambda_{\small{\textrm{A}}}}=\frac{100}{0,5}=200\,\textrm{Hz}\] \[v_{\small{\textrm{B}}}=f\,\lambda_{\small{\textrm{B}}}=200\cdot 0,8=160\,\textrm{m}/\textrm{s}\]
17. zadatak
Slika prikazuje harmonijski oscilator sastavljen od utega pričvršćenoga za oprugu koji neprigušeno harmonijski titra. Ukupna energija toga oscilatora iznosi 6 J.

Kolika je kinetička energija utega u trenutku kad on prolazi kroz ravnotežni položaj?
- A. 0 J
- B. 3 J
- C. 4 J
- D. 6 J
Primijenite zakon očuvanja energije. Ukupna energija jednaka je: \[E=E_{\textrm{p,e}}+E_{\textrm{k}}=6\,\textrm{J}\]
U ravnotežnom položaju elastična potencijalna energija jednaka je nuli. To znači da je kinetička energija: \[E_{\textrm{k}}=E-E_{\textrm{p,e}}=6-0=6\,\textrm{J}\]
18. zadatak
Elektron u atomu prelazi sa stanja više energije \(E_{2}\) u stanje niže energije \(E_{1}\).
Što se događa s atomom?
- A. emitira foton energije \(E_{2}-E_{1}\)
- B. absorbira foton energije \(E_{2}-E_{1}\)
- C. emitira foton energije \(E_{1}\)
- D. apsorbira foton energije \(E_{1}\)
Atomi ne mogu poprimiti bilo koju energiju, nego samo neke, točno određene vrijednosti energije. Te energije zovemo energijske razine. O vrsti atoma ovise vrijednosti tih dopuštenih energija. Stanje u kojemu se nalazi atom kada mu je energija najmanja zove se osnovno stanje. Sva druga stanja su pobuđena stanja.
Skup svih dopuštenih energijskih stanja nekog atoma zovemo energijski spektar. Energijski spektar atoma je kvantiziran. To znači da atom ne može poprimiti bilo koju vrijednost energije, nego samo točno određene vrijednosti energije.
Ako se atom nađe u nekom pobuđenom stanju, prelazit će spontano u niža energijska stanja sve dok ne dođe do osnovnog stanja. Pritom atom emitira fotone elektromagnetskog zračenja kojima je energija jednaka razlici energija početnog i konačnog stanja: \[E_{\textrm{f}}=E_{\textrm{poč}}-E_{\textrm{kon}}\] Ovaj proces nazivamo emisija zračenja.
Kada atom prelazi iz stanja više energije \(E_{2}\) u stanje niže energije \(E_{1}\) dolazi do emisije fotona energije: \[E_{\textrm{f}}=E_{2}-E_{1}\]
19. zadatak
Što atomska jezgra emitira pri \(\beta^{-}\) raspadu?
- A. proton
- B. neutron
- C. pozitron
- D. elektron
- Alfa-zračenjem dolazi do emisije alfa-čestice (jezgra atoma helija): \[_{Z}^{A}\textrm{X}\rightarrow _{2}^{4}\textrm{He}+\,_{Z-2}^{A-4}\textrm{Y}\]
- Beta-minus zračenjem dolazi do emisije brzih elektrona: \[_{Z}^{A}\textrm{X}\rightarrow _{-1}^{\;\;0}\textrm{e}+\,_{Z+1}^{\;\;\;A}\textrm{Y}\] Beta-plus zračenjem dolazi do emisije pozitrona: \[_{Z}^{A}\textrm{X}\rightarrow _{+1}^{\;\;0}\textrm{e}+\,_{Z-1}^{\;\;\;A}\textrm{Y}\] Gama-zračenjem dolazi do emisije elektromagnetskih valova \(\left(\gamma \textrm{fotona}\right)\): \[_{Z}^{A}\,\textrm{X}^{*}\rightarrow \gamma+\,_{Z}^{A}\textrm{X}\]
Beta-minus radioaktivnim raspadom \[_{Z}^{A}\textrm{X}\rightarrow _{-1}^{\;\;0}\textrm{e}+\,_{Z+1}^{\;\;\;A}\textrm{Y}\] dolazi do emisije elektrona.
20. zadatak
Za koje je vrijednosti A i Z moguća nuklearna reakcija:
\[{_{\,7}^{A}}\,\textrm{X}+{_{2}^{4}}\,\textrm{He}\rightarrow{_{\,Z}^{17}}\,\textrm{Y}+{_{1}^{1}}\,\textrm{X}\]
- A. \(A = 10, Z = 5\)
- B. \(A = 12, Z = 8\)
- C. \(A = 14, Z = 4\)
- D. \(A = 14, Z = 8\)
U nuklearnim reakcijama vrijede sljedeći zakoni očuvanja:
-
Očuvanje električnog naboja: \(Z_{1}+Z_{2}=Z_{3}+Z_{4}\).
Broj protona prije reakcije \(Z_{1}+Z_{2}\), jednak je broju protona nakon reakcije \(Z_{3}+Z_{4}\). -
Očuvanje broja nukleona: \(A_{1}+A_{2}=A_{3}+A_{4}\).
Broj nukleona prije reakcije \(A_{1}+A_{2}\), jednak je broju nukleona nakon reakcije \(A_{3}+A_{4}\). -
Očuvanje ukupne relativističke energije: \(E_{1}+E_{2}=E_{3}+E_{4}\).
Ukupna energija prije reakcije \(E_{1}+E_{2}\), jednaka je ukupnoj energiji nakon reakcije \(E_{3}+E_{4}\). -
Očuvanje količine gibanja: \(p_{1}+p_{2}=p_{3}+p_{4}\).
Ukupna količina gibanja prije reakcije \(p_{1}+p_{2}\), jednaka je ukupnoj količini gibanja nakon reakcije \(p_{3}+p_{4}\).
Za rješenje zadatka primijenite prva dva zakona očuvanja.
Primjenom zakona očuvanja broja protona u jezgri zaključujemo da je: \[Z=8\] Primjenom zakona očuvanja broja nukleona u jezgri zaključujemo da je: \[A=14\]
21. zadatak
Foton energije 3,27 eV izazove fotoelektrični učinak na nekome metalu.
Izlazni rad fotoelektrona za taj metal je 2,08 eV.
Kolika je kinetička energija fotoelektrona?
- A. 1,19 eV
- B. 2,08 eV
- C. 3,27 eV
- D. 5,35 eV
Einsteinova jednadžba kojom je objasnio fotoelektrični učinak: \[E_{\textrm{f}}=W_{0}+E_{\textrm{k}}\]
- \(E_{\textrm{f}}\) - energija fotona koji padaju na metal
- \(W_{0}\) - izlazni rad metala
- \(E_{\textrm{k}}\) - maksimalna kinetička energija izbačenih elektrona (fotoelektroni)
Iz Einsteinove jednadžbe fotoelektričnog učinka \[E_{\textrm{f}}=W_{0}+E_{\textrm{k}}\] odredimo maksimalnu kinetičku energiju fotoelektrona: \[E_{\textrm{k}}=E_{\textrm{f}}-W_{0}=1,19\,\textrm{eV}\]
22. zadatak
Jabuka pada na Zemlju zbog gravitacijskoga privlačenja između nje i Zemlje.
Označi li se sila kojom Zemlja privlači jabuku s \(F_{1}\), a sila kojom jabuka privlači Zemlju s \(F_{2}\), u kakvome su odnosu iznosi tih dviju sila?
- A. \(F_{1} < F_{2}\)
- B. \(F_{1} = F_{2}\)
- C. \(F_{1} > F_{2}\)
Treći Newtonov zakon (zakon akcije i reakcije):
Sile kojima međusobno djeluju dva tijela imaju jednak iznos i smjer, ali suprotnu orijentaciju:
\[\vec{F}_{1}=-\vec{F}_{2}\]
Primjenom trećeg Newtonovog zakona zaključujemo da su iznosi sila jednaki: \[F_{1} = F_{2}\]
23. zadatak
Tijelo A slobodno pada s visine \(h\), a tijelo B je s iste visine \(h\) izbačeno u vodoravnome smjeru.
Kako se odnose vrijeme gibanja tijela A \(t_{\small{\textrm{A}}}\) i vrijeme gibanja tijela B \(t_{\small{\textrm{B}}}\) do trenutka pada?
- A. \(t_{\small{\textrm{A}}} < t_{\small{\textrm{A}}}\)
- B. \(t_{\small{\textrm{A}}} = t_{\small{\textrm{A}}}\)
- C. \(t_{\small{\textrm{A}}} > t_{\small{\textrm{A}}}\)
Tijelo koje slobodno pada s visine \(h\) past će na tlo nakon vremena:
\[t=\sqrt{\frac{2\,h}{g}}\]
Tijelo koje je s iste visine izbačeno u vodoravnom smjeru izvodi složeno gibanje.
To se gibanje sastoji od:
- jednolikog gibanja po vodoravnom pravcu brzinom kojom je izbačeno
- i slobodnog pada u vertikalnom smjeru
\[t_{\small{\textrm{A}}}=t_{\small{\textrm{B}}}=\sqrt{\frac{2\,h}{g}}\]
24. zadatak
De Broglieve valne duljine elektrona i protona bit će jednake kada elektron i proton imaju jednake:
- A. količine gibanja
- B. kinetičke energije
- C. brzine
De Broglieva valna duljina čestice mase \(m\) koja se giba brzinom \(v\): \[\lambda=\frac{h}{m\,v}\] U nazivniku je količina gibanja čestice: \[p=m\,v\] Zato de Broglievu valnu duljinu možemo prikazati i kao: \[\lambda=\frac{h}{p}\]
De Broglieva valna duljina: \[\lambda=\frac{h}{p}\] Elektron i proton će imati jednaku de Broglievu valnu duljinu ako su im jednake količine gibanja.
25. zadatak
Tijelo mase 10 kg pada s visine 80 m i pri udarcu o površinu Zemlje ima
kinetičku energiju 4500 J.
Koliko je energije tijelo utrošilo na savladavanje otpora zraka?
Odgovor: J
Primijenite zakon očuvanja mehaničke energije.
Gravitacijska potencijalna energija pretvara se u rad na savladavanju otpora zraka i u kinetičku energiju: \[m\,g\,h=W+E_{\textrm{k}}\] Rad (energija) potreban za savladavanje otpora zraka je: \[W=m\,g\,h-E_{\textrm{k}}=3500\,\textrm{J}\]
26. zadatak
Kolikom silom Mars privlači kamen mase 1 kg koji se nalazi na njegovoj površini?
Masa Marsa je 6,5·1023 kg, a polumjer 3400 km.
Odgovor: N
Primijenite Newtonov zakon gravitacije.
Udaljenost između središta tijela mase \(M\) i tijela mase \(m\) je \(r\). Ta se dva tijela međusobno privlače gravitacijskom silom: \[F=G\,\frac{M\,m}{r^{2}}\] Udaljenost između tijela jednaka je polumjeru Marsa \(R\): \[F=G\,\frac{M\,m}{R^{2}}=3,75\,\textrm{N}\]
27. zadatak
Pri stalnome tlaku od 105 Pa plin obavi rad od 1000 J.
Za koliko se povećao obujam plina?
Odgovor: \(\textrm{m}^{3}\)
Rad plina pri stalnom tlaku: \[W=p\,\Delta V\]
Povećanje volumena plina je: \[\Delta V=\frac{W}{p}=0,01\,\textrm{m}^{3}\]
28. zadatak
Krug izmjenične struje sastavljen je od zavojnice zanemarivoga omskoga otpora i induktivnoga otpora 600 Ω
te kondenzatora kapacitivnoga otpora 200 Ω.
Koliko iznosi impedancija ovoga strujnoga kruga?
Odgovor: \(\Omega\)
Ukupan otpor u krugu izmjenične struje (impedancija) u kojemu su serijski spojeni zavojnica, kondenzator i otpornik: \[Z=\sqrt{R^{2}+\left(R_{\small{\textrm{L}}}-R_{\small{\textrm{C}}}\right)^{2}}\]
Omski otpor je zanemariv pa je impedancija jednaka: \[Z=\sqrt{\left(R_{\small{\textrm{L}}}-R_{\small{\textrm{C}}}\right)^{2}}=400\,\Omega\]
29. zadatak
U radioprijamniku se ugađanje frekvencije prijama ostvaruje pomoću LC kruga u kojem su serijski spojeni zavojnica induktiviteta
0,8 μH i kondenzator promjenljivoga kapaciteta.
Uz koju će se vrijednost kapaciteta moći primati program stanice koja emitira na 95 MHz?
Odgovor: pF
Period LC kruga odredimo pomoću frekvencije: \[T=\frac{1}{f}\] Period LC kruga ovisi o induktivitetu zavojnice \(L\) i kapacitetu kondenzatora \(C\): \[T=2\,\pi\,\sqrt{L\,C}\] To je Thomsonova formula koju možete pronaći u knjižici s formulama.
\[\frac{1}{f}=2\,\pi\,\sqrt{L\,C}\] Kapacitet kondenzatora je: \[C=\frac{1}{4\,\pi^{2}\,f^{2}L}=3,5\cdot 10^{-12}\,\textrm{F}=3,5\,\textrm{pF}\]
30. zadatak
Vlastito vrijeme života neke čestice iznosi \(T_{0}\).
Kolika treba biti brzina čestice u laboratorijskome sustavu da za promatrača u tome sustavu njezino vrijeme života iznosi \(2\,T_{0}\)?
Odgovor: m/s
Dilatacija vremena: \[T=\frac{T_{0}}{\sqrt{1-v^{2}/c^{2}}}\]
- \(T\)-vrijeme života čestice u laboratorijskom sustavu
- \(T_{0}\)-vlastito vrijeme života čestice
\[T=\frac{T_{0}}{\sqrt{1-v^{2}/c^{2}}}\] \[T=2\,T_{0}\] \[2\,T_{0}=\frac{T_{0}}{\sqrt{1-v^{2}/c^{2}}}\] \[\sqrt{1-v^{2}/c^{2}}=\frac{1}{2}\] \[v=\frac{\sqrt{3}}{2}=2,6\cdot 10^{8}\,\textrm{m}/\textrm{s}\]
31. zadatak
Sustav prikazan na slici sastoji se od jednoga koloturnika zanemarive mase i dvaju tijela. Trenje niti s koloturnikom može se zanemariti.
Tijela se gibaju akceleracijom od 1 ms-2. Sila trenja između stola i tijela mase
m2 iznosi 5 N.
Koliko iznosi masa m1?
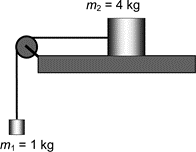
Odgovor: kg
Odredite rezultantu svih sila koje na tijelo mase \(m_{1}\) i primijenite drugi Newtonov zakon.
Odredite rezultantu svih sila koje na tijelo mase \(m_{2}\) i primijenite drugi Newtonov zakon.
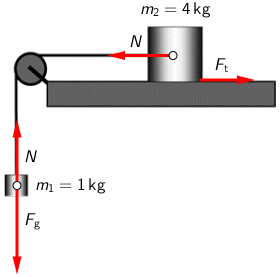
Na tijelo mase \(m_{1}\) djeluju sila teža vertikalno prema dolje i napetost niti vertikalno prema gore. Jednadžba gibanja toga tijela je: \[m_{1}\,g-N=m_{1}\,a\] Na tijelo mase \(m_{2}\) djeluju napetost niti prema lijevo i sila trenja prema desno. Jednadžba gibanja tog tijela je: \[N-F_{\textrm{t}}=m_{2}\,a\] Ove dvije jednadžbe zbrojimo: \[m_{1}\,g-F_{\textrm{t}}=m_{1}\,a+m_{2}\,a\] Iz posljednje jednadžbe odredimo \(m_{1}\): \[m_{1}=\frac{F_{\textrm{t}}+m_{2}\,a}{g-a}=1\,\textrm{kg}\]
32. zadatak
Voda se zagrijava u aluminijskome loncu uz stalno miješanje. Početno su voda i lonac na temperaturi od
20 0C. Nakon što zajedno prime 175,2 kJ topline, temperatura vode
i lonca poveća se na 60 0C.
Ako je masa vode 1 kg, masa lonca 0,2 kg, a specifični toplinski kapacitet vode
4200 J/(kg K), koliki je specifični toplinski kapacitet aluminija?
Odgovor: \(\large{\frac{\textrm{J}}{\textrm{kg}\,\textrm{K}}}\)
Toplina potrebna za zagrijavanje tijela: \[Q=m\,c\,\Delta t\]
- \(m\)-masa tijela
- \(c\)-specifični toplinski kapacitet tijela
- \(\Delta t\)-porast temperature tijela tijela
- \(r\)-specifična toplina isparavanja
- \(\lambda\)-specifična toplina taljenja
Primljena toplina pretvara se u toplinu zagrijavanja vode i aluminija: \[Q=m_{\textrm{v}}\,c_{\textrm{v}}\,\Delta t+m_{\small{\textrm{A}}}\,c_{\small{\textrm{A}}}\,\Delta t\] \[\Delta t=60–20=40\,^{0}\textrm{C}\] Specifični toplinski kapacitet aluminija je: \[c_{\small{\textrm{A}}}=\frac{Q-m_{\textrm{v}}\,c_{\textrm{v}}\,\Delta t}{m_{\small{\textrm{A}}}\,\Delta t}\] \[c_{\small{\textrm{A}}}=900\,\frac{\textrm{J}}{\textrm{kg}\,\textrm{K}}\]
33. zadatak
Na slici je prikazan bakreni štap duljine 80 cm cm koji leži u magnetskome polju iznosa 5 mT. Štap se jednoliko pomiče okomito na silnice polja brzinom 20 m/s.
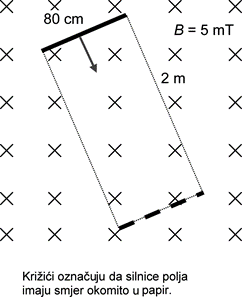
Koliki se napon inducira između krajeva štapa?
Na slici označite na kojem je kraju štapa + pol, a na kojem – pol.
Odgovor: V
Inducirani napon u vodiču duljine \(\ell\), koji se u magnetskom polju \(B\) giba brzinom \(v\) pri čemu smjer brzine i smjer magnetskog polja zatvaraju kut \(\alpha\): \[U_{\textrm{i}}=B\,\ell\,v\,\textrm{sin}\,\alpha\] Ako je kut \(\alpha=90\,^{0}\): \[U_{\textrm{i}}=B\,\ell\,v\]
\[U_{\textrm{i}}=B\,\ell\,v\] \[U_{\textrm{i}}=0,08\,\textrm{V}\] Primjenom pravila lijevog dlana zaključujemo da Lorentzova sila na elektrone djeluje prema lijevom kraju štapa pa će taj kraj biti negativno nabijen, a desni kraj štapa pozitivno nabijen.
34. zadatak
Učenici su četiri puta mjerili valnu duljinu svjetlosti pomoću interferencije svjetlosti na dvjema pukotinama i dobili sljedeće vrijednosti za isti izvor:
650 nm; 630 nm; 676 nm; 628 nm
Koji je rezultat njihova mjerenja zajedno s pripadnom maksimalnom apsolutnom pogrješkom?
\(\bar{\lambda}\) = nm
\(\left|\lambda\right|\) = nm
Srednja vrijednost
Srednja vrijednost jednaka je aritmetičkoj sredini kada smo izvršili nekoliko mjerenja neke fizičke veličine \(x\). Broj mjerenja označimo s \(n\):
\[\overline{x}=\frac{x_{1}+x_{2}+x_{3}\,+...+\,x_{n}}{n}\]
Maksimalna apsolutna pogreška
Odredimo odstupanja svakog pojedinog mjerenja od srednje vrijednosti:
\[\Delta x_{\textrm{i}}=x_{\textrm{i}}-\overline{x}\]
Iz ovako dobivenih odstupanja uzimamo ono koje je po apsolutnom iznosu najveće i to nazivamo maksimalnom apsolutnom pogreškom: \(\left|\Delta x\right|.\)
Zapis rezultata mjerenja
\[x=\left(\overline{x}\pm \left|\Delta x\right|\right)\,\left[\textrm{odgovarajuća jedinica}\right]\]
Obrada rezultata mjerenja.
- Srednja vrijednost \[\bar{\lambda}=\frac{\lambda_{1}+\lambda_{2}+\lambda_{3}+\lambda_{4}}{4}=646\,\textrm{nm}\]
- Maksimalna apsolutna pogreška \[\bar{\lambda}-\lambda_{\textrm{i}}:\,-4\,\textrm{nm};16\,\textrm{nm};-30\,\textrm{nm};18\,\textrm{nm}\] \[\left|\Delta\lambda\right|=30\,\textrm{nm}\]
- Zapis rezultata mjerenja \[\lambda=\left(646\pm30\right)\,\textrm{nm}\]
35. zadatak
Neko apsolutno crno tijelo zrači najviše energije na valnoj duljini od \(5,8\cdot 10^{-6}\,\textrm{m}.\)
Kolika je snaga zračenja toga tijela ako mu površina iznosi \(0,1\,\textrm{m}^{2}?\)
Odgovor: W
Stefan-Boltzmannov zakon: \[P=\sigma\,S\,T^{4}\] Wienov zakon: \[\lambda_{\textrm{maks}}\cdot T=b\]
Iz Stefan-Boltzmannovog i Wienovog zakona dobivamo: \[P=\sigma\,S\,\left(\frac{b}{\lambda_{\textrm{maks}}}\right)^{4}=350\,\textrm{W}\]