Ljetni rok 2024. godine
1. zadatak
Tijelo se giba stalnom brzinom duž osi x. Na tijelo počne djelovati stalna sila usmjerena duž osi y.
Koja je od navedenih tvrdnja za gibanje tijela točna?
- A. Iznos brzine tijela i smjer gibanja tijela neće se promijeniti.
- B. Iznos brzine tijela ostat će isti, a promijenit će se smjer gibanja tijela.
- C. Iznos brzine tijela će se smanjiti, a smjer gibanja tijela promijeniti.
- D. Iznos brzine tijela će se povećati, a smjer gibanja tijela promijeniti.
Ovo je primjer složenog gibanja, koje se sastoji od jednolikog gibanja u smjeru osi x i jednoliko ubrzanog gibanja u smjeru osi y.
Pokrenite video.
Tijelo se giba po paraboli. Smjer gibanja u bilo kojoj točki parabole jednak je smjeru tangente na parabolu u toj točki. Iz videa zaključujemo da se smjer gibanja
stalno mijenja.
Brzinu tijela odredimo vektorskim zbrajanjem brzina u smjeru osi x i osi y.
Tijelo se u smjeru osi x giba jednoliko po pravcu:
\[v_\textrm{x}=\frac{x}{t}\]
Zbog djelovanja sile, tijelo se u smjeru osi y giba jednoliko ubrzano:
\[v_\textrm{y}=a\,t\]
U videu vidimo da je brzina u smjeru osi x konstantna, dok se u smjeru osi y povećava.
Zbog toga se i rezultantna brzina \(v\) povećava.
Točan odgovor je D.
2. zadatak
Loptica mase m leti u vodoravnome smjeru brzinom v i udara okomito o vertikalni nepomični
zid. Sudar loptice sa zidom savršeno je elastičan.
Koliki je impuls sile kojim je zid djelovao na lopticu?
- A. \(\frac{1}{2}\,m\,v\)
- B. \(m\,v\)
- C. \(2\,m\,v\)
- D. \(4\,m\,v\)
Impuls sile jednak je umnošku sile i intervala vremena u kojemu je sila djelovala: \[F\,\Delta t\] Impuls sile kojim loptica djeluje na zid moguće je prikazati kao razliku količina gibanja loptice nakon i prije sudara sa zidom. \[F\,\Delta t=m\,v_2-m\,v_1\]
Pokrenite video.
Impuls sile kojim je loptica djelovala na zid: \[F\,\Delta t=-m\,v-\left(m\,v\right)=-2\,m\,v\] Prema trećem Newtonovom zakonu zid je djelovao na lopticu jednakom, ali suprotno orijentiranom silom pa je impuls sile kojim je zid djelovao na lopticu: \[-F\,\Delta t=-m\,v-\left(m\,v\right)=2\,m\,v\] Točan odgovor je C.
3. zadatak
Tijelo ovješeno na nit spušta se prema tlu tako da se giba jednoliko.
Koja je od navedenih tvrdnja o radu sile napetosti niti i radu gravitacijske sile na tijelo tijekom gibanja točna?
- A. Oba su rada pozitivna.
- B. Oba su rada jednaka nuli.
- C. Rad napetosti niti je pozitivan, a rad gravitacijske sile negativan.
- D. Rad napetosti niti je negativan, a rad gravitacijske sile pozitivan.
Ako tijelo ovjesimo na nit ili ga vučemo pomoću niti, na tijelo će djelovati sila koju nazivamo napetost niti. Znak za napetost niti je
FN
Hvatište napetosti niti je u tijelu kojega nit nateže, a orijentacija je prema točki u kojoj je nit ovješena.
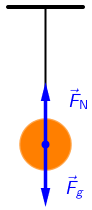
Tijelo se giba jednoliko (giba se stalnom brzinom), što znači da je ukupna sila koja djeluje na tijelo jednaka nuli (prema Newtonovom prvom zakonu gibanja).
Gravitacijska sila FG djeluje vertikalno prema dolje i uzrokuje da tijelo pada.
Sila napetosti niti FN djeluje prema gore i suprotstavlja se gravitacijskoj
sili. Rezultantna sila jednaka je nuli i gibanje je jednoliko.
Rad gravitacijske sile je pozitivan jer gravitacijska sila djeluje u smjeru gibanja tijela.
Rad sile napetosti niti je negativan jer djeluje u suprotnom smjeru od gibanja tijela.
Točan odgovor je D.
4. zadatak
Na kojoj je slici ispravno prikazana ukupna sila na meteorološki satelit S dok jednoliko kruži oko Zemlje Z?
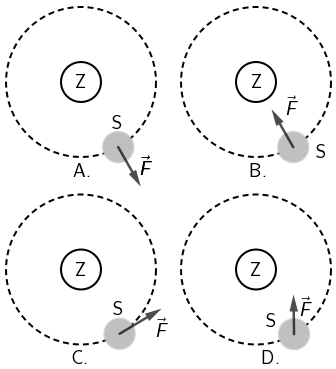
- A. Na slici A.
- B. Na slici B.
- C. Na slici C.
- D. Na slici D.
Satelit se giba jednoliko po kružnici kojoj je središte u središtu Zemlje, a to znači da na njega mora djelovati sila koja je u svakoj točki usmjerena prema središtu Zemlje.
Na satelit djeluje gravitacijska sila Zemlje koja je usmjerena prema njezinom središtu. Zato se satelit giba jednoliko po kružnici.
Točan odgovor je B.
5. zadatak
Horizontalna cijev kroz koju prolazi tekućina ima širi i uži dio. Statički i dinamički tlakovi
tekućine u širemu dijelu cijevi su pSA i
pDA, a u užemu dijelu cijevi su
pSB i
pDB.
Koja je od navedenih tvrdnja o odnosima tlakova u cijevi točna?
- A. pSA < pSB i pDA < pDB
- B. pSA > pSB i pDA > pDB
- C. pSA < pSB i pDA > pDB
- D. pSA > pSB i pDA < pDB
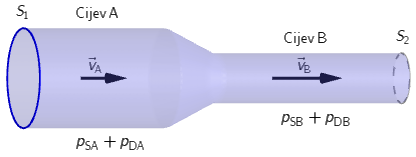
Bernoullijevu jednadžbu: \[p_{\small{\textrm{A}}}+\frac{\rho\,v_{\textrm{A}}^{2}}{2}=p_{\small{\textrm{B}}}+\frac{\rho\,v_{\textrm{B}}^{2}}{2}\] zapišimo u obliku: \[p_{\,\small{\textrm{SA}}}+p_{\,\small{\textrm{DA}}}=p_{\,\small{\textrm{SB}}}+p_{\,\small{\textrm{DB}}}\] Brzina u cijevi A je manja od brzine u cijevi B: \[v_{\,\small{\textrm{A}}} < v_{\,\small{\textrm{B}}}\] Zbog toga je i dinamički tlak u cijevi A manji nego u cijevi B: \[p_{\,\small{\textrm{DA}}} < p_{\,\small{\textrm{DB}}}\] Ukupni tlak u obje cijevi mora biti jednak pa je zato statički tlak u cijevi A veći nego u cijevi B: \[p_{\,\small{\textrm{SA}}} > p_{\,\small{\textrm{SB}}}\] Točan odgovor je D.
6. zadatak
Robert Brown promatrao je zrnca peludi u kapljici vode svjetlosnim mikroskopom.
Koja je od navedenih tvrdnja o ponašanju pojedinoga zrnca peludi vidljivoga svjetlosnim mikroskopom točna?
- A. Zrnce peludi cijelo se vrijeme giba jednoliko pravocrtno.
- B. Zrnce peludi miruje u kapljici vode jer i molekule vode u kapljici miruju.
- C. Zrnce peludi giba se nasumično jer se s njim sudaraju molekule vode koje se također nasumično gibaju.
- D. Zrnce peludi giba se nasumično samo ako je voda jako zagrijana, a miruje ako je voda sobne temperature.
Pokrenite video.
Nasumično gibanje zrnca peludi je rezultat sudara s molekulama vode koje se također nasumično gibaju.
Zrnce peludi giba se nasumično jer se s njim sudaraju molekule vode koje se također nasumično gibaju.
Točan odgovor je C.
7. zadatak
Graf ovisnosti volumena idealnoga plina o temperaturi pri stalnome tlaku plina je pravac. Na grafu je temperatura idealnoga plina nezavisna varijabla, a volumen
zavisna varijabla.
Što je od navedenoga točno za taj pravac?
- A. Pravac je paralelan s osi V.
- B. Pravac je paralelan s osi T.
- C. Nagib pravca proporcionalan je tlaku plina.
- D. Nagib pravca obrnuto je proporcionalan tlaku plina
Primijenite jednadžbu stanja idealnog plina: \[pV=n\,R\,T\] za izobarni proces.
Jednadžbu stanja plina prikažimo u obliku:
\[V=\frac{n\,R}{p}\,T\]
Nagib ovog pravca je:
\[\frac{n\,R}{p}\]
Vidimo da je nagib pravca obrnuto proporcionalan s p.
Točan odgovor je D.
8. zadatak
Dvije jednake bakrene kocke, od kojih je jedna temperature 20 oC, a druga temperature
50 oC, dovedu se u kontakt.
Na kojoj će temperaturi prestati izmjena topline među kockama?
Zanemarite gubitak topline u okolinu.
- A. 15 oC
- B. 30 oC
- C. 35 oC
- D. 50 oC
Toplina će prelaziti s toplije na hladniju kocku sve dok ne nastupi toplinska ravnoteža. Tada će obje kocke imati jednaku temperaturu.
Označimo temperaturu toplinske ravnoteže s t. Toplija kocka se ohladila od temperature 50 oC do temperature t jer je predala toplinu hladnijoj kocki: \[Q_{1}=m\,c\,\left(50-t\right)\] Hladnija kocka se zagrijala od temperature 20 oC do temperature t jer je primila toplinu od toplije kocke: \[Q_{2}=m\,c\,\left(t-20\right)\] \begin{matrix} \begin{align*} &Q_{1}=Q_{2}\\ &m\,c\,\left(50-t\right)=m\,c\,\left(t-20\right)\\ &50-t=t-20\\ &t=35\,^{\textrm{o}}\textrm{C} \end{align*} \end{matrix} Točan odgovor je C.
9. zadatak
Toplinski stroj tijekom svakoga kružnog ciklusa izvrši rad 100 J na okolinu i pritom hladnijemu
spremniku preda 500 J energije.
Kolika je korisnost toga toplinskog stroja?
Zanemarite gubitke energije u okolinu.
- A. 17 %
- B. 20 %
- C. 80 %
- D. 83 %
Toplinski stroj u kružnom procesu od toplijeg spremnika prima toplinu Q1. Jedan dio te topline, Q2, predaje hladnijem spremniku, a drugi dio pretvara u rad, W. U kružnom se procesu plin vraća u početno stanje pa je promjena unutarnje energije jednaka nuli: ΔU = 0.
Koristan rad kojega stroj obavi: \[W=Q_{1}-\left | Q_{2} \right |\] Korisnost toplinskog stroja, η , definiramo kao omjer korisnog rada i uložene energije: \[\eta =\frac{W}{Q_{1}}\] ili \[\eta =\frac{Q_{1}-\left | Q_{2} \right |}{Q_{1}}\]
Toplina koju plin prima od toplijeg spremnika: \[Q_{1}=W+\left | Q_{2} \right |=100+500=600\,\textrm{J}\] \[\eta =\frac{W}{Q_{1}}=\frac{100}{600}=0,16666\] \[\eta =16,7 \%\approx 17 \%\] Točan odgovor je A.
10. zadatak
Na slici je prikazana metalna pozitivno nabijena šuplja kugla.
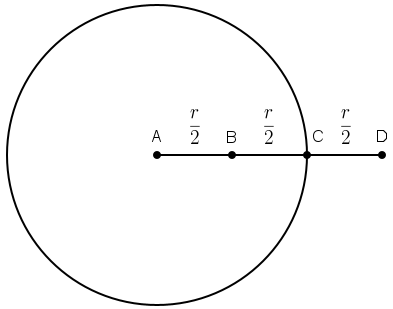
Točka C nalazi se na vanjskoj površini kugle.
Koja je od navedenih tvrdnja za iznos električnoga polja u točkama A, B, C i D točna?
- A. EA > EB > EC > ED
- B. EB = EC = EA > ED
- C. EC > ED > EA = EB
- D. EA = EB = EC = ED
U bilo kojoj točki unutar metalne sfere (šuplje kugle) električno polje jednako je nuli.
Na površini sfere električno polje jednako je:
\[E=k\,\frac{Q}{R^2}\]
gdje je R polumjer sfere, a Q naboj sfere.
U točkama izvan sfere na udaljenosti r od središta (r > R) električno polje jednako je:
\[E=k\,\frac{Q}{r^2}\]
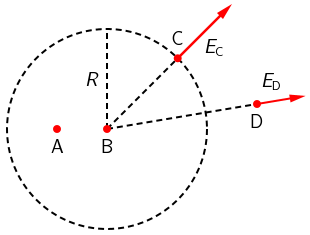
Točke A i B su unutar nabijene sfere pa je električno polje u njima jednako nuli: \[E_\textrm{A}=E_\textrm{B}=0\] Točka C manje je udaljena od središta sfere od točke D pa je: \[E_\textrm{C} > E_\textrm{D}=0\] Točan odgovor je C.
11. zadatak
Kondenzator s paralelnim pločama priključi se na izvor napona, čime se kondenzator nabije. Kondenzator se zatim odspoji od izvora napona i nakon toga mu se između
ploča umetne dielektrik.
Koja je od navedenih tvrdnja za napon među pločama i pohranjenu električnu potencijalnu energiju u kondenzatoru točna?
- A. Smanjuju se napon i električna potencijalna energija.
- B. Povećavaju se napon i električna potencijalna energija.
- C. Smanjuje se napon, a povećava se električna potencijalna energija.
- D. Povećava se napon, a smanjuje se električna potencijalna energija.
Kada se kondenzator s paralelnim pločama napuni i zatim odspoji od izvora napona, primijenimo zakon očuvanja naboja, prema kojemu je naboj na pločama konstantan: \[Q=\textrm{konst.}\] Umetanjem dielektrika između ploča kondenzatora, kapacitet kondenzatora se povećava: \[C=\large\varepsilon_{0}\,\varepsilon_{r}\normalsize \,\frac {S}{d}\]
Iz izraza za naboj na pločama: \[Q=C\,U\] zaključijemo da će se napon između ploča: \[U=\frac{Q}{C}\] smanjiti jer je naboj na pločama konstantan, a kapacitet se povećao.
Električna potencijalna energija kondenzatora jednaka je radu nabijanja kondenzatora:
\[W=\frac{1}{2}Q\,U\]
Zbog smanjenja napona između ploča kondenzatora, smanjila se i njegova električna potencijalna energija.
Točan odgovor je A.
12. zadatak
Otpornik nepoznatoga otpora R spojen je s otpornikom otpora 18 Ω tako da njihov ukupan
otpor iznosi 6 Ω.
Kako su spojeni otpornici i koliki je iznos otpora R?
- A. Otpornici su spojeni serijski i R = 9 Ω.
- B. Otpornici su spojeni serijski i R = 11 Ω.
- C. Otpornici su spojeni paralelno i R = 9 Ω.
- D. Otpornici su spojeni paralelno i R = 11 Ω.
Ukupan otpor, Ruk , paralelno spojenih otpornika R1 i R2 manji je i od R1 i od R2: \begin{matrix} \begin{align*} &\frac{1}{R_\textrm{uk}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}\\ &R_\textrm{uk}=\frac{R_1\,R_2}{R_1+R_2} \end{align*} \end{matrix}
Ukupan otpor, Ruk , serijski spojenih otpornika R1 i R2 veći je i od R1 i od R2: \[R_\textrm{uk}=R_1+R_2\]
Otpornici su spojeni paralelno: \begin{matrix} \begin{align*} &R_\textrm{uk}=\frac{R_1\,R_2}{R_1+R_2}\\ &R_1=R\\ &R_2=18\,\Omega\\ &R_\textrm{uk}=6\,\Omega\\ &\frac{R\cdot 18}{R+18}=6\\ &3\,R=R+18\\ &R=9\,\Omega \end{align*} \end{matrix}
Točan odgovor je C.
13. zadatak
Vodljivi prsten nalazi se u homogenome magnetskom polju indukcije B usmjerenom vertikalno prema gore.
Pri kojem će se od navedenih gibanja prstena u njemu inducirati struja?
- A. Prsten se rotira oko vertikalne osi.
- B. Prsten slobodno pada i ne rotira se.
- C. Prsten se rotira oko horizontalne osi.
- D. Prsten se giba jednoliko i ne rotira se.
Pokrenite video.
Pri rotaciji prstena oko vertikalne osi magnetski tok kroz prsten ne mijenja se pa na osnovu Faradayevog zakona zaključujemo kako se neće inducirati struja
kroz prsten.
Pokrenite video.
Pri slobodnom padu prstena magnetski tok kroz prsten ne mijenja se pa na osnovu Faradayevog zakona zaključujemo kako se neće inducirati struja
kroz prsten.
Pokrenite video.
Pri rotaciji prstena oko horizontalne osi magnetski tok kroz prsten se mijenja pa na osnovu Faradayevog zakona zaključujemo kako će se u prstanu inducirati struja.
To je točan odgovor.
Pokrenite video.
Dok je prsten cijelom površinom u magnetskom polju magnetski tok kroz prsten ne mijenja se pa na osnovu Faradayevog zakona zaključujemo kako se neće inducirati struja
kroz prsten. Struja će se inducirati tek kada prsten bude izlazio iz magnetskog polja.
Zbog neprecizno formuliranog zadatka i ovo rješenje moglo bi se prihvatiti kao točno.
14. zadatak
Na slici su prikazana tri paralelna, međusobno jednako udaljena i beskonačno duga vodiča kojima prolaze jednake struje
I u naznačenome smjeru.
Koja od ponuđenih slika točno prikazuje vektor ukupne magnetske sile kojom gornja dva vodiča djeluju na donji vodič?
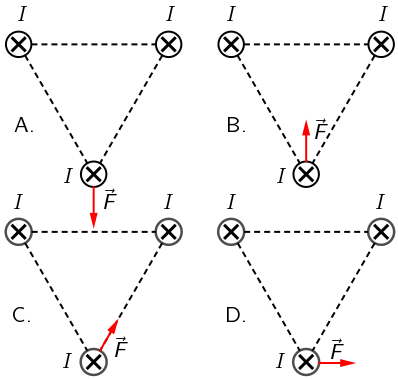
- A. Slika A.
- B. Slika B.
- C. Slika C.
- D. Slika D.
Kroz dva vrlo duga ravna i paralelna vodiča prolaze struje I1 i
I2. Udaljenost između vodića je r.
Sila kojom međusobno djeluju dijelovi vodiča duljine ℓ:
\[F=\frac{\mu_{0}\,\mu_{r}}{2\pi}\,\frac{I_{1}\,I_{2}\,\ell}{r}\]
Ako su struje jednako orijentirane, sila je privlačna:
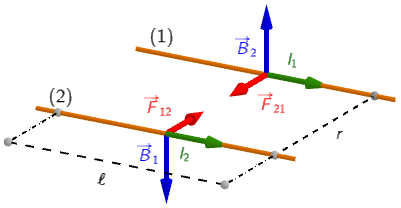
Ako su struje suprotno orijentirane, sila je odbojna:
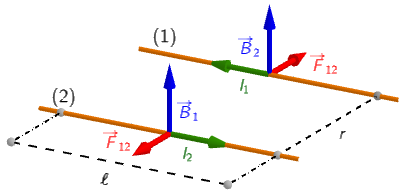
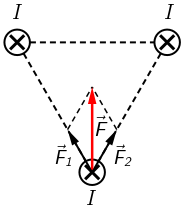
Struje su jednako orijentirane pa se bilo koja dva vodiča privlače. Gornji vodiči djeluju silama \(\vec{F}_1\) i \(\vec{F}_2\) na donji vodič.
Rezultanta tih sila označena je crveno obojenim vektorom.
Točan odgovor je B.
15. zadatak
Učenik mjeri najveću brzinu v bloka mase m koji je ovješen na idealnu oprugu i koji harmonijski
titra amplitudom A.
Ako se blok zamijeni blokom mase 2m, ali amplituda titranja ostane jednaka, koliko iznosi maksimalna brzina bloka mase
2m?
- A. \(2\,v\)
- B. \(v/\sqrt{2}\)
- C. \(v/2\)
- D. \(v/4\)
Čestica će harmonijski titrati ako na nju djeluje harmonijska sila:
\[\vec{F}=-k\,\vec{y}\]
Preznak minus znači da je orijentacija harmonijske sile suprotna orijentaciji elongacije.
Harmonijsku konstantu k može se prikazati:
\[k=m\,\omega^{2}\]
jednadžba brzine pri harmonijskom titranju:
v=v_{0}\,\textrm{cos}\left(\omega t+\varphi_{0} \right)
Maksimalna brzina harmonijskog titranja: \[v_{0}=\omega\,A\] \begin{matrix} \begin{align*} &k=m\,\omega^{2}\\ &\omega=\sqrt{\frac{k}{m}}\\ &v_{0}=A\,\omega\\ &v_{0}=A\,\sqrt{\frac{k}{m}}\\ &v'_{0}=A\,\sqrt{\frac{k}{2\,m}}\\ &v'_{0}=\frac{1}{\sqrt{2}}\,A\,\sqrt{\frac{k}{m}}\\ &v'_{0}=\frac{v_{0}}{\sqrt{2}} \end{align*} \end{matrix} Točan odgovor je B.
16. zadatak
Dva ravna vala istih valnih duljina šire se kroz isti medij. Za odnos amplituda valova vrijedi
A2 = 3A1.
Kako se odnose energije valova?
- A. \(\Large\frac{E_{2}}{E_{1}}\normalsize{=}\frac{\Large{1}}{\Large{3}}\)
- B. \(\Large\frac{E_{2}}{E_{1}}\normalsize{=1}\)
- C. \(\Large\frac{E_{2}}{E_{1}}\normalsize{=3}\)
- D. \(\Large\frac{E_{2}}{E_{1}}\normalsize{=9}\)
Energija mehaničkog vala koji se širi sredstvom, npr. napetim užetom ili žicom, proporcionalna je kvadratu amplitude vala: \[E=\frac{1}{2}\,\rho\,A^{2}\,\omega^{2}\,\lambda\]
- \(\rho\) - gustoća sredstva
- \(A\) - amplituda vala
- \(\omega=\Large{\frac{2\,\pi}{T}}\) - kutna frekvencija
- \(\lambda\) - valna duljina
Zapišimo energije oba vala i zatim prvu jednadžbu podijelimo drugom: \begin{matrix} \begin{align*} &E_{2}=\frac{1}{2}\,\rho\,A_{2}^{\;2}\,\omega^{2}\,\lambda\\ &E_{1}=\frac{1}{2}\,\rho\,A_{1}^{\;2}\,\omega^{2}\,\lambda\\ &\frac{E_{2}}{E_{1}}=\frac{1/2}{1/2}\,\frac{\rho\,A_{2}^{\;2}\,\omega^{2}\,\lambda}{\rho\,A_{1}^{\;2}\,\omega^{2}\,\lambda}\\ &\frac{E_{2}}{E_{1}}=\left(\frac{A_{2}}{A_{1}}\right)^{2}\\ &\frac{E_{2}}{E_{1}}=\left(\frac{3\,A_{1}}{A_{1}}\right)^{2}\\ &\frac{E_{2}}{E_{1}}=9 \end{align*} \end{matrix} Točan odgovor je D.
17. zadatak
Na slici je prikazan stojni val frekvencije 550 Hz koji nastaje na napetoj niti.
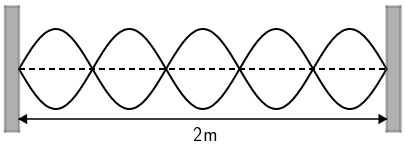
Koliko iznosi brzina valova na toj niti?
- A. 1100 m/s
- B. 550 m/s
- C. 440 m/s
- D. 275 m/s
Dva transverzalna harmonijska vala šire se kroz isto sredstvo, npr. kroz napetu žicu ili elastično uže. Valovi imaju jednaku amplitudu, valnu duljinu i frekvenciju, ali se šire u suprotnom smjeru. Interferencijom takvih valova nastaje stojni val koji ima jednaku valnu duljinu kao i valovi od kojih je nastao.
Na duljini od 2 m smjestile su se 2,5 valne duljine. \[\lambda=\frac{2}{2,5}=0,8\,\textrm{m}\] Brzina valova od kojih je nastao stojni val: \begin{matrix} \begin{align*} &v=f\,\lambda\\ &v=550\cdot 0,8\\ &v=440\,\textrm{m/s} \end{align*} \end{matrix} Točan odgovor je C.
18. zadatak
Liječnik se koristi svjetlovodom u endoskopu za pregled unutarnjih organa.
Koji je od navedenih fizičkih principa najvažniji za rad svjetlovoda u endoskopu?
- A. totalna refleksija svjetlosti
- B. interferencija svjetlosti
- C. polarizacija svjetlosti.
- D. disperzija svjetlosti
Kamera na kraju endoskopa prenosi slike unutrašnjosti tijela na monitor, omogućujući liječnicima gledanje unutarnjih organa i tkiva u stvarnom vremenu.
Fleksibilna cijev omogućuje endoskopu da se savija i prolazi kroz zakrivljene dijelove tijela, poput probavnog trakta. Optička vlakna omogućuju totalnu refleksiju pa svjetlost može doći do organa i kada je cijev zakrivljena.
Točan odgovor je A.
19. zadatak
Koja je od navedenih tvrdnja točna za radiovalove i valove vidljive svjetlosti koji se šire u istome sredstvu?
- A. Radiovalovi imaju veću brzinu od valova vidljive svjetlosti.
- B. Radiovalovi imaju manju brzinu od valova vidljive svjetlosti.
- C. Radiovalovi imaju manju frekvenciju od valova vidljive svjetlosti.
- D. Radiovalovi imaju manju valnu duljinu od valova vidljive svjetlosti.
Radiovalovi i valovi vidljive svjetlosti su elektromagnetski valovi. Svi elektromagnetski valovi u vakuumu imaju jednaku brzinu:
\[c=3\cdot 10^{8}\,\textrm{m/s}\]
Frekvencija radiovalova je između 3 Hz i 300 GHz.
Frekvencija vidlive svjetlosti je između 430 THz i 770 THz.
Točan odgovor je C.
20. zadatak
Određeni materijal obasjan je elektromagnetskim zračenjem energije fotona 2 eV i pritom dolazi do fotoelektričnoga učinka.
Maksimalna kinetička energija pojedinoga elektrona izbačenoga iz materijala iznosi 0,8 eV.
Koliko će iznositi maksimalna kinetička energija pojedinoga izbačenog elektrona ako se taj materijal obasja elektromagnetskim zračenjem energije fotona
2,5 eV?
- A. 0,8 eV
- B. 1,3 eV
- C. 1,7 eV
- D. 2,5 eV
Energija fotona koja pada na metal pretvara se u rad potreban za svladavanje energije vezanja elektrona u metalu i u njegovu kinetičku energiju: \[E_\textrm{f}=W_{0}+E_\textrm{k}\]
Primjenimo Einsteinovu jednadžbu za fotoelektrični učinak: \[E_\textrm{f}=W_{0}+E_\textrm{k}\] \begin{matrix} \begin{align*} &E_\textrm{f}=2\,\textrm{eV}\\ &E_\textrm{k}=0,8\,\textrm{eV}\\ &{E_\textrm{f}}^{'}=2,5\,\textrm{eV}\\ &2=W_{0}+0,8\\ &2,5=W_{0}+{E_\textrm{k}}^{'}\\ &{E_\textrm{k}}^{'}-0,8=2,5-2\\ &{E_\textrm{k}}^{'}=1,3\,\textrm{eV} \end{align*} \end{matrix} Točan odgovor je B.
21. zadatak
Elektron energije 10 eV ima valnu duljinu λ1 , a elektron energije
1000 eV ima valnu duljinu λ2.
Koliki je omjer λ1 / λ2?
- A. 1/1000
- B. 1/10
- C. 10
- D. 100
De Broglieva valna duljina: \[\lambda=\frac{h}{p}\] Kinetička energija elektrona: \[E_\textrm{k}=\frac{m\,v^{2}}{2}\] \[E_\textrm{k}=\frac{m^{2}\,v^{2}}{2\,m}\] \[E_\textrm{k}=\frac{p^{2}}{2\,m}\]
\[p=\sqrt{2\,m\,E_\textrm{k}}\] \[\lambda=\frac{h}{\sqrt{2\,m\,E_\textrm{k}}}\] \[\frac{\lambda_{1}}{\lambda_{2}}=\frac{h}{\sqrt{2\,m\,E_\textrm{k1}}}\cdot \frac{\sqrt{2\,m\,E_\textrm{k2}}}{h}\] \[\frac{\lambda_{1}}{\lambda_{2}}=\sqrt{\frac{E_\textrm{k2}}{E_\textrm{k1}}}\] \[\frac{\lambda_{1}}{\lambda_{2}}=10\] Točan odgovor je C.
22. zadatak
Koji je od navedenih znanstvenika eksperimentalno utvrdio da se atom sastoji od uglavnom praznoga prostora s malom, gustom, pozitivnom jezgrom?
- A. Niels Bohr
- B. James Chadwick
- C. Ernest Rutherford
- D. Joseph John Thomson
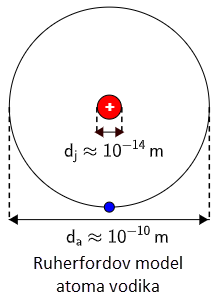
Na osnovu eksperimenata koje je izvodio, Rutherford je zaključio da pozitivni naboj atoma nije raspoređen po cijelom atomu, kako je predviđao Thomsonov model,
nego u jednom njegovom malenom dijelu, koji se nalazi u središtu atoma i koji je nazvan jezgra atoma. Elektroni se gibaju po kružnicama kojima je središte u jezgri,
slično kao što se planeti gibaju oko Sunca pa je ovaj model nazvan i planetarnim modelom. Promjer jezgre je oko 10000 puta manji od promjera atoma, a u njoj je
koncentrirana gotovo sva masa atoma.
Alfa raspad
\[{_\textrm{Z}^\textrm{A}}\,\textrm{X}\rightarrow {_{\textrm{Z}\texttt{-}2}^{\textrm{A-4}}}\,\textrm{Y}+{_{2}^{4}}\,\textrm{He}\]
Jedino pri Točan odgovor je C.
23. zadatak
Koji je od navedenih raspada reakcija fisije?
- A. α - raspad
- B. β+ - raspad
- C. β− - raspad
- D. γ - raspad
Fisija je nuklearna reakcija pri kojoj projektil razdijeli jezgru na dva podjednaka dijela uz oslobađanje nekoliko neutrona. Ti neutroni mogu pogoditi druge jezgre i tako izazvati nove fisije. U svakoj se fisiji oslobađa energija. Jezgre s velikim brojem protona su pogodne za fisiju. Električna sila između protona je zbog male udaljenosti između njih ogromna, no jezgra se ipak ne razleti jer ju na okupu drži jaka sila koja djeluje između nukleona. Takve su jezgre spremne za raspad, ali potrebno je malo povećati razmak između protona kako bi jaka sila, koja ih drži na okupu, oslabila. To se u procesu fisije postiže gađanjem jezgre neutronima.
Alfa raspad
\[{_\textrm{Z}^\textrm{A}}\,\textrm{X}\rightarrow {_{\textrm{Z}\texttt{-}2}^{\textrm{A-4}}}\,\textrm{Y}+{_{2}^{4}}\,\textrm{He}\]
Od ponuđenih odgovora jedino pri α - raspadu nastaju dvije nove jezgre.
Točan odgovor je A.
24. zadatak
Izotop torija 230 Th raspada se α - raspadom.
Atom kojega elementa nastaje tim radioaktivnim raspadom?
- A. Pr
- B. U
- C. Ac
- D. Ra
Alfa raspad
\[{_\textrm{Z}^\textrm{A}}\,\textrm{X}\rightarrow {_{\textrm{Z}\texttt{-}2}^{\textrm{A-4}}}\,\textrm{Y}+{_{2}^{4}}\,\textrm{He}\]
Alfa raspad torija
\[{_{\,\,90}^{230}}\,\textrm{Th}\rightarrow {_{\,\,88}^{226}}\,\textrm{Ra}+{_{2}^{4}}\,\textrm{He}\] Točan odgovor je D.
25. zadatak
Idealni plin pri izobarnoj promjeni stanja izvrši rad nad okolinom iznosa 100 J. Pritom mu se volumen poveća s
1 dm3 na 2 dm3.
Koliki je tlak plina pri toj promjeni stanja?
Odgovor:
Rad plina pri stalnom tlaku: \[W=p\,\Delta V\]
\begin{matrix} \begin{align*} &p=\frac{W}{\Delta V}\\ &p=\frac{100}{\left(2\cdot 10^{-3}-10^{-3} \right)}\\ &p=10^{5}\,\textrm{Pa} \end{align*} \end{matrix}
26. zadatak
Na slici je prikazana ovisnost induktivnoga otpora o kružnoj frekvenciji.
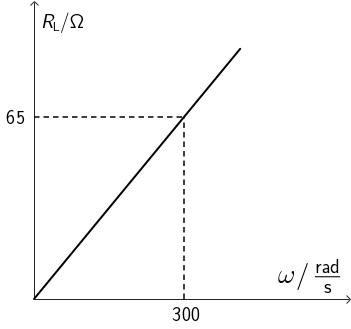
Koliki je induktivitet zavojnice?
Odgovor:
Induktivni otpor: \[R_\textrm{L}=L\,\omega\]
27. zadatak
Mala lubenica mase 1,45 kg pada iz mirovanja. Tijekom pada od 80 cm 10 % mehaničke energije lubenice
gubi se na otpor zraka.
Koliki je iznos mehaničke energije lubenice nakon prijeđenih 80 cm?
Odgovor:
Lubenica pada iz mirovanja, što znači da je početna kinetička energija nula. Početna mehanička energija lubenice je: \[E_{1}=m\,g\,h\] Deset posto početne mehaničke energije pretvori se u rad na svladavanju otpora zraka: \[W_\textrm{oz}=0,1\,E_{1}\]
Primijenimo zakon očuvanja mehaničke energije: \begin{matrix} \begin{align*} &E_{1}=W_\textrm{oz}+E_{2}\\ &E_{2}=E_{1}-W_\textrm{oz}\\ &E_{2}=m\,g\,h-0,1\,m\,g\,h\\ &E_{2}=0,9\,m\,g\,h\\ &E_{2}=10,24\,\textrm{J} \end{align*} \end{matrix}
28. zadatak
Na dnu trupa jedrilice nastala je rupa površine 2 cm2 zbog koje morska voda prodire u unutrašnjost jedrilice.
Rupa se nalazi na dubini 1,2 m ispod površine mora.
Kolikom najmanjom silom treba djelovati na čep kojim se s unutarnje strane zatvara rupa kako bi se zaustavilo prodiranje vode?
Gustoća morske vode iznosi 1020 kg/m3.
Odgovor:
Hidrostatski tlak na dubini h ispod površine: \[p=\rho\,g\,h\] Tlak je jednak sili koja djeluje na jediničnu površinu, zbog čega je sila kojom moramo djelovati na čep: \[F=p\,S\]
Odredimo silu: \begin{matrix} \begin{align*} &F=p\,S\\ &F=\rho\,g\,h\,S\\ &F=2,45\,\textrm{N} \end{align*} \end{matrix}
29. zadatak
Planinar zagrijava 200 g vode u aluminijskoj posudi mase 100 g. Plamenik daje
72 kJ topline u minuti koja se u potpunosti iskoristi za zagrijavanje posude i vode.
Koliko je vremena potrebno da se zagriju posuda i voda od 20 oC do
90 oC?
Specifični toplinski kapacitet aluminija iznosi 900 J/(kg K), a vode 4200 J/(kg K).
Odgovor:
Toplina potrebna za zagrijavanje tijela: \[Q=m\,c\,\Delta t\]
- \(m\)-masa tijela
- \(c\)-specifični toplinski kapacitet tijela
- \(\Delta t\)-porast temperature tijela \[\Delta t=t_\textrm{kon}-t_\textrm{poc}\]
Snaga plamenika: \[P_\textrm{pl}=\frac{72\,\textrm{kJ}}{1\,\textrm{minuta}}\] \[P_\textrm{pl}=\frac{72000\,\textrm{J}}{60\,\textrm{s}}=1200\,\textrm{W}\] Toplina koju oslobađa plamenik: \[Q_\textrm{pl}=P_\textrm{pl}\,t\] u potpunosti se pretvara u toplinu zagrijavanja posude i vode: \[Q_\textrm{pl}=Q_\textrm{al}+Q_\textrm{voda}\] \begin{matrix} \begin{align*} &Q_\textrm{pl}=Q_\textrm{al}+Q_\textrm{voda}\\ &P_\textrm{pl}\,t=m_\textrm{al}\,c_\textrm{al}\,\Delta t+m_\textrm{voda}\,c_\textrm{voda}\,\Delta t\\ &P_\textrm{pl}\,t=\left(m_\textrm{al}\,c_\textrm{al}+m_\textrm{voda}\,c_\textrm{voda}\right)\,\Delta t\\ &t=\frac{\left(m_\textrm{al}\,c_\textrm{al}+m_\textrm{voda}\,c_\textrm{voda}\right)\,\Delta t}{P_\textrm{pl}}\\ &t=\frac{\left(0,1\cdot 900+0,1\cdot 4200\right)\cdot 70}{1200}\\ &t=54,25\,\textrm{s} \end{align*} \end{matrix}
30. zadatak
Učenici su izveli Youngov pokus koristeći se dvjema pukotinama razmaknutim 70 μm, milimetarskim papirom, laserom nepoznate valne duljine i metrom. Milimetarski papir zalijepili su na vertikalni zid. Pukotine su postavili na udaljenost 4 m od zida paralelno s papirom. Laserski snop propustili su kroz pukotine te je nastala interferencijska slika na milimetarskome papiru kako je prikazano na slici.
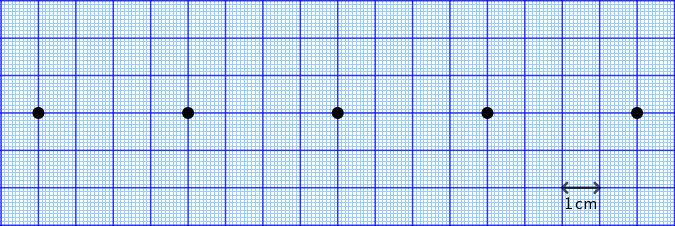
1. Koliko iznosi razmak između susjednih maksimuma?
Odgovor:
Razmak između susjednih maksimuma očitamo iz slike (razmak između susjednih točaka).
s = 4 cm.
2. Kolika je valna duljina lasera korištenoga u ovome pokusu?
Odgovor:
Valna duljina svjetlosti kod Youngovog pokusa: \[\lambda=\frac{s\,d}{a}\]
- s - udaljenost između interferencijskih maksimuma
- d - razmak između pukotina
- a - udaljenost zastora od pukotina
Valna duljina lasera korištenoga u ovome pokusu: \[\lambda=\frac{4\cdot 10^{-2}\cdot 70\cdot 10^{-6}}{4}\] \[\lambda=7\cdot 10^{-7}\,\textrm{m}\] \[\lambda=700\,\textrm{nm}\]
31. zadatak
Na slici je prikazan kamion s ravnom platformom na kojoj se nalazi sanduk. Kamion se giba uz brijeg nagiba α = 30o. Koeficijent statičkoga trenja između platforme kamiona i sanduka iznosi 0,7.
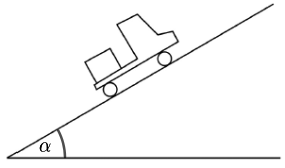
Koliko iznosi maksimalno ubrzanje koje kamion može postići prije nego što sanduk počne kliziti unatrag u odnosu na kamion?
Odgovor: \(\textrm{m}/\textrm{s}^{2}\)
Na sanduk djeluju:
- Sila teža - \(F_\textrm{g}\)
- Reakcija podloge - \(N\)
- Sila trenja - \(F_\textrm{t}\)
Odredimo sile koje djeluju na tijelo:
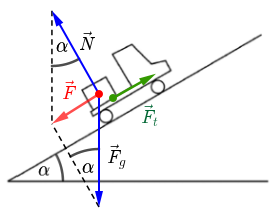
Reakcija podloge
\begin{matrix} \begin{align*} &N=F_\textrm{g}\,\textrm{cos}\,\alpha\\ &N=m\,g\,\textrm{cos}\,\alpha \end{align*} \end{matrix}Sila trenja
\begin{matrix} \begin{align*} &F_\textrm{t}=\mu_\textrm{s}\,N\\ &F_\textrm{t}=\mu_\textrm{s}\,m\,g\,\textrm{cos}\,\alpha \end{align*} \end{matrix}Rezultanta sila \(N\) i \(F_\textrm{g}\)
\begin{matrix} \begin{align*} &F=F_\textrm{g}\,\textrm{sin}\,\alpha\\ &F=m\,g\,\textrm{sin}\,\alpha \end{align*} \end{matrix}Jednadžba gibanja
\begin{matrix} \begin{align*} &m\,a=F_\textrm{t}-F\\ &m\,a=\mu_\textrm{s}\,m\,g\,\textrm{cos}\,\alpha-m\,g\,\textrm{sin}\,\alpha\\ &a=\mu_\textrm{s}\,g\,\textrm{cos}\,\alpha-g\,\textrm{sin}\,\alpha\\ &a=1,06\,\frac{\textrm{m}}{\textrm{s}^{2}} \end{align*} \end{matrix}32. zadatak
Strujni krug sastoji se od idealne baterije napona 5 V spojene na paralelni spoj dvaju identičnih otpornika. Svaki od tih otpornika
ima duljinu 1 cm i napravljen je od tanke žice od nikroma otpornosti
1,12·10-6 Ω m. Za rad strujnoga kruga baterija daje 25 W.
Kolika je površina poprečnoga presjeka žice od koje je napravljen pojedini otpornik?
Odgovor: \(\textrm{m}^{2}\)
Snaga baterije može se prikazati kao: \[P=\frac{U^{2}}{R_\textrm{uk}}\] Ruk je ukupni otpor strujnog kruga.
Ukupni otpor dva jednaka paralelno spojena otpornika: \[\frac{1}{R_\textrm{uk}}=\frac{1}{R}+\frac{1}{R}=\frac{2}{R}\]
Otpor žice: \[R = \rho \frac{\ell}{S}\]
Odredimo ukupni otpor kruga: \begin{matrix} \begin{align*} &P=\frac{U^{2}}{R_\textrm{uk}}\\ &R_\textrm{uk}=\frac{U^{2}}{P}\\ &R_\textrm{uk}=\frac{5^{2}}{25}\\ &R_\textrm{uk}=1\,\Omega\\ \end{align*} \end{matrix} Otpori su jednaki i paralelno spojeni pa je otpor svakog otpornika: \begin{matrix} \begin{align*} &\frac{1}{R_\textrm{uk}}=\frac{2}{R}\\ &R=2\,R_\textrm{uk}\\ &R=2\,\Omega \end{align*} \end{matrix} Odredimo površinu poprečnog presjeka žice od koje su načinjeni otpornici: \begin{matrix} \begin{align*} &R = \rho \frac{\ell}{S}\\ &S=\frac{\rho\,\ell}{R}\\ &S=\frac{1,12\cdot 10^{-6}\cdot 10^{-2}}{2}\\ &S=0,56\cdot 10^{-8}\,\textrm{m}^{2}\\ &S=5,6\cdot 10^{-9}\,\textrm{m}^{2}\\ \end{align*} \end{matrix}
33. zadatak
Zavojnica ima površinu poprečnoga presjeka 10 cm2, duljinu 45 cm i 250 namotaja.
Koliki je iznos induciranoga napona u zavojnici ako se struja kroz nju poveća s 1,2 A na 2,6 A u vremenu
0,07 s?
Zavojnica se nalazi u zraku.
Odgovor:
Magnetsko polje zavojnice koja se nalazi u zraku: \[B=\mu_{0}\frac{N\,I}{\ell}\] Faradayev zakon elektromagnetske indukcije: \[U_\textrm{i}=-N\frac{\Delta \Phi}{\Delta t}\] Promjenu magnetskog toka: \[\Phi=B\,S\] moguće je ostvariti promjenom magnetskog polja: \[\Delta \Phi=S\,\Delta B\] ili promjenom površine kroz koju prolaze magnetske silnice: \[\Delta \Phi=B\,\Delta S\]
Promjenu magnetskog toka u ovom primjeru ostvarujemo promjenom struje kroz zavojnicu, zbog čega se mijenja i magnetsko polje: \begin{matrix} \begin{align*} &\Delta \Phi=S\,\Delta B\\ &\Delta \Phi=S\,\frac{\mu_{0}\,N}{\ell}\,\Delta I\\ &U_\textrm{i}=-N\frac{\Delta \Phi}{\Delta t}\\ &U_\textrm{i}=-\mu_{0}\,N^{2}\frac{S}{\ell}\frac{\Delta I}{\Delta t}\\ &U=-3,49\cdot 10^{-3}\,\textrm{V}=-3,49\,\textrm{mV} \end{align*} \end{matrix}
34. zadatak
Na opruzi konstante elastičnosti 35 N/m harmonijski titra uteg amplitudom 8 cm.
Koliko iznosi elastična potencijalna energija opruge u trenutku kad tijelo ima polovinu maksimalne brzine koju može postići?
Odgovor:
Jednadžbe brzine kod harmonijskog titranja: \[v=\omega\,A\,\textrm{cos}\left(\omega\,t\right)\] Maksimalna brzina kod harmonijskog titranja: \[v_{0}=\omega\,A\] Ukupna energija harmonijskog titranja u bilo kojem trenutku jednaka je zbroju kinetičke i elastične potencijalne enegije: \[E=E_\textrm{k}+E_\textrm{p}\] \[E_\textrm{k}=\frac{1}{2}\,m\,v^{2}\] \[E_\textrm{p}=\frac{1}{2}\,k\,A^{2}\] Kada se tijelo nalazi u amplitudnome položaju elongacija titranja jednaka je amplitudi, a brzina jednaka nuli. Elastična potencijalna energija je maksimalna, dok je kinetička energija jednaka nuli: \[E=E_\textrm{p}=\frac{1}{2}\,k\,A^{2}\]
Odredimo kinaetičku energiju tijela u trenutku kada mu je brzina dva puta manja od najveće brzine. Tada ćemo iz ukupne i kinetičke energije odrediti elastičnu potencijalnu energiju: \begin{matrix} \begin{align*} &E_\textrm{k}=\frac{1}{2}\,m\,v^{2}\\ &v=\frac{1}{2}\,v_{0}\\ &v=\frac{1}{2}\,\omega\,A\\ &E_\textrm{k}=\frac{1}{2}\,m\,[\frac{1}{2}\,\omega\,A]^{2}\\ &k=m\,\omega^{2}\\ &m=\frac{k}{\omega^{2}}\\ &E_\textrm{k}=\frac{1}{2}\cdot \frac{k}{\omega^{2}}\cdot \frac{1}{4}\,\omega^{2}\,A^{2}\\ &E_\textrm{k}=\frac{1}{8}\,k\,A^{2}\\ &E_\textrm{p}=E-E_\textrm{k}\\ &E=\frac{1}{2}\,k\,A^{2}\\ &E_\textrm{p}=\frac{1}{2}\,k\,A^{2}-\frac{1}{8}\,k\,A^{2}\\ &E_\textrm{p}=\frac{3}{8}\,k\,A^{2}\\ &E_\textrm{p}=0,084\,\textrm{J}\\ \end{align*} \end{matrix}
35. zadatak
Vrijeme života piona mjereno u sustavu u kojemu on miruje iznosi 26 ns. Neki pion stvoren je visoko u atmosferi tako da se odmah približava prema tlu brzinom 0,95 c.
1. Koliko je vrijeme života piona mjereno iz sustava promatrača na Zemlji?
Odgovor:
Vrijeme života piona mjereno iz sustava promatrača na Zemlji: \[t=\frac{t_{0}}{\sqrt{1-v^{2}/c^{2}}}\]
\begin{matrix} \begin{align*} &t_{0}=26\,\textrm{ns}=2,6\cdot 10^{-8}\,\textrm{s}\\ &v=0,95\,c\\ &t=\frac{t_{0}}{\sqrt{1-v^{2}/c^{2}}}\\ &t=\frac{2,6\cdot 10^{-8}}{\sqrt{1-0,95^{2}}}\\ &t=8,33\cdot 10^{-8}\,\textrm{s}=83,3\,\textrm{ns} \end{align*} \end{matrix}
2. Kolika je udaljenost koju će pion prijeći mjerena iz sustava promatrača na Zemlji?
Odgovor:
Udaljenost koju će pion prijeći mjerena iz sustava promatrača na Zemlji: \begin{matrix} \begin{align*} &s=v\cdot t\\ \end{align*} \end{matrix}
U sustavu promatrača na Zemlji pion prelazi udaljenost: \begin{matrix} \begin{align*} &s=v\cdot t\\ &s=0,95\,c\cdot 8,33\cdot 10^{-8}\\ &s=23,74\,\textrm{m} \end{align*} \end{matrix}