Osnovni postulati specijalne teorije relativnosti
- Princip relativnosti
Svi zakoni fizike u svim inercijalnim sustavima imaju jednak oblik. - Konstantnost brzine svjetlosti
Brzina svjetlosti u svim inercijalnim sustavima je konstantna i za vakuum iznosi približno c = 3·108 m/s.
Einstein je pokazao da ova dva postulata nisu proturječna, kako je izgledalo u klasičnoj fizici, nego da, uzeta zajedno, objašnjavaju sve poteškoće klasične fizike, a i predviđaju niz posljedica koje su kasnije bile eksperimentalno provjerene. Polazeći od ova dva postulata, Einstein je izgradio specijalnu teoriju relativnosti.
Primjetimo da je drugi postulat uključen u prvi. Kada brzina svjetlosti ne bi bila konstantna, mjerenjem te brzine mogli bismo ustanoviti da li se nalazimo u sustavu koji miruje ili se giba jednoliko pravocrtno.
Kontrakcija duljine
Uzmimo štap duljine L0 koji u sustavu S miruje i postavljen je paralelno sa osi x. Koordinate krajnjih točaka štapa su x1 i x2, tako da je L0 = x2 - x1. Te je koordinate odredio promatrač u sustavu S u odnosu na kojega štap miruje, koristeći svoj metar. Duljinu koju je odredio promatrač u odnosu na kojega štap miruje, L0, nazivamo vlastitom duljinom, a duljinu L, u sustavu u odnosu na kojega se štap giba, jednostavno duljinom.
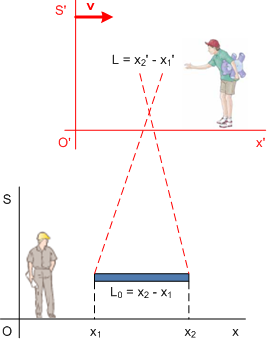
U sustavu S' promatrač mjeri krajnje točke štapa i dobija vrijednosti x1' i x2', pa za duljinu štapa dobije L = x2' - x1'. Važno je naglasiti da je promatrač u sustavu S' odredio krajnje točke štapa, x1' i x2' u istom trenutku, pa je t1' = t2'.
Ukoliko sada za transformacije koordinata uzmemo Lorentzove transformacije, za duljinu štapa u sustavu S', dobit ćemo:
$$L=L_{0}\sqrt{1-v^{2}/c^{2}}$$
Brzinu promatrača u odnosu na štap koji miruje označili smo sa v. Isti izraz vrijedi i ako promatrač miruje a štap se u odnosu na njega, u smjeru uzdužne osi, giba brzinom v.
Budući da je brzina uvijek manja od brzine svjetlosti, možemo zaključiti:
$$u < c \Rightarrow \sqrt{1-v^{2}/c^{2}}<1\Rightarrow L < L_{0}$$
Promatrač koji se u odnosu na štap giba (ili u odnosu na kojega se štap giba), zaključuje da je duljina štapa manja od duljine koju izmjeri promatrač koji u odnosu na štap miruje. Ovo nazivamo kontrakcijom duljine.
Kontrakcija duljine - aplet
Dilatacija vremena
Neka se u točki A sustava S' dogodio neki događaj, recimo svjetlosni bljesak. Početak događaja bio je u trenutku t1', a kraj u trenutku t2'. Trajanje događaja u sustavu S' je Δt0 = t2' - t1'. Trajanje događaja u sustavu S je Δt = t2 - t1. Budući da se događaj dogodio u istoj točki sustava S', slijedi da je x2' = x1'.
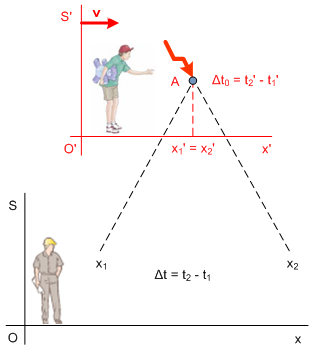
Pomoću Lorentzovih transformacija za vrijeme, dobijemo da je trajanje događaja za promatrača u sustavu S jednako:
$$\Delta t=\frac{\Delta t_{0}}{\sqrt{1-v^{2}/c^{2}}}$$
Budući da je brzina uvijek manja od brzine svjetlosti, možemo zaključiti:
$$u < c \Rightarrow \sqrt{1-v^{2}/c^{2}}<1\Rightarrow \Delta t > \Delta t_{0}$$
Trajanje događaja, mjereno satima promatrača u odnosu na kojega se točka u kojoj se događaj odvija giba, veće je od trajanja toga događaja u sustavu u kojemu ta točka miruje. Ovo nazivamo dilatacijom vremena.
Trajanje događaja u sustavu S', Δ t0, nazivamo vlastiti interval vremena ili vlastito vrijeme.
NapomenaU knjižici formula za državnu matura, ova se formula zapisuje ovako:
$$T=\frac{T_{0}}{\sqrt{1-v^{2}/c^{2}}}$$
Dilatacija vremena - aplet
Relativistička energija
Svaka čestica koja ima masu i svako tijelo imaju energiju koja je povezana s njihovom masom. To je najpoznatije Einsteinovo otkriće u specijalnoj teoriji relativnosti.
$$E=mc^2$$
Ovu energiju nazivamo vlastitom energijom. To je ujedno i jedina energija ako tijelo miruje.
Ako se tijelo giba, osim vlastite ima i kinetičku energiju, pa mu je ukupna energija jednaka:
$$E=E_{0}+E_{k}$$
Možese pokazati da ukupnu energiju možemo prikazati kao:
$$E=\frac{mc^{2}}{\sqrt{1-v^{2}/c^{2}}}$$
Ovaj nam izraz pokazuje da je masa zapravo jedan oblik energije. Kažemo da su masa i energija ekvivalentni.
U nuklearnoj fizici i fizici elementarnih čestica, puno su puta opažene pretvorbe energije u čestice (koje imaju masu) i "nestajanje" čestica uz oslobađanje energije, npr. pri anihilacija čestica i antičestica. U svim tim pokusima potvrđena je Einsteinova jednadžba koja povezuje masu i energiju.
Kinetičku energiju možemo prikazati kao razliku ukupne i vlastite energije:
$$E=\frac{mc^{2}}{\sqrt{1-v^{2}/c^{2}}}-mc^{2}$$