Ogledni ispit za maturu 2010. godine
1. zadatak
Tijelo se giba jednoliko ubrzano po pravcu. Što od navedenoga vrijedi za iznos ukupne sile na tijelo tijekom gibanja?
- A. Iznos ukupne sile na tijelo jednoliko raste.
- B. Iznos ukupne sile na tijelo jednak je nuli.
- C. Iznos ukupne sile na tijelo se jednoliko smanjuje.
- D. Iznos ukupne sile na tijelo je stalan i različit od nule.
Primijenite temeljni zakon gibanja.
Tijelo na koje djeluje stalna sila giba se jednoliko ubrzano akceleracijom: \[a=\frac{F}{m}\]
2. zadatak
Graf prikazuje ovisnost brzine tijela o vremenu pri pravocrtnom gibanju.
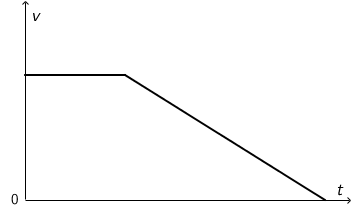
Koji \(a,t\) graf odgovara gibanju prikazanomu \(v,t\) grafom?
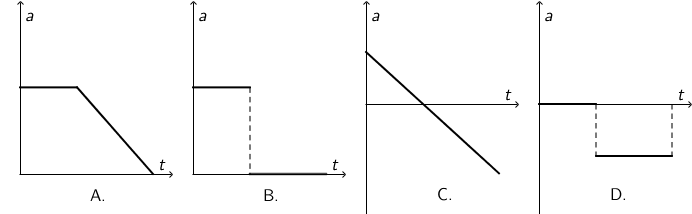
- A. Graf A.
- B. Graf B.
- C. Graf C.
- D. Graf D.
Iz zadanog \(v,t\) grafa zaključujemo da se tijelo giba jednoliko pa zatim jednoliko usporeno.
Jednoliko pa zatim jednoliko usporeno gibanje prikazano je \(a,t\) grafom D.
3. zadatak
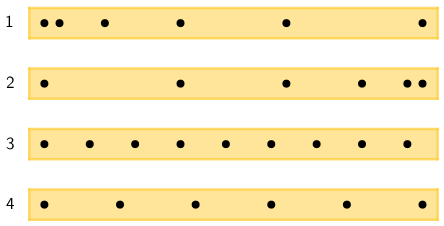
Na slici su prikazana četiri zapisa gibanja kolica dobivena pomoću elektromagnetskoga tipkala koje ostavlja trag u jednakim vremenskim razmacima.
U kojim je gibanjima srednja akceleracija kolica bila najbliža nuli?
- A. 1 i 2
- B. 1 i 3
- C. 3 i 4
- D. 2 i 4
Kod jednolikog gibanja akceleracija je jednaka nuli, a to znači da su razmaci između tragova na vrpci jednaki.
- Jednoliko ubrzano gibanje.
- Jednoliko usporeno gibanje.
- Jednoliko gibanje.
- Jednoliko gibanje.
4. zadatak
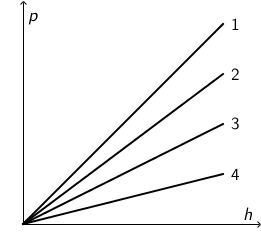
Graf prikazuje ovisnost hidrostatskoga tlaka \(p\) o dubini \(h\) za četiri tekućine označene brojevima 1, 2, 3 i 4 koje su različitih gustoća.
Kojim je grafom prikazana tekućina najmanje gustoće?
- A. 1
- B. 2
- C. 3
- D. 4
Hidrostatski tlak na tijelo koje se nalazi na dubini \(h\) u tekućini gustoće \(\rho\): \[p=\rho\,g\,h\]
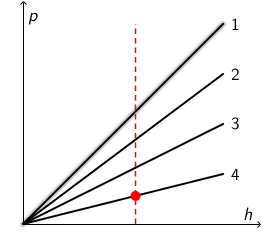
Iz grafa vidimo da je tlak koji djeluje na isto tijelo koje se nalazi u sve četiri tekućine najmanji u tekućini 4. Hidrostatski je tlak proporcionalan
gustoći tekućine pa, prema tome, tekućina 4 ima najmanju gustoću.
5. zadatak
Komunikacijski satelit kruži na udaljenosti \(R\) od središta Zemlje. Zamijenimo li satelit novim, koji je dva puta veće mase, a istog ophodnoga vremena, koliko će iznositi udaljenost novog satelita od središta Zemlje?
- A. \(R/2\)
- B. \(R\)
- C. \(\sqrt{2}\,R\)
- D. \(2\,R\)
Da bi se satelit mase \(m\) gibao oko Zemlje mase \(M\) po kružnici na njega mora djelovati centripetalna sila: \[F_{\textrm{c}}=\frac{m\,v^{2}}{R}\] Obodna brzina satelita je: \[v=\frac{2\,R\,\pi}{T}\] \[F_{\textrm{c}}=\frac{4\,\pi^{2}\,R\,m}{T^{2}}\] Ulogu centripetalne sile ima gravitacijska sila Zemlje: \[F=G\,\frac{m\,M}{R^{2}}\]
\[F_{\textrm{c}}=F\] \[\frac{4\,\pi^{2}\,R\,m}{T^{2}}=G\,\frac{m\,M}{R^{2}}\] \[R=\sqrt[3]{G\,\frac{M\,T^{2}}{4\,\pi^{2}}}\] Vidimo da udaljenost od središta Zemlje, na kojoj satelit kruži, ne ovisi o masi satelita \(m\). Prema tome, točan je odgovor B.
6. zadatak
Srednja kinetička energija čestica plina pri temperaturi \(T\) iznosi \(\bar{E}_{\textrm{k}}.\)
Pri kojoj će temperaturi srednja kinetička energija čestica plina biti dvostruko veća?
- A. \(T/2\)
- B. \(2\,T/3\)
- C. \(3\,T/2\)
- D. \(2\,T\)
Srednja kinetička energija molekula jednoatomnog idealnog plina: \[\bar{E}_{\textrm{k}}=\frac{3}{2}\,k\,T\] Srednja kinetička energija molekula dvoatomnog idealnog plina: \[\bar{E}_{\textrm{k}}=\frac{5}{2}\,k\,T\]
Srednja kinetička energija molekula idealnog plina proporcionalna je termodinamičkoj temperaturi. Ako se srednja kinetička energija čestica plina poveća dva puta, temperatura će se također povećati dva puta.
7. zadatak
U krug izmjenične struje serijski su spojeni otpornik, zavojnica i kondenzator. Pri frekvenciji 100 Hz induktivni je otpor
četiri puta veći od kapacitivnoga.
Pri kojoj će frekvenciji nastupiti rezonancija u tom strujnom krugu?
- A. 25 Hz
- B. 50 Hz
- C. 100 Hz
- D. 200 Hz
Induktivni otpor: \[R_{\small{\textrm{L}}}=L\,\omega\] Kapacitivni otpor: \[R_{\small{\textrm{C}}}=\frac{1}{C\,\omega}\] Do rezonancije (struja koja prolazi krugom je maksimalna) dolazi ako je: \[R_{\small{\textrm{L}}}=R_{\small{\textrm{C}}}\]
Do rezonancije dolazi ako je: \[R_{\small{\textrm{L}}}=R_{\small{\textrm{C}}}\] Označimo rezonantnu frekvenciju s \(\omega_{0}.\) \[L\,\omega_{0}=\frac{1}{C\,\omega_{0}}\] \[L\,C=\frac{1}{\omega_{0}^{2}}\qquad(1)\] Pri frekvenciji \(f=100\,\textrm{Hz}\) induktivni otpor četiri je puta veći od kapacitivnog: \[R_{\small{\textrm{L}}}=4\,R_{\small{\textrm{C}}}\] \[L\,\omega=\frac{4}{C\,\omega}\] \[L\,C=\frac{4}{\omega^{2}}\qquad(2)\] Izrazi (1) i (2) imaju jednake lijeve strane pa im desne strane moraju biti jednake: \[\frac{1}{\omega_{0}^{2}}=\frac{4}{\omega^{2}}\] \[\frac{1}{\omega_{0}}=\frac{2}{\omega}\] Rezonantna frekvenecija je: \[\omega_{0}=\frac{\omega}{2}\] \[2\,\pi\,f_{0}=\frac{2\,\pi\,f}{2}\] \[f_{0}=\frac{f}{2}=\frac{100}{2}=50\,\textrm{Hz}\]
8. zadatak
Dvije metalne kugle jednakih dimenzija električki su nabijene. Kugla A ima naboj +2 e, a kugla B naboj -4 e. Kugle dovedemo u međusobni kontakt. Pri tome će kugla A:
- A. dobiti 3 protona
- B. izgubiti 3 protona
- C. dobiti 3 elektrona
- D. izgubiti 3 elektrona
Primijenite zakon očuvanja električnog naboja.
Nakon dodirivanja kugle će imati jednak potencijal:
\[\varphi=k\,\frac{q}{R^{2}}\]
Kugle su jednake pa su im i polumjeri jednaki. Zbog jednakog potencijala zaključujemo da će im i naboji biti jednaki.
Zbog očuvanja naboja ukupni naboj kugli A i B prije dodirivanja bio je +2 e + -4 e = -2 e. Toliki mora biti ukupan naboj
i nakon dodirivanja pa će naboj svake kugle biti -1 e.
Naboj kugle A prije dodirivanja bio je +2 e, a nakon dodirivanja -1 e. To znači da je
kugla A dobila tri elektrona.
9. zadatak
Dva otpornika, otpora \(2\,R\) i \(3\,R\), spojena su serijski s baterijom elektromotornoga napona \(E = 30\, \textrm{V}\) i unutrašnjega otpora \(R\) kako je prikazano na slici.
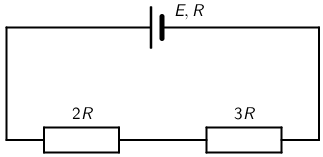
Koliko iznosi napon na otporiniku \(2\,R?\)
- A. 5 V
- B. 10 V
- C. 20 V
- D. 30 V
Ukupan otpor serijski spojenih otpornika: \[R_{\textrm{uk}}=R_{1}+R_{2}+R_{3}\,+\,...\] Ohmov zakon za cijeli strujni krug: \[I=\frac{E}{R_{\textrm{uk}}}\] \(E\) je elektromotorni napon izvora struje.
Ukupan otpor kruga jednak je serijskom spoju unutarnjeg otpora \(R\) i dva otpora u krugu \(2\,R\) i \(3\,R\). \[R_{\textrm{uk}}=R+2\,R+3\,R=6\,R\] Krugom prolazi struja: \[I=\frac{E}{R_{\textrm{uk}}}=\frac{30}{6\,R}=\frac{5}{R}\] Napon na otporniku \(2\,R\) je: \[U_{2}=I\cdot 2\,R=\frac{5}{R}\cdot 2\,R=10\,\textrm{V}\]
10. zadatak
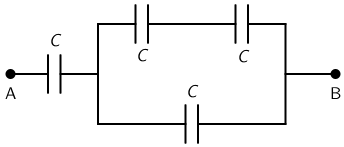
Četiri kondenzatora jednakih kapaciteta C = 5 μF spojena su kao na slici.
Koliko iznosi ukupan kapacitet ovako spojenih kondenzatora između točaka A i B?
- A. C = 3 μF
- B. C = 5 μF
- C. C = 5,3 μF
- D. C = 8,3 μF
Kapacitet serijski spojenih kondenzatora: \[\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}\] Kapacitet paralelno spojenih kondenzatora: \[C=C_{1}+C_{2}\]
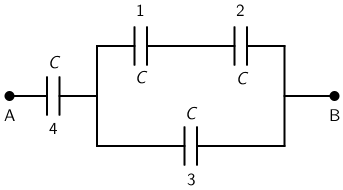
Kondenzatori 1 i 2 spojeni su serijski: \[\frac{1}{C_{12}}=\frac{1}{C}+\frac{1}{C}=\frac{2}{C}\] \[C_{12}=\frac{C}{2}\] \(C_{12}\) i 3 spojeni su paralelno: \[C_{123}=C_{12}+C=\frac{C}{2}+C=\frac{3\,C}{2}\] \(C_{123}\) i 4 spojeni su serijski: \[\frac{1}{C_{1234}}=\frac{1}{C_{123}}+\frac{1}{C}=\frac{2}{3\,C}+\frac{1}{C}=\frac{5}{3\,C}\] \[C_{1234}=\frac{3\,C}{5}=\frac{3\cdot 5}{5}=3\,\mu\textrm{F}\]
11. zadatak
Tri jednaka ravna magneta spojimo u jednu cjelinu, kao što je prikazano na slikama.
Koji crtež ispravno prikazuje razmještaj polova magneta nakon spajanja?

- A. Crtež A.
- B. Crtež B.
- C. Crtež C.
- D. Crtež D.
Ako razrežemo magnet po sredini dobit ćemo dva magneta s dva pola. Isto vrijedi i za spajanje magneta. Uvijek dobijemo magnete koji imaju dva pola, sjeverni (N) i južni (S).
Razmještaj polova magneta ispravno prikazuje crtež D.
12. zadatak
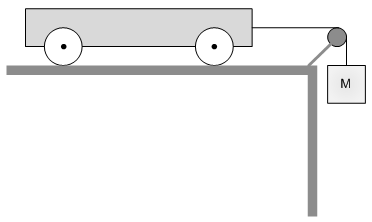
Učenici izvode pokus u kojem kolica početno miruju na stolu, a uteg je na najvišem položaju kako je prikazano na slici. Kolica se zatim gibaju po
ravnome horizontalnome stolu, dok uteg pričvršćen za njih preko koloture pada prema dolje. Učenici su izmjerili da se u nekome vremenskome intervalu
kinetička energija kolica povećala za 1,4 J, a kinetička energija utega za 0,3 J.
Za koliko se smanjila gravitacijska potencijalna energija utega u tom vremenskom intervalu ako je trenje zanemarivo?
- A. 0,3 J
- B. 1,1 J
- C. 1,4 J
- D. 1,7 J
Primijenite zakon očuvanja mehaničke energije. Koji se oblici mehaničke energije kolica i utega mijenjaju? Što iz toga možete zaključiti?
Potencijalna energija kolica se ne mijenja, nego samo kinetička. Kod utega mijenjaju se oba oblika energije. Kako ukupna mehanička energija mora ostati jednaka, zaključujemo da porast kinetičke energije kolica i utega uzrokuje smanjenje potencijalne energije utega: \[\Delta E_{\textrm{p}}=1,4+0,3=1,7\,\textrm{J}\]
13. zadatak
Njihalo preneseno sa Zemlje na Mjesec harmonijski titra periodom koji je 2,45 puta duži od perioda harmonijskoga titranja toga njihala na Zemlji.
Koliko iznosi ubrzanje slobodnoga pada na Mjesecu, ako je ubrzanje slobodnoga pada na Zemlji \(g\)?
- A. \(g/6\)
- B. \(g/2,45\)
- C. \(2,45\,g\)
- D. \(6\, g\)
Period titranja matematičkog njihala: \[T=2\,\pi\,\sqrt{\frac{\ell}{g}}\]
\[\frac{T_{\small\textrm{M}}}{T_{\small\textrm{Z}}}=2,45\] \[T_{\small{\textrm{M}}}=2\,\pi\,\sqrt{\frac{\ell}{g_{\small{\textrm{M}}}^{\,}}}\] \[T_{\small{\textrm{Z}}}=2\,\pi\,\sqrt{\frac{\ell}{g}}\] \[\frac{T_{\small{\textrm{M}}}}{T_{\small{\textrm{Z}}}}=2\,\pi\,\sqrt{\frac{\ell}{g_{\small{\textrm{M}}}^{\,}}}:2\,\pi\,\sqrt{\frac{\ell}{g}}\] \[\frac{T_{\small{\textrm{M}}}}{T_{\small{\textrm{Z}}}}=\sqrt{\frac{\ell\,g}{g_{\small{\textrm{M}}}^{\,}\,\ell}}\] \[\frac{T_{\small{\textrm{M}}}}{T_{\small{\textrm{Z}}}}=\sqrt{\frac{g}{g_{\small{\textrm{M}}}^{\,}}}=2,45\] \[\sqrt{\frac{g}{g_{\small{\textrm{M}}}^{\,}}}=2,45\] \[\frac{g}{g_{\small{\textrm{M}}}^{\,}}=2,45^{2}\] \[g_{\small{\textrm{M}}^{\,}}=\frac{g}{2,45^{2}}\] \[g_{\small{\textrm{M}}^{\,}}=\frac{g}{6}\]
14. zadatak
Uteg pričvršćen za oprugu leži na horizontalnoj podlozi i harmonijski titra u horizontalnoj ravnini. Trenje je zanemarivo. Ukupna energija utega pri maksimalnome otklonu od ravnotežnoga položaja iznosi 2 J.
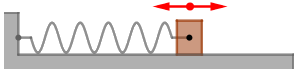
Koliko iznosi ukupna energija utega u trenutku kada on prolazi kroz ravnotežni položaj?
- A. 0 J
- B. 1 J
- C. 2 J
- D. 4 J
Primijenite zakon očuvanja energije. U kojem je obliku ukupna energija u krajnjim položajima utega? U kojem je obliku ukupna energija u ravnotežnom položaju?
Ukupna energija jednaka je zbroju kinetičke i potencijalne energije. U krajnjem položaju uteg zastane pa mu je kinetička energija jednaka nuli, a potencijalna je maksimalna. U ravnotežnom je položaju potencijalna energija jednaka nuli, jer opruga nije niti rastegnuta niti stisnuta, a kinetička je energija maksimalna. Prema zakonu očuvanja energije, ukupna je energija jednaka i u krajnjem i u ravnotežnom položaju pa je točan odgovor 2 J.
15. zadatak
Uteg mase \(m\) ovješen o oprugu konstante \(k\) titra periodom \(T\).
Kojim će periodom titrati uteg mase \(4\, m\) ovješen o istu oprugu?
- A. \(2\,T\)
- B. \(4\,T\)
- C. \(8\,T\)
- D. \(16\,T\)
Period titranja utega mase \(m\) ovješenog na oprugu konstante elastičnosti \(k\): \[T=2\,\pi\sqrt{\frac{m}{k}}\]
\[T=2\,\pi\sqrt{\frac{m}{k}}\] Period titranja proporcionalan je s \(\sqrt{m}\). Ako se masa utega poveća četiri puta, period tiranja povećat će se \(\sqrt{4}=2\) puta.
16. zadatak
Dvije konvergentne leće imaju žarišne daljine od 10 cm i 5 cm.
Na kojoj međusobnoj udaljenosti trebaju biti leće da paralelni snop svjetlosti, koji upada na prvu leću, izlazi kao paralelni snop iz druge leće?
- A. 15 cm
- B. 5 cm
- C. 10 cm
- D. 25 cm
Paralelan snop svjetlosti koji upada na konvergentnu leću lomi se tako da prolazi kroz njezino žarište.
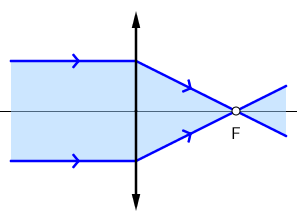
Paralelan snop svjetlosti koji izlazi iz prednjeg žarišta konvergentne leće lomi se tako da bude paralelan s optičkom osi.
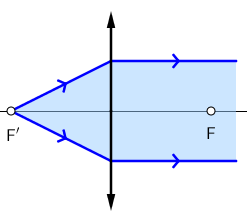
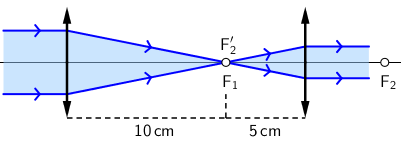
Glavno žarište prve leće F1 i prednje žarište druge leće F′2 moraju biti u istoj točki.
17. zadatak
Vrijeme poluraspada neke atomske jezgre iznosi 8 minuta.
Nakon 32 minute od početnoga broja N0 jezgara
raspadne se:
- A. \(\large{\frac{15}{16}}\normalsize{\,N_{0}\,\textrm{jezgara}}\)
- B. \(\large{\frac{1}{16}}\normalsize{\,N_{0}\,\textrm{jezgara}}\)
- C. \(\large{\frac{7}{8}}\normalsize{\,N_{0}\,\textrm{jezgara}}\)
- D. \(\large{\frac{1}{4}}\normalsize{\,N_{0}\,\textrm{jezgara}}\)
Zakon radioaktivnog raspada
\[N=N_{0}\cdot 2^{\mathbf{-}\large{\frac{t}{T}}}\]
\(N\)-broj neraspadnutih jezgara nakon vremena \(t\)
\(N_{0}\)-početni broj jezgara
\(T\)-vrijeme poluraspada
Broj jezgara koje su se raspale nakon vremena \(t\): \[\Delta N=N_{0}-N\] \[\Delta N=N_{0}-N_{0}\cdot 2^{\mathbf{-}\large{\frac{t}{T}}}\] \[\Delta N=N_{0}\,\left(1-2^{\mathbf{-}\,\large{\frac{t}{T}}}\right)\] \[\Delta N=\frac{15}{16}\,N_{0}\]
18. zadatak
Što nastaje pored kisika u reakciji: \[{_{\,\,7}^{14}}\,\textrm{N}+{_{2}^{4}}\,\alpha \rightarrow{_{\,\,8}^{17}}\,\textrm{O}+?\]
- A. neutron
- B. elektron
- C. pozitron
- D. proton
Alfa raspad: \[_{Z}^{A}\textrm{X}\rightarrow _{2}^{4}\textrm{He}+\,_{Z-2}^{A-4}\textrm{Y}\] Beta minus raspad: \[_{Z}^{A}\textrm{X}\rightarrow _{-1}^{\;\;0}\textrm{e}+\,_{Z+1}^{\;\;\;A}\textrm{Y}\] Beta plus raspad: \[_{Z}^{A}\textrm{X}\rightarrow _{+1}^{\;\;0}\textrm{e}+\,_{Z-1}^{\;\;\;A}\textrm{Y}\] Gama raspad: \[_{Z}^{A}\,\textrm{X}^{*}\rightarrow \gamma+\,_{Z}^{A}\textrm{X}\]
Alfa raspad: \[{_{\,\,7}^{14}}\,\textrm{N}+{_{2}^{4}}\,\alpha \rightarrow{_{\,\,8}^{17}}\,\textrm{O}+{_{1}^{1}}\,\textrm{p}\] Nastaje proton (jezgra atoma vodika)
19. zadatak
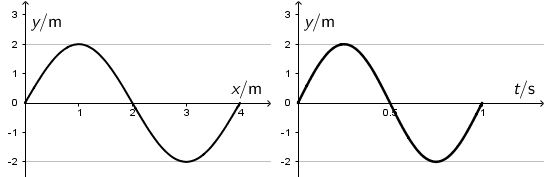
Graf 1 prikazuje ovisnost elongacije o položaju progresivnoga vala u nekome trenutku, a graf 2. prikazuje ovisnost elongacije o vremenu za isti val. Koliko iznosi valna duljina λ i period T toga vala?
- A. λ = 2 m i T = 0,5 s
- B. λ = 2 m i T = 1 s
- C. λ = 4 m i T = 0,5 s
- D. λ = 4 m i T = 1 s
Iz prvog grafa pročitamo valnu duljinu λ = 4 m, a iz drugog period titranja izvora vala T = 1 s.
20. zadatak
Koliko iznosi energija fotona valne duljine 750 nm?
- A. 1,65 eV
- B. 2,64 eV
- C. 3,65 eV
- D. 4,64 eV
Energija fotona: \[E_{\textrm{f}}=h\,f\] \[c=f\,\lambda\]
\[E_{\textrm{f}}=\frac{h\,c}{\lambda}=2,65\cdot 10^{-19}\,\textrm{J}\] \[1\,\textrm{eV}=1,6\cdot 10^{-19}\,\textrm{J}\] \[E_{\textrm{f}}=1,66\,\textrm{eV}\]
21. zadatak
U zamišljenome eksperimentu dva se svemirska broda A i B gibaju jednoliko pravocrtno u istome smjeru. Relativna brzina broda A u odnosu na brod B
iznosi 0,4 c, gdje \(c\) označava brzinu svjetlosti u vakuumu. Kapetan broda B pošalje laserski puls svjetlosti u smjeru gibanja
broda.
Koliko će iznositi brzina pulsa mjerena iz broda A?
- A. 0,4 c
- B. 0, c
- C. c
- D. 1,4 c
Brzina svjetlosti u svim inercijskim sustavima je konstantna i u vakuumu iznosi približno \(c=3\cdot 10^{8}\,\textrm{m}/\textrm{s}.\)
Brzina svjetlosti u svim inercijskim sustavima je konstantna. Točan odgovor je C.
22. zadatak
Imamo dvije jednake kuglice na istoj visini od tla. Prvu samo ispustimo, dok drugu bacimo vodoravno. Vrijeme nakon kojega prva kuglica padne na tlo
označimo s \(t_{1}\), a vrijeme nakon kojega padne druga kuglica označimo s \(t_{2}\).
Kako će se odnositi vremena \(t_{1}\) i \(t_{2}\)?
- A. \(t_{1} \lt t_{2}\)
- B. \(t_{1} = t_{2}\)
- C. \(t_{1} \gt t_{2}\)
Tijelo koje slobodno pada s visine \(h\) past će na tlo nakon vremena: \[t=\sqrt{\frac{2\,h}{g}}\] Tijelo koje je s iste visine izbačeno u vodoravnom smjeru izvodi složeno gibanje koje se sastoji od jednolikog gibanja po vodoravnom pravcu brzinom kojom je izbačeno i od slobodnog pada u vertikalnom smjeru
Tijelo će se u svakom trenutku naći na onom mjestu do kojega bi stiglo kada bi istodobno izvodilo oba složena gibanja. Zbog toga će vrijeme za koje će tijelo pasti na tlo biti jednako kao kod slobodnog pada.
\[t_{1} = t_{2}\] Točan odgovor je B.
23. zadatak
De Broglieva valna duljina nekoga elektrona jednaka je valnoj duljini nekoga fotona. Iz toga slijedi da je količina gibanja fotona:
- A. manja nego količina gibanja elektrona
- B. veća nego količina gibanja elektrona
- C. jednaka količini gibanja elektrona
De Broglieva valna duljina čestice mase \(m\) koja se giba brzinom \(v\): \[\lambda=\frac{h}{m\,v}\] U nazivniku je količina gibanja čestice: \[p=m\,v\] Zato de Broglievu valnu duljinu možemo prikazati i kao: \[\lambda=\frac{h}{p}\]
De Broglieva valna duljina fotona: \[\lambda_{\textrm{f}}^{\,}=\frac{h}{m\,c}=\frac{h}{p_{\textrm{f}}^{\,}}\] De Broglieva valna duljina elektrona: \[\lambda_{\textrm{e}}^{\,}=\frac{h}{m\,v}=\frac{h}{p_{\textrm{e}}^{\,}}\]
\[\lambda_{\textrm{f}}^{\,}=\lambda_{\textrm{e}}^{\,} \Rightarrow p_{\textrm{f}}^{\,}=p_{\textrm{e}}^{\,}\]
24. zadatak
Unutrašnja energija idealnoga plina iznosi \(U_{0}\). Plin podvrgnemo izotermnoj promjeni stanja.
Nakon toga će iznos unutrašnje energije plina biti:
- A. manji od \(U_{0}\)
- B. jednak \(U_{0}\)
- C. veći od \(U_{0}\)
U modelu idealnog plina zanemarujemo potencijalnu energiju molekula. Zato je unutarnja energija idealnog plina jednaka srednjoj kinetičkoj energiji svih molekula plina. \[U=N\cdot \bar{E}_{\textrm{k}}\] Srednja kinetička energija molekula jednoatomnog idealnog plina je: \[\bar{E}_{\textrm{k}}=\frac{3}{2}\,k\,T\] Srednja kinetička energija molekula dvoatomnog idealnog plina je: \[\bar{E}_{\textrm{k}}=\frac{5}{2}\,k\,T\]
Unutarnja energija jednoatomnog idealnog plina: \[U=\frac{3}{2}\,N\,k\,T\] U izotermnom procesu temperatura je konstantna. Zato se unutarnja energija ne mijenja. Točan odgovor je B.
25. zadatak
Ljuljajući se na ljuljački Hana prođe kroz najnižu točku putanje brzinom 2 m/s. Trenje je zanemarivo.
Kolika je visina s koje se Hana spustila, mjereno u odnosu na najnižu točku putanje?
Odgovor: m
Primijenite zakon očuvanja energije. U kojemu je obliku energija u najvišoj točki, a u kojemu u najnižoj točki?
Ukupna energija u najvišoj točki jednaka je potencijalnoj energiji, jer je kinetička energija jednaka nuli: \[E_{1}=E_{\textrm{k}}+E_{\textrm{p}}=0+E_{\textrm{p}}=m\,g\,h\] Ukupna energija u najnižoj točki jednaka je kinetičkoj energiji, jer je potencijalna energija jednaka nuli: \[E_{2}=E_{\textrm{k}}+E_{\textrm{p}}=E_{\textrm{k}}+0=\frac{1}{2}m\,v^{2}\] Prema zakonu očuvanja energije, ove su dvije energije jednake: \[E_{1}=E_{2}\Rightarrow E_{\textrm{p}}=E_{\textrm{k}}\Rightarrow m\,g\,h=\frac{1}{2}m\,v^{2}\] Iz posljednje jednadžbe za visinu dobijemo: \[h=\frac{v^{2}}{2\,g}=0,2\,\textrm{m}\]
26. zadatak
Kolica mase 0,4 kg gibaju se brzinom 2 m/s. Njima ususret gibaju se druga kolica mase 0,25 kg.
Koliko treba iznositi brzina drugih kolica da nakon sudara oboja kolica miruju?
Odgovor: m/s
Primijenite zakon očuvanja količine gibanja. Kolika je ukupna količina gibanja nakon sudara? Kolika mora biti ukupna količina gibanja prije sudara?
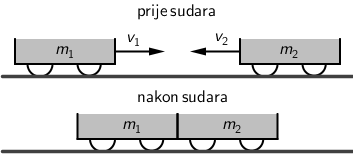
Ukupna količina gibanja nakon sudara je nula, pa i prije sudara mora biti jednaka nuli: \[m_{1}\,v_{1}−m_{2}\,v_{2}=0\] Iz ove jednadžbe dobijemo brzinu drugih kolica: \[v_{2}=\frac{m_{1}\,v_{1}}{m_{2}}=\frac{0,4\cdot 2}{0,25}=3,2\,\textrm{m}/\textrm{s}\]
27. zadatak
1. Pretvorite temperaturu od \(37\,^{o}\textrm{C}\) u kelvine.
Odgovor: K
2. Temperatura tijela povisila se od \(37\,^{o}\textrm{C}\) na \(39\,^{o}\textrm{C}\).
Koliki je porast temperature u kelvinima?
Odgovor: K
- \(37\,^{0}\textrm{C}=37+273=310\,\textrm{K}\)
- \(\Delta t=2\,^{0}\textrm{C}\Rightarrow \Delta t=2\,\textrm{K}\)
28. zadatak
Marko, Ivan i Dominik raspravljaju o računu koji im je poslala Hrvatska elektroprivreda.
Marko: "Kilovatsati … to nam govori koliko smo struje potrošili ovog mjeseca."
Ivan: "Ne, kilovatsati su jedinica za električni naboj koji smo potrošili."
Dominik: "Moram vas obojicu ispraviti, radi se zapravo o električnoj snazi koju smo potrošili."
Tko je u pravu: Marko, Ivan, Dominik ili nitko?
Odgovor:
Ukupan otpor u krugu izmjenične struje (impedancija) u kojemu su serijski spojeni zavojnica, kondenzator i otpornik: \[Z=\sqrt{R^{2}+\left(R_{\small{\textrm{L}}}-R_{\small{\textrm{C}}}\right)^{2}}\]
Kilovatsat (oznaka kWh) je jedinica za energiju. \[P=\frac{E}{t}\Rightarrow E=P\,t\]
29. zadatak
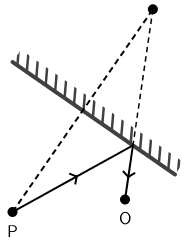
Slika prikazuje predmet P i ravno zrcalo.
Hoće li opažač, čiji je položaj oka naznačen točkom O, vidjeti sliku predmeta u zrcalu? Naznačite na slici put svjetlosti od predmeta do
opažača kao obrazloženje svojega odgovora.
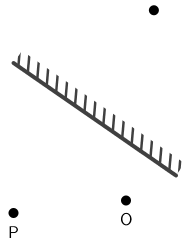
Odgovor: (upišite hoće ili neće)
Period LC kruga odredimo pomoću frekvencije: \[T=\frac{1}{f}\] Period LC kruga ovisi o induktivitetu zavojnice \(L\) i kapacitetu kondenzatora \(C\): \[T=2\,\pi\,\sqrt{L\,C}\] To je Thomsonova formula koju možete pronaći u knjižici s formulama.
30. zadatak
Grijaća ploča na štednjaku je kružnoga oblika polumjera 10 cm. U ploču je ugrađen grijač
snage 1,2 kW.
Kolika je temperatura površine uključene grijaće ploče ako ploča zrači kao crno tijelo?
Odgovor: K
- \(P\)-snaga zračenja apsolutno crnog tijela
- \(\sigma\)-Stefan-Boltzmannova konstanta
- \(S\)-površina crnog tijela
- \(T\)-temperatura crnog tijela u kelvinima
\[P=\sigma\,S\,T^{4}\] \[T=\sqrt[4]{\frac{P}{\sigma\,S}}\] \[T=\sqrt[4]{\frac{1200}{5,67\cdot 10^{-8}\cdot 10^{-2}\pi}}=906\,\textrm{K}\]
31. zadatak
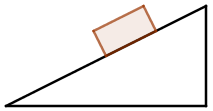
Tijelo klizi niz kosinu nagiba 45° bez trenja.
1. Nacrtajte sve sile koje djeluju na tijelo.
2. Izračunajte ubrzanje tijela.
Odgovor: \(\textrm{m}/\textrm{s}^{2}\)
Na tijelo djeluje sila teža \(F_{\textrm{g}}\) vertikalno prema dolje i reakcija podloge \(N\) okomito na kosinu.
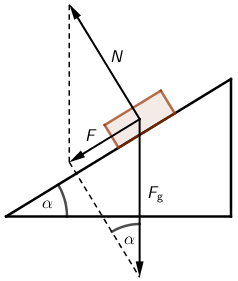
Rezultantna sila \(F\) ubrzava tijelo prema dnu kosine. Trenje je zanemareno. \[F=F_{\textrm{g}}\,\textrm{sin}\,\alpha=m\,g\,\textrm{sin}\,\alpha\] Akceleraciju tijela odredimo primjenom temeljnog zakona gibanja: \[a=\frac{m\,g\,\textrm{sin}\,\alpha}{m}=g\,\textrm{sin}\,\alpha\] \[a=g\,\textrm{sin}\,\alpha=7,1\,\textrm{m}/\textrm{s}^{2}\]
32. zadatak
Idealni plin prolazi kružni proces (A → B → C → A) prikazan na slici.
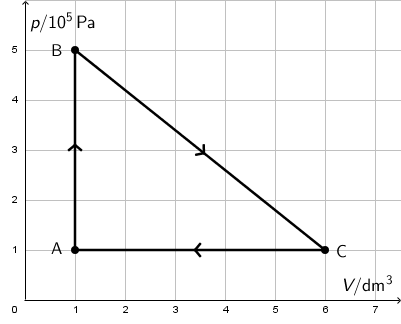
1. Na kojem se dijelu kružnoga procesa ne vrši rad?
- A. A → B.
- B. B → C.
- C. C → A.
2. Za koliko se promijeni unutarnja energija plina pri ovome kružnome procesu?
Odgovor: J
3. Izračunajte izvršeni rad.
Odgovor: J
- Koliki rad obavi olih pri izohornom procesu?
- Kolika je promjena unutarnje energije plina u kružnom procesu?
- Kako grafički iz \(p,V\) grafa određujemo rad plina?
- Pri izohornom procesu volumen plina je konstantan: \[\Delta V=0\] pa plin ne obavlja rad
- Konačno stanje plina u kružnom procesu jednako je početnom: \[p_{\textrm{kon}}=p_{\textrm{poč}}; V_{\textrm{kon}}=V_{\textrm{poč}};T_{\textrm{kon}}=T_{\textrm{poč}}\] pa je i unutarnja energija jednaka: \[U_{\textrm{kon}}=U_{\textrm{poč}} \Rightarrow \Delta U=0\]
- Rad kojega obavi plin u kružnom procesu jednak je, u ovom slučaju, površini trokuta: \[W=\frac{\left(p_{\small{\textrm{B}}}-p_{\small{\textrm{A}}}\right)\cdot \left(V_{\small{\textrm{C}}}-V_{\small{\textrm{A}}}\right)}{2}\] \[W=\frac{4\cdot 10^{5}\cdot 5 \cdot 10^{-3}}{2}=\frac{2000}{2}=1000\,\textrm{J}\]
33. zadatak
U magnetsko polje \(B\) uleti proton brzinom \(v\) okomito na silnice polja te se u polju nastavi gibati po kružnoj stazi polumjera \(5\,\textrm{cm}.\)
Koliki bi bio polumjer staze po kojem bi se u istome polju gibala \(\alpha-\textrm{čestica}\) jednakom brzinom?
(Masa alfa-čestice je 4 puta veća od mase protona, a naboj joj je dva puta veći od naboja protona.)
Odgovor: cm
Na nabijenu česticu koja se giba u magnetskom djeluje Lorentzova sila: \[F_{\small{\textrm{L}}}=q\,v\,B\,\textrm{sin}\,\alpha\] Ako se čestica giba okomito na smjer magnetskog polja kut između smjera brzine i smjera magnetskog polja je \(90\,^{0}\) pa je Lorentzova sila: \[F_{\small{\textrm{L}}}=q\,v\,B\]
Lorentzova je sila u svakoj točki putanje okomita na vektore \(\vec{v}\) i \(\vec{B}\), a to znači da je usmjerena prema istoj točki. Zbog toga će se čestica gibati jednoliko po kružnici. Prema tome, Lorentzova će sila imati ulogu centripetalne sile. Odredimo polumjer kružnice po kojoj se nabijena čestica giba. \begin{matrix} \begin{align*} &F_{\small{\textrm{L}}}=F_{\small{\textrm{C}}}\\ &q\,v\,B=\frac{m\,v^{2}}{r}\\ &q\,B=\frac{m\,v}{r} \end{align*} \end{matrix} Polumjer kružnice po kojoj se nabijena čestica giba u magnetskom polju jednak je: \[r=\frac{m\,v}{q\,B}\]
Proton se u magnetskom polju giba po kružnici polumjera: \[r=\frac{m\,v}{e\,B}\] Alfa čestica gibala bi se po kružnici polumjera: \[r_{\alpha}=\frac{4\,m\,v}{2\,e\,B}=2\,\frac{m\,v}{e\,B}=2\,r=10\,\textrm{cm}\]
34. zadatak
Optička rešetka ima 400 pukotina na svaki milimetar duljine. Rešetku obasjavamo svjetlošću valne duljine 500 nm.
1. Koliki je najveći red spektra moguće dobiti tom optičkom rešetkom?
Odgovor =
2. Koliko ukupno maksimuma daje ta rešetka?
Odgovor =
Prisjetite se uvjeta za maksimume na optičkoj rešetci. Koliki je najveći kut pod kojim možemo vidjeti maksimum?
Odredimo konstantu optičke rešetke: \[d=\frac{1}{400}=0,0025\,\textrm{mm}=2,5\cdot 10^{−6}\textrm{m}\] Kutevi pod kojima vidimo maksimume određeni su jednadžbom: \[d\,\textrm{sin}\,\alpha=k\,\lambda\] Napišimo ovu jednadžbu u obliku: \[k\,\lambda\,d=\textrm{sin}\,alpha\] Kut \(\alpha\) može biti manji ili jednak 90 stupnjeva: \[\alpha \leq 90^{0} \Rightarrow \textrm{sin}\,\alpha \leq 1\] Za maksimalni \(k\) dobijemo: \[k_{\textrm{maks}} \leq d\,\lambda\] Uvrštavanjem dobijemo da je \(k = 5\) Ukupan broj maksimuma je: \[2\,k_{\textrm{maks}}+1=11\] (Pet maksimuma iznad centralnog, 5 maksimuma ispod centralnog i centralni.)
35. zadatak
Rabeći fotoelektrični učinak moguće je odrediti izlazni rad za određeni materijal mjerenjem frekvencije upadnoga zračenja i maksimalne kinetičke energije
fotoelektrona.
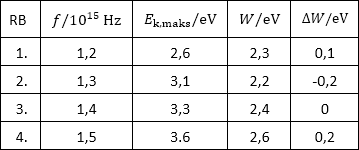
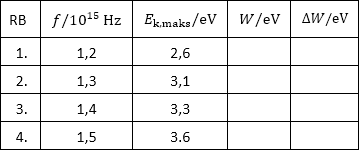
Tablica prikazuje rezultate nekoliko mjerenja frekvencije i maksimalne kinetičke energije fotoelektrona.
Dopunite tablicu i odredite srednju vrijednost izlaznoga rada te pripadnu maksimalnu apsolutnu pogrješku.
\(\overline{W}\) = eV
\(\left|\Delta W\right|\) = eV
Srednja vrijednost
Srednja vrijednost jednaka je aritmetičkoj sredini kada smo izvršili nekoliko mjerenja neke fizičke veličine \(x\). Broj mjerenja označimo s \(n\):
\[\overline{x}=\frac{x_{1}+x_{2}+x_{3}\,+...+\,x_{n}}{n}\]
Maksimalna apsolutna pogreška
Odredimo odstupanja svakog pojedinog mjerenja od srednje vrijednosti:
\[\Delta x_{\textrm{i}}=x_{\textrm{i}}-\overline{x}\]
Iz ovako dobivenih odstupanja uzimamo ono koje je po apsolutnom iznosu najveće i to nazivamo maksimalnom apsolutnom pogreškom: \(\left|\Delta x\right|.\)
Zapis rezultata mjerenja
\[x=\left(\overline{x}\pm \left|\Delta x\right|\right)\,\left[\textrm{odgovarajuća jedinica}\right]\]
Izlazni rad izračunamo iz Einsteinove jednadžbe fotoelektričnog učinka: \[E_{\textrm{f}}=W+E_{\textrm{k,maks}}\] \[W=E_{\textrm{f}}-E_{\textrm{k,maks}}\] \[W=h\,f-E_{\textrm{k,maks}}\] Kinetička energija izmjerena je u eV. Pretvorimo i energiju fotona u eV: 1 eV = 1,6·10-19 J \[E_{\textrm{f}}=h\,f=\frac{6,63\cdot 10^{-34}}{1,6\cdot 10^{-19}}\,f\] \[E_{\textrm{f}}/\textrm{eV}=4,1\cdot 10^{-15}\,f\] Izlazni rad: \[W/\textrm{eV}=4,1\cdot 10^{-15}\,f-E_{\textrm{k,maks}}\] Rezultate dobivene računom moramo prikazati s omoliko decimalnih mjesta koliko imaju i podaci dobiveni mjerenjem. \[W_{1}=2,3\,\textrm{eV}\] \[W_{2}=2,2\,\textrm{eV}\] \[W_{3}=2,4\,\textrm{eV}\] \[W_{4}=2,6\,\textrm{eV}\] Ove podatke upišemo u četvrti stupac tablice.
Srednja vrijednost izlaznog rada jednaka je aritmetičkoj sredini podataka iz četvrtog stupca tablice. \[\overline{W}=\frac{W_{1}+W_{2}+W_{3}+W_{4}}{4}\] \[\overline{W}=\frac{2,3+2,2+2,4+2,6}{4}=2,4\,\textrm{eV}\]
Izračunajmo odstupanja između srednje vrijednosti i podataka iz četvrtog stupca tablice: \[\Delta W_{1}=\overline{W}-W_{1}=0,1\,\textrm{eV}\] \[\Delta W_{2}=\overline{W}-W_{2}=-0,2\,\textrm{eV}\] \[\Delta W_{3}=\overline{W}-W_{3}=0\,\textrm{eV}\] \[\Delta W_{4}=\overline{W}-W_{4}=0,2\,\textrm{eV}\]
Najveće odstupanje po apsolutnoj vrijednosti je maksimalna apsolutna pogreška: \[\left|\Delta W\right|=0,2\,\textrm{eV}\]