Ljetni rok 2012. godine
1. zadatak
Crtež prikazuje grafove položaja u ovisnosti o vremenu za četiri tijela.
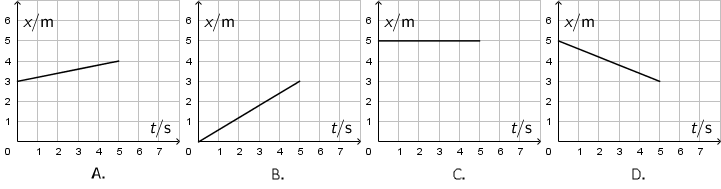
Koje tijelo ima najveću brzinu t = 1 s?
- A. Graf A.
- B. Graf B.
- C. Graf C.
- D. Graf D.
Kako iz \(x,t\) grafa određujemo brzinu?
Sva četiri grafa prikazuju jednoliko gibanje, što znači da je brzina u bilo kojem trenutku konstantna. Iz grafa položaja brzinu određujemo kao nagib pravca. Najveći je nagib pravca na grafu B, pa je i brzina najveća.
2. zadatak
Materijalna točka giba se jednoliko po kružnici.
Što od navedenoga vrijedi za vektor količine gibanja te točke?
- A. Ne mijenja se.
- B. Mijenja se po iznosu, ali ne mijenja smjer.
- C. Mijenja se po smjeru, ali ne mijenja iznos.
- D. Mijenja se i po iznosu i po smjeru.
Vektor količine gibanja: \[\vec{p}=m\,\vec{v}\]
Vektor količine gibanja ima jednak smjer i orijentaciju kao i vektor brzine. Kod jednolikog gibanja po kružnici mijenja se smjer brzine, a iznos ne. Isto vrijedi i za količinu gibanja. Točan odgovor je C.
3. zadatak
Dvije točkaste mase udaljene su za r. Mase se privlače gravitacijskom silom F.
Kolika treba biti udaljenost između njih da se privlače silom F/4?
- A. r/4
- B. r/2
- C. 2 r
- D. 4 r
Opći zakon gravitacije: \[F=G\,\frac{m_{1}\,m_{2}}{r^{2}}\]
Gravitacijska sila obrnuto razmjerna je kvadratu udaljenosti između tijela koja se privlače. Ako se sila četiri puta smanji, znači da se udaljenost povećala dva puta.
4. zadatak
Filip pliva s jedne na drugu obalu rijeke brzinom od 0,5 m/s u smjeru okomitom na tok rijeke.
Rijeka je široka 10 m.
Koliko ga je metara rijeka odvukla nizvodno ako je brzina rijeke 3 m/s?
- A. 10 m
- B. 15 m
- C. 30 m
- D. 60 m
Složeno gibanje sastoji se od dva ili više neovisnih gibanja koja koja se odvijaju istodobno.
U zadatku Filipovo je gibanje složeno i sastoji se od jednolikog gibanja (plivanja) okomito na tok rijeke i gibanja rijeke.
Plivač izvodi složeno gibanje koje se sastoji od jednolikog gibanja plivača u okomitom smjer na tok rijeke brzinom \(v_{\textrm{p}}\) i jednolikog gibanja rijeke brzinom \(v_{\textrm{r}}\). Zbog toga će plivač iz točke O stići u točku C, gibajući se brzinom \(v\) za neko vrijeme \(t\).
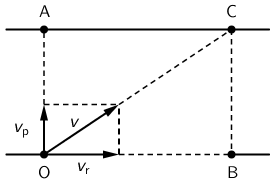
Kada bi brzina rijeke bila jednaka nuli, plivač bi iz točke O došao u točku A za vrijeme \(t\). \[d_{\small{\textrm{OA}}}=v_{\textrm{p}}\cdot t\] Kada bi brzina plivača bila jednaka nuli, za isto vrijeme \(t\) rijeka bi ga odnijela u točku B. \[d_{\small{\textrm{OB}}}=v_{\textrm{r}}\cdot t\] Iz prve jednadžbe odredimo vrijeme t: \[t=d_{\small{\textrm{OA}}}/v_{\textrm{p}}=20\,\textrm{s}\] Iz druge jednadžbe odredimo za koliko ga je rijeka odvukla nizvodno: \[d_{\small{\textrm{OB}}}=60\,\textrm{m}\]
5. zadatak
Kuglica u vodi tone, a ako je uronimo u tekućinu X ona lebdi kako je prikazano na crtežu.
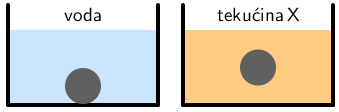
Koja je od navedenih tvrdnji točna?
- A. Gustoća tekućine X manja je od gustoće vode.
- B. Gustoća tekućine X veća je od gustoće vode.
- C. Gustoća kuglice manja je od gustoće tekućine X.
- D. Gustoća kuglice veća je od gustoće tekućine X.
Tijelo uronjeno u fluid će:
- tonuti, ako je gustoća tijela veća od gustoće fluida
- lebdjeti, ako je gustoća tijela jednaka gustoći fluida
- izroniti, ako je gustoća tijela manja od gustoće fluida
Tijelo u vodi: \[\rho_{\textrm{tijelo}} > \rho_{\textrm{voda}}\qquad(1)\] Tijelo u tekućini X: \[\rho_{\textrm{tijelo}} = \rho_{\small{\textrm{X}}}\qquad(2)\] Iz izraza (1) i (2) zaključujemo: \[\rho_{\small{\textrm{X}}} > \rho_{\textrm{voda}}\]
6. zadatak
Na vodoravnom stolu leži knjiga mase 4 kg. Vertikalno prema dolje na knjigu djelujemo silom iznosa 30 N.
Kolikom silom površina stola djeluje na knjigu?
- A. 0 N
- B. 30 N
- C. 40 N
- D. 70 N
Primijenite treći Newtonov zakon.
Na knjigu vertikalno prema dolje djeluju sila teža \(F_{\textrm{g}}=m\,g=40\,\textrm{N}\) i dodatna sila od \(30\,\textrm{N}\). Ukupna sila koja
djeluje na stol je \(40 + 30 = 70\,\textrm{N}\). Budući da knjiga miruje, rezultantna sila jednaka je nuli i zaključujemo da stol djeluje na knjigu
vertikalno prema gore silom od \(70\,\textrm{N}\).
Napomena
Za objašnjenje mogli smo koristiti i treći Newtonov zakon.
7. zadatak
Idealni plin prolazi kružni proces. Na crtežu je prikazano kako se pritom mijenja tlak plina \(p\) u ovisnosti o njegovom volumenu \(V\).
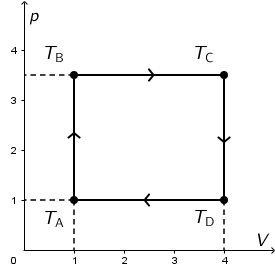
Koja od označenih temperatura ovog procesa je najniža?
- A. \(T_{\textrm{A}}\)
- B. \(T_{\textrm{B}}\)
- C. \(T_{\textrm{C}}\)
- D. \(T_{\textrm{D}}\)
Pomoć potražite na poveznici Jednadžba stanja plina.
Opća plinska jednadžba: \[\frac{p\,V}{T}=\textrm{konst.}\] Iz grafa vidimo da temperaturi \(T_\textrm{A}\) odgovaraju najniže vrijednosti tlaka i volumena pa je brojnik \(p\cdot V\) najmanji u odnosu na preostale tri temperature. Budući da je vrijednost razlomka konstantna, mora i temperatura \(T_\textrm{A}\), koja se nalazi u nazivniku, biti najmanja.
8. zadatak
Temperatura jednoatomnog idealnog plina iznosi T.
Što će se dogoditi s unutarnjom energijom jednoatomnog idealnog plina ako temperatura plina smanji na
T/2?
- A. Povećat će se dva puta.
- B. Smanjit će se dva puta.
- C. Povećat će se četiri puta.
- D. Smanjit će se četiri puta.
Srednja kinetička energija molekula jednoatomnog idealnog plina jednaka je: \[\overline{E}_{\textrm{k}}=\frac{3}{2}\,k\,T\] Potencijalnu energiju idealnog plina zanemarujemo pa je unutarnja energija jednaka srednjoj kinetičkoj energiji svih molekula. Označimo broj molekula s \(N\): \[U=N\,\overline{E}_{\textrm{k}}=\frac{3}{2}\,N\,k\,T\]
Unutarnju energiju jednoatomnog idealnog plina možemo prikazati kao: \[U=\frac{3}{2}\,N\,k\,T\] Vidimo da je unutarnja energija proporcionalna apsolutnoj temperaturi. Ako se temperatura smanji dva puta, i unutarnja energija smanjiti će se dva puta.
9. zadatak
Crtež prikazuje tri nabijene šuplje kugle od kojih su najmanje dvije negativno nabijene. Strjelice pokazuju smjer električnih sila koje djeluju na kugle.
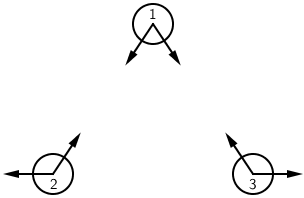
Koja je kugla pozitivno nabijena?
- A. kugla 1
- B. kugla 2
- C. kugla 3
- D. nijedna od njih
Pomoć potražite na poveznici Električna sila
Negativno nabijene kugle su 2 i 3 jer se jedino one međusobno odbijaju. Kugla 1 privlači kugle 2 i 3 pa je ona pozitivno nabijena.
10. zadatak
Koji graf prikazuje iznos električnog polja u ovisnosti o udaljenosti \(r\) od točkastog naboja?
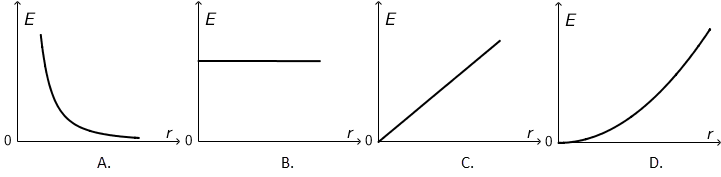
- A. graf A.
- B. graf B.
- C. graf C.
- D. graf D.
Pomoć potražite na poveznici Električno polje točkastog naboja, sfere i kugle.
Iznos električnog polja točkastog naboja: \[E=k\,\frac{q}{r^{2}}\] Na malim udaljenostima polje je veliko, a na velikim jako malo. Takvu ovisnost ispravno opisuje jedino graf A.
11. zadatak
Graf prikazuje napon između ploča kondenzatora u ovisnosti o naboju pri nabijanju kondenzatora.
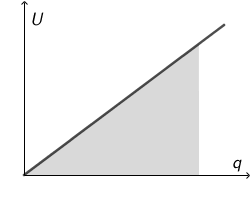
Koja je od navedenih tvrdnji točna?
- A. Nagib grafa jednak je kapacitetu kondenzatora.
- B. Označena površina ispod grafa jednaka je kapacitetu kondenzatora.
- C. Nagib grafa jednak je energiji pohranjenoj u kondenzatoru.
- D. Označena površina ispod grafa jednaka je energiji pohranjenoj u kondenzatoru.
Pomoć potražite na poveznici Električna potencijalna energija pločastog kondenzatora.
Označena površina na grafu jednaka je (površina trokuta): \[\textrm{Površina}=\frac{1}{2}q\,U\qquad(1)\] Naboj na pločama kondenzatora jednak je: \[q=C\,U\qquad(2)\] Uvrstimo izraz (2) u izraz (1): \[\textrm{Površina}=\frac{1}{2}C\,U^{2}\] Dobiveni izraz jednak je energiji kondenzatora: \[W=\frac{1}{2}C\,U^{2}\]
12. zadatak
Proton prolazi dijelom prostora u kojem na njega djeluje homogeno magnetsko polje.
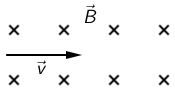
Koja strjelica prikazuje smjer sile na proton u trenutku prikazanom na crtežu?
- A. \(\large\uparrow\)
- B. \(\large\rightarrow\)
- C. \(\large\downarrow\)
- D. \(\large\leftarrow\)
Pomoć potražite na poveznici Lorentzova sila.
Primijenimo pravilo desnog dlana: Palac desne ruke postavimo u smjer gibanja naboja a ispružene prste usmjerimo u smjer magnetskog polja. Sila je okomita na dlan i djeluje iz dlana.
13. zadatak
Kroz zavojnicu prolazi izmjenična struja.
Kako se promijeni induktivni otpor zavojnice ako se period izmjenične struje poveća tri puta?
- A. Poveća se 3 puta.
- B. Smanji se 3 puta.
- C. Poveća se \(\sqrt{3}\).
- D. Smanji se \(\sqrt{3}\).
Pomoć potražite na poveznici Induktivni otpor.
Induktivni otpor može se prikazati kao: \[R_{\small{\textrm{L}}}=L\,\large\omega=\normalsize L\cdot\frac{2\,\pi}{T}\] Vidimo da je induktivni otpor obrnuto proporcionalan periodu izmjenične struje pa će se smanjiti tri puta.
14. zadatak
Jednostavno njihalo titra harmonijski.
Što treba učiniti da se poveća njegov period?
- A. smanjiti duljinu njihala
- B. povećati duljinu njihala
- C. smanjiti amplitudu titranja
- D. povećati amplitudu titranja
Pomoć potražite na poveznici Period matematičkog njihala.
Period titranja matematičkog njihala: \[T=2\,\pi\,\sqrt{\frac{\ell}{g}}\] Vidimo da je period proporcionalan sa \(\sqrt\ell\) pa će se povećanjem duljine njihala povećati i njegov period.
15. zadatak
Tijelo harmonijski titra amplitudom 2 cm.
Koliki put prijeđe tijekom dvaju perioda?
- A. 4 cm.
- B. 8 cm.
- C. 16 cm.
- D. 32 cm.
Ako se elongacija kod harmonijskog titranja mijenja kao: \[y=y_{0}\,\textrm{sin}\,\omega\, t\] onda se brzina mijenja kao: \[v=v_{0}\,\textrm{cos}\,\omega\, t\] Više o nastanku vala na užetu potražite na poveznici Nastanak transverzalnog vala.
Za vrijeme jednog perioda tijelo prijeđe put od O do A, od A do O, od O do B i od B do O.
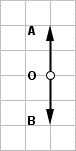
Dakle, tijelo prijeđe put koji je četiri puta veći od amplitude: 4·2 = 8 cm. Za dva perioda prijeći će dva puta veći put: 16 cm.
16. zadatak
Svjetlost frekvencije f i brzine c giba se kroz zrak i ulazi u sredstvo indeksa loma 1,3.
Koja je od navedenih tvrdnji točna za frekvenciju i brzinu svjetlosti u tom sredstvu?
- A. Frekvencija je f, a brzina 1,3 c.
- B. Frekvencija je f /1,3, a brzina c.
- C. Frekvencija je 1,3 f, a brzina c.
- D. Frekvencija je f, a brzina c/1,3.
Pomoć potražite na poveznici Lom svjetlosti.
Kada val prelazi iz jednog sredstva u drugo, mijenja se njegova brzina, prema tome i njegova valna duljina, dok frekvencija ostaje ista.
Apsolutni indeks loma sredstva definiran je kao \(n=c/v\). Brzina svjetlosti u vakuumu označena je sa \(c\), a u sredstvu sa \(v\).
Za brzinu svjetlosti u sredstvu dobijemo \(v=c/n= c/1,33.\)
Zaključak: frekvencija ostaje ista, a brzina je \(c/1,33.\)
17. zadatak
U medicinskoj dijagnostici koristi se ultrazvuk valne duljine 0,5 mm i brzine 1500 m/s.
Kolika je frekvencija tog ultrazvuka?
- A. 3,0·105 Hz
- B. 7,5·105 Hz
- C. 3,0·106 Hz
- D. 7,5·106 Hz
Pomoć potražite na poveznici Pretvorbe energije pri harmonijskom titranju.
Brzina širenja vala: \[v=\frac{\lambda}{T}\] Frekvencija titranja izvora vala: \[f=\frac{1}{T}\] Prema tome, brzinu možemo prikazati i kao: \[v=f\,\lambda\] Frekvencija je jednaka: \[f=\frac{v}{\lambda}=3\cdot 10^{6}\,\textrm{Hz}\]
18. zadatak
Čestice X i Y gibaju se brzinama istog iznosa. Čestica Y ima veću de Broglievu valnu duljinu od čestice X.
Koja je od navedenih tvrdnji točna?
- A. Y mora imati veći naboj nego X.
- B. Y mora imati manji naboj nego X.
- C. Y mora imati veću masu nego X.
- D. Y mora imati manju masu nego X.
Pomoć potražite na poveznici De Broglieva valna duljina.
De Broglieva valna duljina za neku česticu može se prikazati kao: \[\lambda=\frac{h}{m\,v}\] \[m=\frac{h}{\lambda\,v}\] Budući da su brzine kojima se gibaju obje čestice jednake, čestica koja ima veću de Broglievu valnu duljinu (Y) imat će manju masu.
19. zadatak
Masa \(\alpha\) čestice je \(6,645\cdot 10^{-27}\,\textrm{kg}\), a ukupna masa dvaju protona i dvaju neutrona \(6,695\cdot 10^{-27}\,\textrm{kg}\).
Kolika se energija oslobodi kod stvaranja \(\alpha\) čestice?
- A. 2,813 MeV
- B. 28,13 MeV
- C. 281,3 MeV
- D. 2813 MeV
Pomoć potražite na poveznici Nuklearne reakcije.
Energiju koja se oslobodi u nuklearnim reakcijama možemo izračunati kao: \[E=\Delta m\cdot c^{2}\] Ovdje je \(\Delta m\) razlika u masama čestica prije i poslije reakcije. \[\Delta m=6,695\cdot 10^{-27}-6,645\cdot 10^{-27}=5\cdot 10^{-29}\, \textrm{kg}\] Ovoj razlici masa odgovara energija: \[E=\Delta m\cdot c^{2}=4,5\cdot 10^{-12}\,\textrm{J}\] Ako to pretvorimo u MeV, dobivamo: \[E=28,13\cdot 10^{6}\,\textrm{eV}=28,13\,\textrm{MeV}\]
20. zadatak
Koja čestica X nastaje u navedenoj nuklearnoj reakciji? \[{_{\,\,7}^{14}}\,\textrm{N}+\alpha\rightarrow {_{\,\,8}^{17}}\,\textrm{O}+\textrm{X}\]
- A. neutron
- B. elektron
- C. pozitron
- D. proton
Pomoć potražite na poveznici Nuklearne reakcije.
Alfa-čestica je jezgra helijeva atoma \({_{2}^{4}}\,\textrm{He}\).
\[{_{\,\,7}^{14}}\,\textrm{N}+{_{2}^{4}}\,\textrm{He}\rightarrow{_{\,\,8}^{17}}\,\textrm{O}+{_{Z}^{A}}\,\textrm{X}\]
Prema zakonu očuvanja naboja možemo napisati 7 + 2 = 8 + Z pa dobijemo Z = 1.
Prema zakonu očuvanja broja nukleona imamo 14 + 4 = 17 + A i dobijemo A = 1.
Čestica s rednim i masenim brojem 1 je jezgra vodikova atoma, odnosno proton.
21. zadatak
Fotoni energije 5 eV izbijaju elektrone iz nekog metala. Najveći iznos
kinetičke energije izbijenih elektrona je 3 eV.
Koliki je izlazni rad metala?
- A. 2 eV
- B. 3 eV
- C. 5 eV
- D. 8 eV
Pomoć potražite na poveznici Fotoelektrični učinak.
Energija fotona koji padaju na metal pretvara se na svladavanje izlaznoga rada i kinetičku energiju izbačenih elektrona: \[E_{\textrm{f}}=W_{0}+E_{\textrm{k}}\] Izlazni rad je jednak: \[W_{0}=E_{\textrm{f}}-E_{\textrm{k}}=2\,\textrm{eV}\]
22. zadatak
Idealnom plinu se izohorno poveća temperatura za 300 K. Pritom mu se tlak poveća tri puta.
Kolika je bila početna temperatura plina?
- A. 100 K
- B. 150 K
- C. 300 K
Pomoć potražite na poveznici Izohorna promjena stanja plina.
Opća plinska jednadžba: \[\frac{p_{1}\,V_{1}}{T_1}=\frac{p_{2}\,V_{2}}{T_2}\] Za izohorne procese volumen plina je konstantan pa je \(V_{1}=V_{2}\). Opća plinska jednadžba prelazi u: \[\frac{p_{1}}{T_{1}}=\frac{p_{2}}{T_{2}}\] Prema zadatku je \(p_{2}=3\cdot p_{1}\) a \(T_{2}=T_{1}+300\). Nakon što uvrstimo \(p_{2}\) i \(T_{2}\), skratimo \(p_{1}\) te riješimo jednadžbu, za početnu temperaturu dobijemo: \(T_{1}=150\,\textrm{K}\)
23. zadatak
Okomito na optičku rešetku pada crvena i zelena monokromatska svjetlost.
Koja je od navedenih tvrdnji o kutu prvog ogibnog maksimuma točna?
- A. Kut je veći za crveno svjetlo.
- B. Kut je veći za zeleno svjetlo.
- C. Kut je jednak za obje valne duljine.
Pomoć potražite na poveznici Ogib svjetlosti na optičkoj rešetki.
Uvjet za maksimume koje daje optička rešetka: \[d\cdot \textrm{sin}\,\alpha=k\,\lambda\] Kutovi pod kojima se vide maksimumi k-tog reda, mogu se odrediti iz: \[\textrm{sin}\,\alpha=\frac{k\,\lambda}{d}\] Kut ogiba proporcionalan je valnoj duljini. Crvena svjetlost ima veću valnu duljinu od zelene, pa će se ogibati pod većim kutom.
24. zadatak
Raketa prolazi pored svemirske postaje brzinom v u smjeru paralelnom duljini rakete. Dežurni fizičar u postaji izmjeri da je
duljina rakete 25 m.
Koliku duljinu rakete mjeri putnik u raketi?
- A. manju od 25 m
- B. jednaku 25 m
- C. veću od 25 m
Pomoć potražite na poveznici Kontrakcija duljine
Kontrakciju duljine možemo prikazati kao: \[L=L_{0}\,\sqrt{1-v^{2}/c^2}\] \(L=25\,\textrm{m}\) (duljina koju mjeri fizičar u postaji); \(L_{0}\) je duljina koju mjeri putnik u raketi. Budući da je \[\sqrt{1-v^2/c^2} < 1\] slijedi: \[L < L_{0}\] Točan odgovor je C.
25. zadatak
Dobili ste dijamant. Izvagali ste ga i dobili sljedeće vrijednosti:
m1=8,15 g, m2=8,16 g,
m3=8,17 g, m4=8,19 g
i m5=8,23 g.
Kolika je srednja vrijednost ovog mjerenja i pripadna maksimalna apsolutna pogrješka?
\(\overline{m}\) = g
\(\left|\Delta m\right|\) = g
Srednja vrijednost
Srednja vrijednost jednaka je aritmetičkoj sredini kada smo izvršili nekoliko mjerenja neke fizičke veličine \(x\). Broj mjerenja označimo s \(n\):
\[\overline{x}=\frac{x_{1}+x_{2}+x_{3}\,+...+\,x_{n}}{n}\]
Maksimalna apsolutna pogreška
Odredimo odstupanja svakog pojedinog mjerenja od srednje vrijednosti:
\[\Delta x_{\textrm{i}}=x_{\textrm{i}}-\overline{x}\]
Iz ovako dobivenih odstupanja uzimamo ono koje je po apsolutnom iznosu najveće i to nazivamo maksimalnom apsolutnom pogreškom: \(\left|\Delta x\right|.\)
Srednja vrijednost: \[\overline{m}=\left(m_{1}+m_{2}+m_{3}+m_{4}+m_{5}\right)/5=\ 8,18\,\textrm{g}\] Maksimalna apsolutna pogreška: \[\left|\Delta m\right|=0,05\,\textrm{g}\]
26. zadatak
Tijelo mase 4 kg klizi niz kosinu jednolikom brzinom. Kut koji kosina zatvara s vodoravnom podlogom je 20 0.
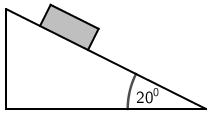
Koliki je iznos sile trenja koja djeluje na tijelo?
Odgovor: N
Koje sile djeluju na tijelo? Kolika je rezultantna sila ako tijelo niz kosinu klizi jednolikom brzinom?
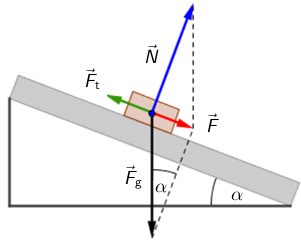
Na tijelo djeluju sila teža \(\vec{F}_{\textrm{g}}\), reakcija podloge \(\vec{N}\) i sila trenja \(\vec{F}_{\textrm{t}}\). Odredimo rezultantu sile teže i reakcije podloge: \[F=F_{\textrm{g}}\,\textrm{sin}\,\alpha=m\,g\,\textrm{sin}\,\alpha=13,7\,\textrm{N}\] Budući da se radi o jednolikom gibanju, rezultantna sila mora biti jednaka nuli, pa zaključujemo da i sila trenja, koja je suprotno orijentirana od sile \(\vec{F}\), također ima iznos od \(13,7\,\textrm{N}.\)
27. zadatak
Carnotov stroj radi između dvaju toplinskih spremnika, jednog temperature 10 0C
i drugog temperature 100 0C.
Kolika je korisnost tog stroja?
Odgovor:
Korisnost toplinskog stroja:
\[\eta=1-\frac{\left | Q_{2} \right |}{Q_{1}}\]
\(Q_{1}\) je toplina koju stroj prima od toplijeg spremnika, a \(Q_{2}\) toplina koju stroj predaje hladnijem spremniku.
Za Carnotov stroj korisnost možemo prikazati i pomoću temperatura toplijeg i hladnijeg spremnika, \(T_{1}\) i \(T_{2}\):
\[\eta=1-\frac{\left | T_{2} \right |}{T_{1}}\]
Korisnost Carnotovog toplinskog stroja jednaka je: \[\eta=\frac{T_{1}-T_{2}}{T_{1}}\] Nakon što temperature pretvorimo u kelvine, za korisnost dobijemo: \[\eta=0,24\] Korisnost možemo prikazati i u postocima: 24 %.
28. zadatak
Kolika je brzina elektrona koji se ubrzao kroz napon od 100 V?
Elektron je u početnoj točki mirovao.
Odgovor: m/s
Pomoć potražite na poveznici Serijski RCL krug.
Rad kojega obavi električno polje napona \(U\) za ubrzavanje elektrona iznosi \[W=e\,U\] Taj se rad pretvori u kinetičku energiju elektrona: \[E_{\textrm{k}}=\frac{m\,v^{2}}{2}\] Izjednačimo prethodne izraze i odredimo brzinu: \[\frac{m\,v^{2}}{2}=e\,U\] \[v=\sqrt{\frac{2\,e\,U}{m}}=5,93\cdot 10^{6}\,\textrm{m}/\textrm{s}\]
29. zadatak
Realni predmet je od divergentne leće udaljen 20 cm, a virtualna slika koja se vidi kroz leću je na udaljenosti
10 cm od leće.
Kolika je jakost leće?
Odgovor: \(\textrm{m}^{-1}\)
Jakost leće definirana je kao recipročna vrijednost žarišne duljine izražene u metrima: \[C = \frac{1}{f}\] Jakost leće mjerimo u dioptrijama: \[1 \textrm{dpt} = 1\,\textrm{m}^{-1}\] Jednadžba leće povezuje udaljenost predmeta od leće \(a\), udaljenost slike od leće \(b\), sa žarišnom udaljenošću, \(f\): \[\frac{1}{f} = \frac{1}{a} + \frac{1}{b}\] Udaljenosti \(a\) i \(b\) su pozitivne za realne predmete i slike, a negativne za virtualne. Žarišna daljina konvergentne leće je pozitivna, a divergentne negativna. Realna slika je obrnuta, a virtualna uspravna. Divergentna leća uvijek daje virtualnu sliku.
Uvrštavanjem podataka u jednadžbu leće dobijemo: \[\frac{1}{f} = \frac{1}{0,2}-\frac{1}{0,1}=-5\,\textrm{m}^{-1}\] Prema tome, \[C = -5\,\textrm{m}^{-1}\]
30. zadatak
Vrijeme poluraspada izotopa stroncija je 29 godina. Početna masa tog izotopa stroncija u uzorku je
60 g.
Kolika će biti masa tog izotopa stroncija u uzorku 100 godina kasnije?
Odgovor: g
Pomoć potražite na poveznici Zakon radioaktivnog raspada.
Prema zakonu radioaktivnog raspada, broj čestica koje preostanu nakon vremena \(t\) u uzorku jednak je: \[N=N_{0}\,e^{\large{-\textrm{ln}\,2\,\frac{t}{T}}}\] Masa uzorka proporcionalna je broju jezgri: \[m=m_{0}\,e^{\large{-\textrm{ln}\,2\,\frac{t}{T}}}\] Uvrštavanjem podataka \(T=29\,\textrm{god}\), \(t=100\,\textrm{god}\) i \(m_{0}=60\,\textrm{g}\), dobijemo \[m=5,5\,\textrm{g}\]
31. zadatak
Vagon mase 20 t giba se jednoliko po vodoravnoj pruzi brzinom 1 m/s te nalijeće na mirni
vagon mase 30 t.
Koliko se kinetičke energije pretvori u druge oblike energije ako se vagoni nakon sudara gibaju zajedno?
Odgovor: J
Pomoć potražite na poveznici Očuvanje energije u sudarima.
Brzinu vagona nakon sudara odredimo pomoću zakona očuvanja količine gibanja:
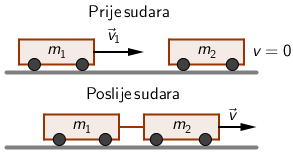
Drugi vagon prije sudara miruje pa je njegova količina gibanja jednaka nuli: \[m_{1}\,v_{1}=\left(m_{1}+m_{2}\right)\,{v}\] Brzina vagona nakon sudara je: \[v=\frac{m_{1}\,v_{1}}{\left(m_{1}+m_{2}\right)}=0,4\,\textrm{m}/\textrm{s}\] Kinetička energija prije sudara jednaka je (drugi vagon miruje): \[E_{\textrm{k}1}=\frac{m_1v_1^2}{2}=10000\,\textrm{J}\] Kinetička energija poslije sudara jednaka je (vagoni se gibaju zajedno): \[E_{\textrm{k}2}=\frac{\left(m_{1}+m_{2}\right)\,v^{2}}{2}=4000\,\textrm{J}\] U druge oblike energije pretvorilo se: \[\Delta E_{\textrm{k}}=E_{\textrm{k}1}-E_{\textrm{k}2}=6000\,\textrm{J}\]
32. zadatak
Grijačem snage 3 kW zagrijava se 0,5 kg vode čija je početna temperatura
25 0C.
Koliko je vremena potrebno da sva voda ispari? Zanemarite gubitke. Specifični toplinski kapacitet vode je
\(4200\,\textrm{J}\,\textrm{kg}^{-1}\,\textrm{K}^{-1}\), a njezina specifična toplina isparavanja je \(2,26\cdot 10^{6}\,\textrm{J}\,\textrm{kg}^{-1}.\)
Odgovor: s
Toplina potrebna za zagrijavanje tijela: \[Q=m\,c\,\Delta t\]
- \(m\)-masa tijela
- \(c\)-specifični toplinski kapacitet tijela
- \(\Delta t\)-porast temperature tijela tijela
- \(r\)-specifična toplina isparavanja
Vodi je potrebno dovesti toplinu potrebnu za zagrijavanje do 100 0C i toplinu potrebnu za isparavanje. \[Q=Q_{\textrm{zagrijavanje}}+Q_{\textrm{isparavanje}}\] \[Q=m\,c\left(t_{2}-t_{1}\right)+m\,r\] Električna energija koju daje grijač: \(W=P\,t\) pretvara se u potrebnu toplinu: \[W=Q\] Iz jednadžbe: \[P\,t=m\,c\left(t_{2}-t_{1}\right)+m\,r\] odredimo potrebno vrijeme: \[t=\frac{m\,c\left(t_{2}-t_{1}\right)+m\,r}{P}\] Uvrštavanjem zadanih podataka dobijemo: \[t = 429,2\,\textrm{s}\]
33. zadatak
Ampermetar ima mjerno područje 1 A i unutarnji otpor 0,1 Ω. Njime treba mjeriti
struje iznosa do 3 A.
Koliki je dodatni otpor potrebno spojiti s ampermetrom u strujnom krugu kako bi to bilo moguće?
Odgovor: \(\Omega\)
Napon na ampermetru je: \[U=I_{\small{\textrm{A}}}\,R_{\small{\textrm{A}}}=1\cdot 0,1=0,1\,\textrm{V}\] Ako želimo da uz taj napon ampermetar može pokazivati veću struju, moramo mu paralelno spojiti dodatni otpor \(R\).
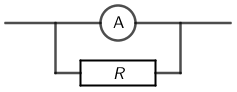
Napon na ampermetru i dodatnom otporu je isti kao i prije: \(U=I\,R_{\textrm{uk}}\).
- \(I=3\,\textrm{A}\)
- \(R_{\textrm{uk}}\) - ukupni otpor ampermetra i dodatnog otpora \(R\)
34. zadatak
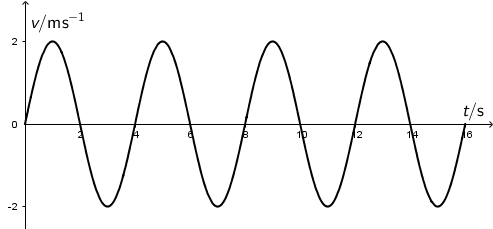
Graf prikazuje brzinu u ovisnosti o vremenu titranja jednostavnog njihala.
Kolika je amplituda titranja tog njihala?
Odgovor: m
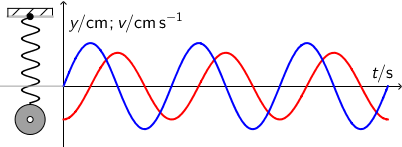
Jednadžba elongacije harmonijskog titranja:
\[y=y_{0}^{\,}\,\textrm{sin}\,\left(\omega\,t+\varphi_{0}\right)\]
Jednadžba brzine harmonijskog titranja:
\[v=\omega\,y_{0}^{\,}\,\textrm{cos}\,\left(\omega\,t+\varphi_{0}\right)\]
Napomena
Na crtežu je graf elongacije označen crvenom, a graf brzine plavom bojom.
Početna faza je:
\[\varphi_{0}^{\,}=\frac{3}{2}\,\pi\]
Iz grafa pročitamo da je maksimalna brzina jednaka \(v_{0}=2\,\textrm{m}/\textrm{s}\) a period \(T=4\,\textrm{s}.\) Maksimalnu brzinu prikazujemo izrazom: \[v_0^{\,}=\frac{2\,y_{0}^{\,}\,\pi}{T}\] Ovdje je \(y_{0}^{\,}\) amplituda titranja. Ako riješimo ovu jednadžbu, za amplitudu dobivamo: \[y_{0}^{\,}=\frac{v_{0}^{\,}\,T}{2\,\pi}=\frac{4}{\pi}=1,27\,\textrm{m}\]
35. zadatak
Na energetskom dijagramu pomoću strjelice prikažite apsorpciju fotona koji ima najveću valnu duljinu za dane energetske nivoe.
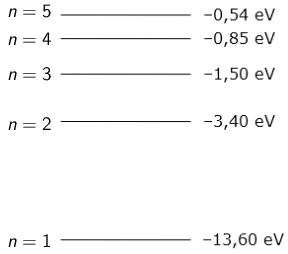
Odgovor: m
Pomoć potražite na poveznici Apsorpcija fotona.
Ukoliko atom apsorbira foton odgovarajuće energije, prijeći će u neko pobuđeno stanje. Neka se atom nalazi u stanju u kojemu ima energiju \(E_{\textrm{n}}\). Ako atom apsorbira foton energije \(E_{\textrm{f}}\), prijeći će u više energijsko stanje u kojemu će mu energija biti \(E_{\textrm{m}}=E_{\textrm{n}}+E_{\textrm{f}}.\) Energiju fotona možemo prikazati kao: \[E_{\textrm{f}}=\frac{h\,c}{\lambda}\] Za valnu duljinu apsorbiranog fotona dobivamo: \[\lambda=\frac{h\,c}{E_{\textrm{m}}-E_{\textrm{n}}}\] Vidimo da je valna duljina apsorbiranog fotona obrnuto razmjerna razlici energetskih nivoa. Prema tome, atom će apsorbirati foton najveće valne duljine za prijelaz koji odgovara najmanjoj razlici energija. Iz crteža je vidljivo da se radi o prijelazu iz stanja \(n=4\) u stanje \(n=5.\)
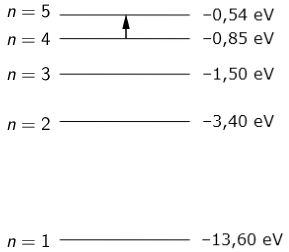
Valna duljina jednaka je: \[\lambda=\frac{h\,c}{E_{5}-E_{4}}\] Ako uvrstimo podatke (energiju je potrebno iz eV pretvoriti u J), dobijemo \[\lambda=4·10^{-6}\,\textrm{m}.\]