Ljetni rok 2011. godine
1. zadatak
1. Koji od grafova prikazuje ovisnost brzine o vremenu za jednoliko ubrzano gibanje?
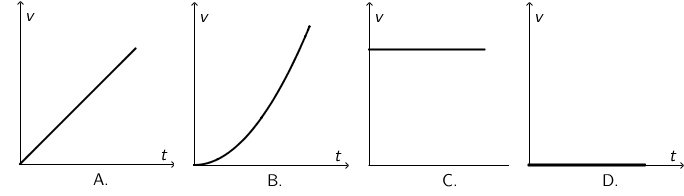
- A. Graf A.
- B. Graf B.
- C. Graf C.
- D. Graf D.
Pomoć potražite na poveznici Jednoliko ubrzano pravocrtno gibanje.
Jednoliko ubrzano gibanje je gibanje kod kojega je akceleracija stalna, što znači da je graf brzine pravac koji s osi \(t\) zatvara kut manji od 90 stupnjeva. Graf C odgovara jednolikom gibanju, a graf D mirovanju. Graf B je graf brzine pri nejednoliko ubrzanom gibanju jer se akceleracija koja je jednaka nagibu tangente u nekom trenutku stalno povećava.
2. zadatak
Na tijelo djeluje ukupna sila koja se mijenja duž puta kako je prikazano na grafu. Tijelo početno miruje
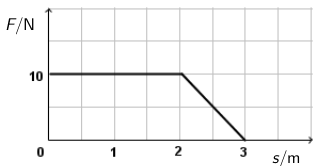
Koliko iznosi kinetička energija tijela nakon što je ono prešlo 3 m? Trenje se zanemaruje.
- A. 0 J
- B. 20 J
- C. 25 J
- D. 30 J
Vektor količine gibanja: \[\vec{p}=m\,\vec{v}\]
Kinetička energija jednaka je obavljenom radu. Pomoću \(F,s\) grafa rad određujemo kao površinu ispod grafa. Možemo ju odrediti kao zbroj površine pravokutnika i površine trokuta ili kao površinu trapeza: \[W=\frac{3+2}{2}\cdot 10=25\,\textrm{J}\]
3. zadatak
Kada je potpuno uronjeno u tekućinu, tijelo mase 1,5 kg istisne 0,8 kg tekućine.
Što od navedenoga vrijedi za silu uzgona na tijelo?
- A. Sila uzgona iznosi 7 N i usmjerena je prema gore.
- B. Sila uzgona iznosi 7 N i usmjerena je prema dolje.
- C. Sila uzgona iznosi 8 N i usmjerena je prema gore.
- D. Sila uzgona iznosi 8 N i usmjerena je prema dolje.
Pomoć potražite na poveznici Arhimedov zakon.
Sila uzgona na tijelo uronjeno u tekućinu je: \[F_{\textrm{u}}=\rho\,g\,V\] Volumen uronjenog tijela je \(V\) i on je jednak volumenu istisnute tekućine. Zbog toga je masa istisnute tekućine jednaka: \[m_{\textrm{tekućine}}=ρ\cdot V\] Prema tome, silu uzgona možemo prikazati kao: \[F_{\textrm{u}}=m_{\textrm{tekućine}}\cdot g\] Sila uzgona jednaka je težini istisnute tekućine. Kako je masa istisnute tekućine 0,8 kg, sila uzgona jednaka je 8 N i usmjerena je prema gore.
4. zadatak
Akceleracija slobodnoga pada na površini Mjeseca je \(g_{\small{\textrm{M}}}\). Polumjer Mjeseca je \(R\).
Kolika je akceleracija slobodnoga pada na udaljenosti \(2\,R\) od površine Mjeseca?
- A. \(\large{\frac{g_{\small{\textrm{M}}}}{9}}\)
- B. \(\large{\frac{g_{\small{\textrm{M}}}}{3}}\)
- C. \(\large{\frac{g_{\small{\textrm{M}}}}{2}}\)
- D. \({2\,g_{\small{\textrm{M}}}}\)
Pomoć potražite na poveznici Sila teža.
Usporedimo izraze za silu težu, koja je zapravo sila opće gravitacije: \[F_{\textrm{g}}=G\,\frac{M\,m}{R^{2}}\] i silu težu pomoću drugog Newtonovog zakona: \[F_{\textrm{g}}=m\,g\] Vidimo da je akceleracija slobodnoga pada jednaka: \[g=G\,\frac{M}{R^{2}}\] Točka koja se nalazi na površini Mjeseca udaljena je za \(R\) od njegovog središta, a točka koja se nalazi na udaljenosti \(2\,R\) od površine Mjeseca, udaljena je \(3\,R\) od njegovog središta, dakle tri puta više od točke na površini. Zbog toga je akceleracija slobodnog pada devet puta manja.
5. zadatak
Iz helikoptera koji leti u horizontalnome smjeru ispušten je paket.
Što je za promatrača na tlu putanja paketa ako se zanemari utjecaj otpora zraka na paket?
- A. dio pravca
- B. dio kružnice
- C. dio elipse
- D. dio parabole
Pomoć potražite na poveznici Horizontalni hitac.

Na slici je crvenom bojom nacrtan dio parabole.
6. zadatak
Potrebno je povećati korisnost idealnoga toplinskoga stroja. Može se povećati temperatura toplijega spremnika za \(\Delta T\) ili smanjiti temperatura hladnijega spremnika za isti iznos \(\Delta T\).
- A. Korisnost će biti veća ako se poveća temperatura toplijega spremnika za \(\Delta T\).
- B. Korisnost će biti veća ako se smanji temperatura hladnijega spremnika za \(\Delta T\).
- C. Korisnost će se povećati jednako u obama slučajevima.
- D. Korisnost se ne će promijeniti zbog promjene temperature spremnika topline.
Korisnost idealnog (Carnotovog) toplinskoga stroja jednaka je: \[\eta=\frac{T_{1}-T_{2}}{T_{1}}\]
Ako povećamo temperaturu toplijeg spremnika za \(\Delta T\), korisnost će biti: \[\eta_{1}=\frac{T_{1}+\Delta T-T_{2}}{T_1+\Delta T}=\frac{T_{1}-T_{2}+\Delta T}{T_{1}+\Delta T}\] Ako smanjimo temperaturu hladnijeg spremnika za \(\Delta T\), korisnost će biti: \[\eta_{2}=\frac{T_{1}-\left(T_{2}-\Delta T\right)}{T_{1}}=\frac{T_{1}-T_{2}+\Delta T}{\Delta T}\] Usporedbom ova dva izraza zaključujemo: \[\eta_{1} < \eta_{2}\]
7. zadatak
Idealni plin temperature \(T\) zagrije se tako da se srednja kinetička energija nasumičnoga gibanja njegovih čestica udvostruči.
Kolika je temperatura plina nakon zagrijavanja?
- A. \(T/\sqrt{2}\)
- B. \(T\,\sqrt{2}\)
- C. \(2\,T\)
- D. \(6\,T\)
Pomoć potražite na poveznici Srednja kinetička energija molekularnog gibanja.
Srednja kietička energija jednoatomnog idealnog plina: \[\bar{E_{\textrm{k}}}=\frac{3}{2}k\,T\] Srednja kietička energija dvoatomnog idealnog plina: \[\bar{E_{\textrm{k}}}=\frac{5}{2}k\,T\] Zbog proporcionalnosti apsolutne temperature idealnoga plina i srednje kinetičke energije molekularnoga gibanja, dvostruki porast te energije prouzrokovat će i dvostruki porast temperature.
8. zadatak
Specifična toplina isparavanja vode iznosi 2260 kJ/kg. Vodena para mase 0,5 kg
i temperature 100 0C kondenzira se u vodu
temperature 100 0C.
Koja se od navedenih izmjena topline dogodila tijekom toga procesa?
- A. Iz pare je u okolinu prenesena toplina od 1130 kJ.
- B. Iz okoline je na paru prešla toplina od 1130 kJ.
- C. Iz pare je u okolinu prenesena toplina od 2260 kJ.
- D. Iz okoline je na paru prešla toplina od 2260 kJ.
Toplina potrebna za zagrijavanje tijela: \[Q=m\,c\,\Delta t\]
- \(m\)-masa tijela
- \(c\)-specifični toplinski kapacitet tijela
- \(\Delta t\)-porast temperature tijela tijela
- \(r\)-specifična toplina isparavanja
- \(\lambda\)-specifična toplina taljenja
Specifična toplina isparavanja je količina topline potrebna da se 1 kg neke tvari iz tekućine pretvori u paru: \[r=\frac{Q_{\textrm{i}}}{m}\] Toplina isparavanja ili kondenzacije jednaka je: \[Q_{\textrm{i}}=r\,m=2260\cdot 0,5=1130\,\textrm{J}\] Kod isparavanja voda prima toplinu, a kod kondenziranja vodena para oslobađa toplinu, odnosno, predaje ju okolini.
9. zadatak
Učenici su izmjerili sljedeće vrijednosti napona na polovima neopterećene baterije:
1,50 V, 1,51 V, 1,53 V i 1,50 V.
Koji od predloženih odgovora predstavlja ispravan zapis rezultata toga mjerenja?
- A. (1,50 ± 0,03) V
- B. (1,50 ± 0,01) V
- C. (1,51 ± 0,02) V
- D. (1,51 ± 0,03) V
Srednja vrijednost
Srednja vrijednost jednaka je aritmetičkoj sredini kada smo izvršili nekoliko mjerenja neke fizičke veličine \(x\). Broj mjerenja označimo s \(n\):
\[\overline{x}=\frac{x_{1}+x_{2}+x_{3}\,+...+\,x_{n}}{n}\]
Maksimalna apsolutna pogreška
Odredimo odstupanja svakog pojedinog mjerenja od srednje vrijednosti:
\[\Delta x_{\textrm{i}}=x_{\textrm{i}}-\overline{x}\]
Iz ovako dobivenih odstupanja uzimamo ono koje je po apsolutnom iznosu najveće i to nazivamo maksimalnom apsolutnom pogreškom: \(\left|\Delta x\right|.\)
Nakon što izračunamo srednju vrijednost i odredimo maksimalnu apsolutnu pogrešku, vidimo da je točan rezultat: \[\left(1,51 ± 0,02\right)\,\textrm{V}\]
10. zadatak
Baterija u strujnome krugu prikazanome na crtežu ima elektromotorni napon E. Smatra se da su ampermetar i voltmetar idealni.
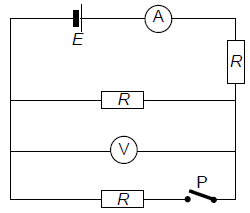
Kako će se promijeniti iznosi na mjernim uređajima kada se zatvori prekidač P?
- A. Iznos na ampermetru će se povećati, a na voltmetru smanjiti.
- B. Povećat će se iznosi i na ampermetru i na voltmetru.
- C. Iznos na ampermetru će se smanjiti, a na voltmetru povećati.
- D. Smanjit će se iznosi i na ampermetru i na voltmetru.
Pomoć potražite na poveznici Spajanje otpora i Kirchhoffova pravila.
Prije zatvaranja prekidača ukupni je otpor kruga \(2\,R\), a nakon što prekidač zatvorimo ukupni je otpor \(1,5\,R\) pa će se struja povećati i
ampermetar će pokazivati veću struju (Ohmov zakon).
Zbog povećanja struje kroz otpor koji je serijski spojen s ampermetrom, napon na njemu će se povećati \(\left(U=I\,R\right)\), što znači da će se
napon na otporima koji su paralelno spojeni s voltmetrom smanjiti i voltmetar će pokazivati manju vrijednost
(prema drugom Kirchhoffovom pravilu zbroj padova napona u krugu struje jednak je naponu izvora struje).
11. zadatak
Na grafu je prikazana ovisnost jakosti struje \(I\) o naponu \(U\) za dva vodiča.
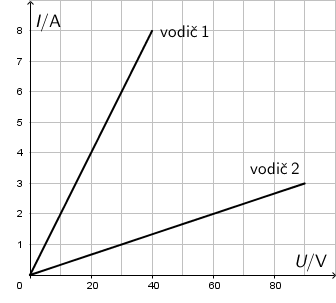
Koliko bi iznosio ukupni otpor serijskoga spoja tih dvaju vodiča?
- A. \(0,23\,\Omega\)
- B. \(4,3\,\Omega\)
- C. \(25\,\Omega\)
- D. \(35\,\Omega\)
Pomoć potražite na poveznici Spajanje otpora.
Koristeći Ohmov zakon i podatke koje čitamo iz grafa, zaključujemo da vodič 1 ima otpor: \[R_{1}=\frac{40}{8}=5\,\Omega\] Na sličan način odredimo otpor vodiča 2: \[R_{2}=\frac{60}{2}=30\,\Omega\] Ako ih spojimo serijski, ukupni je otpor: \[R_{\textrm{s}}=R_{1}+R_{2}=35\,\Omega\]
12. zadatak
Dva točkasta naboja u zraku se međusobno odbijaju silom 2 μN. Naboji su smješteni na jednak razmak u sredstvo
relativne dielektrične konstante 8.
Kolika je sila između tih naboja u navedenome sredstvu?
- A. 0 N
- B. 0,25 μN
- C. 2 μN
- D. 16 μN
Pomoć potražite na poveznici Coulombov zakon.
Električna sila između dva točkasta naboja u sredstvu: \[F=\frac{k}{\epsilon_{\textrm{r}}}\,\frac{q_{1}\,q_{2}}{r^{2}}\] Električna sila između ta dva naboja na jednakoj udaljenosti u vakuumu: \[F_{0}=k\,\frac{q_{1}\,q_{2}}{r^{2}}\] Podijelimo ova dva izraza: \[\frac{F}{F_0}=\frac{1}{\epsilon_{\textrm{r}}}\] \[F=\frac{F_{0}}{\epsilon_{\textrm{r}}}=0,25\,\mu\textrm{N}\]
13. zadatak
Konvergentna leća stvara sliku predmeta na zastoru udaljenome 12 cm od leće.
Žarišna daljina leće je 6 cm.
Kolika je udaljenost između predmeta i slike toga predmeta?
- A. 18 cm
- B. 20 cm
- C. 22 cm
- D. 24 cm
Pomoć potražite na poveznici Jednadžba leće.
Iz jednadžbe leće: \[\frac{1}{a}+\frac{1}{b}=\frac{1}{f}\] za udaljenost predmeta dobijemo: \[\frac{1}{a}=\frac{1}{f}-\frac{1}{b}\] Rješavanjem jednadžbe dobijemo: \[a=12\,\textrm{cm}\] Udaljenost premeta i slike je \[a+b=24\,\textrm{cm}\]
14. zadatak
Točkasti izvor vala titra frekvencijom 50 Hz. Val se širi brzinom od 300 m/s.
Kolika je razlika u fazi između točaka koje su 2 m i 8 m udaljene od izvora?
- A. 0 rad
- B. π rad
- C. 6 rad
- D. 2π rad
Jednadžba harmonijskog vala: \[y=A\,\textrm{sin}\left (\frac{2\,\pi}{T}\,t - \frac{2\,\pi}{\lambda}\,x\right)\]
- \(y\) - elongacija čestice u trenutku \(t\) na mjestu koje je za \(x\) udaljeno od izvora vala.
- \(A\) - amplituda vala.
- \(T\) - period titranja izvora vala.
- \(\lambda\) - valna duljina.
Jednadžba titranja čestice koja je udaljena od izvora vala za \(x\) u trenutku \(t\):
\[y=A\,\textrm{sin}\left (\frac{2\,\pi}{T}\,t - \frac{2\,\pi}{\lambda}\,x\right)\]
Veličinu u zagradi nazivamo fazom vala u trenutku \(t\) na mjestu koje je za \(x\) udaljeno od izvora vala:
\[\varphi=\frac{2\,\pi}{T}\,t-\frac{2\,\pi}{\lambda}\,x\]
Ako su dvije točke u trenutku \(t\) udaljene od izvora vala za \(x_{1}\) i \(x_{2}\), razlika faza između njih je:
\[\Delta\varphi=\frac{2\,\pi}{\lambda}\,\left(x_{2}-x_{1}\right)\]
Valnu duljinu dobijemo pomoću brzine vala i frekvencije izvora:
\[\lambda=\frac{v}{f}=6\,\textrm{m}\]
Razlika u fazi je:
\[\Delta\varphi=2\,\pi\,\textrm{rad}\]
Napomena:
Veličinu
\[\Delta x=\left(x_{2}-x_{1}\right)\]
nazivamo razlikom hoda pa razliku faza možemo prikazati i kao:
\[\Delta\varphi=\frac{2\,\pi}{\lambda}\,\Delta x\]
15. zadatak
Vremenska ovisnost elongacije tijela koje harmonijski titra dana je izrazom \[y=2\,\textrm{cm}/\textrm{sin}\,\left(\pi\,\textrm{s}^{-1}\,t\right)\] Kako glasi izraz za brzinu toga tijela u ovisnosti o vremenu?
- A. \(v=2\,\textrm{cm}/\textrm{s}\,\textrm{sin}\,\left(2\,\pi\,\textrm{s}^{-1}\,t\right)\)
- B. \(v=2\,\pi\,\textrm{cm}/\textrm{s}\,\textrm{sin}\,\left(\pi\,\textrm{s}^{-1}\,t\right)\)
- C. \(v=2\,\textrm{cm}/\textrm{s}\,\textrm{cos}\,\left(2\,\pi\,\textrm{s}^{-1}\,t\right)\)
- D. \(v=2\,\pi\,\textrm{cm}/\textrm{s}\,\textrm{cos}\,\left(\pi\,\textrm{s}^{-1}\,t\right)\)
Ako se elongacija kod harmonijskog titranja mijenja kao: \[y=y_{0}\,\textrm{sin}\,\omega\, t=y_{0}\,\textrm{sin}\,\frac{2\,\pi}{T}\, t\] onda se brzina mijenja kao: \[v=v_{0}\,\textrm{cos}\,\omega\,t=v_{0}\,\textrm{cos}\,\frac{2\,\pi}{T}\, t\] Maksimalna brzina harmonijskog titranja: \[v_{0}=\omega\,y_{0}=\frac{2\,\pi}{T}\,y_{0}\] Više o nastanku vala na užetu potražite na poveznici Brzina harmonijskog titranja.
Jednadžba elongacije harmonijskog titranja je: \[y=y_{0}\,\textrm{sin}\,\omega\, t\] Uspoređivanjem sa zadanom jednadžbom za amplitudu titranja dobivamo \(y_{0}=2\,\textrm{cm}\), dok je kružna frekvencija \(\omega=\pi\,\textrm{rad}.\) Najveća brzina kod harmonijskog titranja je: \[v_{0}=\frac{2\,\pi\,y_0}{T}=\omega\,y_0=2\,\pi\,\textrm{cm}/\textrm{s}\] Ako se elongacija harmonijskog titranja mijenja kao funkcija sinus, onda se brzina mijenja kao funkcija kosinus: \[v=v_{0}\,\textrm{cos}\,\left(\omega\,t\right)\] \[v=2\,\pi\,\textrm{cm}/\textrm{s}\,\textrm{cos}\,\left(\pi\,\textrm{s}^{-1}\,t\right)\]
16. zadatak
Infracrveno zračenje valne duljine 2 μm nailazi na pregradu s dvjema pukotinama međusobnoga razmaka
1 mm. Maksimumi interferencije detektiraju se na udaljenosti 1 m od pregrade.
Koliki je razmak između susjednih maksimuma interferencije?
- A. 1 mm
- B. 2 mm
- C. 3 mm
- D. 4 mm
Pomoć potražite na poveznici Youngov pokus.
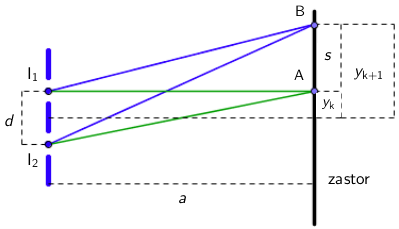
Udaljenost k-tog maksimuma od središta zastora je: \[y_{\textrm{k}}=\frac{k\,\lambda\,a}{d}\] Udaljenost između dva susjedna maksimuma je: \[s=y_{k+1}-y_{k}=\frac{\lambda\,a}{d}=2\cdot 10^{-3}\,\textrm{m}=2\,\textrm{mm}\]
17. zadatak
Tijelo vezano na oprugu titra oko ravnotežnoga položaja.
Kako se naziva najveći pomak od ravnotežnoga položaja?
- A. period
- B. frekvencija
- C. elongacija
- D. amplituda
Najveću elongaciju titranja nazivamo amplitudom.
18. zadatak
Od 10 000 jezgri nekoga radioaktivnoga izotopa u prva se četiri dana raspadne 5000 jezgri.
Koja je od navedenih tvrdnji točna?
- A. U prva se dva dana raspalo 2 500 jezgri.
- B. U prva se dva dana raspalo 500 jezgri.
- C. U prva se dva dana raspalo više jezgri nego u sljedeća dva dana.
- D. Svaki se dan raspadne jednaki broj jezgri
Pomoć potražite na poveznici Zakon radioaktivnog raspada.
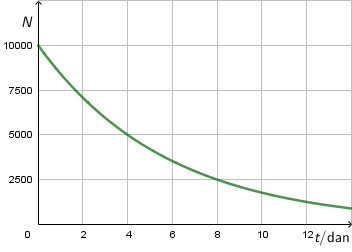
Iz grafa vidimo da je broj raspada u jedinici vremena veći na početku i da se smanjuje tijekom vremena. Prema tome, točan je odgovor C.
19. zadatak
Kojoj vrsti zračenja pripadaju fotoni energije 2 eV?
- A. gama zračenju
- B. vidljivoj svjetlosti
- C. mikrovalnomu zračenju
- D. radiovalovima
Pomoć potražite na poveznici Nuklearne reakcije.
Energiju fotona možemo prikazati kao: \[E=\frac{h\,c}{\lambda}\] Za valnu duljinu dobijemo: \[\lambda=\frac{h\,c}{E}=6,21\cdot 10^{-7}\,\textrm{m}=621\,\textrm{nm}\] Izračunata valna duljina pripada vidljivoj svjetlosti.
20. zadatak
Na crtežu je shematski prikazan dio energijskoga spektra nekoga atoma.
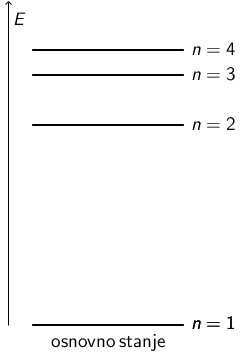
Za koji od navedenih prijelaza s jedne energijske razine na drugu elektron treba primiti najveću energiju?
- A. za n = 1 → n = 2
- B. za n = 2 → n = 1
- C. za n = 2 → n = 4
- D. za n = 4 → n = 2
Pomoć potražite na poveznici Apsorpcija fotona.
Iz crteža se vidi da je za prijelaz iz prve u drugu energijsku razinu potrebna najveća energija: \[E_{2} - E_{1}\]
21. zadatak
Kolika je temperatura na površini zvijezde čiji je intenzitet zračenja maksimalan na valnoj duljini 400 nm?
Pretpostavite da zvijezda zrači kao apsolutno crno tijelo.
- A. 3613 K
- B. 5109 K
- C. 7225 K
- D. 9050 K
Pomoć potražite na poveznici Wienov zakon.
Iz Wienovog zakona \[\lambda_{\textrm{maks}}\cdot T=b\] slijedi da je temperatura jednaka \[T=\frac{b}{\lambda_{\textrm{maks}}}=7225\,\textrm{K}\]
22. zadatak
Kružna ploča položena je vodoravno te se vrti oko vertikalne osi kroz središte stalnom kutnom brzinom.
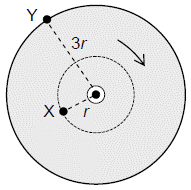
Novčić X nalazi se na tri puta manjoj udaljenosti od središta ploče nego novčić Y.
Kako se odnose njihove obodne brzine?
- A. \(v_{\small{\textrm{X}}}=v_{\small{\textrm{Y}}}/3\)
- B. \(v_{\small{\textrm{X}}}=v_{\small{\textrm{Y}}}\)
- C. \(v_{\small{\textrm{X}}}=2\,v_{\small{\textrm{Y}}}\)
Pomoć potražite na poveznici Jednoliko kružno gibanje.
Kada tijelo, koje se giba jednoliko po kružnici, za vrijeme \(\Delta t\) stigne iz točke A u točku B, polumjer kružnice opiše kut \(\Delta\alpha\), a tijelo prijeđe put koji je jednak duljini kružnog luka \(\Delta s\).
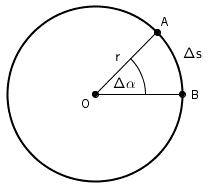
Obodna i kutna brzina, \(v\) i \(\omega\), definirane su kao: \[v=\frac{\Delta s}{\Delta t}; \omega=\frac{\Delta\alpha}{\Delta t}\] Nakon što tijelo obiđe kružnicu vrijedi \[\Delta t=T;\Delta s=2\,r\pi;\Delta \alpha=2\,\pi\] Za obodnu i kutnu brzinu dobijemo \[v=\frac{2\,r\,\pi}{T}; \omega=\frac{2\,\pi}{T}\] Iz posljednje dvije jednadžbe slijedi: \[v=\omega\,r\] Primijenimo ovu jednadžbu na točke X i Y: \[v_{\small{\textrm{X}}}=\omega\,r; v_{\small{\textrm{Y}}}=\omega\cdot 3\,r\] Nakon što jednadžbe podijelimo dobijemo \[\frac{v_{\small{\textrm{X}}}}{v_{\small{\textrm{Y}}}}=\frac{1}{3}\] \[v_{\small{\textrm{X}}}^{\,}=\frac{v_{\small{\textrm{Y}}^{\,}}}{3}\]
23. zadatak
Negativno nabijeni štap približi se bez doticanja nenabijenomu elektroskopu. Kazaljka se elektroskopa otkloni.
Kakav je pritom ukupni naboj na elektroskopu?
- A. pozitivan
- B. negativan
- C. jednak nuli
Pomoć potražite na poveznici Električni naboj.
Ako neutralnom tijelu približimo (bez doticanja) nabijeni štap, u tijelu dolazi do razdvajanja naboja, ali ono kao cjelina ostaje neutralno.
24. zadatak
Pločica od cinka obasjana je monokromatskim elektromagnetskim zračenjem koje izbacuje elektrone iz cinka.
Na koji se način može povećati broj izbačenih elektrona?
- A. povećanjem intenziteta zračenja
- B. povećanjem frekvencije zračenja
- C. povećanjem valne duljine zračenja
Pomoć potražite na poveznici Fotoelektrični učinak
Ukoliko na metal pada svjetlost većeg intenziteta, to znači da će u njoj biti više fotona. Više fotona znači veću vjerojatnost da će biti pogođeno više elektrona u metalu i time će ih više biti i izbačeno.
25. zadatak
Balon mase
Kolikom akceleracijom pada balon?
Odgovor: \(\textrm{m}/\textrm{s}^{2}\)
Odredite rezultantu sila koje djeluju na balon i primijenite temeljni zakon gibanja.
Na balon djeluju:
- sila teža \(\vec{F_{\textrm{g}}}\) vertikalno prema dolje
- sila otpora zraka \(\vec{F_{\textrm{o}}}\) vertikalno prema gore
- sila uzgona \(\vec{F_{\textrm{u}}}\) vertikalno prema gore
26. zadatak
Tijelo mase 3 kg guramo jednoliko duž kosine koja je dugačka 4 m,
a visoka 2 m. Trenje zanemarujemo.
Koliki se rad izvrši nad tijelom ako ga se gura od dna do vrha kosine?
Odgovor: J
Zadatak je najjednostavnije riješiti primjenom zakona očuvanja mehaničke energije.
Početna energija jednaka je: \[E_{1}=E_{\textrm{p}1}+E_{\textrm{k}1}\] Konačna energija jednaka je: \[E_{2}=E_{\textrm{p}2}+E_{\textrm{k}2}\] Budući da je gibanje jednoliko, kinetička se energija ne mijenja: \[E_{\textrm{k}1}=E_{\textrm{k}2}\] Rad je jednak promjeni mehaničke energije: \[W=E_{2}-E_{1}=E_{\textrm{p}2}+E_{\textrm{k}2}-\left(E_{\textrm{p}1}+E_{\textrm{k}1}\right)=E_{\textrm{p}2}-E_{\textrm{p}1}\] Za rad dobijemo: \[W\ =m\,g\,h-0=m\,g\,h=60\,\textrm{J}\]
27. zadatak
Obujam idealnoga plina pri temperaturi od 293 K je 1 m3.
Pri stalnome tlaku temperatura idealnoga plina naraste na 353 K.
Odredite obujam plina pri toj temperaturi.
Odgovor: \(\textrm{m}^{3}\)
Primijenite jednadžbu za izobarnu promjenu stanja idealnog plina.
Za izobarne procese vrijedi: \[\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}\] Ako uvrstimo zadane podatke, dobijemo: \[V_{2}=\frac{V_{1}\,T_{2}}{T_{1}}=1,2\,\textrm{m}^{3}\]
28. zadatak
Zavojnica induktiviteta 0,25 H i kondenzator serijski su spojeni na izvor izmjeničnoga napona
frekvencije 60 Hz.
Izračunajte kapacitet kondenzatora ako je njegov kapacitivni otpor jednak induktivnomu otporu zavojnice.
Odgovor: \(\mu F\)
Pomoć potražite na poveznici Induktivni otpor.
Kapacitivni otpor: \[R_{\small{\textrm{C}}}=\frac{1}{C\,\omega}\] Induktivni otpor: \[R_{\small{\textrm{L}}}=L\,\omega\] Izjednačimo ove otpore: \[\frac{1}{C\,\omega}=L\,\omega\] Iz ove jednadžbe odredimo kapacitet kondenzatora: \[C=\frac{1}{L\,\omega^{2}}=2,8\cdot 10^{-5}\,\textrm{F}=28\,\mu\textrm{F}\]
29. zadatak
Zraka svjetlosti upada iz zraka pod kutom od 600 prema okomici na mirnu površinu tekućine.
Izračunajte apsolutni indeks loma tekućine ako je kut između odbijene i lomljene zrake 900.
Odgovor:
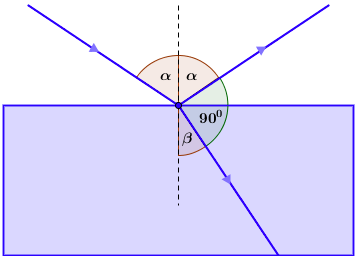
Zakon loma: \[n=\frac{\textrm{sin}\,\alpha}{\textrm{sin}\,\beta}\] \[\alpha+\beta=90^{0}\] \[n=\frac{\textrm{sin}\,\alpha}{\textrm{sin}\,\left(90^{0}-\alpha\right)}\] \[n=\frac{\textrm{sin}\,\alpha}{\textrm{cos}\,\alpha}\] \[n=\textrm{tg}\,\alpha\] To je Brewsterov zakon.
Prema Brewsterovom zakonu, indeks loma je: \[n=\textrm{tg}\,\alpha=1,73\]
30. zadatak
Astronautkinja putuje raketom koja se giba jednoliko po pravcu brzinom \(c\sqrt 3/2\) u odnosu na Zemlju. Ona je u svojem sustavu izmjerila
da njezino putovanje traje 2 god.
Koliko je vremena putovanje trajalo za promatrača na Zemlji?
Odgovor: god
Pomoć potražite na poveznici Dilatacija vremena.
Za promatrača na Zemlji proteklo je vrijeme: \[T=\frac{T_{0}}{\sqrt{1-v^{2}/c^{2}}}\] Uvrštavanjem zadanih podataka dobijemo \[T=4\,\textrm{god}\]
31. zadatak
Na tijelo mase 30 kg djeluje se silom F pod kutom od 300 prema horizontali.
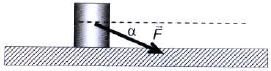
Tijelo se giba jednoliko. Faktor trenja između tijela i podloge je 0,1.
Odredite iznos sile F.
Odgovor: N
Odredite rezultantu svih sila koje na tijelo djeluju. Kolika je rezultantna sila ako se tijelo giba jednoliko?
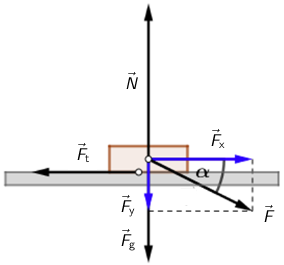
Budući da se tijelo ne giba u vertikalnom smjeru, ukupna sila u vertikalnom smjeru mora biti jednaka nuli. To znači da je reakcija podloge \(N\) jednaka: \[N=F_{\textrm{y}}+F_{\textrm{g}}=F\,\textrm{sin}\,\alpha+m\,g\] Sila trenja jednaka je: \[F_{\textrm{t}}=\mu\,N\] Rezultanta sila u horizontalnom smjeru također mora biti jednaka nuli jer se tijelo giba jednolikom brzinom: \[F_{\textrm{x}}=F_{\textrm{t}}\] \[F_{\textrm{x}}=\mu\,N\] \[F\,\textrm{cos}\,\alpha=\mu\,\left(F\,\textrm{sin}\,\alpha+m\,g\right)\] Tražena sila \(F\) jednaka je: \[F=\frac{\mu\,m\,g}{\textrm{cos}\,\alpha-\mu\,\textrm{sin}\,\alpha}=36,8\,\textrm{N}\]
32. zadatak
Grijačem snage 500 W tali se 2 kg
leda temperature 0 0C. Sva energija koju proizvede grijač potroši se na taljenje leda.
Za koliko se vremena led rastali? Specifična toplina taljenja leda iznosi 330000 J/kg.
Odgovor: s
Toplina potrebna za zagrijavanje tijela: \[Q=m\,c\,\Delta t\]
- \(m\)-masa tijela
- \(c\)-specifični toplinski kapacitet tijela
- \(\Delta t\)-porast temperature tijela tijela
- \(r\)-specifična toplina isparavanja
- \(\lambda\)-specifična toplina taljenja
Toplina potrebna za taljenje leda: \[Q_{\textrm{t}}=\lambda\,m\] Tu toplinu led dobiva od grijača snage \(P=500\,\textrm{W}\): \[Q_{\textrm{t}}=P\,t\] Iz ova dva izraza dobijemo vrijeme potrebno za taljenje leda: \[t=\frac{\lambda\,m}{P}=1320\,\textrm{s}\]
33. zadatak
Dva duga, ravna i međusobno paralelna vodiča nalaze se u homogenome magnetskome polju od \(2\cdot 10^{-6}\,\textrm{T}\). Vodičima teku struje \(10\,\textrm{A}\) u istome smjeru.
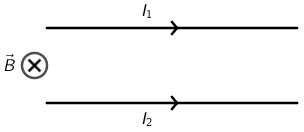
Vodiči se nalaze u ravnini okomitoj na silnice magnetskoga polja i međusobno su udaljeni \(0,2\,\textrm{m}\).
Kolika je ukupna sila na \(1\,\textrm{m}\) duljine vodiča kojim teče struja \(I_{1}\)?
Odgovor: N
Sila kojom magnetsko polje \(\vec{B}\) djeluje na vodič duljine \(\ell\), kojim teče struja \(I\) i koji s magnetskim poljem zatvara kut \(\alpha\): \[F_{\small{\textrm{A}}}=B\,I\,\ell\,\textrm{sin}\, \alpha\]
Sila kojom međusobno djeluju dvije ravne i paralelne strujne žice duljine \(\ell\), kojima teku struje \(I_{1}\) i \(I_{2}\) i nalaze se u vakuumu na udaljenosti \(r\) jednaka je: \[F=\frac{\mu_{0}}{2\pi}\,\frac{I_{1}\,I_{2}\,\ell}{r}=2\cdot 10^{-7}\,I_{1}\,I_{2}\,\frac{\ell}{r}\]
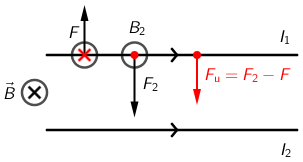
Vodič kojim prolazi struja \(I_{1}\) nalazi se u magnetskom polju vodiča kojim prolazi struja \(I_{2}\) pa na njega struja \(I_{2}\) djeluje silom: \[F_{2}=B_{2}\,I_{1}\ell\] Njezin smjer odredimo pravilom desne ruke pa vidimo da sila ima smjer prema dolje. Budući da je magnetsko polje \(B_{2}\) jednako: \[B_{2}=\frac{\mu_{0}\,\mu_{r}}{2\,\pi}\frac{I}{r}=10^{-5}\,\textrm{T}\] Za silu dobijemo \[F_{2}=10^{-4}\,\textrm{N}\] Taj se vodič nalazi u vanjskom magnetskom polju \(B\) pa na njega djeluje i sila: \[F=B\,I_{1}\ell=2\cdot 10^{-5}\,\textrm{N}\] koja ima smjer prema gore. Ukupna sila koja djeluje na struju \(I_{1}\) jednaka je: \[F_{\textrm{u}}=F_{2}-F=8\cdot 10^{-5}\,\textrm{N}\]
34. zadatak
Duljina neopterećene elastične opruge je 0,15 m. Na oprugu ovjesimo uteg mase 0,1 kg i
zatitramo. Period harmonijskoga titranja utega na opruzi iznosi 0,5 s.
Kolika će biti duljina opruge opterećene tim utegom nakon što titranje prestane?
Odgovor: m

Jednadžba elongacije harmonijskog titranja:
\[y=y_{0}^{\,}\,\textrm{sin}\,\left(\omega\,t+\varphi_{0}\right)\]
Jednadžba brzine harmonijskog titranja:
\[v=\omega\,y_{0}^{\,}\,\textrm{cos}\,\left(\omega\,t+\varphi_{0}\right)\]
Napomena
Na crtežu je graf elongacije označen crvenom, a graf brzine plavom bojom.
Početna faza je:
\[\varphi_{0}^{\,}=\frac{3}{2}\,\pi\]
35. zadatak
Kugla temperature \(200\,^0\textrm{C}\) i površine \(2\cdot 10^{-4}\,\textrm{m}^{2}\) zrači kao crno tijelo.
Koliko energije u vremenu od 60 sekundi kugla izrači u okolinu uz pretpostavku da joj se temperatura pri zračenju ne mijenja?
Odgovor: J
Pomoć potražite na poveznici Stefan-Boltzmannov zakon.
Prema Stefan-Boltzmannovom zakonu, snaga zračenja crnoga tijela jednaka je: \[P=\sigma\cdot S\cdot T^{4}\] Snaga je definirana kao energija u jedinici vremena: \[P=\frac{E}{t}\] Prema tome, energija je jednaka: \[E=\sigma\cdot S\cdot t\cdot T^{4}=34\,\textrm{J}\]