Ljetni rok 2019. godine
1. zadatak
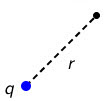
Na slici je prikazan biciklist koji se giba po kružnoj stazi polumjera zakrivljenosti \(r\).
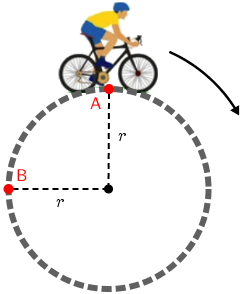
Koliki je iznos pomaka koji je napravio biciklist gibajući se iz točke A u točku B?
- A. \(r\,\pi/2\)
- B. \(3\,r\,\pi/2\)
- C. \(r\,\sqrt{2}\)
- D. \(2\,r\)
Položaj točke u ravnini određujemo pomoću radijus-vektora. Vektor pomaka \(\Delta \vec{r}\) u ravnini, jednak je razlici radijus-vektora krajnjeg i početnog položaja točke.
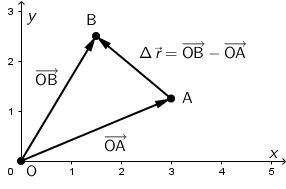
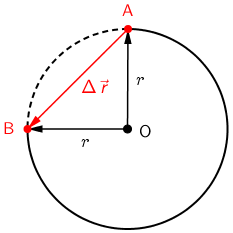
Iz crteža je vidljivo da je vektor pomaka jednak: \[\Delta \vec{r}=\overrightarrow{OB}-\overrightarrow{OA}\] Iznos vektora pomaka odredimo pomoću Pitagorinog poučka: \[\left |\Delta \vec{r}\right |=\sqrt{r^{2}+r^{2}}=r\,\sqrt{2}\]
2. zadatak
Na horizontalnoj podlozi nalaze se dva tijela masa \(m_{1} > m_{2}\) međusobno povezana nerastezljivom niti kao što je prikazano na slici.

Kolika je napetost niti \(N\) koja povezuje tijela ako na tijelo manje mase djeluje stalna sila \(F\) i ako se tijela gibaju ubrzanjem \(a\)?
- A. \(N=m_{2}\,a\)
- B. \(N=m_{2}\,a+F\)
- C. \(N=m_{1}\,a\)
- D. \(N=F-m_{1}\,a\)
Odredite sve sile koje djeluju na tijelo mase \(m_{1}\) pa primijenite temeljni zakon gibanja. To isto napravite i za tijelo mase \(m_{2}\). Iz dobivenih jednadžbi odredite napetost niti \(N\).

Rezultantnu silu na tijelo mase \(m_{2}\) izjednačimo, prema temeljnom zakonu gibanja, s umnoškom mase toga tijela i akceleracije: \[F-N=m_{2}\,a\] Napetost niti je: \[N=F-m_{2}\,a\] Taj odgovor nije ponuđen kao rješenje Na tijelo mase \(m_{1}\) djeluje samo napetost niti: \[N=m_{1}\,a\] To je ujedno i ponuđen odgovor (C).
3. zadatak
Tijelo mase \(m\) giba se po horizontalnoj podlozi stalnom brzinom \(v\) bez trenja. Nakon toga nailazi na hrapavu podlogu takvu da je koeficijent trenja
između tijela i podloge \(\mu\).
Koliki je ukupni put prešlo tijelo po hrapavoj podlozi prije nego što se zbog trenja zaustavilo?
- A. \(\frac{2\,v^{2}}{\mu\, g}\)
- B. \(\frac{v^{2}}{2\,\mu\, g}\)
- C. \(\frac{\mu\, v^{2}}{2\,g}\)
- D. \(2\,\mu\, g\,v^{2}\)
Tijelo se zaustavlja zbog djelovanja sile trenja. Primjenom temeljnog zakona gibanja odredite akceleraciju tijela, a zatim i prijeđeni put tijekom zaustavljanja.
Sila trenja zaustavlja tijelo na hrapavoj podlozi pa je akceleracija tijela: \[a=\frac{F_{\textrm{tr}}}{m}=\frac{\mu\,m\,g}{m}=\mu\,g\] Za vrijeme zaustavljanja gibanje je jednoliko usporeno pa se brzina \(v_{1}\) smanjuje prema izrazu: \[v_{1}^{2}=v^{2}-2\,a\,s\] Kada se tijelo zaustavi, brzina mu je \(v_{1}=0\). Prijeđeni put je: \[s=\frac{v^2}{2\,a}=\frac{v^{2}}{2\,\mu\, g}\]
4. zadatak
Dva satelita masa \(m_{1}=2\,m_{2}\) gibaju se oko Zemlje po kružnim putanjama jednakih polumjera \(r_{1}=r_{2}\).
Koja od navedenih tvrdnja ne vrijedi za gibanje satelita?
- A. Na satelite djeluju jednake centripetalne sile.
- B. Sateliti imaju jednaka ophodna vremena.
- C. Sateliti se gibaju jednakim brzinama.
- D. Sateliti se gibaju jednakim centripetalnim ubrzanjima.
Kako nazivamo silu zbog koje se tijelo giba jednoliko po kružnici? Kojim se izrazom ta sila prikazuje?
Satelit se giba po kružnici zbog djelovanja gravitacijske sile Zemlje mase \(M\) koja ima ulogu centripetalne sile:
\[F_{\textrm{c}}=G\frac{m\,M}{r^{2}}\]
Centripetalnu silu prikazujemo izrazom:
\[F_{\textrm{c}}=\frac{m\,v^{2}}{r}\qquad (1)\]
\[\frac{m\,v^{2}}{r}=G\frac{m\,M}{r^{2}}\qquad (2)\]
Iz izraza (2) zaključujemo da je brzina satelita po kružnoj putanji jednaka:
\[v=\sqrt{G\frac{M}{r}}\qquad(3)\]
Iz izraza (3) zaključujemo da će se oba satelita gibati jednakom brzinom jer su im polumjeri kružnih putanja jednaki.
Budući da su polumjeri kružnih staza oba satelita jednaki, a također i njihove brzine, na osnovu izraza (1) zaključujemo da će na satelit veće mase
djelovati veća centripetalna sila. Prema tome, tvrdnja A ne vrijedi.
5. zadatak
Tijela A i B uronjena su u potpunosti u tekućinu gustoće \(\rho\). Za mase tijela vrijedi \(m_{\textrm{a}}^{\,}=2\,m_{\textrm{b}}^{\,}\),
a za njihove gustoće vrijedi \(\rho_{\textrm{a}}^{\,}=\rho_{\textrm{b}}^{\,}/3\).
Kako se odnose sile uzgona \(F_{\textrm{ua}}\) i \(F_{\textrm{ub}}\) na ta dva tijela?
- A. \(\large\frac{F_{\textrm{ua}}}{F_{\textrm{ub}}}=\frac{2}{3}\)
- B. \(\large\frac{F_{\textrm{ua}}}{F_{\textrm{ub}}}=\normalsize 1\)
- C. \(\large\frac{F_{\textrm{ua}}}{F_{\textrm{ub}}}=\frac{3}{2}\)
- D. \(\large\frac{F_{\textrm{ua}}}{F_{\textrm{ub}}}=\normalsize 6\)
Pomoć potražite na poveznici Sila na uronjeno tijelo-uzgon.
Uzgon na tijelo uronjeno u tekućinu gustoće \(\rho\): \[F_{\textrm{u}}=\rho\, g\,V\] Volumen tijela izrazimo pomoću njegove gustoće \(\rho_{\textrm{tijela}}\) i mase \(m\): \[V=\frac{m}{\rho_{\textrm{tijela}}}\] Uzevši u obzir ovaj izraz, uzgon na tijelo možemo prikazati: \[F_{\textrm{u}}=\rho\, g\,\frac{m}{\rho_{\textrm{tijela}}}\] Masa tijela A dva puta je veća od mase tijela B, dok mu je gustoća tri puta manja od gustoće tijela B. Zbog toga će uzgon na tijelo A biti \[\frac{2}{\frac{1}{3}}=6\,\textrm{puta veći od uzgona na tijelo B.}\] U nastavku možete vidjeti detaljno raspisano rješenje zadatka.
Uzgon na tijelo uronjeno u tekućinu: \[F_{\textrm{u}}=\rho\, g\,V\] Volumene tijela prikažimo pomoću masa: \[V_{a}=\frac{m_{\textrm{a}}^{\,}}{\rho_{\textrm{a}}^{\,}};V_{b}=\frac{m_{\textrm{b}}^{\,}}{\rho_{\textrm{b}}^{\,}}\] Sile uzgona koje djeluju na tijela A i B iznose: \[F_{\textrm{ua}}=\rho\, g\,\frac{m_{\textrm{a}}^{\,}}{\rho_{\textrm{a}}^{\,}};F_{\textrm{ub}}=\rho\, g\,\frac{m_{\textrm{b}}^{\,}}{\rho_{\textrm{b}}^{\,}}\] \[\frac{F_{\textrm{ua}}}{F_{\textrm{ub}}}=\rho\, g\,\frac{m_{\textrm{a}}^{\,}}{\rho_{\textrm{a}}^{\,}}\cdot\frac{\rho_{\textrm{b}}^{\,}}{m_{\textrm{b}}^{\,}\,\rho\, g}= \frac{\rho_{\textrm{b}}^{\,}}{\rho_{\textrm{a}}^{\,}}\cdot\frac{m_{\textrm{a}}^{\,}}{m_{\textrm{b}}^{\,}}=3\cdot 2=6\]
6. zadatak
U posudi se nalazi idealni plin na temperaturi \(0^{\, 0}\textrm{C}\) i atmosferskome tlaku \(p_{0}^{\,}\).
Na koju temperaturu treba izohorno zagrijati plin kako bi tlak u posudi bio \(3\,p_{0}^{\,}\)?
- A. \(273\,\textrm{K}\)
- B. \(273^{\,0}\textrm{C}\)
- C. \(546\,\textrm{K}\)
- D. \(546^{\,0}\textrm{C}\)
Izohornu promjenu stanja plina (promjena stanja plina pri kojoj je volumen plina konstantan), opisujemo jednadžbom: \[\frac{p}{T}=\textrm{konst.}\] Omjer tlaka i termodinamičke temperature je konstantan pa ovu jednadžbu zapisujemo i kao: \[\frac{p_{1}^{\,}}{T_{1}}=\frac{p_{2}^{\,}}{T_{2}}\]
Izohorna promjena stanja plina: \[\frac{p_{0}^{\,}}{T_0}=\frac{p}{T}\] \[T=\frac{p\,T_{0}}{p_{0}^{\,}}=\frac{3\,p_{0}^{\,}}{p_{0}^{\,}}T_{0}=819\, \textrm{K}=546^{\,0}\textrm{C}\]
7. zadatak
Idealni plin obavi rad \(W\) tijekom izobarnoga procesa u kojemu mu se volumen poveća s \(V\) na \(3\,V\).
Koliki dodatni rad obavi idealni plin za daljnje izobarno povećanje volumena s \(3\,V\) na \(6\,V\)?
- A. W
- B. 1,5 W
- C. 2 W
- D. 3 W
Rad plina pri izobarnom procesu (tlak plina je konstantan) prikazujemo izrazom: \[W=p\,\left (V_{2}-V_{1}\right )\] ili \[W=p\,\Delta V\] \(V_{1}\) je volumen plina u početnom stanju, a \(V_{2}\) volumen plina u konačnom stanju.
\[W=p\,\left (V_{2}-V_{1}\right )=p\,\left (3\,V-V\right )=2\,p\,V\] \[W_{1}=p\,\left (V_{2}-V_{1}\right )=p\,\left (6\,V-3\,V\right )=3\,p\,V\] \[\frac{W_{1}}{W}=\frac{3\,p\,V}{2\,p\,V}=\frac{3}{2}\Rightarrow\ W_{1}=1,5\,W\]
8. zadatak
Na slici je prikazan fazni dijagram koji opisuje promjene agregacijskih stanja vode kada joj se stalno dovodi neka količina topline. Početna je temperatura leda je \(-10\,^{0}\textrm{C}\).
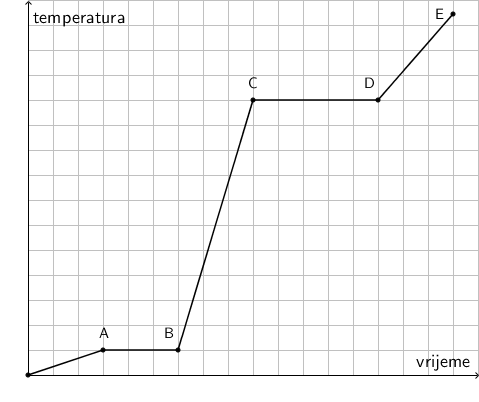
Kolika je temperatura \(t\) u točki C?
- A. \(t=0^{\, 0}\textrm{C}\)
- B. \(0^{\, 0}\textrm{C} < t < 100^{\, 0}\textrm{C}\)
- C. \(t=100^{\, 0}\textrm{C}\)
- D. \(t > 100^{\, 0}\textrm{C}\)
Pomoć potražite na poveznici Promjena agregacijskih stanja.
Iz dijagrama prijelaza zaključujemo da točki A odgovara temperatura \(0^{\, 0}\textrm{C}\) (talište leda), a točki C temperatura \(100^{\, 0}\textrm{C}\) (vrelište vode).
9. zadatak
Koja je od navedenih tvrdnja u skladu sa zakonima termodinamike?
- A. Toplina nekad spontano prelazi s tijela niže na tijelo više temperature.
- B. Moguć je perpetuum mobile druge vrste.
- C. Postoji toplinski stroj bez hladnoga spremnika.
- D. Ne postoji toplinski stroj koji svu toplinu iz toplijega spremnika pretvara u rad.
Pomoć potražite na poveznici Drugi zakon termodinamike.
Od ponuđenih tvrdnji točna je samo ova:
Ne postoji toplinski stroj koji svu toplinu iz toplijega spremnika pretvara u rad.
10. zadatak
Četiri jednaka točkasta naboja nalaze se u vrhovima kvadrata stranice \(a\). Sila između dvaju susjednih naboja jest \(F\).
Kolika je ukupna sila na pojedini naboj?
- A. \(1,41\,F\)
- B. \(1,91\,F\)
- C. \(2,12\,F\)
- D. \(2,41\,F\)
Na naboj u svakom vrhu kvadrata djeluju tri sile. Svaku od tih sila određujemo Coulombovim zakonom: \[F=k\frac{q_{1}\,q_{2}}{r^{2}}=k\frac{q^{2}}{r^{2}}\]
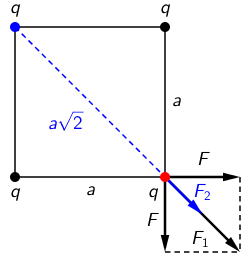
Na naboj označen crvenim kružićem djeluju naboji označeni crnim kružićem silom \(F\): \[F=k\frac{q^{2}}{a^{2}}\] Rezultanta te dvije sile je \(F_{1}\): \[F_{1}=\sqrt{F^{2}+F^{2}}=F\sqrt{2}\] Na taj naboj djeluje još i naboj označen plavim kružićem silom \(F_{2}\): \[F_{2}=k\frac{q^{2}}{\left(a\sqrt{2}\right)^{2}}=k\frac{q^{2}}{2\,a\,^{2}}=\frac{1}{2}F\] Ukupna sila na naboj označen crvenim kružićem je: \[F_{\textrm{R}}=F_{1}+F_{2}=F\left (\sqrt{2}+0,5\right)=1,91\,F\]
11. zadatak
Ekvivalentni otpor četiriju jednakih serijski spojenih otpornika iznosi \(R\).
Koliki će biti ekvivalentni otpor sklopa ako iste otpornike spojimo paralelno?
- A. \(\Large\frac{R}{16}\)
- \(\\\)
- B. \(\Large\frac{R}{4}\)
- C. \(\normalsize 4\,R\)
- D. \(16\,R\)
Pomoć potražite na poveznici Spajanje otpornika.
Ukupni otpor četiri serijski spojena otpora \(R_{0}\) iznosi \(R\): \[R=R_{0}+R_{0}+R_{0}+R_{0}\] Odredimo otpor \(R_{0}\): \[R_{0}=\frac{R}{4}\] Ako te otpore spojimo paralelno, ukupni će otpor biti: \[\frac{1}{R_{\textrm{p}}}=\frac{1}{R_{0}}+\frac{1}{R_{0}}+\frac{1}{R_{0}}+\frac{1}{R_{0}}\] \[\frac{1}{R_{\textrm{p}}}=\frac{4}{R}+\frac{4}{R}+\frac{4}{R}+\frac{4}{R}=\frac{16}{R}\] \[R_{\textrm{p}}=\frac{R}{16}\]
12. zadatak
Kondenzator kapacitivnoga otpora 100 Ω nalazi se u krugu izmjenične struje frekvencije 50 Hz.
Koliki je kapacitet kondenzatora?
- A. 0,32 F
- B. 32 mF
- C. 32 μF
- D. 32 nF
Kapacitivni otpor kondenzatora: \[R_{\small{\textrm{C}}}=\frac{1}{C\,\omega}\] Kružna frekvencija \(\omega\): \[\omega=2\,\pi\,f\]
\[R_{\small{\textrm{C}}}=\frac{1}{C\,\omega}=\frac{1}{2\,\pi\, f}=32\, \mu \textrm{F}\] \[C=\frac{1}{\omega\, R_{\small{\textrm{C}}}}=\frac{1}{2\,\pi\, f\,R_{\small{\textrm{C}}}}=32\, \mu \textrm{F}\]
13. zadatak
Na slici su prikazane ekvipotencijalne linije električnoga polja negativnoga naboja. Probni naboj \(q\) premješta se između dviju od prikazanih točaka A, B, C i D.
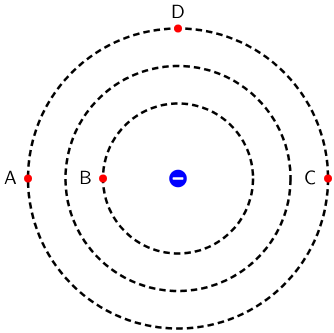
Koja od navedenih jednakosti vrijedi za odnos iznosa obavljenih radova pri premještanju probnoga naboja?
- A. WAB=WBD
- B. WBC=WAC
- C. WAB=WAC
- D. WBC=WCD
Električna potencijalna energija, potencijal i napon
Električna potencijalna energija dva točkasta naboja \(q\) i \(q'\), koji su udaljeni \(r\) jedan od drugog, iznosi: \[E_{\textrm{ep}}=k\frac{q\,q'}{r}\]
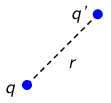
Promjena električne potencijalne energije pri gibanju naboja \(q'\) iz točke A u točku B jednaka je negativnom radu električne sile koja pri tom gibanju djeluje na naboj \(q'\): \[\Delta E_{\textrm{ep}}=-W\]
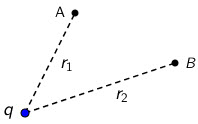
Slika 1.
Taj je rad jednak: \[W=-\left ( E_{\textrm{ep,B}}-E_{\textrm{ep,A}} \right )\] \[W=\left ( E_{\textrm{ep,A}}-E_{\textrm{ep,B}} \right )\] \[W=k\frac{q\,q'}{r_{1}}-k\frac{q\,q'}{r_{2}}\qquad(1)\]
Električni potencijal u nekoj točki električnog polja jednak je električnoj potencijalnoj energiji jediničnog naboja u toj točki: \[\varphi=\frac{E_{\textrm{ep}}}{q'}\] \[\varphi=k\frac{q}{r}\]
Rad električne sile, uzevši u obzir izraz (1), možemo prikazati i pomoću potencijala: \[W=q'\left (\varphi_{\textrm{A}}-\varphi_{\textrm{B}}\right )\] Razliku potencijala između točaka A i B zovemo napon, kojeg označujemo s \(U\) (Slika 1.): \[U=\varphi_{\textrm{A}}-\varphi_{\textrm{B}}\] Rad kojega obavi električno polje pri premještanju naboja \(q'\) iz točke A u točku B prikazujemo i pomoću napona između točaka A i B (Slika 1.): \[W=q'\,U\]
Pretpostavimo da su naboji \(q\) i \(q'\) pozitivni. Koliki rad obavi vanjska sila pri premještanju naboja \(q'\) iz točke A u točku B (Slika 1.)? Taj je rad jednak promjeni električne potencijalne energije: \[W=\left ( E_{\textrm{ep,B}}-E_{\textrm{ep,A}} \right )\] \[W=k\frac{q\,q'}{r_{2}}-k\frac{q\,q'}{r_{1}}\] Taj rad prikazujemo i pomoću potencijala: \[W=q'\left (\varphi_{\textrm{B}}-\varphi_{\textrm{A}}\right )\]
Napomena
Potencijal je skalarna veličina pa može biti pozitivan ili negativan pa pri računanju moramo uzeti u obzir i predznak naboja. Isto vrijedi i za
električnu potencijalnu energiju.
Ekvipotencijalne linije su linije na kojima svaka točka ima jednak potencijal. Potencijal točkastog naboja jednak je: \[\varphi=k\frac{q_{\textrm{i}}^{\,}}{r^2}\] Rad kojega je potrebno izvršiti za premještanje probnog naboja \(q\) iz jedne točke u drugu jednak je: \[W=q\left(\varphi_{2}-\varphi_{1}\right)\]
- \(W_{\textrm{AB}}=q\left(\varphi_{\small{\textrm{B}}}-\varphi_{\small{\textrm{A}}}\right)\)
- \(W_{\textrm{BD}}=q\left(\varphi_{\small{\textrm{D}}}-\varphi_{\small{\textrm{B}}}\right)\)
- \(W_{\textrm{BC}}=q\left(\varphi_{\small{\textrm{C}}}-\varphi_{\small{\textrm{B}}}\right)\)
- \(W_{\textrm{AC}}=0\)
- \(W_{\textrm{CD}}=0\)
14. zadatak
Na slici je prikazan dio dugoga ravnog vodiča kojim prolazi električna struja \(I\).
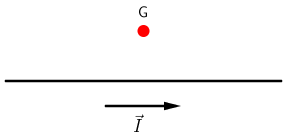
Koja je orijentacija vektora magnetske indukcije \(\vec{B}\) u točki G?
- A. prema dolje \(\downarrow\)
- B. iz ravnine papira \(\odot\)
- C. prema gore \(\uparrow\)
- D. u ravninu papira \(\otimes\)
Mikrovalovi su elektromagnetski valovi valnih duljina između 1 mm i 1 m.
Primjenom pravila desne ruke zaključujemo da je magnetsko polje orijentirano iz ravnine papira.
15. zadatak
Harmonijski oscilator sastoji se od utega pričvršćenoga na oprugu koji neprigušeno titra. Početna energija oscilatora iznosi 10 J. Kolika je elastična potencijalna energija sustava kada uteg prolazi kroz ravnotežni
- A. -10 J
- B. 0 J
- C. 5 J
- D. 10 J
Pomoć potražite na poveznici Harmonijsko titranje-pretvorbe energije.
Elastična potencijalna energija harmonijskog oscilatora: \[E_{\textrm{pe}}=\frac{1}{2}k\,x^{2}\] U ravnotežnom položaju elongacija je \(x=0\) pa je i \(E_{\textrm{pe}}=0\).
16. zadatak
Zadana je jednadžba vala \[y=10\, \textrm{cm sin}\,\left(\frac{\pi\, t}{4\,\textrm{s}}-\frac{2\, \pi\, x}{24\, \textrm{m}}\right)\] Kolika je brzina širenja toga vala?
- A. 3 m/s
- B. 6 m/s
- C. 10 m/s
- D. 12 m/s
Pomoć potražite na poveznici Jednadžba vala.
Uspoređivanjem jednadžbe harmonijskog vala \[y=A\ \textrm{sin}\,\left(\frac{2\,\pi}{T}t-\frac{2\,\pi}{\lambda}\,x\right)\] sa zadanom jednadžbom, zaključujemo: \[\frac{2\,\pi}{T}=\frac{\pi}{4}\Rightarrow\ T=8\, \textrm{s}\] \[\frac{2\,\pi}{\lambda}=\frac{2\,\pi}{24}\Rightarrow\lambda=24\, \textrm{m}\] Brzina širenja vala je: \[v=\frac{\lambda}{T}=3\, \textrm{m}/\textrm{s}\]
17. zadatak
U baterijskoj svjetiljci upotrebljava se konkavno zrcalo.
Gdje u svjetiljci treba postaviti žaruljicu kako bi nastao paralelan snop svjetlosti?
- A. u tjeme zrcala
- B. u žarište zrcala
- C. u centar zakrivljenosti zrcala
- D. u točku koja se nalazi na polovini žarišne daljine zrcala
Pomoć potražite na poveznici Jednadžba konkavnog zrcala.
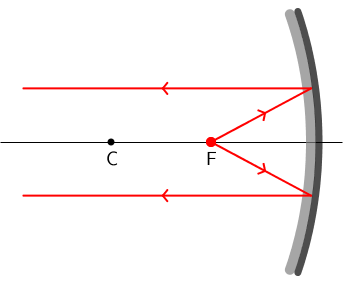
Ako u žarište konkavnog zrcala postavimo žaruljicu, sve zrake svjetlosti koje izlaze iz žaruljice nakon refleksije na zrcalu bit će paralelne optičkoj osi zrcala.
18. zadatak
Učenik izvodi pokus puštajući laserski snop svjetlosti frekvencije f na dvije vrlo uske pukotine razmaknute za
d. Na zastoru udaljenome a od pukotina opaža svijetle pruge razmaknute za s.
Učenik uzima drugi laser čija je frekvencija svjetlosti
f1=1,5 f.
Koliki razmak s1 opaža učenik između svijetlih pruga na zastoru nakon
što osvijetli pukotine drugim laserom?
- A. s1 = s/2
- B. s1 = 2 s/3
- C. s1 = s
- D. s1 = 3 s/2
Pomoć potražite na poveznici Youngov pokus.
Udaljenost između susjednih pruga interferencije: \[s=\frac{\lambda\, a}{d}\] Valnu duljinu svjetlosti možemo prikazati i pomoću frekvencije: \[\lambda=\frac{c}{f}\] \[s=\frac{c\, a}{f\,d}\] Kada učenik uzme laser frekvencije f1=1,5 f udaljenost između susjednih pruga biti će: \[s_{1}=\frac{c\,a}{1,5\,f\,d}=\frac{2}{3}\cdot \frac{c\, a}{f\,d}=\frac{2}{3}\,s\]
19. zadatak
Jedna leća ima jakost \(j_{1}=1\, \textrm{m}^{-1}\), a druga \(j_{2}=-1\, \textrm{m}^{-1}\).
Koja je od navedenih tvrdnja točna?
- A. Leća jakosti \(j_{1}\) daje uvijek uvećane slike, a leća jakosti \(j_{2}\) daje uvijek umanjene slike.
- B. Leća jakosti \(j_{1}\) daje uvijek umanjene slike, a leća jakosti \(j_{2}\) daje uvijek uvećane slike.
- C. Leća jakosti \(j_{1}\) daje uvijek uspravne slike, a leća jakosti \(j_{2}\) daje i uspravne i obrnute slike.
- D. Leća jakosti \(j_{1}\) daje i uspravne i obrnute slike, a leća jakosti \(j_{2}\) daje uvijek uspravne slike.
Pomoć potražite na poveznici Sabirne i rastresne leće.
Leća jakosti \(j_{1}=1\, \textrm{m}^{-1}\) ima pozitivnu žarišnu daljinu pa je to konvergentna leća. Konvergentna leća može dati realnu i obrnutu ili virtualnu i uspravnu sliku. Leća jakosti \(j_{2}=-1\, \textrm{m}^{-1}\) ima negativnu žarišnu daljinu pa je to divergentna leća. Divergentna leća uvijek daje virtualnu i uspravnu sliku.
20. zadatak
Što od navedenoga dokazuje da je svjetlost transverzalni val?
- A. ogib svjetlosti
- B. disperzija svjetlosti
- C. polarizacija svjetlosti
- D. interferencija svjetlosti
Pomoć potražite na poveznici Polarizacija svjetlosti
Točan odgovor je C.
21. zadatak
Ako se elektroni u atomima vodika nalaze na energijskoj razini n = 4, koliki je maksimalni broj različitih fotona koji se mogu emitirati pri prijelazu takvih atoma u osnovno stanje ako su svi prijelazi dopušteni?
- A. 1
- B. 4
- C. 6
- D. 8
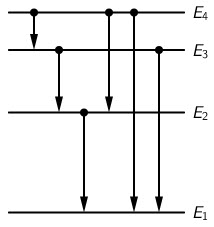
\(E_{4}\rightarrow\ E_{3}\), \(E_{3}\rightarrow\ E_{2}\), \(E_{2}\rightarrow\ E_{1}\), \(E_{4}\rightarrow\ E_{2}\),\(E_{4}\rightarrow\ E_{1}\),
\(E_{3}\rightarrow\ E_{1}\)
Ukupno šest fotona različitih energija.
22. zadatak
Koja od navedenih fizičkih veličina ima jednaki iznos za promatrača na Zemlji i za promatrača u letjelici koja se giba brzinom 0,99 c u odnosu na Zemlju?
- A. brzina svjetlosti
- B. količina gibanja miona
- C. energija miona
- D. srednje vrijeme života miona
Pomoć potražite na poveznici Lorentzove transformacije.
Brzina svjetlosti u svim inercijskim sustavima je konstantna.
23. zadatak
Dva radioaktivna uzorka B i C imaju jednaku početnu aktivnost. Vrijeme poluraspada uzorka B
iznosi šest sati, a uzorka C jedan dan.
Koliki je omjer aktivnosti \(A_{\small{\textrm{B}}}:A_{\small{\textrm{C}}}\) tih dvaju uzoraka nakon dva dana?
- A. \(A_{\small{\textrm{B}}}:A_{\small{\textrm{C}}}=1:64\)
- B. \(A_{\small{\textrm{B}}}:A_{\small{\textrm{C}}}=64:1\)
- C. \(A_{\small{\textrm{B}}}:A_{\small{\textrm{C}}}=1:16\)
- D. \(A_{\small{\textrm{B}}}:A_{\small{\textrm{C}}}=16:1\)
Pomoć potražite na poveznici Zakon radioaltivnog raspada.
Aktivnost se tijekom vremena mijenja kao i broj neraspadnutih jezgara: \[A=A_{0}\cdot 2^{-\frac{t}{T}}\] \[\frac{A_{B}}{A_C}=\frac{A_{0}\cdot 2^{-\frac{48}{6}}}{A_{0}\cdot 2^{-\frac{48}{24}}}=\frac{2^{-8}}{2^{-2}}=\frac{4}{256}=\frac{1}{64}\]
24. zadatak
24. Jedan kamen bačen je vertikalno prema gore s vrha litice brzinom \(v\). Drugi kamen bačen je s iste litice jednakom brzinom \(v\) vertikalno prema dolje.
Koji kamen ima veću brzinu u trenutku udara o tlo? Zanemarite otpor zraka.
- A. Kamen bačen prema gore ima veću brzinu.
- B. Oba kamena imaju jednaku brzinu.
- C. Kamen bačen prema dolje ima veću brzinu.
Primijenite zakon očuvanja mehaničke energije.
U trenutku izbacivanja oba kamena imaju jednaku ukupnu mehaničku energiju: \[E_{1,\textrm{poc}}=E_{2,\textrm{poc}}\] \[E_{1,\textrm{poc}}=m\,g\,h+\frac{m\,v^2}{2}\] \[E_{2,\textrm{poc}}=m\,g\,h+\frac{m\,v^2}{2}\] Zbog očuvanja mehaničke energije, u trenutku pada na tlo ukupna energija im također mora biti jednaka: \[E_{1,\textrm{kon}}=E_{2,\textrm{kon}}\] \[E_{1,\textrm{kon}}=0+\frac{m\,v_{1}^2}{2}=\frac{m\,v_{1}^2}{2}\] \[E_{2,\textrm{kon}}=0+\frac{m\,v_{2}^2}{2}=\frac{m\,v_{2}^2}{2}\] Zato i brzine oba kamena u trenutku pada moraju biti jednake: \[v_{1}^{\,}=v_{2}^{\,}\]
25. zadatak
Struja prolazi kroz dva paralelna beskonačna vodiča u istome smjeru.
Koja je od navedenih tvrdnja točna?
- A. Vodiči ne djeluju jedan na drugoga.
- B. Vodiči se međusobno privlače.
- C. Vodiči se međusobno odbijaju.
Pomoć potražite na poveznici Magnetska sila između dvije paralelne strujne žice.
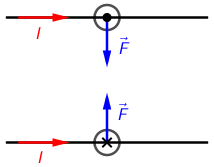
Primijenom pravila desne ruke zaključujemo da se vodiči privlače.
26. zadatak
Akceleracija sile teže na površini Mjeseca šest puta je manja nego na površini
Zemlje.
Ako je masa Mjeseca 7,3·10 22 kg, koliki je polumjer Mjeseca?
Odgovor: m
Pomoć potražite na poveznici: Opći zakon gravitacije.
Akceleracija sile teže na površini Mjeseca: \[g_{\small{\textrm{M}}^{\,}}=G\frac{M}{R^{2}}\] Prema zadatku je: \[g_{\small{\textrm{M}}^{\,}}=\frac{g_{\small{\textrm{Z}}^{\,}}}{6}\] \[G\frac{M}{R^2}=\frac{10}{6}\] \[R=\sqrt{\frac{6\,G\,M}{10}}=1,71\cdot 10^{6}\, \textrm{m}\]
27. zadatak
Idealni plin u zatvorenoj posudi podvrgava se promjenama tijekom termodinamičkoga procesa kao što je prikazano u \(p,V\) grafu.
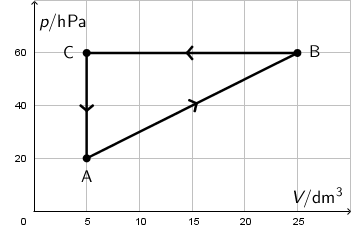
Koliki je rad obavio plin tijekom jednoga procesa A-B-C-A?
Odgovor: J
Pomoć potražite na poveznici: Rad plina u kružnom procesu.
Po iznosu rad plina jednak je površini lika u \(p,V\) grafu. Po predznaku rad je negativan jer se proces odvija u smjeru koji je suprotan smjeru kazaljke na satu (plin obavi manji rad za vrijeme širenja od A do B nego okolina za vrijeme sabijanja od B do C): \[W=-\frac{\overline{\textrm{BC}}\cdot\overline{\textrm{CA}}}{2}=-\frac{20\cdot 10^{-3}\cdot 40\cdot 10^{2}}{2}=-40\, \textrm{J}\]
28. zadatak
Vodič duljine 20 cm nalazi se u magnetskome polju i sa smjerom polja zatvara kut
300.
Kolika je magnetska indukcija ako vodičem prolazi struja 2 A i ako na njega djeluje sila 4 mN?
Odgovor: T
Pomoć potražite na poveznici: Djelovanje magnetskog polja na električnu struju.
Sila kojom magnetsko polje djeluje na vodič kojim teče struja jednaka je: \[F=B\,I\,\ell\, \textrm{sin}\, \alpha\] \[B=\frac{F}{I\,\ell\,\textrm{sin}\,\alpha}=2\,\cdot 10^{-2}\,\textrm{T}=0,02\,\textrm{T}\]
29. zadatak
Kolika je ukupna razina intenziteta zvuka gudačkoga kvarteta ako svaki od četiriju instrumenata daje ton intenziteta \(10^{-6}\, \textrm{W}/\textrm{m}^2\)?
Odgovor: dB
Pomoć potražite na poveznici: Decibelna ljestvica.
Razina intenziteta zvuka: \[L=10\, \textrm{log}\frac{I}{I_{0}}\] Intenzitet četiri gudačka kvarteta bit će četiri puta veći: \[L=10\, \textrm{log}\frac{4\,I}{I_{0}}=66\, \textrm{dB}\]
Napomena
Pragu čujnosti \(I_{0}=10^{\mathbf{-}12}\,\textrm{W}/\textrm{m}^{2}\) odgovara odgovara razina intenziteta 0 dB.
30. zadatak
Vrijeme poluraspada jezgre \({_{\;6}^{11}}\,\textrm{C}\) jest 20,4 min.
Nakon koliko se vremena raspadne 3/4 početnoga broja jezgara?
Odgovor: min
Pomoć potražite na poveznici: Zakon radioaktivnog raspada.
Iz zakona radioaktivnog raspada \[N=N_{0}\cdot 2^{-\frac{t}{T}}\] odredimo broj raspadnutih jezgara: \[\Delta N=N_{0}\,–N\] \[\Delta N=N_{0}\left(1-2^{-\large \frac{t}{T}}\right)\] \[\Delta N=\frac{3}{4}\,N_{0}\] \[N_0\left(1-2^{-\large\frac{t}{T}}\right)=\frac{3}{4}\,N_{0}\] \[t=40,8\, \textrm{min}\]
Napomena
Zadatak se može riješiti brže i lakše. Nakon \(t=T\) raspadne se
\[\Delta N=\frac{1}{2}\,N_{0}\]
a nakon još jednog vremena poluraspada još polovina od preostalog broja jezgara. Ukupno se za dva vremena poluraspada
(\(t=2\cdot 20,4\, \textrm{min}=40,8\, \textrm{min}\)) raspadne
\[\Delta N=\frac{1}{2}\,N_{0}+\frac{1}{4}\,N_{0}=\frac{3}{4}\,N_{0}\]
31. zadatak
Koliki je iznos stalne sile potrebne za ubrzanje automobila mase 1300 kg iz stanja mirovanja do brzine 72 km/h na putu 80 m?
Odgovor: N
Primijenite izraz za brzinu kod jednoliko ubrzanog pravocrtnog gibanja i temeljni zakon gibanja.
Gibanje je jednoliko ubrzano pa iz izraza za brzinu kod jednoliko ubrzanog gibanja \[v^{2}=2\,a\,s\] odredimo akceleraciju: \[a=\frac{v^{2}}{2\,s}\] Primjenom temeljnog zakona gibanja odredimo silu koja je ubrzavala automobil: \[F=m\,a=\frac{m\,v^{2}}{2\,s}=3250\, \textrm{N}\]
32. zadatak
U posudi volumena \(10\, \textrm{cm}^{3}\) nalazi se idealni plin pri tlaku \(10^{3}\, \textrm{Pa}\) i temperaturi \(0\,^{0}\textrm{C}\).
Koliki je broj molekula plina u posudi?
Odgovor:
Pomoć potražite na poveznici: Jednadžba stanja idealnog plina.
Iz jednadžbe stanja idealnog plina \[p\,V=N\,k\,T\] odredimo broj molekula plina: \[N=\frac{p\,V}{k\,T}=2,65\cdot 10^{18}\]
33. zadatak
Koliko iznosi ekvivalentni otpor spoja prikazanoga na slici između točaka A i B?
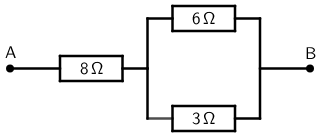
Odgovor: \(\Omega\)
Pomoć potražite na poveznici: Spajanje otpornika.
Odredimo otpor paralelno spojenih otpornika: \[\frac{1}{R_{\textrm{p}}}=\frac{1}{6}+\frac{1}{3}\Rightarrow R_{\textrm{p}}=2\, \Omega\] Ukupan otpor između točaka A i B je: \[R=8+2=10\, \Omega\]
34. zadatak
Tijelo A mase 5 kg miruje na stolu i povezano je nerastezljivom niti preko koloture s
tijelom B mase 3 kg kao što je prikazano na slici. Koeficijent trenja između tijela
A i podloge jest 0,2. Sustav pustimo da se giba iz stanja mirovanja.
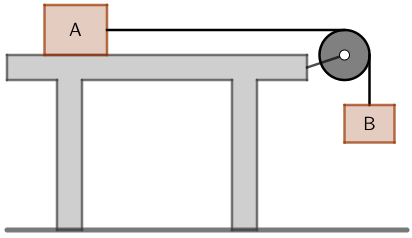
Koliku brzinu ima tijelo B nakon 0,5 s gibanja?
Zanemarite masu niti i trenje između niti i koloture.
Odgovor: m/s
Odredite rezultantu svih sila koje djeluju na tijelo B i primijenite temeljni zakon gibanja kako biste odredili akceleraciju tijela
B.
Postupak ponovite i za tijelo A.
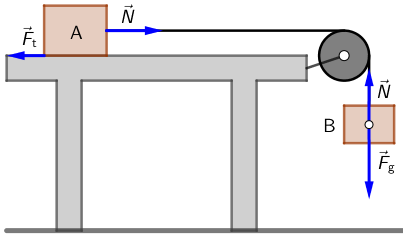
Na tijelo B djeluje sila teža \(F_{\textrm{g}}\) prema dolje i napetost niti \(N\) prema gore. Rezultanta tih sila ubrzava tijelo B: \[F_{\textrm{g}}-N=m_{\small{\textrm{B}}}\,a\] Na tijelo A djeluju napetost niti \(N\) prema desno i sila trenja \(F_{\textrm{tr}}\) prema lijevo. Rezultanta tih sila ubrzava tijelo A: \[N-F_{\textrm{tr}}=m_{\small{\textrm{A}}}\,a\] (Budući da je nit nerastezljiva, oba se tijela gibaju jednakom akceleracijom.) Zbrojimo prethodne jednadžbe i uvrstimo izraze za silu težu koja djeluje na tijelo B i silu trenja koja djeluje na tijelo A: \[m_{\small{\textrm{B}}}\,g-\mu\,m_{\small{\textrm{A}}}\,g=a\left(m_{\small{\textrm{A}}}+m_{\small{\textrm{B}}}\right)\] Akceleracija kojom se giba tijelo B (i tijelo A) jednaka je: \[a=\frac{m_{\small{\textrm{B}}}-\mu\,m_{\small{\textrm{A}}}}{m_{\small{\textrm{A}}}+m_{\small{\textrm{B}}}}\,g=2,5\, \frac{\textrm{m}}{\textrm{s}^{2}}\] Brzina tijela B nakon 0,5 s iznosi: \[v=a\,t=1,25\, \textrm{m}/\textrm{s}\]
35. zadatak
Ploče kondenzatora međusobno su udaljene 2 cm i priključene na napon
2·103 V. Između ploča kondenzatora homogeno električno polje usmjereno je vertikalno prema gore.
U tome polju u zraku lebdi kapljica ulja mase 3 μg.
Koliki je njezin naboj?
Odgovor: C
Koje sile djeluju na kapljicu ulja? Koliki mora biti njihov iznos, a kakva im je orijentacija?
Je li kapljica nabijena pozitivnim ili negativnim nabojem?
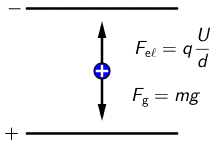
Pozitivno nabijena kapljica ulja će lebdjeti ako je iznos električne sile jednak iznosu sile teže i ako su te sile suprotno orijentirane: \[F_{\textrm{e}}=F_{\textrm{g}}\] \[F_{\textrm{e}}=q\,E=q\,\frac{U}{d}\] \[q\,\frac{U}{d}=m\,g\] \[q=\frac{m\,g\,d}{U}=3\cdot 10^{\mathbf{-}13}\, \textrm{C}\]
36. zadatak
Tijelo mase 1 kg harmonijski titra. Ovisnost ubrzanja tijela o vremenu dana je jednadžbom: \[a=\left(24\, \textrm{ms}^{-2}\right)\, \textrm{sin}\, \left(4\, \textrm{s}^{-1}\,t\right)\] Kolika je kinetička energija tijela u trenutku kada mu je elongacija 0,75 m?
Odgovor: J
Kojom jednadžbom prikazujemo akceleraciju harmonijskog titranja, a kojom elongaciju?
Akceleraciju harmonijskog titranja opisujemo jednadžbom: \[a=-A\,\omega^{2}\,\textrm{sin}\, \omega\, t\] Usporedbom jednadžbe za akceleraciju i zadane jednadžbe \[a=\left(24\, \textrm{ms}^{-2}\right)\, \textrm{sin}\, \left(4\, \textrm{s}^{-1}\,t\right)\] zaključujemo: \[\omega=4\, \textrm{s}^{-1}\] \[-A\,\omega^{2}=24 \Rightarrow A=-\frac{24}{4^{2}}=-1,5\, \textrm{m}\] Harmonijska konstanta jednaka je: \[k=m\,\omega^{2}\] Ukupna energija harmonijskog titranja jednaka je maksimalnoj elastičnoj potencijalnoj energiji: \[E=\frac{1}{2}\,k\,A^{2}=\frac{1}{2}\,m\,\omega^{2}\,A^{2}\] U trenutku kada je elongacija jednaka \(x=0,75\, \textrm{m}\) elastična potencijalna energija je \[E_{\textrm{p}}=\frac{1}{2}\,k\,x^{2}=\frac{1}{2}\,m\,\omega^{2}\,x^{2}\] Iz zakona očuvanja energije \[E=E_{\textrm{p}}+E_{\textrm{k}}\] odredimo kinetičku energiju: \[E_{\textrm{k}}=E-E_{\textrm{p}}\] \[E_{\textrm{k}}=\frac{1}{2}\,m\,\omega^{2}\,A^{2}-\frac{1}{2}\,m\,\omega^{2}\,x^{2}=\frac{1}{2}\,m\,\omega^{2}\left(A^{2}-x^{2}\right)\] \[E_{\textrm{k}}=\frac{1}{2}\,m\,\omega^{2}\left(A^{2}-x^{2}\right)\] \[E_{\textrm{k}}=8\cdot\left(2,25-0,5625\right)=8\cdot 1,6875=13,5\, \textrm{J}\]
37. zadatak
Natrijevu pločicu obasjamo elektromagnetskim zračenjem frekvencije 7,5·1014 Hz.
Najveća valna duljina koja izaziva fotoelektrični učinak kod natrija jest 530 nm.
Kolika je de Broglieva valna duljina emitiranih elektrona pri napuštanju natrija?
Odgovor: m
Pomoć potražite na poveznicama:
Iz granične valne duljine za natrij odredimo izlazni rad natrija: \[W_{0}=h\frac{c}{\lambda_{\textrm{g}}}=3,75\cdot 10^{-19}\, \textrm{J}\] Primijenimo Einsteinovu jednadžbu fotoelektričnog učinka: \[E_{\textrm{f}}=W_{0}+E_{\textrm{k}}\] Najveća kinetička energija izbačenih elektrona je: \[E_{\textrm{k}}=E_{\textrm{f}}-W_{0}=hf-W_{0}=1,22\cdot 10^{-19}\, \textrm{J}\] De Broglieva valna duljina elektrona je: \[\lambda=\frac{h}{p}\] Impuls elektrona prikažimo pomoću kinetičke energije: \[E_{\textrm{k}}=\frac{m\,v^{2}}{2}=\frac{m^{2}\,v^{2}}{2\,m}=\frac{p^{2}}{2\,m}\] \[p=\sqrt{2\,m\,E_{\textrm{k}}}\] \[\lambda=\frac{h}{p}=\frac{h}{\sqrt{2\,m\,E_{\textrm{k}}}}=1,41\cdot 10^{-9}\, \textrm{m}\]