Ljetni rok 2022. godine
1. zadatak
Na slici je prikazan graf ovisnosti položaja tijela o vremenu.
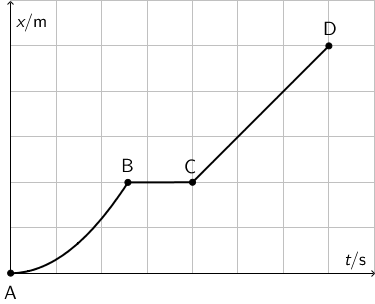
Koji dio grafa prikazuje ubrzano gibanje?
- A. AB
- B. BC
- C. CD
- D. AD
Graf položaja u ovisnosti o vremenu za jednoliko ubrzano gibanje prikazan je parabolom.
Dio grafa AB prikazuje dio parabole.
2. zadatak
Automobil miruje na horizontalnoj cesti.
Koja je od navedenih tvrdnja točna?
- A. Na automobil djeluje samo sila teža.
- B. Na automobil ne djeluje niti jedna sila.
- C. Na automobil djeluje samo reakcija podloge.
- D. Na automobil djeluje više od jedne sile.
Sile koje djeluju na automobil u gibanju prikazane su na crtežu:
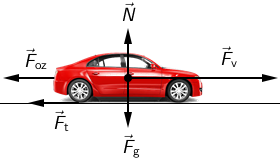
- \(\vec{F}_{\textrm{g}}\) - sila teža
- \(\vec{N}\) - reakcija podloge
- \(\vec{F}_{\textrm{v}}\) - vučna sila motora automobila
- \(\vec{F}_{\textrm{t}}\) - sila trenja
- \(\vec{F}_{\textrm{oz}}\) - sila otpora zraka
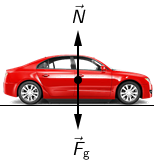
Na automobil u mirovanju djeluju dvije sile: sila teža i reakcija podloge.
3. zadatak
Pretpostavite da se kazaljke sata gibaju kontinuirano.
Koliko iznosi omjer kutnih brzina minutne i satne kazaljke sata?
- A. 1
- B. 6
- C. 12
- D. 72
Ophodno vrijeme minutne kazaljke je 60 min ili 1 h: \[T_{\textrm{min}}= 1\,\textrm{h}\]
Ophodno vrijeme satne kazaljke je 12 h: \[T_{\textrm{h}}= 12\,\textrm{h}\]
Kutna brzina: \[\large\omega=\normalsize\frac{2\,\pi}{T}\] Omjer kutnih brzina minutne i satne kazaljke: \[\frac{\large\omega_{\normalsize\textrm{min}}}{\large\omega_{\normalsize\textrm{h}}}=\frac{2\,\pi}{T_{\textrm{min}}}\cdot \frac{T_{\textrm{h}}}{2\,\pi}\] \[\frac{\large\omega_{\normalsize\textrm{min}}}{\large\omega_{\normalsize\textrm{h}}}=\frac{T_{\textrm{h}}}{T_{\textrm{min}}}=\frac{12\,\textrm{h}}{1\,\textrm{h}}=12\]
4. zadatak
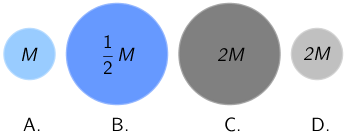
Četiri homogena planeta imaju mase kao što je prikazano na slici.
Koji bi od prikazanih planeta djelovao najvećom gravitacijskom silom na neko tijelo mase m koje se nalazi na površini toga planeta?
- A. Planet A.
- B. Planet B.
- C. Planet C.
- D. Planet D.
Primijenimo Newtonov zakon gravitacije.
Dva tijela, čija su središta udaljena \(r\) i kojima su mase \(m_{1}\) i \(m_{2}\), privlače se gravitacijskom silom \(F\):
\[F=G\,\frac {m_{1}\,m_{2}}{r^{2}}\]
Neka je \(m_{\textrm{p}}\) masa palneta, a masa tijela koje se nalazi na površini toga planeta \(m\). Polumjer planeta označimo s \(R\). Sila kojom planet privlači tijelo na svojoj površini jednaka je: \[F=G\,\frac {m_{\textrm{p}}\,m}{R^{2}}\] Iz ovog izraza zaključujemo da je sila kojom planet privlači tijelo na svojoj površini najveća ako je masa planeta najveća, a polumjer najmanji. Taj je uvjet ispunjen za planet D.
5. zadatak
Dvije metalne tanke žice A i B imaju pri temperaturi 0 oC
istu duljinu \(\ell_{0}\). Žica A zagrije se na 24 oC.
Linearni koeficijent toplinskoga rastezanja žice A je 1,2 puta veći od linearnoga koeficijenta toplinskoga
rastezanja žice B.
Na koliku temperaturu treba zagrijati žicu B da bi se produljila za isti iznos kao i žica A?
- A. na 20,0 oC
- B. na 24,0 oC
- C. na 28,80 oC
- D. na 86,4 oC
Duljina žice pri temperaturi \(t\): \[\ell=\ell_{0}\left ( 1+\alpha\,\Delta t \right )\] Produljene žice zbog zagrijavanja: \[\Delta \ell=\alpha\,\ell_{0}\,\Delta t\]
- \(\ell_{\,0}\) - duljina žice pri početnoj temperaturi \(t_{0}\)
- \(\ell\) - duljina žice pri konačnoj temperaturi \(t\)
- \(\Delta \ell=\ell-\ell_{\,0}\) - produljenje žice zbog zagrijavanja
- \(\Delta t=t-t_{0}\) - promjena temperature
- \(\alpha\)- koeficijent linearnog toplinskog širenja
Prikažimo produljenje žice A i žice B zbog zagrijavanja: \[\Delta \ell_{\textrm{A}}=1,2\,\alpha\,\ell_{0}\,\Delta t_{\textrm{A}}\] \[\Delta \ell_{\textrm{B}}=\alpha\,\ell_{0}\,\Delta t_{\textrm{B}}\] Prema zadatku ta su produljenja jednaka: \[\Delta \ell_{\textrm{B}}=\Delta \ell_{\textrm{A}}\] \[\alpha\,\ell_{0}\,\Delta t_{\textrm{B}}=1,2\,\alpha\,\ell_{0}\,\Delta t_{\textrm{A}}\] \[\Delta t_{\textrm{B}}=1,2\,\Delta t_{\textrm{A}}\] \[\Delta t_{\textrm{B}}=28,8^{\,\textrm{o}}\textrm{C}\]
6. zadatak
U jednoj zatvorenoj posudi nalazi se helij, a u drugoj zatvorenoj posudi argon pri jednakim temperaturama. Pretpostavite da su plinovi idealni. Kakav je odnos srednjih kinetičkih energija atoma navedenih plinova?
- A. Atomi helija imaju približno deset puta veću srednju kinetičku energiju od atoma argona.
- B. Atomi helija imaju jednaku srednju kinetičku energiju kao i atomi argona.
- C. Atomi helija imaju približno deset puta manju srednju kinetičku energiju od atoma argona.
- D. Atomi helija imaju približno sto puta manju srednju kinetičku energiju od atoma argona.
Srednja kinetička energija molekula jednoatomnog idealnog plina ("molekule" se sastoje od jednog atoma): \[\bar{E_{\textrm{k}}}=\frac{3}{2}\,k\,T\] Srednja kinetička energija molekula dvoatomnog idealnog plina pri temperaturama koje nisu previše visoke: \[\bar{E_{\textrm{k}}}=\frac{5}{2}\,k\,T\] Srednja kinetička energija molekula troatomnog idealnog plina pri temperaturama koje nisu previše visoke:: \[\bar{E_{\textrm{k}}}=\frac{6}{2}\,k\,T=3\,k\,T\]
Helij i argon su jednoatomni plinovi, a prema zadatku su i idealni. Srednja kinetička energija jednoatomnog idealnog plina jednaka je: \[\bar{E_{\textrm{k}}}=\frac{3}{2}\,k\,T\] Točan odgovor je B.
7. zadatak
Na slici je prikazan Q, ΔT graf za tri različite tekućine jednakih masa.
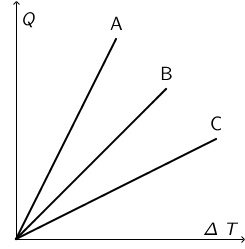
Koji je od navedenih odnosa točan za njihove specifične toplinske kapacitete?
- A. cA < cB <cC
- B. cA<cB >cC
- C. cA>cB >cC
- D. cA>cB <cC
Toplina potrebna za zagrijavanje tekućine: \[Q=m\,c\,\Delta T\]
- \(m\) - masa tekućine
-
\(c\) - specifični toplinski kapacitet tekućine
Toplina potrebna da se jednom kilogramu tekućine ili neke druge tvari temperatura povisi za jedan stupanj. - \(\Delta T\) - porast temperature tekućine ili nekog drugog tijela tijela.
Izraz za količinu topline koju prima tekućina
\[Q=m\,c\,\Delta T\]
podijelimo s \(m\).
\[\frac{Q}{m}=c\,\Delta T\]
Sve tri tekućine imaju jednaku masu pa možemo zaključiti da je toplina koju tekućine primaju proporcionalna promjeni njihove temperature, pri čemu je
koeficijent proporcionalnosti specifični toplinski kapacitet \(c\). Koeficijent proporcionalnosti jednak je nagibu pravca u \(Q, \Delta T\) grafu.
Najveći nagib ima pravac A, a najmanji pravac C. Prema tome, točan je odgovor naveden pod C.
8. zadatak
Hladniji je spremnik Carnotova toplinskoga stroja pri temperaturi T.
Pri kojoj će od navedenih temperatura toplijega spremnika korisnost toga stroja biti najveća?
- A. T/2
- B. T
- C. 2T
- D. 3T
Korisnost Carnotovog toplinskog stroja \(\eta\) \[\eta=\frac{Q_{1}-Q_{2}}{Q_{1}}\] ili \[\eta=\frac{T_{1}-T_{2}}{T_{1}}\] \[\eta=1-\frac{T_{2}}{T_{1}}\]
- \(Q_{1}\) - toplina koju stroj prima od toplijeg spremnika (uložena energija)
- \(T_{1}\) - temperatura toplijeg spremnika
- \(Q_{2}\) - toplina koju stroj predaje hladnijem spremniku
- \(T_{2}\) - temperatura hladnijeg spremnika
- \(W=Q_{1}-Q_{2}\) - Koristan rad kojega obavi stroj
U izraz za korisnost Carnotovog stroja \[\eta=1-\frac{T_{2}}{T_{1}}\] uvrstimo \[T_{2}=T\] \[\eta=1-\frac{T}{T_{1}}\] Korisnost će biti najveća ako je razlomak u prethodnom izrazu najmanji, a on je najmanji ako je nazivnik \(\left(T_{1}\right)\) najveći. Od ponuđenih odgovora za temperaturu toplijeg spremnika najveći je onaj pod D.
9. zadatak
Četiri naboja nalaze se u vrhovima kvadrata stranice duljine d kao što je prikazano na crtežu.
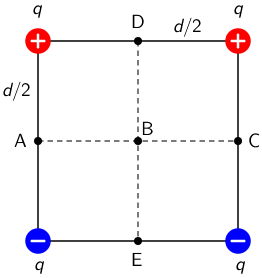
Prema kojoj je točki orijentirano električno polje u točki B?
- A. prema točki D
- B. prema točki C
- C. prema točki E
- D. prema točki A
Vektorskim zbrajanjem odredite smjer i orijentaciju rezultantnog električnog polja u točki B.
Četiri naboja, jednaka po iznosu, fiksirana su u vrhovima kvadrata: \[q_{1}=q_{2}=q_{3}=q_{4}=q\] Točka B jednako je udaljena od sva četiri naboja pa su zato iznosi električnog polja sva četiri naboja u toj točki jednaki.
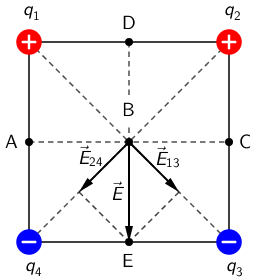
Električno polje naboja \(q_{1}\) u točki B jednako je električnom polju naboja \(q_{3}\) u toj točki. Rezultantno električno polje ta dva naboja na slici je označeno s \(\vec{E}_{13}\): \[\vec{E}_{13}=\vec{E}_{1}+\vec{E}_{3}\] Električno polje naboja \(q_{2}\) u točki B jednako je električnom polju naboja \(q_{4}\) u toj točki. Rezultantno električno polje ta dva naboja na slici je označeno s \(\vec{E}_{24}\): \[\vec{E}_{24}=\vec{E}_{2}+\vec{E}_{4}\] Rezultantno električno polje sva četiri naboja na slici je označeno s \(\vec{E}\) i jednako je \[\vec{E}=\vec{E}_{13}+\vec{E}_{24}\] To polje odredimo pomoću pravila paralelograma za zbrajanje vektora.
10. zadatak
Pločasti kondenzator određenoga kapaciteta priključi se na izvor stalnoga napona. Dok je kondenzator spojen na izvor, poveća se razmak između ploča.
Koja je od navedenih tvrdnja o stanju kondenzatora u opisanim uvjetima točna?
- A. Povećao se kapacitet kondenzatora.
- B. Smanjio se kapacitet kondenzatora.
- C. Smanjio se napon na kondenzatoru.
- D. Povećao se naboj na kondenzatoru.
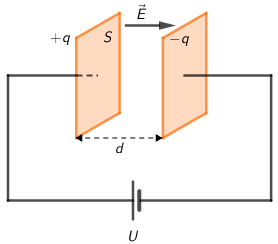
Kapacitet pločastog kondenzatora: \[C=\varepsilon_{0}\,\varepsilon_{r}\,\frac {S}{d}\]
- \(\varepsilon_{0}\) - permitivnost vakuuma
- \(\varepsilon_{\textrm{r}}\) - relativna permitivnost (permitivnost sredstva koje je umetnuto između ploča)
- \(S\) - površina ploče
- \(d\) - udaljenost između ploča
Iznos naboja na pločama: \[q=C\,U\]
Napon između ploča kondenzatora jednak je naponu izvora pa se ne mijenja jer je stalno priključen na izvor.
\[C=\varepsilon_{0}\,\varepsilon_{r}\,\frac {S}{d}\]
Povećanjem razmaka između ploča kapacitet kondenzatora se smanji.
Naboj na pločama
\[q=C\,U\]
također se smanji.
11. zadatak
Na slici je prikazan I, U graf za dvije metalne žice jednakih duljina načinjenih od istoga materijala.
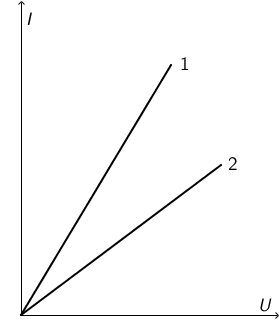
Koji je od navedenih odnosa za električne otpore R1 i R2 i promjere žica d1 i d2 točan?
- A. R1<R2 i d1<d2
- B. R1<R2 i d1>d2
- C. R1>R2 i d1<d2
- D. R1>R2 i d1>d2
Primijenite:
- Ohmov zakon: \[I=\frac{U}{R}\]
- Zakon električnog otpora: \[R=\rho\,\frac{\ell}{S}\]

Iz slike vidimo da je za isti napon struja kroz žicu 1 veća. Na osnovu Ohmovog zakona zaključujemo: \[R_{1} \lt R_{1}\]
Žice su načinjene od istog materijala i imaju jednaku duljinu. Budući da žica 1 ima manji otpor zaključujemo: \[S_{1} \gt S_{2}\Rightarrow d_{1} \gt d_{2}\]
12. zadatak
Vodljiva strujna petlja stalnom brzinom v ulazi u homogeno magnetsko polje indukcije B okomito prema silnicama toga polja kao što je prikazano na slici.
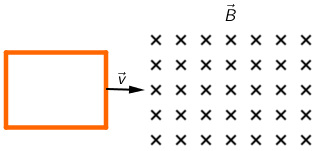
Koji graf ispravno prikazuje ovisnost inducirane struje o vremenu za ovaj slučaj?

- A. Graf A.
- B. Graf B.
- C. Graf C.
- D. Graf D.
Faradayev zakon
Inducirani elektromotorni napon u strujnoj petlji koja se giba okomito na magnetsko polje:
\[u_{\textrm{i}}=-\frac{\Delta \phi}{\Delta t}\]
Magnetsko polje je homogeno pa se promjena magnetskog toka ostvaruje promjenom površine kroz koju prolaze linije sile magnetskog polja:
\[\Delta \phi=\Delta \left(B\,S\right)=B\,\Delta S\]
Predznak minus je zbog Lenzovog pravila:
Inducirani elektromotorni napon u petlji uzrokuje induciranu struju koja je tako orijentirana da stvara magnetsko polje koje se suprotstavlja promjeni
magnetskog toka vanjskog magnetskog polja \(\vec{B}\) koji prolazi kroz petlju.
Lenzovo pravilo možemo iskazati i ovako:
Sila kojom magnetsko polje djeluje na induciranu struju jednaka je po iznosu i suprotno orijentirana od vanjske sile kojom vučemo ili guramo petlju kroz
magnetskog polje.
Pokrenite video.
Od \(t=0\,\textrm{s}\,\textrm{do}\, t=1\,\textrm{s}\)
Petlja se giba izvan magnetskog polja.
\[u_{\textrm{i}}=-\frac{\Delta \phi}{\Delta t}=-B\,\frac{\Delta S}{\Delta t}=0\]
Inducirani napon i inducirana struja jednaki su nuli:
\[u_{\textrm{i}}=0\]
\[i_{\textrm{i}}=0\]
Od \(t=1\,\textrm{s}\,\textrm{do}\, t=2,75\,\textrm{s}\)
Petlja ulazi u magnetsko polje. Magnetski tok povećava se linearno pa je brzina promjene magnetskog toka konstantna, a po predznaku pozitivna:
\[\frac{\Delta \phi}{\Delta t} \gt 0\]
Prema Faradayevom zakonu inducirani napon je konstantan, a po predznaku negativan:
\[u_{\textrm{i}}=-\frac{\Delta \phi}{\Delta t} \lt 0\]
Inducirana struja, prema Ohmovom zakonu:
\[i_{\textrm{i}}=\frac{u_{\textrm{i}}}{R}\]
mijenja se jednako kao i napon, no njezina se vrijednost najčešće razlikuje od vrijednosti induciranog napona.
Plavo obojeni vektori pokazuju da je inducirana struja orijentirana suprotno od kazaljke sata.
Od \(t=2,75\,\textrm{s}\,\textrm{do}\, t=4,25\,\textrm{s}\)
Petlja se giba unutar magnetskog polja. Magnetski tok kroz petlju se ne mijenja:
\[u_{\textrm{i}}=-\frac{\Delta \phi}{\Delta t}=0\]
Inducirani napon i inducirana struja jednaki su nuli:
\[u_{\textrm{i}}=0\]
\[i_{\textrm{i}}=0\]
Od \(t=4,25\,\textrm{s}\,\textrm{do}\, t=6\,\textrm{s}\)
Petlja izlazi iz magnetskog polja. Magnetski tok smanjuje se linearno pa je brzina promjene magnetskog toka konstantna, a po predznaku negativna:
\[\frac{\Delta \phi}{\Delta t} \lt 0\]
Prema Faradayevom zakonu inducirani napon je konstantan, a po predznaku pozitivan:
\[u_{\textrm{i}}=-\frac{\Delta \phi}{\Delta t} \gt 0\]
Inducirana struja mijenja se na sličan način kao i inducirani napon.
Plavo obojeni vektori pokazuju da je inducirana struja orijentirana kao kazaljka sata.
Od \(t=6\,\textrm{s}\,\textrm{do}\, t=7\,\textrm{s}\)
Petlja se giba izvan magnetskog polja.
\[u_{\textrm{i}}=-\frac{\Delta \phi}{\Delta t}=-B\,\frac{\Delta S}{\Delta t}=0\]
Inducirani napon i inducirana struja jednaki su nuli:
\[u_{\textrm{i}}=0\]
\[i_{\textrm{i}}=0\]
Interaktivni aplet Elektromagnetska indukcija - primjer, pomoću kojega je snimljen video, omogućuje vam detaljniji prikaz rješenja ovog zadatka. Kliknite na dugme Ručno i pomoću klizača \(t\) pomičite petlju te promatrajte grafove magnetskog toka i induciranog napona.
Napomena
NCVVO nije ponudio ovakvo rješenje. Graf naveden pod B ima sličan oblik, ali su predznaci struje pogrešno nacrtani jer u Faradayevom zakonu nisu
uzeli u obzir Lenzovo pravilo.
NCVVO nije ponudio točan odgovor za ovaj zadatak. Priznavali su odgovor B. kao točan.
Graf magnetskog toka koji prolazi kroz petlju:
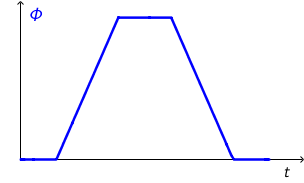
Primjenom Faradayovog zakona \[u_{\textrm{i}}=-\frac{\Delta \phi}{\Delta t}\] zaključujemo da graf induciranog napona izgleda ovako:
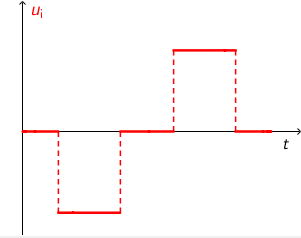
Primjenom Ohmovog zakona \[i_{\textrm{i}}=\frac{u_{\textrm{i}}}{R}\] zaključujemo da će i graf inducirane struje imati jednak oblik.
13. zadatak
Koja je od navedenih tvrdnja točna za matematičko njihalo tijekom titranja?
- A. Brzina i akceleracija tijela jednake su nuli kada je tijelo u ravnotežnome položaju.
- B. Brzina i akceleracija tijela jednake su nuli kada je tijelo u amplitudnome položaju.
- C. Brzina i akceleracija tijela nisu nikad istodobno jednake nuli.
- D. Brzina tijela u amplitudnome je položaju maksimalna, a akceleracija tijela tada je jednaka nuli.
Matematičko njihalo je malena kuglica ovješena na tanku nerastezljivu nit. Ako kuglicu otklonimo iz ravnotežnog položaja za mali kut i ispustimo ju, ona će harmonijski titrati.
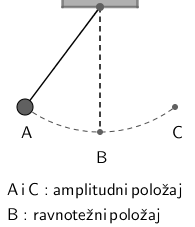
Pokrenite video.
Iz grafa u videu zaključujemo da brzina i akceleracija nikada istodobno ne mogu biti jednake nuli.
14. zadatak
Val amplitude A prostire se brzinom v kroz neko sredstvo. Kada prijeđe u
drugo sredstvo, brzina mu postane 2 v.
Koja je od navedenih tvrdnja točna za valnu duljinu vala u drugome sredstvu?
- A. Prepolovi se.
- B. Ostane ista kao u prvome sredstvu.
- C. Udvostruči se.
- D. Učetverostruči se.
Brzina širenja vala frekvencije \(f\): \[v=f\,\lambda\] Frekvencija titranja izvora vala neovisna je o sredstvu kojim se val širi. Iz navedenog izraza za brzinu zaključujemo da je valna duljinu proporcionalna brzini širenja vala.
Valna duljina vala jednaka je: \[\lambda=\frac{v}{f}\] Ako se brzina širenja vala poveća dva puta, povećat će se i valna duljina dva puta jer je frekvencija titranja izvora vala konstantna.
15. zadatak
Brzina zvuka:
- vz u zraku
- vv u željezu
- vž u željezu
Koji je od navedenih odnosa točan za brzinu širenja u navedenim sredstvima?
- A. vz > vv > vž
- B. vz = vv = vž
- C. vz<vv = vž
- D. vz<vv <vž
Brzina zvuka ovisi o elastičnosti i gustoći sredstva. Elastične sile najveće su u čvrstim tijelima, a najmanje u plinovitim tijelima.
Širenje progresivnog vala kroz neko sredstvo u osnovi je prijenos energije s jedne čestice na drugu, s druge na treću itd. Energija se najbrže prenosi u čvrstim tijelima, a najsporije u plinovima. Točan odgovor je D.
16. zadatak
Koliko iznosi upadni kut zrake svjetlosti koja iz zraka upada na površinu vode ako se reflektirana zraka vrati u izvor?
- A. 0 oC
- B. 45 oC
- C. 60 oC
- D. 90 oC
Zraka svjetlosti koja iz zraka upada u vodu djelomično se lomi, a djelomično odbija. Lomljena zraka nije bitna za ovaj zadatak.
Prema zakonu odbijanja, upadna i odbijena zraka leže u ravnini koja je okomita na površinu vode, a kut upadanja jednak je kutu odbijanja.
Pokrenite video.
U videu vidimo da zraka svjetlosti mora upasti pod kutom \(\alpha=0^{\textrm{o}}\).
17. zadatak
Razmak između zastora i pukotina u Youngovu se pokusu udvostruči.
Što se zbog toga dogodi s razmakom između susjednih svijetlih pruga na zastoru ako se ostatak eksperimentalnoga postava ne mijenja?
- A. Dvostruko se smanji.
- B. Ostane isti.
- C. Dvostruko se poveća.
- D. Četverostruko se poveća.
Udaljenost između svjetlih pruga interferencije u Youngovom pokusu jednaka je: \[s=\frac{\lambda\,a}{d}\]
- \(s\) - udaljenost između susjednih svjetlih ili tamnih pruga.
- \(\lambda\) - valna duljina upadne svjetlosti.
- \(d\) - udaljenost između pukotina kroz koje prolazi svjetlost.
- \(a\) - udaljenost između zastora i pukotina kroz koje prolazi svjetlost.
Iz izraza za udaljenost između svjetlih pruga interferencije: \[s=\frac{\lambda\,a}{d}\] zaključujemo da će se udaljenost između susjednih svjetlih pruga povećati dva puta.
18. zadatak
Koja je od navedenih tvrdnja o magnetskome polju radiovalova točna?
- A. Paralelno je s električnim poljem vala i sa smjerom širenja vala.
- B. Paralelno je s električnim poljem vala i okomito na smjer širenja vala.
- C. Okomito je na električno polje vala i na smjer širenja vala.
- D. Okomito je na električno polje vala i paralelno sa smjerom širenja vala.
Radiovalovi su elektromagnetski valovi kojima je valna duljina veća od jednog milimetra pa do stotinjak tisuća kilometara. U elektromagnetskom valu električno i magnetsko polje titraju u međusobno okomitim ravninama i obje su ravnije okomite na smjer širenja elektromagnetskog vala. To znači da su elektromagnetski valovi transverzalni.
Točan odgovor je C.
19. zadatak
Elektron se giba brzinom 1 km/s.
Kolika mu je valna duljina?
- A. 0,397 nm
- B. 1,43 nm
- C. 0,727 μm
- D. 2,62 μm
De Broglieva valna duljina čestice mase \(m\) koja se giba brzinom \(v\): \[\lambda=\frac{h}{m\,v}\]
\[\lambda=\frac{h}{m\,v}=7,27\cdot10^{-7}\,\textrm{m}=0,727\,\mu \textrm{m}\]
20. zadatak
U spektru nekoga elementa opažaju se ljubičasta, plava, zelena i crvena linija. One nastaju prijelazima elektrona koji su na priloženoj slici prikazani strelicama.
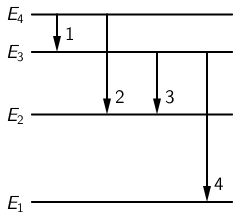
Kojim je brojem označena strelica koja odgovara fotonu ljubičaste svjetlosti?
- A. brojem 1
- B. brojem 2
- C. brojem 3
- D. brojem 4
Atomi ne mogu poprimiti bilo koju energiju, nego samo neke točno određene vrijednosti energije. Te energije zovemo energijske razine.
O vrsti atoma ovise vrijednosti tih dopuštenih energija. Stanje u kojemu se nalazi atom kada mu je energija najmanja zove se osnovno stanje.
Sva druga stanja su pobuđena stanja.
Skup svih dopuštenih energijskih stanja nekog atoma zovemo energijski spektar. Energijski spektar atoma je kvantiziran. To znači da atom može
poprimiti samo točno određene vrijednosti energije.
Ako se atom nađe u nekom pobuđenom stanju, prelazit će spontano u niža energijska stanja sve dok ne dođe do osnovnog stanja. Pritom atom emitira
fotone elektromagnetskog zračenja kojima je energija jednaka razlici energija početnog i konačnog stanja:
\[E_{\textrm{f}}=E_{\textrm{poč}}-E_{\textrm{kon}}\]
Ovaj proces nazivamo emisija zračenja.
Energija fotona kojeg emitira atom pri prijelazu iz višeg u niže energijsko stanje
\[E_{\textrm{f}}=E_{\textrm{poč}}-E_{\textrm{kon}}\qquad(1)\]
može se prikazati kao:
\[E_{\textrm{f}}=h\,f\]
ili kao
\[E_{\textrm{f}}=\frac{h\,c}{\lambda}\]
Valna duljina emitirane svjetlosti obrnuto je proporcionalna energiji fotona:
\[\lambda=\frac{h\,c}{E_{\textrm{f}}}\]
Prema izrazu (1) valnu duljinu emitirane svjetlosti možemo prikazati kao:
\[\lambda=\frac{h\,c}{E_{\textrm{poč}}-E_{\textrm{kon}}}\]
Od navedenih fotona, foton ljubičaste svjetlosti ima najmanju valnu duljinu, a to znači da je razlika između energije početnog i konačnog stanja
najveća.
Na slici vidimo da se radi o prijelazu koji odgovara strelici 4.
21. zadatak
Energija vezanja po nukleonu za tricij \(_1^3\textrm{H}\) iznosi približno 2,8 MeV.
Kolika je najmanja energija potrebna za rastavljanje jezgre na nukleone?
- A. 2,8 MeV
- B. 5,6 MeV
- C. 8,4 MeV
- D. 11,2 MeV
Masa jezgre \(m_{\textrm{j}}\) manja je od zbroja mase slobodnih protona i neutrona koji čine jezgru
\(\left(Z\cdot m_{\textrm{p}}+\left (A-Z \right )\cdot m_{\textrm{n}}\right)\)
Tu razliku u masama zovemo defekt mase. Znak za defekt mase je \(\Delta m\).
Odredimo defekt mase za jezgru \({_\textrm{Z}^\textrm{A}}\textrm{X}\):
\[\Delta m=Z\cdot m_{\textrm{p}}+\left (A-Z \right )\cdot m_{\textrm{n}}-m_{\textrm{j}}\]
Prema posebnoj teoriji relativnosti, ta je masa proporcionalna energiji koju zovemo energija vezanja jezgre:
\[E_{\textrm{v}}= \Delta m\cdot c^{2}\]
Kada bismo sastavljali jezgru od protona i elektrona, ta bi se energija oslobodila. Ako bismo jezgru razbijali, morali bismo obaviti rad koji je
jednak energiji vezanja jezgre.
Energiju vezanja jezgre po nukleonu dobijemo dijeljenjem energije vezanja s brojem nukleona u jezgri: \[E'_{\textrm{v}}=\frac{E_{\textrm{v}}}{A}\]
Iz energije vezanja jezgre po nukleonu odredimo energiju vezanja jezgre: \[E_{\textrm{v}}=E'_{\textrm{v}}\cdot A\] Jezgra tricija ima tri nukleona: \[A=3\] \[E_{\textrm{v}}=2,8\cdot 3=8,4\,\textrm{MeV}\]
22. zadatak
Bizmut \(^{210}\textrm{Bi}\) radioaktivni je izotop koji se raspada na sljedeći način: \[^{210}\textrm{Bi}\xrightarrow[\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, ]{\large{\beta^{\mathbf{-}}}}\textrm{X}\xrightarrow[\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, ]{\large{\alpha}}\textrm{Y}\] Koliki je maseni broj A i broj protona Z elementa Y nastaloga pri ovome raspadu?
- A. A = 214 i Z = 80
- B. A = 206 i Z = 82
- C. A = 206 i Z = 80
- D. A = 210 i Z = 82
Simbolički zapis jezgre atoma: \[_{Z}^{A}\,\textrm{X}\]
- \(Z\) - protonski broj koji je jednak broju protona u jezgri
- \(A\) - nukleonski broj koji je jednak broju nukleona u jezgri. Nukleoni su protoni i neutroni.
- \(\textrm{X}\) - simbolički znak jezgre atoma koji je jednak kemijskom simbolu atoma kojemu jezgra pripada.
U periodnom sustavu pročitamo protonski broj za bizmut: Z = 83.
Beta-minus raspad:
\[_{\;83\,}^{210\,}\textrm{Bi}\rightarrow _{Z}^{A}\textrm{X}+_{-1}^{\;\;0}\textrm{e}\]
Pri radioaktivnom raspadu očuvani su protonski i nukleonski broj.
\[83=Z-1\Rightarrow Z=84\]
\[210=A+0\Rightarrow A=210\]
U periodnom sustavu pročitamo da je jezgra X jezgra polonija.
Polonij se raspada uz emisiju alfa-čestica.
\[_{\;84\,}^{210\,}\textrm{Po}\rightarrow _{Z}^{A}\textrm{Y}+_{2}^{4}\textrm{He}\]
Ponovno primijenimo očuvanje protonskog i nukleonskog broja:
\[84=Z+2\Rightarrow Z=82\]
\[210=A+4\Rightarrow A=206\]
Točan odgovor je B.
Napomena
U zadatku se ne traži koja je jezgra Y, ali u periodnom sustavu pročitamo da je jezgra Y jezgra olova.
23. zadatak
Kapetan u svemirskome brodu zatitra tijelo ovješeno o oprugu frekvencijom
f0 mjereno u sustavu broda.
Pretpostavite da se svemirski brod giba u odnosu na Zemlju nekom relativističkom brzinom.
Koju bi od navedenih frekvencija titranja f istoga tijela mogao mjeriti motritelj sa Zemlje?
- A. 2 f0
- B. 1,5 f0
- C. f0
- D. 0,8 f0
Kapetan svemirskog broda mjeri vlastiti period titranja tijela \(T_{0}\), a promatrač sa Zemlje za period titranja izmjeri \(T\): \[T=\frac{T_{0}}{\sqrt{1-v^2/c^2}}\]
Vlastita frekvencija (kapetan u svemirskom brodu): \[f_{0}=\frac{1}{T_{0}}\] Frekvencija koju mjeri promatrač sa Zemlje: \[f=\frac{1}{T}\] Podijelimo drugi izraz s prvim: \[\frac{f}{f_0}=\frac{1}{T}\cdot \frac{T_{0}}{1}\] \[\frac{f}{f_0}=\frac{T_{0}}{T}\] Iz izraza za dilataciju vremena: \[T=\frac{T_{0}}{\sqrt{1-v^2/c^2}}\] dobijemo: \[\frac{T_{0}}{T}=\sqrt{1-v^2/c^2} \lt 1\] Prema tome: \[\frac{f}{f_0} \lt 1\] ili: \[f \lt f_{0}\] Točan odgovor je D.
24. zadatak
Sunce je zvijezda koja je vidljiva zbog svjetlosti koju odašilje u svemir.
Koliki se postotak svemira sastoji od vidljive tvari?
- A. < 10 %
- B. 10 % - 50 %
- C. 51 % - 90 %
- D. > 90 %
Svemir
- Sve zvijezde i galaksije sastoje se od vidljive tvari. U cijelom svemiru samo oko 5% tvari je vidljivo.
- Tamna tvar ne djeluje elektromagnetskom silom. Ona ne apsorbira, ne odbija i ne emitira svjetlost. Njezino postojanje objašnjavamo samo gravitacijskim djelovanjem na vidljivu tvar. Pretpostavlja se da u cijelom svemiru ima oko 27 % tamne tvari.
- Približno 68% svemira sastoji se od tamne energije, koja je jednoliko raspoređena po cijelom svemiru. Tamna energija djeluje na svemir kao cjelinu. Ubrzano širenje svemira objašnjava se odbojnom silom kojom djeluje tamna energija.
Točan odgovor je A.
25. zadatak
U plastičnoj boci volumena 0,5 litara nalazi se zrak pri atmosferskome tlaku. Zrak se smatra idealnim plinom.
Kada se boca stisne, tlak zraka u boci poveća se za četvrtinu njegove početne vrijednosti.
Koliki je konačni volumen zraka u boci ako mu je temperatura stalna?
Odgovor: \(\ell\)
Izotermna promjena stanja plina (temperatura plina je konstantna): \[P_{1}\,V_{1}=P_{2}\,V_{2}\]
- \(P_{1}\,\textrm{i}\,V_{1}\) - početni tlak i volumen plina
- \(P_{2}\,\textrm{i}\,V_{2}\) - konačni tlak i volumen plina
\[P_{1}=P_{\textrm{a}}\] \[V_{1}=0,5\,\ell\] \[P_{2}=P_{\textrm{a}}+\frac{1}{4}\,P_{\textrm{a}}=\frac{5}{4}\,P_{\textrm{a}}\] \[V_{2}=\frac{P_{1}\,V_{1}}{P_{2}}\] \[V_{2}=0,4\,\ell\]
26. zadatak
Svjetlost upada iz zraka na obojeno staklo indeksa loma n = 1,5.
Koliko iznosi upadni kut svjetlosti ako je kut loma jednak 30o?
Odgovor: \(^{\textrm{o}}\)
Zakon loma svjetlosti
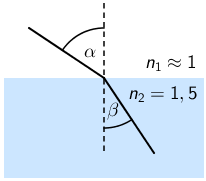
\[\textrm{sin}\,\alpha=\frac{n_{2}}{n_{1}}\,\textrm{sin}\,\beta\] \[\alpha=48,59^{\textrm{o}}\]
27. zadatak
U čaši se nalazi voda na koju se pažljivo nalije ulje tako da se ne miješa s vodom. U čašu se potom stavi tijelo nepoznate gustoće
tako da pluta između tekućina i potpuno je u njih uronjeno.
Kolika je gustoća tijela ako se 45 % njegova volumena nalazi u vodi?
ρvode = 1000 kg/m3,
ρulja = 900 kg/m3
Odgovor: kg/m3
Na tijelo uronjeno u fluid djeluju uzgon i sila teža. Sila teža djeluje vertikalno prema dolje, dok je uzgon suprotno orijentiran od sile teže: \[F_{\textrm{u}}=\rho_{\textrm{f}}^{\,}\, g\, V_{\textrm{udt}}\]
- \(\rho_{\textrm{f}}^{\,}\) - gustoća fluida
- \(V_{\textrm{udt}}\) - volumen uronjenog dijela tijela
Sila teža, \(F_{\textrm{g}}=m\,g\) može se prikazati pomoću gustoće tijela \(\rho\) i volumena tijela \(V\): \[F_{\textrm{g}}=\rho\,V\,g\]
Na tijelo djeluju sila teža \(F_{g}\), uzgon vode \(F_{\textrm{u,vode}}\) i uzgon ulja \(F_{\textrm{u,ulja}}\).

\[F_{\textrm{g}}=\rho\,V\,g\] Uzgon vode djeluje samo na dio volumena tijela koji je uronjen u vodu: \[F_\textrm{u,vode}=ρ_\textrm{vode}\,g\,V_\textrm{u vodi}\] Uzgon ulja djeluje samo na dio volumena tijela koji je uronjen u ulje: \[F_\textrm{u,ulja}=ρ_\textrm{ulja}\,g\,V_\textrm{u ulju}\] Tijelo pluta, a to znači da je rezultanta sve tri sile jednaka nuli: \[\vec{F}_\textrm{g}=\vec{F}_\textrm{u,vode}+\vec{F}_\textrm{u,ulja}\] Iznos sile teže mora biti jednak zbroju iznosa uzgona vode i ulja: \[\rho\,V\,g=ρ_\textrm{vode}\,g\,V_\textrm{u vodi}+ρ_\textrm{ulja}\,g\,V_\textrm{u ulju}\] \[V_\textrm{u vodi}=0,45\,V\] \[V_\textrm{u ulju}=0,55\,V\] \[\rho\,V\,g=1000\cdot g\cdot 0,45\,V+900\cdot g\cdot 0,55\,V\] \[\rho=1000\cdot 0,45+900\cdot 0,55\] \[\rho=945\,\textrm{kg/m}^{3}\]
28. zadatak
Koliko se nekomu idealnom plinu mora izotermno dovesti topline kako bi mu se pri normiranome atmosferskom tlaku volumen povećao s 4 m3 na 6 m3?
Odgovor: J
Unutarnja energija nekog tijela ili sustava jednaka je zbroju srednje kinetičke i srednje potencijalne energije svih čestica (molekula, atoma, ...) tijela ili sustava: \[U=N\left(\overline{E}_{\textrm{k}}+\overline{E}_{\textrm{p}}\right)+\cdot \cdot \cdot\] Unutarnja energija obuhvaća kinetičku i potencijalnu energiju molekula, atoma unutar molekule, elektrona u atomu itd. Zbog toga ju je moguće točno odrediti samo za idealni plin. U modelu idealnog plina zanemarujemo potencijalnu energiju molekula. Zato je unutarnja energija idealnog plina jednaka srednjoj kinetičkoj energiji svih molekula. Označimo ukupan broj molekula s \(N\): \[U=N\,\overline{E}_{\textrm{k}}=\frac{i}{2}\,N\,k\,T\]
- \(i=3\) za jednoatomni idealni plin
- \(i=5\) za dvoatomni idealni plin
Promjenu unutarnje energije sustava moguće je odrediti pomoću prvog zakona termodinamike: \[\Delta U= Q - W\]
- \(\Delta U=U_{2}-U_{1}\) - promjena unutarnje energije sustava (razlika unutarnjih energija u konačnom i početnom stanju)
- \(Q\) - toplina koju sustav prima od okoline \(\left(Q \gt 0\right)\) ili predaje okolini \(\left(Q \lt 0\right)\)
- \(W\) - rad kojeg sustav obavlja nad okolinom \(\left(W \gt 0\right)\) ili okolina obavlja nad sustavom \(\left(W \lt 0\right)\)
Promjena unutarnje energije sustava jednak je razlici energije koju sustav prima zagrijavanjem i rada kojeg sustav obavlja nad okolinom.
Prvi zakon termodinamike je matematički zapis općeg zakona o očuvanju energije, pri čemu su uključeni unutarnja energija,
toplina i mehanički rad.
Prvi zakon termodinamike zapisujemo i u obliku:
\[Q = W + \Delta U\]
Toplina dovedena sustavu pretvara se u mehanički rad i unutarnju energiju.
U termodinamičkom sustavu energija ne može nastati ni nestati sama po sebi, jedino može prelaziti iz jednog oblika u drugi.
Zakon očuvanja energije moguće je formulirati i ovako:
Ukupna energija zatvorenog sustava je konstantna.
Primijenimmo prvi zakon termodinamike \[Q = W + \Delta U\] na izotermni proces idealnog plina: \[T=\textrm{konst.}\Rightarrow \Delta T=0\] U tom se procesu unutarnja energija ne mijenja: \[\Delta U=0\] Toplina koju plin prima pretvara se u rad kojega plin obavlja nad okolinom: \[Q = W\]
Napomena
U zadatku je trebalo napisati da se plin nalazi u posudi koja je zatvorena pomičnim klipom zanemarive mase.
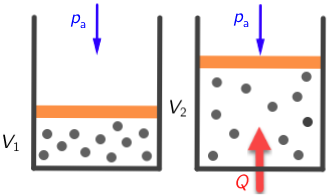
Plin obavlja rad nad okolnim zrakom pri normiranom tlaku: \[W=p_{\textrm{a}}^{\,}\,\Delta V\] Toplina koju je plin primio jednaka je radu kojega je plin obavio: \[Q=W=p_{\textrm{a}}^{\,}\,\Delta V\] \[Q=202650\,\textrm{J}=2,03\cdot 10^{5}\,\textrm{J}\]
Koliko se nekomu idealnom plinu mora izotermno dovesti topline kako bi mu se pri normiranome atmosferskom tlaku volumen povećao s 4 m3 na 6 m3?
Neprecizna formulacije zadatka bila je razlog zbog kojega su učenici ulagali prigovor na taj zadatak. NCVVO je odgovorio na pitanja koja mu je postavio portal srednja.hr
Od stručne skupine za fiziku Nacionalnog centra na kraju smo dobili i osvrt na navode s društvenih mreža, koje smo priložili gore u screenshotu.
- Uistinu, za zatvoren sustav idealnog plina, ukoliko je neka promjena izotermna i izobarna, tad nema promjene volumena, pa je izvršen rad nula. No, ukoliko je sustav otvoren, navedeno ne mora biti istinito, što je u komentaru primijećeno. No, nije nužno istina da tad broj molekula u sustavu mora biti promjenjiv. Slažemo se da on to može biti, no kao i u drugim zadacima u fizici, implicitno se podrazumijeva stalnost broja molekula, stoji u dopisu stručne skupine.
- Takve su implicitne pretpostavke, dodaju, ‘ugrađene’ u gotovo sve zadatke u fizici. Tako primjerice kod hitaca se smatra da je jakost gravitacijskog polja u blizini Zemlje stalno, kod klizanja da je koeficijent trenja neovisan o vremenu, iako ni jedna, kažu, od te dvije tvrdnje nije sasvim istinita.
- Te se pretpostavke ne navode u svakom zadatku i očekuje se da su jasne same po sebi. Učenici koji u školi uče koncept izotermne promjene idealnog plina nauče da to podrazumijeva stalnost unutarnje energije tog plina, što se i ovdje podrazumijevalo. Uz to razumijevanje zadatak ima jedinstveno rješenje, jer za sve sustave vrijedi prvi zakon termodinamike, zaključuju u odgovoru iz NCVVO-a.
Komentar
-
SRS nije dobro razumjela zadatak. Ovdje se radi o izotermnoj promjeni stanja plina pa se tlak plina pri širenju smanjuje:
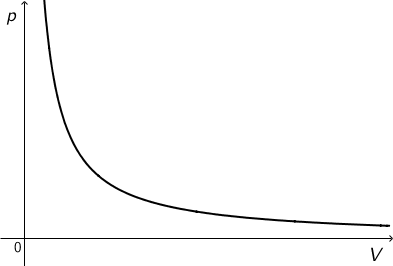
U zadatku je trebalo napisati da se idealni plin nalazi u posudi zatvorenoj pomičnim klipom zanemarive mase.
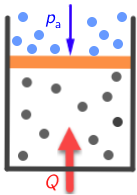
Plin nalazi u posudi zatvorenoj pomičnim klipom pa ne dolazi do izmjene čestica između plina u posudi i okoline. SRS je napisala "implicitno se podrazumijeva stalnost broja molekula".
Ovdje se ne radi o tome da se plin u posudi nalazi pod normiranim atmosferskim tlakom, nego o tome da plin pri izotermnom procesu, u kojemu se njegova unutarnja energija ne mijenja, obavlja rad nad okolnim zrakom koji se nalazi pod normiranim atmosferskim tlakom. Toplina koju plin prima pretvara se u rad potreban da se njegov volumen poveća od 4 m3 do 6 m3. Na osnovu prvog zakona termodinamike slijedi da je \[Q=W,\] odnosno \[Q=p_{\textrm{a}}\,\Delta V\]
29. zadatak
Pločasti kondenzator kapaciteta 44 pF spojen je na izvor napona U. Između ploča
kondenzatora je zrak. Kada se kondenzator, dok je i dalje priključen na izvor napona, stavi u ulje relativne permitivnosti 2,59, količina
naboja na pločama kondenzatora promijeni se za 35 nc.
Koliki je iznos napona U?
Odgovor: V
Kapacitet pločastog kondenzatora; \[C=\varepsilon_{0}\,\varepsilon_{r}\,\frac {S}{d}\] Naboj na pločama kondenzatora koji je priključen na napon U: \[q=C\,U\]
Kapacitet kondenzatora ako se između njegovih ploča nalazi zrak: \[C_{0}=\varepsilon_{0}\,\frac {S}{d}\] Ako kondenzator stavimo u ulje, njegov je kapacitet: \[C=\varepsilon_{0}\,\varepsilon_{r}\,\frac {S}{d}\] Podijelimo ova dva izraza: \[\frac{C}{C_{0}}=\varepsilon_{r}\] \[C=\varepsilon_{r}\,C_{0}\] Ako kondenzator stavimo u ulje, naboj na njegovim pločama poveća se za \(\Delta q=35\,\textrm{nC}\): \[q_{0}=C_{0}\,U;\textrm{naboj na pločama u zraku}\] \[q=C\,U;\textrm{naboj na pločama u ulju}\] \[\Delta q=q-q_{0}\] \[\Delta q=C\,U-C_{0}\,U\] \[\Delta q=U\left(C-C_{0}\right)\] \[\Delta q=U\left(\varepsilon_{r}\,C_{0}-C_{0}\right)\] \[\Delta q=U\,C_{0}\left(\varepsilon_{r}-1\right)\] Napon između ploča kondenzatora je: \[U=\frac{\Delta q}{C_{0}\left(\varepsilon_{r}-1\right)}\] \[U=500,29\,\textrm{V}\approx{500}\,\textrm{V}\]
30. zadatak
Granična valna duljina za nastanak fotoelektričnoga efekta kod kalcija iznosi
λ0 = 384 nm.
Koliko iznosi napon pri kojemu će se zaustavljati elektroni emitirani iz kalcija kada se kalcij obasja svjetlošću valne duljine
λ = 250 nm
Odgovor: V
Granična valna duljina \(\lambda_{0}\) je najveća valna duljina pri kojoj se fotoelektrični učinak još opaža. Izlazni rad elektrona iz metala moguće je odrediti pomoću granične valne duljine: \[W_{0}=\frac{h\,c}{\lambda_{0}}\] Na osnovu Einsteinove jednadžbe energija fotona svjetlosti koja pada metal pretvara se u svladavanje izlaznog rada i kinetičku energiju elektrona izbačenih iz metala: \[E_{\textrm{f}}=W_{0}+E_{\textrm{k}}\]
Energija fotona svjetlosti koja pada na metal: \[E_{\textrm{f}}=\frac{h\,c}{\lambda}\] Najveću kinetičku energiju elektrona izbačenih iz metala odredimo na osnovu Einsteinove jednadžbe: \[E_{\textrm{k}}=E_{\textrm{f}}-W_{0}\] \[E_{\textrm{k}}=\frac{h\,c}{\lambda}-\frac{h\,c}{\lambda_{0}}\] \[E_{\textrm{k}}=h\,c\left(\frac{1}{\lambda}-\frac{1}{\lambda_{0}}\right)\] Fotoelektrone puštamo kroz električno polje napona \(U\). Za zaustavljanje elektrona električno polje obavi rad \(W=e\,U\) koji mora biti jednak kinetičkoj energiji najbržih elektrona: \[W=E_{\textrm{k}}\] \[e\,U=h\,c\left(\frac{1}{\lambda}-\frac{1}{\lambda_{0}}\right)\] Iz ovog izraza odredimo zaustavni napon: \[U=\frac{h\,c}{e}\,\left(\frac{1}{\lambda}-\frac{1}{\lambda_{0}}\right)\] \[U=1,73\,\textrm{V}\]
31. zadatak
Motor dizalice ima snagu 1050 W. Teret mase 300 kg dizalica podigne na visinu
8 m8 za jednu minutu.
Kolika je korisnost te dizalice?
Odgovor: %
Korisnost nekog stroja jednaka je omjeru korisnog rada (energije; snage) i uložene energije (rada; snage): \[\eta=\frac{P_{\textrm{k}}}{P_{\textrm{u}}}\]
\[P_{\textrm{u}}=1050\,\textrm{W}\] \[P_{\textrm{k}}=\frac{m\,g\,h}{t}\] \[P_{\textrm{k}}=\frac{300\cdot 10\cdot 8}{60}\] \[P_{\textrm{k}}=400\,\textrm{W}\] \[\eta=\frac{P_{\textrm{k}}}{P_{\textrm{u}}}\] \[\eta=\frac{400}{1050}=0,381\] Korisnost dizalice je \(\eta=0,381\,\textrm{ili 38,1 %}\)
32. zadatak
Kuglicu mase \(m\) pustimo da slobodno pada s visine 25 m. Istodobno ispod nje s tla izbacimo drugu kuglicu iste mase \(m\)
vertikalno prema gore. Kuglice se sudare i nastave se gibati zajedno brzinom 3 m/s prema dolje. Netom prije sudara brzina
donje kuglice iznosi 5 m/s prema gore. Otpor zraka je zanemariv.
Na kojoj su se visini iznad tla kuglice sudarile?
Odgovor: m
Put kojega tijelo prijeđe pri slobodnom padu \[s=\frac{g}{2}\,t^{2}\] Visina na kojoj se u nekom trenutku tijelo nalazi pri vertikalnom hicu: \[h=v_{0}^{\,}\,t-\frac{g}{2}\,t^{2}\]
Kuglica 1 ispuštena je s visine \(H\), a kuglica 2 bačena je vertikalno uvis početrnom brzinom \(v_{0}\). Obje su se kuglice počele gibati istodobno.
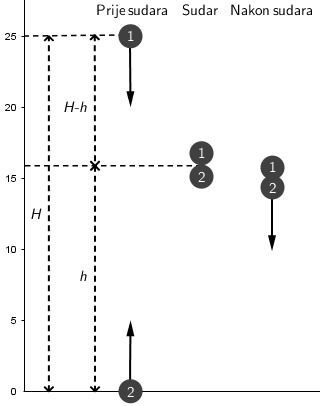
- \(H=25\,\textrm{m}\)
- \(h\) - visina na kojoj se kuglice sudare
- \(H-h\) - put koji je prešla kuglica 1 do sudara s kuglicom 2
\[H-h=\frac{g}{2}\,t^{2}\qquad(1)\] Visina na kojoj se kuglice sudare jednaka je visini na kojoj se nalazi kuglica 2, koja je bačena vertikalno uvis početnom brzinom \(v_{0}\). \[h=v_{0}^{\,}\,t-\frac{g}{2}\,t^{2}\qquad(2)\] Uvrstimo izraz (2) u izraz(1): \[H-v_{0}^{\,}\,t+\frac{g}{2}\,t^{2}=\frac{g}{2}\,t^{2}\] \[H=v_{0}^{\,}\,t\qquad(3)\] Brzina kuglice 2 neposredno prije sudara jednaka je brzini kod vertikalnog hica: \[v=v_{0}^{\,}-g\,t\] Ta je brzina zadana u zadatku: v = 5 m/s. \[v_{0}^{\,}=v+g\,t\qquad(4)\] Izraz (4) uvrstimo u izraz (3): \[H=v\,t+g\,t^{2}\] \[g\,t^{2}+v\,t-H=0\] Dobili smo kvadratnu jednadžbu iz koje ćemo izračunati vrijeme \(t\) nakon kojega su se kuglice sudarile: \[10\,t^{2}+5\,t-25=0\] \[2\,t^{2}+t-5=0\] \[t=\frac{-1\pm\sqrt{1+40}}{4}\] Kuglice se sudare nakon \[t=1,35078\,\textrm{s}\] od početka gibanja. Visinu na kojoj su se kuglice sudarile odredimo iz izraza (1): \[h=H-\frac{g}{2}\,t^{2}\] \[h=15,88\,\textrm{m}\]

Koristili su zakon očuvanja količine gibanja.
- \(v_{1}^{\,}\) - brzina kuglice 1 neposredno prije sudara
- \(v_{2}^{\,}=5\,\textrm{m/s}\) - brzina kuglice 2 neposredno prije sudara
- \(v_{12}^{\,}=3\,\textrm{m/s}\) - brzina kuglica 1 i 2 nakon neelastičnog sudara
\[-m\,v_{1}^{\,}+m\,v_{2}^{\,}=-2m\,v_{12}^{\,}\] \[v_{1}^{\,}=v_{2}^{\,}+2\,v_{12}^{\,}\] \[v_{1}^{\,}=11\,\textrm{m/s}\] Kada nam je poznata brzina kuglice 1 na visini gdje su se kuglice sudarile, moguće je odrediti i tu visinu: \[v_{1}^{2}=2\,g\left(H-h\right)\] \[h=H-\frac{v_{1}^{2}}{2g}\] \[h=18,95\,\textrm{m}\]
Provjerimo korektnost rješenja
Odredimo vrijeme nakon kojega je došlo do sudara.
Kuglica 1 došla je do točke sudara nakon vremena:
\[t_{1}^{\,}=\frac{v_{1}^{\,}}{g}\]
\[t_{1}^{\,}=1,1\,\textrm{s}\]
Odredimo početnu brzinu kojom je kuglica 2 bačena vertikalno uvis:
\[v_{2}^{2}=v_{0}^{2}-2g\,h\]
\[v_{0}^{2}=v_{2}^{2}+2g\,h\]
\[v_{0}^{2}=5^{2}+20\cdot 18,95\]
\[v_{0}^{\,}=20,1\,\textrm{m/s}\]
Odredimo vrijeme nakon kojega je kuglica 2 došla do točke sudara:
\[h=v_{0}^{\,}t_{2}-\frac{g}{2}\,t_{2}^{2}\]
Uvrstimo podatke i riješimo kvadratnu jednadžbu:
\[5\,t_{2}^{2}-20,1\,t_{2}+18,95=0\]
\[t_{2}=\frac{20,1\pm\sqrt{20,1^{2}-4\cdot 5\cdot 18,95}}{10}\]
\[t_{2}=\frac{20,1\pm 5}{10}\]
Dobijemo dva rješenja:
\[t_{2}=1,51\,\textrm{s}\,\textrm{i}\,t_{3}=2,51\,\textrm{s}\]
Kuglice 1 i 2 pokrenute su u gibanje istodobno. Prema NCVVO, na visini 18,95 m kuglica 1 bit će nakon
1,1 s, a kuglica 2 nakon 1,51 s. Jasno je da se na visini koju je NCVVO naveo kao točno
rješenje, do sudara ne može doći.
Gdje je NCVVO pogriješio?
Kuglice su se sudarile nakon \[t=1,35\,\textrm{s}\] Brzina kuglice 1 u tom je trenutku: \[v_{1}^{\,}=g\,t=13,5\,\textrm{m/s}\] a brzina kuglice 2: \[v_{2}^{\,}=5\,\textrm{m/s}\] Primijenimo zakon očuvanja količine gibanja: \[-m\,v_{1}^{\,}+m\,v_{2}^{\,}=-2m\,v_{12}^{\,}\] Brzina kuglica nakon neelastičnog sudara iznosi: \[v_{12}^{\,}=\frac{v_{1}^{\,}-v_{2}^{\,}}{2}\] \[v_{12}^{\,}=4,25\,\textrm{m/s}\] U zadatku su napisali da je ta brzina 3 m/s i to je dovelo do pogrešno određene visine 18,95 m.
Na ocjenjivanju su pravedno postupili pa su kao točan odgovor priznali oba rješenja. Učenik je vjerovao podatku napisanom u zadatku i dobio rezultat
18,95 m.
Priznali su i točan odgovor, ali nisu priznali svoju pogrešku.
NCVVO je ovako napisao u ključu za odgovore:

Naravno da NCVVO neće napisati: Oprostite, pogriješili smo, ali priznat ćemo oba odgovora. Umjesto toga točno rješenje proglašavaju alternativnim, a netočno valjda točnim, uz bespotrebnu napomenu o tome što znači pojam istodobno.
33. zadatak
Promjenjivomu otporniku dovoljno velike snage može se mijenjati otpor od 0 Ω do 1000 Ω.
Žarulja predviđena za istosmjerni napon 12 V ima snagu 2 W dok svijetli. Potrebno je
spojiti devet takvih žarulja i promjenjivi otpornik serijski na izvor istosmjernoga napona od 220 V tako da svaka
žarulja svijetli jednakim sjajem kao da je zasebno priključena na izvor napona od 12 V.
Koliki mora biti otpor promjenjivoga otpornika?
Odgovor: \(\Omega\)
Snaga električne struje: \[P=U\,I\] Ohmov zakon: \[I=\frac{U}{R}\] Ukupni otpor serijski spojenih otpora jednak je njihovom zbroju: \[R_{\textrm{uk}}=R_{1}+R_{2}+R_{3}+\cdot \cdot \cdot\]
Struja koja prolazi kroz jednu žarulju: \[I_{1}=\frac{P}{U_{1}}=\frac{1}{6}\,\textrm{A}\] Otpor jedne žarulje: \[R_{1}=\frac{U_{1}}{I_{1}}=72\,\Omega\] Otpor devet žarulja i promjenjivog otpornika u serijskom spoju: \[R=9\cdot 72+R_{\textrm{p}}\] Žarulje je potrebno spojiti na izvor napona: \[U=220\,\textrm{V}\] Svih devet žarulja mora svjetliti jednakim sjajem kao i jedna žarulja. To znači da kroz serijski spoj devet žarulja i promjenjivi otpornik treba prolaziti jednaka struja kao kroz jednu žarulju: \[I=\frac{U}{R}\] \[I=I_{1}=\frac{1}{6}\,\textrm{A}\] Iz ove dvije jednadžbe slijedi: \[\frac{U}{R}=I_{1}\] \[\frac{220}{9\cdot 72+R_{\textrm{p}}}=\frac{1}{6}\] \[R_{\textrm{p}}=672\,\Omega\]
34. zadatak
Tijelo mase 100 grama titra harmonijski amplitudom 10 cm
i periodom 12 s. Početni fazni kut iznosi 0 rad.
Koliki je iznos sile na tijelo u trenutku kad je proteklo 2 s od početka titranja?
Odgovor: mN
\[F=k\,x\] \[x=A\,\textrm{sin}\left(\omega\,t\right)\]
\[\omega=\frac{2\,\pi}{T}=\frac{\pi}{6}\] \[k=m\,\omega^{2}\] \[F=m\,\omega^{2}A\,\textrm{sin}\left(\omega\,t\right)\] \[F=0,1\cdot \left(\frac{\pi}{6}\right)^{2}\cdot 0,1\cdot \textrm{sin}\left(\frac{\pi}{6}\cdot 2\right)\] \[F=2,37\cdot 10^{-3}\,\textrm{N}=2,37\,\textrm{mN}\]
35. zadatak
Na slici su prikazani potkovasti magnet i ravni vodič.
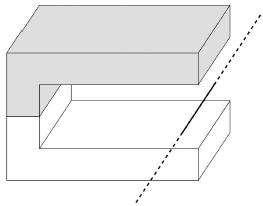
Učenici su na satu Fizike dobili zadatak da istraže silu kojom homogeno magnetsko polje djeluje na vodič kojim prolazi struja i nalazi se u tome magnetskom polju.
35.1. U polje za unos upišite redni broj sile koju učenici trebaju istražiti uz pomoć prikazanoga pribora.
- Ampereova sila
- Lorentzova sila
- Coulombova sila
- gravitacijska sila
Redni broj sile:
35.2. Učenici su dobili zadatak da ispravno označe polove magneta prema smjeru struje u vodiču i smjeru sile koja je djelovala na vodič.
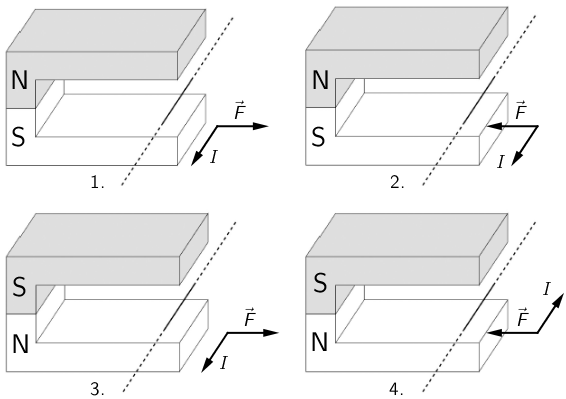
U polje za unos upišite redni broj crteža na kojemu su ispravno označeni polovi magneta.
Redni broj crteža:
35.3. Magnetska indukcija u prostoru gdje se nalazi vodič iznosi 0,1 T. Duljina vodiča na koji djeluje sila iznosi
3 cm, a struja kroz njega 0,5 A. Silnice magnetskoga polja okomite su na vodič.
Koliki je iznos sile kojom magnetsko polje magneta djeluje na vodič?
F = mN
35.1.
Na vodič u magnetskom polju, kojim prolazi struja, djeluje sila. Tu silu zovemo Amperèova sila.
35.2.
Primijenimo pravilo desnog dlana.
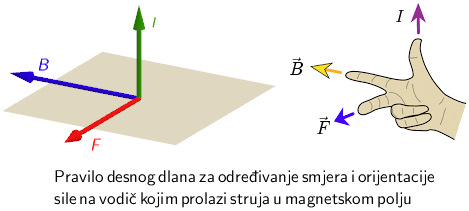
Ako palac desne ruke postavimo u smjer struje, ispružene prste u smjer magnetskog polja, sila koja djeluje na vodič ima smjer okomito iz dlana.
35.3.
Iznos Ampereove sile, ako je vodič okomit na smjer magnetskog polja jednak je:
\[F_{\small{\textrm{A}}}=B\,I\,\ell\]
\[F_{\small{\textrm{A}}}=1,5\cdot 10^{-3}\,\textrm{N}\]