Ljetni rok 2013. godine
1. zadatak
Prikazani su grafovi brzine u ovisnosti o vremenu za četiri gibanja.
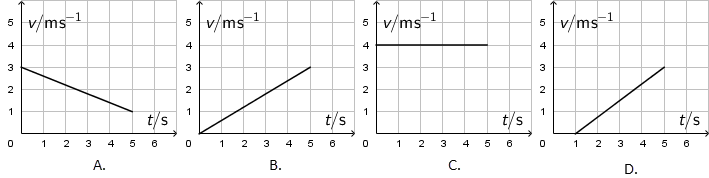
Koji od grafova prikazuje gibanje s akceleracijom najvećeg iznosa?
- A. Graf A.
- B. Graf B.
- C. Graf C.
- D. Graf D.
Kako iz \(v,t\) grafa određujemo akceleraciju?
Iz \(v,t\) grafa akceleraciju odredimo kao nagib pravca:
\[a=\frac{\Delta v}{\Delta t}.\]
Iz priloženih grafova vidimo da najveći nagib odgovara pravcu na grafu D.
Akceleracija je jednaka
\[a=\frac{\Delta v}{\Delta t}=0,75\,\textrm{m}/\textrm{s}^{2}\]
2. zadatak
Krenuvši iz mirovanja automobil se giba jednoliko ubrzano, te nakon 10 s postigne brzinu 20 m/s.
Sljedećih se 10 s automobil giba jednoliko brzinom koju je imao na kraju desete sekunde.
Kolika je srednja brzina automobila za tih 20 s gibanja?
- A. 10 m/s
- B. 15 m/s
- C. 20 m/s
- D. 30 m/s
Pomoć potražite na poveznicama
Prijeđeni put za vrijeme jednoliko ubrzanog gibanja jednak je: \[s_{1}\ =\frac{v\,t}{2}=100\,\textrm{m}\] Za vrijeme jednolikog gibanja automobil prijeđe put: \[s_{2}=v\,t=200\,\textrm{m}\] Ukupni prijeđeni put jednak je: \(s_{1}+s_{2}=300\,\textrm{m}\). Srednja brzina jednaka je: \[\overline{v}=\frac{s_{1}+s_{2}}{t}=\frac{300}{20}=15\,\textrm{m}/\textrm{s}\]
3. zadatak
Tijelo leži na vodoravnoj podlozi. Za tijelo zavežemo nit, kojom ga vučemo po podlozi. U jednom trenutku nit se prekine.
Što je od navedenoga točno? Zanemarite trenje.
- A. Tijelo se trenutačno zaustavi.
- B. Tijelo se nastavi gibati usporeno.
- C. Tijelo se nastavi gibati jednoliko.
- D. Tijelo se nastavi gibati ubrzano.
Trenje je zanemareno. Primijenite prvi Newtonov zakon.
Budući da je trenje zanemareno, nakon što se nit prekine na tijelo ne djeluje niti jedna sila i ono se, na osnovu prvog Newtonovog zakona, nastavlja gibati jednoliko po pravcu.
4. zadatak
Tijelo mase m pada s visine h. Početna brzina tijela je nula. Tijelo o tlo udari brzinom
v.
Koliko se pri tome mehaničke energije pretvorilo u druge oblike energije?
- A. \(m\,g\,h\)
- B. \(m\,v^{2}/2\)
- C. \(m\,g\,h+m\,v^{2}/2\)
- D. \(m\,g\,h-m\,v^{2}/2\)
Primijenite zakon očuvanja mehaničke energije.
Početna energija je u obliku potencijalne energije: \[E_{1}=m\,g\,h\] U trenutku pada na tlo tijelo ima kinetičku energiju: \[E_{2}=m\,v^{2}/2\] Kada bi sustav bio zatvoren, te bi dvije energije bile bi jednake. Zakon očuvanja energije možemo zapisati kao: \[E_1\ =E_2\ +\Delta E\] \(\Delta E\) je dio mehaničke energije koji se pretvorio u druge oblike: \[\Delta E=E_{1}–E_{2}=m\,g\,h-m\,v^{2}/2\]
5. zadatak
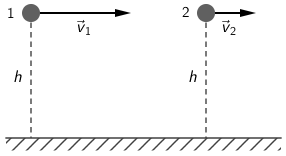
Dva jednaka tijela, 1 i 2, bačena su vodoravno s jednake visine. Iznos početne brzine tijela 1, \(v_{1}\), veći je od iznosa početne brzine tijela 2, \(v_{2}\).
Vrijeme trajanja pada tijela 1 označeno je s \(t_{1}\), a tijela 2 s \(t_{2}\). Domet tijela 1 je označen s \(D_{1}\), a tijela 2 je označen s \(D_{2}\).
Koja je od navedenih tvrdnji točna?
- A. \(D_{1} < D_{2}; t_{1} < t_{2}\)
- B. \(D_{1} = D_{2}; t_{1} = t_{2}\)
- C. \(D_{1} > D_{2}; t_{1} > t_{2}\)
- D. \(D_{1} > D_{2}; t_{1} = t_{2}\)
Pomoć potražite na poveznici Horizontalni hitac.
Ako primijenimo princip neovisnosti gibanja, zaključit ćemo da je put u vertikalnom smjeru (slobodni pad) jednak: \[h=g\,t^{2}/2\] Vrijeme za koje tijelo padne na tlo: \[t=\sqrt{\frac{2\,h}{g}}\qquad(1)\] Put u horizontalnom smjeru (jednoliko gibanje) jednak je: \[D=v_{0}\,t\qquad(2)\] Iz izraza (1) zaključujemo da će oba tijela jednako dugo padati (oba tijela padaju s jednake visine), a iz izraza (2) zaključujemo da će domet prvog tijela biti veći jer je domet proporcionalan početnoj brzini, a iz crteža je vidljivo da je početna brzina prvog tijela veća. Točan odgovor je D.
6. zadatak
U posudi se nalazi plin na temperaturi 27 0C i tlaku
p0. Plin izohorno zagrijemo na temperaturu
327 0C.
Koliki je tlak plina nakon zagrijavanja?
- A. 0,5 p0
- B. p0
- C. 2 p0
- D. 4 p0
Pomoć potražite na poveznici Izohorna promjena stanja plina.
Jednadžbu stanja idealnog plina možemo zapisati kao: \[\frac{p\,V}{T}=\frac{p_{0}\,V_{0}}{T_{0}}\] Za izohorne procese volumen plina je konstantan \(\left (V=V_{0}\right )\) pa jednadžbu stanja plina prikazujemo kao: \[\frac{p}{T}=\frac{p_{0}}{T_{0}}\] Za tlak plina dobijemo: \[p=\frac{p_{0}\,T}{T_{0}}\] Nakon što temperature pretvorimo u kelvine, dobijemo: \[p=2\,p_{0}\]
7. zadatak
Tri tijela jednakih masa imaju specifične toplinske kapacitete za koje vrijedi: \(c_{1} = 2\,c_{2} = 3\,c_{3}\). Dok su u termičkom kontaktu,
ukupno svim tijelima zajedno dovede se toplina iznosa \(11\,Q\). Tijelo specifičnog toplinskog kapaciteta \(c_{2}\) pri tome primi topline \(3\,Q\).
Koliko je topline \(Q_{1}\) primilo tijelo specifičnog toplinskog kapaciteta \(c_{1}\), a koliko topline \(Q_{3}\), tijelo specifičnog toplinskog
kapaciteta \(c_{3}\)?
- A. \(Q_{1}=2\,Q,Q_{3}=6\,Q\)
- B. \(Q_{1}=3\,Q,Q_{3}=5\,Q\)
- C. \(Q_{1}=5\,Q,Q_{3}=3\,Q\)
- D. \(Q_{1}=6\,Q,Q_{3}=2\,Q\)
Količina topline koju tijelo zagrijavanjem primi ili hlađenjem preda jednaka je: \[Q=m\,c\,\Delta t\]
Tijela su primila topline: \[Q_{1}=m\,c_{1}\,\Delta t\] \[Q_{2}=m\,c_{2}\,\Delta t=m\,c_{1}\,\Delta t/2\] \[Q_{3}=m\,c_{3}\,\Delta t=m\,c_{1}\,\Delta t/3\] Promjena temperature sva tri tijela jednaka je jer su ona i dalje u termičkom kontaktu pa su poprimila jednake konačne temperature. Poznato je da je drugo tijelo primilo toplinu \(3\,Q\): \[m\,c_{1}\,\Delta t/2=3\,Q\] Iz ove jednadžbe odredimo \(m\,\Delta t\): \[m\,\Delta t=6\,Q/c_{1}\] Uvrstimo to u prvu i treću jednadžbu, pa dolazimo do rješenja: \[Q_{1}=6\,Q\,c_{1}/c_{1}=6\,Q\] \[Q_{3}=6\,Q\,c_{1}/3\,c_{1}=2\,Q\]
8. zadatak
Kalorimetar sadrži 400 g vode temperature 80 0C.
U kalorimetar s vodom dolijemo 1600 g vode temperature 40 0C.
Koliko iznosi temperatura termodinamičke ravnoteže? Zanemarite zagrijavanje kalorimetra i druge gubitke topline.
- A. 44 0C
- B. 48 0C
- C. 58 0C
- D. 64 0C
Toplina koju tijelo zagrijavanjem prima ili hlađenjem predaje jednaka je: \[Q=m\,c\,\Delta t\] Ako je sustav izoliran, toplina je očuvana, a to znači da je toplina koju predaje toplije tijelo jednaka toplini koju hladnije tijelo primi.
Temperatura toplinske ravnoteže bit će između \(40\,^{0}\textrm{C}\) i \(40\,^{0}\textrm{C}\). Tu temperaturu označimo s \(t_{\textrm{kon}}\). Toplija voda preda toplinu: \[Q_{1}=m_{1}\,c\,\left(t_{1}\ -t_{\textrm{kon}}\right)\] Hladnija voda primi toplinu: \[Q_{2}=m_{2}\,c\,\left (t_{\textrm{kon}}–t_{2}\right )\] Te dvije topline moraju biti jednake: \[m_{1}\,c\,\left(t_{1}-t_{\textrm{kon}}\right)=m_{2}\,c\,\left (t_{\textrm{kon}}–t_{2}\right )\] Podijelimo cijelu jednadžbu s \(c\), riješimo se zagrada i uvrstimo zadane podatke: \[0,4·80-0,4·t_{\textrm{kon}}=1,6·t_{\textrm{kon}}-1,6·40\] Za rješenje ove jednadžbe dobijemo: \[t_{\textrm{kon}}=48\,^{0}\textrm{C}\]
9. zadatak
Atom helija sastoji se od elektronskog omotača s dva elektrona i jezgre koja sadrži dva protona i dva neutrona.
Koliko iznosi električni naboj opisanog atoma helija, \(Q_{\small{\textrm{A}}}\), a koliko električni naboj jezgre atoma helija, \(Q_{\small{\textrm{J}}}\)?
U odgovorima \(e\) označava elementarni naboj.
- A. \(Q_{\small{\textrm{A}}} = –2\,e, Q_{\small{\textrm{J}}} = 0\)
- B. \(Q_{\small{\textrm{A}}} = –2\,e, Q_{\small{\textrm{J}}} = +2\,e\)
- C. \(Q_{\small{\textrm{A}}} = 0, Q_{\small{\textrm{J}}} = +2\,e\)
- D. \(Q_{\small{\textrm{A}}} = +2\,e, Q_{\small{\textrm{J}}} = 0\)
Što se događa s elektronima ako prvoj kugli primaknemo negativno nabijeni štap? Uzmite u obzir da se kugle dodiruju.
Atom helija ima dva elektrona i dva protona u jezgri. Prema tome, električni naboj atoma jednak je nuli, a naboj jezgre jednak je naboju dva protona, odnosno, +2 e.
10. zadatak
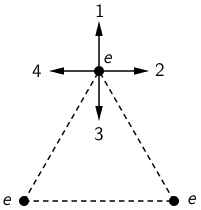
Tri elektrona su razmještena tako da zatvaraju jednakostranični trokut, kao što je prikazano na crtežu. Koja strjelica označava vektor rezultantne elektrostatske sile na elektron u gornjem vrhu trokuta?
- A. strjelica 1
- B. strjelica 2
- C. strjelica 3
- D. strjelica 4
Primijenite Coulombov zakon: \[F=k\frac{Q_{1}Q_{2}}{r^{2}}\] Više o električnoj sili između dva točkasta naboja možete saznati na poveznici Električna sila.
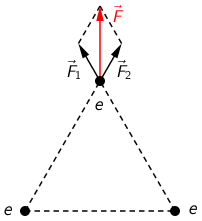
Električne sile kojima elektroni djeluju na elektron u gornjem vrhu trokuta označene su crno obojenim vektorima. Ukupnu silu možemo odrediti pomoću pravila paralelograma, i ona je označena crveno obojenim vektorom.
11. zadatak
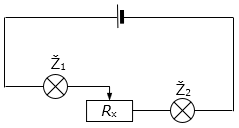
Na izvor istosmjernog napona serijski su spojene žaruljice Ž1 i
Ž2 te promjenjivi otpornik, kao što je prikazano na crtežu.
Što će se od navedenog dogoditi s intenzitetima svjetlosti žaruljica kad se promjenjivom otporniku poveća otpor
Rx?
- A. Intenziteti svjetlosti Ž1 i Ž2 će se smanjiti.
- B. Intenzitet svjetlosti Ž1 će se smanjiti, a Ž2 povećati.
- C. Intenzitet svjetlosti Ž1 će se povećati, a Ž2 smanjiti.
- D. Intenziteti svjetlosti Ž1 i Ž2 će se povećati.
Rad, odnosno energiju električne struje možemo prikazati kao: \[W=UIt\]
Žarulje i otpornik spojeni su serijski. Povećanjem otpora Rx povećava se ukupni otpor kruga. Na osnovu Ohmovog zakona zaključujemo da će se struja kroz žarulje smanjiti, pa će one svijetliti slabije.
12. zadatak
Elektron ulijeće u homogeno magnetsko polje, okomito na silnice polja.
Što se događa s brzinom elektrona dok se giba u magnetskom polju?
- A. brzini se mijenjaju smjer i iznos
- B. brzina ostaje nepromijenjena
- C. brzini se mijenja smjer, a po iznosu je stalna
- D. brzina je po smjeru stalna, a mijenja joj se iznos
Pomoć potražite na poveznici Gibanje naboja u magnetskom polju.
Sila koja djeluje na elektron može se prikazati kao \(F=e\,v\,B\) i uvijek mora biti okomita na vektore \(\vec{v}\) i \(\vec{B}\). To je moguće samo ako je putanja kružnica.
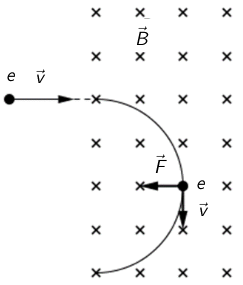
Elektron se giba jednoliko po kružnici pa se iznos brzine ne mijenja. Mijenjaju se samo pravac (smjer) i orijentacija brzine.
13. zadatak
Jednostavno njihalo otklonjeno je iz ravnotežnog položaja kao što je prikazano na crtežu i pušteno. Njihalo izvodi harmonijsko titranje.
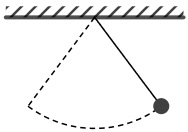
Koji graf prikazuje ukupnu silu koja uzrokuje harmonijsko titranje tog njihala tijekom jednog perioda titranja počevši od trenutka kad je pušteno?
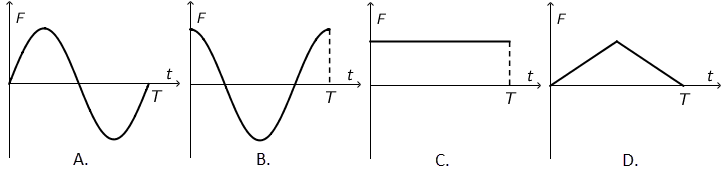
- A. graf A.
- B. graf B.
- C. graf C.
- D. graf D.
Pomoć potražite na poveznici Titranje matematičkog njihala.
Silu koja uzrokuje gibanje matematičkog ili jednostavnog njihala možemo prikazati kao \[F=k\,x\] Elongacija njihala mijenja se kao \[x=x_{0}\,\textrm{cos}\,\omega\,t\] jer tijelo u početnom trenutku ima maksimalnu elongaciju \(x_{0}\). Kružna frekvencija označena je s \(\omega\). Silu možemo prikazati kao \[F=k\,x_{0}\,\textrm{cos}\,\omega\,t\] što odgovara grafu na crtežu B jer sila u početnom trenutku ima maksimalnu vrijednost \[F=F_{0}\,\textrm{cos}\,\omega\,t\]
14. zadatak
Čovjek visok 1,8 m stoji uspravno ispred ravnog zrcala u kojem se vidi u cijelosti.
Kakva je slika čovjeka u zrcalu?
- A. realna, visoka 1,8 m
- B. virtualna, visoka 1,8 m
- C. realna, viša od 1,8 m
- D. virtualna, viša od 1,8 m
Pomoć potražite na poveznici Ravno zrcalo.
Ravno zrcalo daje virtualnu i uspravnu sliku koja je jednako visoka kao i predmet.
15. zadatak
Koliko vremena treba radiosignalu da prijeđe udaljenost od 250 m u vakuumu?
- A. 8,3·10-7 s.
- B. 1,2·10-6 s.
- C. 2,4·106 s.
- D. 7,5·1010 s.
Ako se elongacija kod harmonijskog titranja mijenja kao: \[y=y_{0}\,\textrm{sin}\,\omega\, t\] onda se brzina mijenja kao: \[v=v_{0}\,\textrm{cos}\,\omega\, t\] Više o nastanku vala na užetu potražite na poveznici Nastanak transverzalnog vala.
Radiosignal se u vakuumu širi brzinom svjetlosti 3·108 m/s pa je vrijeme potrebno da signal prijeđe udaljenost od 250 m jednako: \[t=\frac{s}{c}=8,3\cdot 10^{-7}\,\textrm{s}\]
16. zadatak
Youngovim pokusom s monokromatskom svjetlošću dobivaju se interferentne pruge na zastoru.
Što treba učiniti da se samo jednom od navedenih promjena poveća razmak između inteferentnih pruga?
- A. smanjiti razmak između pukotina
- B. povećati razmak između pukotina
- C. smanjiti razmak između zastora i pukotina
- D. koristiti svjetlost manje valne duljine
Pomoć potražite na poveznici Youngov pokus.
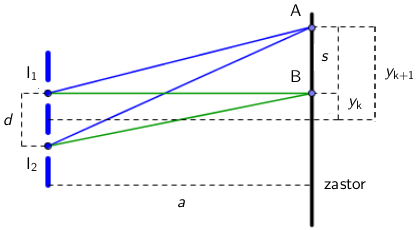
Udaljenost k-te svijetle pruge od središta zastora je: \[y_{\textrm{k}}=\frac{k\,\lambda\,a}{d}\] Udaljenost između dvije susjedne svijetle pruge je: \[s=y_{\textrm{k}+1}-y_\textrm{k}=\frac{\lambda\,a}{d}\] Razmak između pruga možemo povećati ako:
- Povećamo valnu duljinu svjetlosti
- Povećamo razmak između pukotina i zastora
- Smanjimo udaljenost između pukotina
17. zadatak
Tijelo harmonijski titra ovješeno na oprugu konstante elastičnosti 0,2 N/m. Kinetička energija pri prolasku kroz
ravnotežni položaj iznosi 2,5·10-4 J.
Kolikom amplitudom titra ovo tijelo? Zanemarite gubitke energije.
- A. 1,3 cm
- B. 2,5 cm
- C. 5,0 cm
- D. 7,5 cm
Pomoć potražite na poveznici Pretvorbe energije pri harmonijskom titranju.
U ravnotežnom položaju potencijalna energija jednaka je nuli pa je ukupna energija jednaka kinetičkoj energiji, koja je tada maksimalna: \[E_{1}=E_{\textrm{k,maks}}\] U krajnjem položaju kinetička energija jednaka je nuli jer tijelo zastane pa je ukupna energija jednaka potencijalnoj, koja je tada najveća: \[E_{2}=E_{\textrm{p,maks}}\] Prema zakonu očuvanja energije te su dvije energije jednake: \[E_{1}=E_{2}\] \[E_{\textrm{p,maks}}=E_{\textrm{k,maks}}\] Maksimalna potencijalna energija jednaka je: \[E_{\textrm{p,maks}}=\frac{1}{2}\,k\,x_{0}^{2}\] Ako ovaj izraz izjednačimo s kinetičkom energijom u ravnotežnom položaju, za amplitudu titranja dobijemo: \[x_{0}=\sqrt{\frac{2\,E_{\textrm{k,maks}}}{k}}=5\,\textrm{cm}\]
18. zadatak
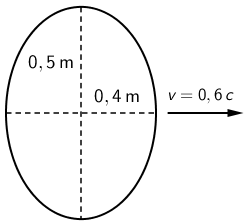
Ispred promatrača na Zemlji prolazi svemirski brod brzinom 0,6 c. S bočne strane broda
nalazi se okno. Promatrač na brodu vidi da je okno kružno, polumjera 0,5 m.
Kakvo okno na brodu vidi promatrač sa Zemlje? Brzina svjetlosti u vakuumu je c.
- A. kružno, polumjera 0,4 m
- B. kružno, polumjera 0,5 m
- C. eliptično, s velikom poluosi 0,5 m položenoj okomito na smjer gibanja broda
- D. eliptično, s velikom poluosi 0,5 m položenoj u smjeru gibanja broda
Pomoć potražite na poveznici Kontrakcija duljine.
Dimenzije tijela u smjeru gibanja se skraćuju za faktor \[\sqrt{1-v^{2}/c^{2}}\] Ovo nazivamo kontrakcijom (skraćenjem) duljine. Skratit će se polumjer okna u smjeru gibanja tako da će za promatrača na Zemlji on iznositi: \[L=L_{0}\sqrt{1-v^{2}/c^{2}}=0,4\,\textrm{m}\] Polumjer koji je okomit na smjer gibanja neće se skratiti.
19. zadatak
Pri temperaturi 3000 K neko tijelo zrači maksimalnim intenzitetom zračenje valne duljine 963 nm.
Pri kojoj će temperaturi to tijelo imati maksimum zračenja na valnoj duljini 321 nm?
- A. 1000 K
- B. 3000 K
- C. 6000 K
- D. 9000 K
Pomoć potražite na poveznici Wienov zakon.
Prema Wienovom zakonu, valna duljina pri kojoj crno tijelo zrači najviše energije obrnuto je proporcionalna apsolutnoj temperaturi tijela koje zrači: \[\lambda_\textrm{maks}\cdot T= b\] gdje je \(b\) Wienova konstanta. Napišimo ovaj zakon za oba tijela: \[\lambda_\textrm{maks,1}\cdot T_{1}= b\] \[\lambda_\textrm{maks,2}\cdot T_{2}= b\] Budući da su desne strane ovih jednadžbi jednake, moraju biti i lijeve strane pa za temperaturu drugog tijela dobijemo: \[T_{2}=\frac{\lambda_\textrm{maks,1}\cdot T_{1}}{\lambda_\textrm{maks,2}}=9000\,\textrm{K}\]
20. zadatak
Putnik iz svemirskog broda, koji napušta Zemlju brzinom 0,8 c, pošalje laserski signal
prema Zemlji.
Kolika je brzina laserskog signala u odnosu na putnika u brodu \(\left(v_{1}\right)\), a kolika u odnosu na Zemlju \(\left(v_{2}\right)\)?
Brzina svjetlosti u vakuumu je c.
- A. v1 = 0,2 c i v2 = 0,2 c
- B. v1 = 0,2 c i v2 = 0,8 c
- C. v1 = 0,8 c i v2 = 0,2 c
- D. v1 = c i v2 = c
Pomoć potražite na poveznici Zbrajanje brzina.
Brzina svjetlosti u svim inercijskim sustavima je konstantna. Laserski signal također se giba brzinom svjetlosti pa je njegova brzina jednaka i za putnika u brodu i za promatrača na Zemlji.
21. zadatak
Jezgra kisika ima oznaku \(_{\;8}^{17}\,\textrm{O}\).
Koliko nukleona sadrži ova jezgra kisika?
- A. 8
- B. 9
- C. 17
- D. 25
Više o zakonu radioaktivnog raspada možete saznati na poveznici Zakon radioaktivnog raspada
U zapisu jezgre nekog kemijskog elementa \[_Z^{A}\,\textrm{X}\] \(A\) označava broj nukleona u jezgri \(\left(A=Z+N;\textrm{broj protona i neutrona}\right)\). Prema tome, u jezgri ima 17 nukleona i to 8 protona i 9 neutrona.
22. zadatak
Rukom se udari po stolu.
Kakav je iznos sile kojom ruka djeluje na stol?
- A. manji od iznosa sile kojom stol djeluje na ruku
- B. jednak iznosu sile kojom stol djeluje na ruku
- C. veći od iznosa sile kojom stol djeluje na ruku
Više o složenom gibanju i hicima možete saznati na poveznici Složena gibanja - hici. Podignite tijelo na neku visinu, vektor brzine postavite horizontalno i pokrenite animaciju. Zabilježite koliko je vremena tijelo padalo. Vratite animaciju na početak i pomoću klizača postavite brzinu na nulu (slobodni pad). Pokrenite annimaciju i zabilježite potrbno vrijeme. Što zaključujete?
Sila kojom ruka udari stol po iznosu je jednaka sili kojom stol djeluje na ruku. (Treći Newtonov zakon.) Obje sile imaju jednak smjer (leže na istom pravcu) i imaju suprotnu orijentaciju.
23. zadatak
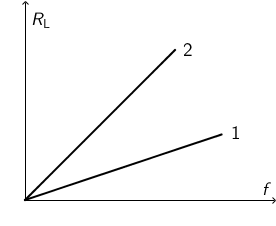
Crtež prikazuje dijagram induktivnog otpora \(R_{\small{\textrm{L}}}\) dviju zavojnica, 1 i 2, u ovisnosti o frekvenciji \(f\) izmjenične struje koja
prolazi zavojnicama. \(L_{1}\) označava induktivitet zavojnice 1, \(L_{2}\) zavojnice 2.
Koji je odnos između tih induktiviteta?
- A. \(L_{1} < L_{2}\)
- B. \(L_{1} = L_{2}\)
- C. \(L_{1} > L_{2}\)
Pomoć potražite na poveznici Induktivni otpor.
Induktivni otpor ovisi o induktivitetu zavojnice, \(L\), i kružnoj frekvenciji, \(\omega=2\,\pi\,f\), a može se prikazati kao:
\[R_{\small{\textrm{L}}}=L\,\omega=2\,\pi\,f\,L\]
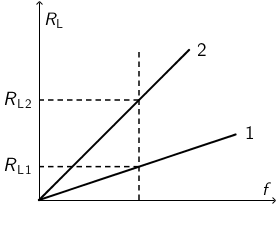
Iz crteža vidimo da za istu frekvenciju zavojnici 2 odgovara veći induktivni otpor pa je zbog toga njezin induktivitet veći.
24. zadatak
Kojim radioaktivnim zračenjem jezgra ne mijenja svoj broj protona?
- A. \(\alpha\)
- B. \(\beta\)
- C. \(\gamma\)
Pomoć potražite na poveznici Radioaktivnost
Alfa zračenje prikazujemo jednadžbom: \[_{Z}^{A}\textrm{X}\rightarrow _{2}^{4}\textrm{He}+\,_{Z-2}^{A-4}\textrm{Y}\] Beta zračenje prikazujemo jednadžbom: \[_{Z}^{A}\textrm{X}\rightarrow _{-1}^{\;\;0}\textrm{e}+\,_{Z+1}^{\;\;\;A}\textrm{Y}\] Gama zračenje prikazujemo jednadžbom: \[_{Z}^{A}\,\textrm{X}^{*}\rightarrow \gamma+\,_{Z}^{A}\textrm{X}\] Vidimo da se samo kod gama zračenja ne mijenja \(Z\), dakle ni broj protona u jezgri.
25. zadatak
Čestica kruži po stazi polumjera 0,1 m brzinom 9,6·104 m/s.
Kolika je frekvencija kruženja čestice?
Odgovor: Hz
Pomoć potražite na poveznici Jednoliko kružno gibanje.
Brzina tijela koje se giba jednoliko po kružnici: \[v=\frac{2\,r\,\pi}{T}\] Frekvencija je jednaka recipročnoj vrijednosti ophodnog vremena: \[f=\frac{1}{T}\] Iz ove dvije jednadžbe za frekvenciju dobijemo: \[f=\frac{v}{2\,r\,\pi}=152789\,\textrm{Hz}=1,53\cdot 10^{5}\,\textrm{Hz}\]
26. zadatak
Na kojoj visini iznad površine Zemlje akceleracija sile teže iznosi 7,33 m/s2?
Masa Zemlje je 6·1024 kg,
a polumjer 6,4·106 m6,4·106 m.
Odgovor: km
Pomoć potražite na poveznici Opći zakon gravitacije.
Sila teža: \[F_{\textrm{g}}=G\,\frac{M\,m}{\left(R+h\right)^2}\] Na osnovu drugog Newtonovog zakona silu težu možemo prikazati kao: \[F_{\textrm{g}}=m\,g\Rightarrow g=\frac{F_{\textrm{g}}}{m}\] Akceleracija sile teže jednaka je: \[g=G\,\frac{M}{\left(R+h\right)^2}\] Iz ove jednadžbe dobijemo: \[R+h=\sqrt{G\,\frac{M}{g}}\] Tražena visina je: \[h=\sqrt{G\,\frac{M}{g}}-R=989\,\textrm{m}\]
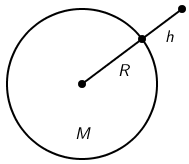
27. zadatak
Na temperaturi 600 0C duljina bakrene žice je 60 m.
Kolika je duljina te žice na temperaturi 0 0C? Linearni koeficijent termičkog rastezanja bakra je
1,7·10-5 K-1.
Odgovor: m
Pomoć potražite na poveznici Linearno toplinsko širenje čvrstih tijela.
Iz jednadžbe \[\ell=\ell_{0}\,\left(1+\alpha\,\Delta t\right)\] dobijemo: \[\ell_{0}=\frac{\ell}{1+\alpha\,\Delta t}=59,39\,\textrm{m}\]
28. zadatak
Zavojnica je spojena na izvor napona \(u=\left ( 220\,\sqrt{2}\,\textrm{V} \right )\,\textrm{sin}\left ( 314\,t\,\textrm{s}^{-1} \right ) \).
Zavojnicom prolazi maksimalna struja \(2\,\sqrt{2}\,\textrm{A}\).
Kolika je impedancija strujnog kruga?
Odgovor: \(\Omega\)
Pomoć potražite na poveznici Serijski RCL krug.
Impedancija (ukupni otpor u krugu izmjenične struje): \[Z=\frac{U_{0}}{I_{0}}\] Maksimalni napon pročitamo iz zadane jednadžbe: \[U_{0}=220\,\sqrt 2\,\textrm{V}\] Maksimalna struja je zadana: \[I_{0}=2\,\sqrt 2\,\textrm{A}\] Impedancija je jednaka: \[Z=\frac{220\,\sqrt 2}{2\,\sqrt 2}=110\,\Omega\]
29. zadatak
29. Konvergentna leća L1, žarišne udaljenosti iznosa 20 cm i divergentna leća L2, žarišne udaljenosti iznosa 5 cm, nalaze se u zraku. Leće su razmještene kao što je prikazano na crtežu.
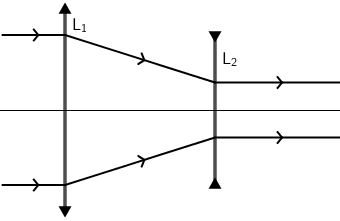
Na tako postavljene leće pada paralelni snop svjetlosti usporedno s optičkom osi leća. Nakon prolaska kroz obje leće snop svjetlosti ostaje paralelan
i usporedan optičkoj osi leća.
Kolika je udaljenost između leća L1 i L2?
Odgovor: cm
Pomoć potražite na poveznici Sabirne i rastresne leće.
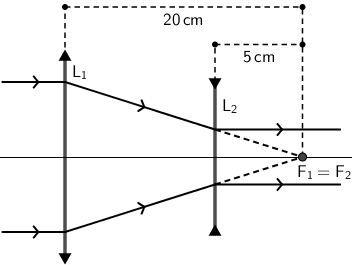
Da bi ovo bilo moguće, žarišta obje leće moraju se nalaziti u istoj točki. Iz crteža vidimo da je udaljenost između leća jednaka 15 cm.
30. zadatak
Vrijeme poluraspada nekog radioaktivnog uzorka je 28 dana.
Za koje se vrijeme raspadne 7/8 početne količine tog uzorka?
Odgovor: dana
Pomoć potražite na poveznici Zakon radioaktivnog raspada.
Broj jezgri koje se raspadnu nakon vremena \(t\) jednak je: \[\Delta N=N_{0}-N=\frac{7}{8}\,N_{0}\] Iz ove jednadžbe dobijemo da je broj neraspadnutih jezgri nakon vremena \(t\) jednak: \[N=\frac{1}{8}\,N_{0}\] Uvrstimo to u zakon radioaktivnog raspada: \[N=N_{0}\,2^{-\frac{t}{T}}\] \[\frac{1}{8}\,N_{0}=N_{0}\,2^{-\frac{t}{T}}\] Podijelimo jednadžbu s \(N_{0}\), a 1/8 prikažimo kao \(2^{-3}\): \[2^{-3}=2^{-\frac{t}{T}}\] Rješenje je: \[t=3\,T=84\,\textrm{dana}\] Zadatak smo mogli riješiti i ovako: nakon vremena \(T\) preostane \(N_{0}/2\) jezgara, nakon \(2\,T\) preostane \(N_{0}/4\) jezgri i nakon \(3\,T\) preostane \(N_{0}/8\) jezgri, što znači da se raspalo \(7\,N_{0}/8\). \[t=3\,T=84\,\textrm{dana}\]
31. zadatak
Kamen mase 15 kg spustimo u vodu.
Koliko iznosi rezultantna sila na kamen dok tone, kada je cijelim obujmom ispod površine vode (kao što je prikazano na crtežu) prije nego dotakne dno?
Gustoća kamena je 2500 kg m-3,
a vode 1000 kg m-3. Zanemarite viskoznost vode.

Odgovor: N
Pomoć potražite na poveznici Sila na uronjeno tijelo-uzgon.
Sila teža usmjerena je vertikalno prema dolje, a uzgon vertikalno prema gore.
Rezultanta sile teže i uzgona jednaka je:
\[F=F_{\textrm{g}}-F_\textrm{u}=m_{\textrm{kamen}}\,g-\rho_{\textrm{voda}}\,g\,V_{\textrm{kamen}}\]
Volumen kamena izrazimo pomoću njegove mase i gustoće:
\[V_{\textrm{kamen}}=\frac{m_{\textrm{kamen}}}{\rho_{\textrm{kamen}}}\]
Za rezultantnu silu dobijemo:
\[F=m_{\textrm{kamen}}\,g-\rho_{\textrm{voda}}\,g\,\frac{m_{\textrm{kamen}}}{\rho_{\textrm{kamen}}}\]
Izlučimo zajednički faktor pa za rezultantnu silu dobijemo:
\[F=\left(1-\frac{\rho_{\textrm{voda}}}{\rho_{\textrm{kamen}}}\right)\,m_{\textrm{kamen}}\,g=90\,\textrm{N}\]
32. zadatak
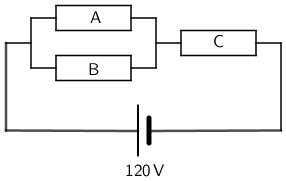
U krug istosmjerne struje napona 120 V uključena su tri jednaka otpornika, A, B i C, kao što je prikazano na crtežu.
Odredite napon na krajevima svakog otpornika.
Odgovor: V
U polje za odgovor unesite napon na otporniku A, B i C odvojen zarezom, npr. 10, 20, 30.
Pomoć potražite na poveznici Spajanje otpornika.
Sva su tri otpora jednaka. Označimo ih s \(R_{0}\). \[R_{0}=R_{\textrm{A}}=R_{\textrm{B}}=R_{\textrm{C}}\] Otpori A i B spojeni su paralelno pa njihov otpor dobijemo iz: \[\frac{1}{R_{\textrm{AB}}}=\frac{1}{R_{\textrm{A}}}+\frac{1}{R_{\textrm{B}}}\] \[R_{\textrm{AB}}=\frac{R_{0}}{2}\] Ukupni je otpor jednak: \[R=R_{\textrm{AB}} + R_{\textrm{C}}=\frac{3\,R_{0}}{2}\] Ukupni je napon jednak: \[U=I\,R=\frac{3\,I\,R_{0}}{2}\] Iz posljednje jednadžbe dobijemo: \[I\,R_{0}=\frac{2\,U}{3}=80\,\textrm{V}\] To je napon na krajevima otpora C: \[U_{\textrm{C}}=80\,\textrm{V}\] Napon na krajevima otpora \(R_{\textrm{AB}}\) jednak je: \[U_{\textrm{AB}}\ =I\,R_{\textrm{AB}}=\frac{I\,R_{0}}{2}=40\,\textrm{V}\] Budući da su otpori A i B spojen i paralelno, napon na njihovim krajevima je jednak i iznosi 40 V: \[U_{\textrm{A}}=40\,\textrm{V}\] \[U_{\textrm{B}}=40\,\textrm{V}\]
33. zadatak
Ako se idealnome plinu dovede 3000 J topline, plin prijeđe iz stanja A u stanje B kao što je prikazano na crtežu.
Kolika je promjena unutarnje energije plina?
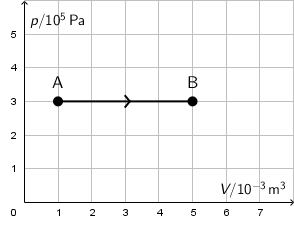
Odgovor: J
Pri izobarnom širenju plin obavi rad: \[W=p\,\Delta V\] Primijenite prvi zakon termodinamike.
Pri prijelazu plina iz stanja A u stanje B plin izvrši rad: \[W=p\,\Delta V=p\,\left(V_{2}-V_{1}\right)=3\cdot10^{5}\cdot 4\cdot 10^{-3}=1200\,\textrm{J}\] Prema prvom zakonu termodinamike, toplina dovedena sustavu dijelom se pretvara u unutarnju energije sustava, a dijelom u rad kojeg sustav obavlja: \[Q=\Delta U+W\] Za promjenu unutarnje energije sustava dobijemo: \[\Delta U=Q-W=1800\,\textrm{J}\]
34. zadatak
Paralelni snop svjetlosti valne duljine 600 nm pada okomito na optičku rešetku. Optička rešetka ima 400 pukotina na svaki milimetar duljine.
Vidi li se na ogibnoj slici svijetla pruga petog reda?
Odgovor:
Pomoć potražite na poveznici Ogib svjetlosti na optičkoj rešetki.
Iz jednadžbe za optičku rešetku: \[d\,\textrm{sin}\,\alpha = k\,λ\] za redni broj svijetle pruge, \(k\), dobijemo \[k=\frac{d\,\textrm{sin}\,\alpha}{λ}\] Broj \(k\) će biti najveći ako je \(\alpha=90^{0}\). \[k_{\textrm{maks}}\le\frac{d}{\lambda}\] Odredimo konstantu optičke rešetke: \[d=\frac{1}{400}\,\textrm{mm}=2,5\cdot 10^{-6}\,\textrm{m}\] Izračunajmo najveći k: \[k_{\textrm{maks}}\le\frac{d}{\lambda}=4,17\] Broj \(k\) je cijeli broj pa je njegova najveća vrijednost jednaka 4.
35. zadatak
Intenzitet Sunčeva elektromagnetskoga zračenja na udaljenosti od 1,5·1011 m od središta Sunca
iznosi 1400 W/m2.
Koliki je polumjer Sunca? Uzmite da je Sunce oblika kugle i da zrači kao crno tijelo temperature \(6000\,\textrm{K}\).
Napomena: površina sfere polumjera \(R\) određuje se preko izraza \(S=4\,r^{2}\,\pi\).
Odgovor: m
Pomoć potražite na poveznici Stefan-Boltzmannov zakon.
Snaga zračenja Sunca (Stefan-Boltzmannov zakon): \[P=\sigma\,S\,T^{4}\] Energija zračenja Sunca širi se u prostor obuhvaćen površinom sfere polumjera \(r\): \[S=4\,r^{2}\,\pi\] Intenzitet zračenja na udaljenosti \(r\) od Sunca: \[I=\frac{P}{4\,r^{2}\,\pi}\] Ako za snagu zračenja Sunca uvrstimo \(R\) (polumjer Sunca): \[P=\sigma S\,T^{4}=4\,R^{2}\,\pi\,\sigma T^{4}\] za intenzitet na tom mjestu dobijemo: \[I=\frac{\sigma\,R^{2}\,T^{4}}{r^{2}}\] Iz ove jednadžbe možemo odrediti polumjer Sunca: \[R=\frac{r}{T^{2}}\sqrt{\frac{I}{\sigma}}=6,5\cdot 10^{8}\,\textrm{m}\]