Probni ispit za maturu 2024. godine
1. zadatak
Koliki je iznos ubrzanja tijela u najvišoj točki putanje ako je izbačeno vertikalno uvis?
Zanemarite uzgon u zraku.
- A. Iznos je jednak nuli.
- B. Jednak je iznosu ubrzanja sile teže.
- C. Veći je od iznosa ubrzanja sile teže.
- D. Manji je od iznosa ubrzanja sile teže.
Tijelo bačeno vertikalno uvis nekom početnom brzinom giba se jednoliko usporeno, pri čemu se brzina smanjuje do nule. U tom je trenutku tijelo doseglo najveću visinu, nakon čega slobodno pada.
1. Tijelo se giba od mjesta s kojega je izbačeno prema gore
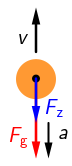
Na tijelo djeluje sila teža \(\vec{F_\textrm{g}}\) vertikalno prema dolje i otpor zraka \(\vec{F_\textrm{z}}\) također vertikalno prema dolje jer je
sila otpora zraka suprotne orijentacije od brzine.
Iznos akceleracija tijela je:
\[a=\frac{F_\textrm{g}+F_\textrm{z}}{m}\]
Orijentacija akceleracije suprotna je orijentaciji brzine pa je gibanje usporeno. Ovdje se ne radi o jednoliko usporenom gibanju jer se otpor zraka smanjuje ako
se smanjuje brzina pa se zbog toga smanjuje rezultantna sila na tijelo, a time i akceleracija.
2. Tijelo je dosegnulo najvišu točku

U najvišoj točki tijelo za trenutak zastane pa je otpor zraka jednak nuli. Iznos akceleracije tijela tada je: \[a=\frac{F_\textrm{g}+0}{m}=\frac{m\,g}{m}=g\] To je točan odgovor.
3. Tijelo se giba od najviše točke do mjesta iz kojega je izbačeno
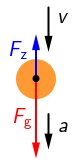
Na tijelo djeluje sila teža \(\vec{F_\textrm{g}}\) vertikalno prema dolje i otpor zraka \(\vec{F_\textrm{z}}\) vertikalno prema gore jer je
sila otpora zraka suprotne orijentacije od brzine.
Iznos akceleracija tijela je:
\[a=\frac{F_\textrm{g}-F_\textrm{z}}{m}\]
Orijentacija akceleracije jednaka je orijentaciji brzine pa je gibanje ubrzano. Ovdje se ne radi o jednoliko ubrzanom gibanju jer se otpor zraka povećava ako
se povećava brzina pa se zbog toga smanjuje rezultantna sila na tijelo, a time i akceleracija.
Napomena:
Načelno je moguće da se otpor zraka toliko poveća da postane jednak sili teži. Tada je ukupna sila jednaka nuli i tijelo padne na mjesto bacanja jednolikom brzinom,
koju nazivamo granična brzina.
2. zadatak
Kugle X i Y gibaju se jednoliko pravocrtno. Masa kugle X iznosi 1 kg i kugla se giba brzinom 2 m/s.
Masa kugle Y iznosi 2 kg i kugla se giba brzinom 3 m/s.
Koliki su iznosi sila FX i
FY, ako je
FX ukupna sila na kuglu X, a
FY ukupna sila na kuglu Y?
- A. FX = 0 N, FY = 0 N
- B. FX = 4 N, FY = 2 N
- C. FX = 2 N, FY = 3 N
- D. FX = 3 N, FY = 6 N
Primijenite 1. Newtonov zakon.
Oba se tijela gibaju jednoliko pravocrtno.
Ukupna sila na tijelo koje se giba jednoliko pravocrtno jednaka je nuli. Točan je odgovor A.
3. zadatak
Određeni uređaj obavi rad W1 za vrijeme
t1. Drugi uređaj, dva puta veće snage, obavi
rad W2 za vrijeme
t2.
Koja je od navedenih tvrdnja točna?
- A. Ako je t2 = 2t1, onda je W2 = 2W1.
- B. Ako je t2 = 2t1, onda je W2 = W1.
- C. Ako je t1 = 2t2, onda je W1 = W2.
- D. Ako je t1 = t2, onda je W1 = 2W2.
Snaga uređaja jednaka je radu obavljenom u jediničnom vremenu: \[P=\frac{W}{t}\] Napišite izraze snagu jednog i drugog uređaja i uzmite u obzir da drugi uređaj ima dva puta veću snagu: \[P_{2}=2\,P_{1}\]
\[P_{1}=\frac{W_{1}}{t_{1}}\] \[P_{2}=\frac{W_{2}}{t_{2}}\] \[P_{2}=2\,P_{1}\] \[\frac{W_{2}}{t_{2}}=2\,\frac{W_{1}}{t_{1}}\] \[\frac{W_{1}}{W_{2}}=\frac{t_{1}}{2\,t_{2}}\] Lako se vidi da je točan odgovor C.
4. zadatak
Međunarodna svemirska stanica kruži oko Zemlje na visini 400 km iznad površine.
Koja bi od navedenih tvrdnja bila točna za iznos gravitacijske sile koja djeluje na stanicu kada bi stanica
kružila na visini 800 km iznad površine Zemlje? Polumjer Zemlje iznosi 6370 km.
- A. Iznos gravitacijske sile ostao bi isti.
- B. Iznos gravitacijske sile smanjio bi se na četvrtinu početnoga iznosa.
- C. Iznos gravitacijske sile smanjio bi se na polovinu početnoga iznosa.
- D. Iznos gravitacijske sile smanjio bi se na više od polovine početnoga iznosa.
Gravitacijska sila kojom Zemlja djeluje na međunarodnu svemirsku stanicu, koja se nalazi na visini h iznad površine Zemlje: \[F=G\,\frac{m\,M_\textrm{Z}}{\left(R+h\right)^{2}}\] Polumjer Zemlje označen je sa R.
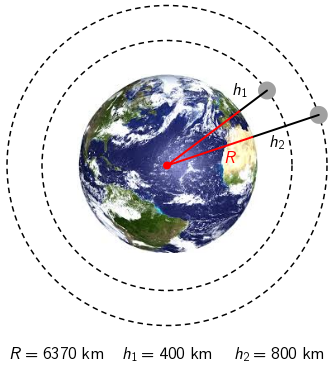
Kada se svemirska stanica nalazi na visini h1 iznad površine Zemlje, Zemlja na nju djeluje gravitacijskom silom: \[F_{1}=G\,\frac{m\,M_\textrm{Z}}{\left(R+h_{1}\right)^{2}}\] Na visini h2 ta će sila iznositi: \[F_{2}=G\,\frac{m\,M_\textrm{Z}}{\left(R+h_{2}\right)^{2}}\] Podijelimo drugu jednadžbu prvom: \[\frac{F_{2}}{F_{1}}=\frac{G\,\large\frac{m\,M_\textrm{Z}}{\left(R+h_{2}\right)^{2}}}{G\,\large\frac{m\,M_\textrm{Z}}{\left(R+h_{1}\right)^{2}}}=\frac{\left(R+h_{1}\right)^{2}}{\left(R+h_{2}\right)^{2}}\] \[F_{2}=\frac{\left(R+h_{1}\right)^{2}}{\left(R+h_{2}\right)^{2}}\,F_{1}\] \[F_{2}=\frac{6770^{2}}{7170^{2}}\,F_{1}\] \[F_{2}=0,89\,F_{1}\] Točan odgovor je D.
5. zadatak
Horizontalna cilindrična cijev na jednome je kraju dvostruko manjega promjera nego na drugome. Kroz cijev struji idealni fluid bez turbulencija.
Koliki je omjer brzine strujanja fluida kroz uži i brzine strujanja fluida kroz širi kraj te cijevi?
- A. 1/4
- B. 1/2
- C. 2
- D. 4
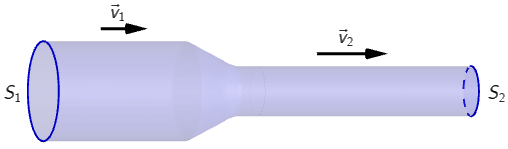
Primijenite jednadžbu kontinuiteta: \[S_{1}\,v_{1}=S_{2}\,v_{2}\]
Površina poprečnog presjeka cijevi: \[S=r^{2}\,\pi\] Polumjer cijevi dva puta je manji od njezinog promjera: \[r=\frac{d}{2}\] \[S=\frac{d^{2}}{4}\,\pi\] \[S_{1}=\frac{d_{1}^{\;2}}{4}\,\pi\] \[S_{2}=\frac{d_{2}^{\;2}}{4}\,\pi\] Iz jednadžbe kontinuiteta: \[S_{1}\,v_{1}=S_{2}\,v_{2}\] dobijemo: \[\frac{v_{2}}{v_{1}}=\frac{S_{1}}{S_{2}}\] \[\frac{v_{2}}{v_{1}}=\left(\frac{d_{1}}{d_{2}}\right)^{2}\] \[d_{1}=2\,d_{2}\] \[\frac{v_{2}}{v_{1}}=4\] Točan odgovor je D.
6. zadatak
Koja je od navedenih tvrdnja za produljenje metalne šipke pri zagrijavanju točna?
- A. Produljenje ovisi o promjeni temperature, vrsti metala i početnoj duljini šipke.
- B. Produljenje ovisi o promjeni temperature i početnoj duljini šipke, ali ne ovisi o vrsti metala.
- C. Produljenje ovisi o vrsti metala i početnoj duljini šipke, ali ne ovisi o promjeni temperature.
- D. Produljenje ovisi o vrsti metala i promjeni temperature, ali ne ovisi o početnoj duljini šipke.
U knjižici formula pronađite izraz za linearno toplinsko širenje metalne šipke, štapa ili žice.
Linearno toplinsko širenje metalne šipke prikažimo u obliku: \[\ell=\ell_{0}\left [1+\alpha\,\left ( t-t_{0} \right ) \right ]\]
- \(\ell\) - duljina šipke pri konačnoj temperaturi \(t\)
- \(\ell_{0}\) - duljina šipke pri početnoj temperaturi \(t_{0}\)
- \(\alpha\) - koeficijent linearnog toplinskog rastezanja; ovisi o vrsti metala
7. zadatak
Svaki od dvaju idealnih jednoatomnih plinova različitih masa atoma nalaze se u svojoj posudi. Posude su međusobno jednake i održavaju se na
stalnoj temperaturi 0 oC.
Koja od navedenih tvrdnja vrijedi za srednje kinetičke energije \(\overline{E}_\textrm{k}\) čestica tih idealnih plinova?
- A. \(\overline{E}_\textrm{k}\) čestica tih plinova su jednake i iznose 0 J.
- B. \(\overline{E}_\textrm{k}\) čestica tih plinova su jednake i veće od 0 J.
- C. \(\overline{E}_\textrm{k}\) čestica plina veće mase atoma veća je od \(\overline{E}_\textrm{k}\) čestica plina manje mase atoma.
- D. \(\overline{E}_\textrm{k}\) čestica plina veće mase atoma manja je od \(\overline{E}_\textrm{k}\) čestica plina manje mase atoma.
U knjižici formula pronađite izraz za srednju kinetičku energiju molekula jednoatomnog idealnog plina.
Napomena:
Molekule jednoatomnog idealnog plina sastoje se od jednog atoma.
Iz izraza za srednju kinetičku energiju molekula jednoatomnog idealnog plina
\[\overline{E}_{\textrm{k}}=\frac{3}{2}\,k\,T\]
vidimo da ta energija ne ovisi o masi molekula nego o apsolutnoj temperaturi, koja iznosi \(T=273,15\,\textrm{K}.\)
Prema tome, točan odgovor je B.
8. zadatak
Idealni jednoatomni plin nalazi se pri atmosferskome tlaku p u zatvorenoj posudi stalnoga volumena V.
Kad se plinu dovede neka količina topline, apsolutna temperatura poraste mu za 10 %.
Koliki je rad plin obavio tijekom dovođenja topline?
- A. -pV
- B. 0
- C. 0,1 pV
- D. pV
Prema prvom zakonu termodinamike, toplina dovedena sustavu pretvara se u mehanički rad i promjenu unutarnje energije tog sustava. \[Q=W+\Delta U\] Plin obavlja rad ako mu se volumen povećava. Ako okolina obavlja rad, volumen plina se smanjuje.
Plin se nalazi u zatvorenoj posudi (izohorni proces) pa mu se volumen ne može mijenjati. U izohornom procesu plin ne obavlja rad.
\[W= 0\]
Točan odgovor je B.
Toplina dovedena plinu pretvara se u njegovu unutarnju energiju.
9. zadatak
Korisnost Carnotova toplinskog stroja je 0,24, dok mu je topliji spremnik zagrijan na 400 oC.
Kolika je temperatura hladnijega spremnika?
- A. 96 oC
- B. 238 oC
- C. 304 oC
- D. 511 oC
Korisnost toplinskog stroja: \[\eta=1-\frac{|Q_{2}|}{Q_{1}}\] \(Q_{1}\) je toplina koju stroj prima od toplijeg spremnika, a \(Q_{2}\) toplina koju stroj predaje hladnijem spremniku. Za Carnotov stroj vrijedi: \[\frac{|Q_{2}|}{Q_{1}}=\frac{T_{2}}{T_{1}}\] Zbog toga se korisnost Carnotovog stroja može prikazati kao: \[\eta=1-\frac{T_{2}}{T_{1}}\]

Iz korisnosti Carnotovog stroja \[\eta=1-\frac{T_{2}}{T_{1}}\] odredimo temperaturu hladnijeg spremnika: \[T_{2}=T_{1}\cdot \left(1-\eta\right)\] \[T_{1}=400\,^{o}\textrm{C}=673,15\,\textrm{K}\] \[T_{2}=511,59\,\textrm{K}=238,44\,^{o}\textrm{C} \] Točan odgovor je B.
10. zadatak
Tri pozitivno nabijena točkasta naboja Q1 = 4 nC ,
Q2 = 1 nC i
Q3 = 9 nC smještena su na istome pravcu.
Naboji Q1 i
Q3 trajno su učvršćeni u prostoru, a naboj
Q2 nalazi se između njih.
Kad je udaljenost između Q1 i
Q2 jednaka a, a udaljenost između
Q2 i
Q3 jednaka b, ukupna sila na naboj
Q2 jednaka je nuli.
Koliki je omjer udaljenosti a/b?
- A. a/b = 4/9
- B. a/b = 2/3
- C. a/b = 9/4
- D. a/b = 3/2
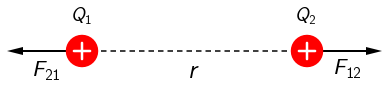
Sila kojom međusobno djeluju dva točkasta naboja prikazuje se Coulombovim zakonom: \[F=k\,\frac{Q_{1}\,Q_{2}}{r^{2}}\] Ako su naboji jednakog predznaka, sila je odbojna, a ako su suprotnog predznaka, sila je privlačna.
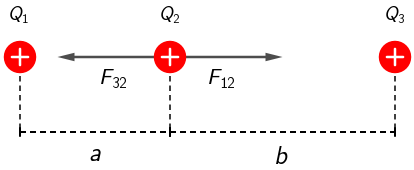
Naboj Q1 djeluje na naboj Q2 silom: \[F_{12}=k\,\frac{Q_{1}\,Q_{2}}{a^{2}}\] Naboj Q3 djeluje na naboj Q2 silom: \[F_{32}=k\,\frac{Q_{3}\,Q_{2}}{b^{2}}\] Te dvije sile moraju biti jednake: \[k\,\frac{Q_{1}\,Q_{2}}{a^{2}}=k\,\frac{Q_{3}\,Q_{2}}{b^{2}}\] \[\frac{Q_{1}}{a^{2}}=\frac{Q_{3}}{b^{2}}\] \[\frac{a}{b}=\sqrt{\frac{Q_{1}}{Q_{3}}}=\sqrt{\frac{4}{9}}\] \[\frac{a}{b}=\frac{2}{3}\] Točan odgovor je B.
11. zadatak
Kondenzator kapaciteta C1 spoji se na izvor određenoga napona
U tako da energija električnoga polja kondenzatora iznosi 0,5 nJ.
Kad se kondenzator kapaciteta C2 spoji na izvor jednakoga napona
U, energija njegova električnog polja iznosi 4,5 nJ.
Koliko iznosi omjer kapaciteta C2/C1
- A. \(\large{\frac{C_{2}}{C_{1}}}=\normalsize{\sqrt{3}}\)
- B. \(\large{\frac{C_{2}}{C_{1}}}=\normalsize{2,25}\)
- C. \(\large{\frac{C_{2}}{C_{1}}}=\normalsize{3}\)
- D. \(\large{\frac{C_{2}}{C_{1}}}=\normalsize{9}\)
Energija električnog polja kondenzatora: \[W=\frac{1}{2}\,C\,U^{2}\]
\begin{matrix} \begin{align*} &W_{1} = \frac{1}{2}\,C_{1}\,U^{2}\\ &W_{2} = \frac{1}{2}\,C_{2}\,U^{2} \end{align*} \end{matrix} Podijelimo drugu jednadžbu prvom: \begin{matrix} \begin{align*} &\frac{C_{2}}{C_{1}}=\frac{W_{2}}{W_{1}}\\ &\frac{C_{2}}{C_{1}}=\frac{4,5}{0,5}\\ &\frac{C_{2}}{C_{1}}=9 \end{align*} \end{matrix} Točan odgovor je D.
12. zadatak
Slika prikazuje strujni krug sa spojenom idealnom baterijom nepoznatoga napona.
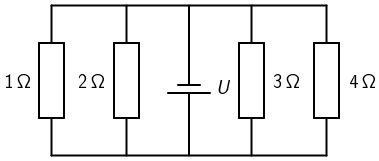
Kroz koji otpornik prolazi najviše naboja u jedinici vremena?
- A. kroz otpornik otpora 1 Ω
- B. kroz otpornik otpora 2 Ω
- C. kroz otpornik otpora 3 Ω
- D. kroz otpornik otpora 4 Ω
Napon (pad napona) na paralelno spojenim otporima je jednak.
Struju kroz pojedini otpor odredimo na osnovu Ohmovog zakona za dio strujnog kruga:
\[I=\frac{U}{R}\]
U zadatku se traži kroz koji otpornik prolazi najviše naboja u jedinici vremena, a to je struja:
\[I=\frac{\Delta Q}{\Delta t}\]
Napon na svim otporima jednak je naponu izvora struje \(U\).
Na osnovu Ohmovog zakona:
\[I=\frac{U}{R}\]
zaključujemo da će najveća struja prolaziti kroz otpornik najmanjeg otpora.
To je otpornik kojemu je otpor \(1\,\Omega.\)
Točan odgovor je A.
13. zadatak
Ravnim vodičem prolazi struja koja na udaljenosti r od vodiča stvara magnetsko polje iznosa B.
Koliki je iznos magnetskoga polja na udaljenosti 2r od vodiča?
- A. B/8
- B. B/4
- C. B/2
- D. B
Magnetsko polje u nekoj točki oko dugog ravnog vodiča, kojim prolazi struja, obrnuto je proporcionalno udaljenosti te točke od osi vodiča:
\[B\sim \frac{1}{r}\]
Ako se udaljenost točke poveća dva puta, magnetsko će se polje smanjiti 2 puta.
Točan odgovor je C.
14. zadatak
Slika prikazuje negativno nabijenu česticu koja ulijeće početnom brzinom v0 u prostor u kojemu se nalazi homogeno magnetsko polje \(\vec{B}.\) Čestica u polju opiše polukružnicu i zatim ga napusti.
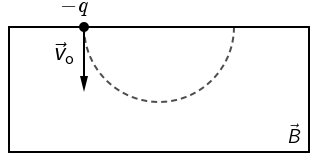
Koji je smjer magnetskog polja \(\vec{B}\) ?
- A. \(\bigotimes \)
- B. \(\bigodot\)
- C. \(\rightarrow\)
- D. \(\leftarrow\)
Smjer i orijentaciju sile koja djeluje na pozitivno nabijenu česticu koja se giba u magnetskom polju određujemo pravilom desne ruke.
Smjer i orijentaciju sile koja djeluje na negativno nabijenu česticu koja se giba u magnetskom polju određujemo pravilom lijeve ruke.
Palac lijeve ruke postavimo u smjer brzine, dlan postavimo tako da je okomica na dlan usmjerena prema središtu polukružnice
(sila kojom magnetsko polje djeluje na nabijenu česticu ima ulogu centripetalne sile), ispruženi prsti pokazuju smjer magnetskog polja.
Magnetsko polje je okomito na ravninu crtanja i usmjereno je iz ravnine crtanja.Točan odgovor je B.
15. zadatak
Graf prikazuje ovisnost elongacije o vremenu za harmonijsko titranje jedne čestice.
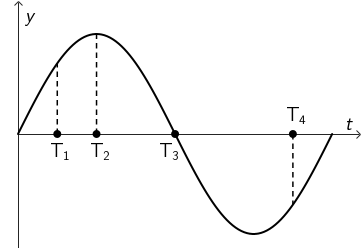
U kojoj točki označenoj na vremenskoj osi akceleracija čestice iznosi nula?
- A. u točki T1
- B. u točki T2
- C. u točki T3
- D. u točki T4
Čestica će harmonijski titrati ako na nju djeluje harmonijska sila: \[\vec{F}=-k\,\vec{y}\] Preznak minus znači da je orijentacija harmonijske sile suprotna orijentaciji elongacije.

Primijenimo temeljni zakon gibanja kako bismo odredili akceleraciju:
\[\vec{a}=\frac{\vec{F}}{m}\]
\[\vec{a}=\frac{-k\,\vec{y}}{m}\]
Iz prethodne jednadbe zaključujemo:
\[y=0\,\Rightarrow a=0\]
Ako je elongacija jednaka nuli, onda je i akceleracija jednaka nuli.
Od ponuđenih točaka na vremenskoj osi, samo u točki T3 elongacija je jednaka nuli.
Točan odgovor je C.
16. zadatak
Transverzalni val amplitude A i frekvencije f prostire se u
x, y ravnini duž napete niti u smjeru osi x brzinom v.
Koja od navedenih tvrdnja točno opisuje maksimalnu brzinu pojedine čestice niti?
- A. Maksimalna brzina čestice iznosi 2fA i usmjerena je duž osi x.
- B. Maksimalna brzina čestice iznosi 2fA i usmjerena je duž osi y.
- C. Maksimalna brzina čestice iznosi 2πfA i usmjerena je duž osi x.
- D. Maksimalna brzina čestice iznosi 2πfA i usmjerena je duž osi y.
Transverzalni val putuje sredstvom u obliku bregova i dolova. Čestice sredstva titraju oko ravnotežnog položaja okomito na smjer širenja vala.
Transverzalni val je progresivan val.
Ako je transverzalni val koji se širi napetim užetom harmonijski val, njegova je jednadžba:
\[y\left ( x,\,t \right )=A\,\textrm{sin}\left (\omega \,t - k\,x\right)\]
Veličine kojima opisujemo val:
- \(\omega=\Large{\frac{2\,\pi}{T}}\) - kutna frekvencija
- \(k=\Large{\frac{2\,\pi}{\lambda}}\) - valni broj
- \(A\) - amplituda
- \(T\) - period
- \(\lambda\) - valna duljina
Valna jednadžba omogućuje nam odrediti položaj čestice sredstva kroz kojega se širi val na bilo kojem mjestu i u bilo kojem trenutku:
\[y\left ( x,\,t \right )=A\,\textrm{sin}\left (\omega \,t - k\,x\right)\]
Brzinu titranja čestica harmonijskog vala odredimo kao derivaciju jednadžbe za elongaciju čestica u ovisnosti o vremenu:
\[v=\frac{dy}{dt}\]
\[v=A\,\omega\,\textrm{cos}\left(\omega\,t-k\,x \right)\]
Brzina čestica sredstva je najveća kada je:
\[\textrm{cos}\left(\omega\,t-k\,x \right)=1\]
jer je maksimalna vrijednost funkcije kosinus jednaka jedan. Prema tome, najveća brzina je:
\[v_{_{\large{0}}}=A\,\omega\]
Kutna frekvencija:
\[\omega=\frac{2\,\pi}{T}\]
Frekvencija titranja čestica:
\[f=\frac{1}{T}\]
Prema tome, kutnu frekvenciju prikazujemo i kao:
\[\omega=2\,\pi\,f\]
Najveća brzina:
\[v_{_{\large{0}}}=2\,\pi\,f\,A\]
Čestice sredstva titraju okomito na smjer osi x, pa je brzina usmjerena duž osi y.
Točan odgovor je D.
17. zadatak
Detektor na udaljenosti r od izvora zvuka snage P mjeri razinu zvuka L.
Što se događa sa snagom izvora i razinom zvuka udaljavanjem detektora od izvora?
- A. Snaga izvora i razina zvuka se mijenjaju.
- B. Snaga izvora i razina zvuka ostaju jednaki.
- C. Snaga se izvora ne mijenja, a razina se zvuka mijenja.
- D. Snaga se izvora mijenja, a razina se zvuka ne mijenja.
Snaga izvora zvuka, npr. zvučnika, jednaka je energiji koju izvor zvuka emitira u jedinici vremena: \[P=\frac{E}{t}\] Energija E zvučnog vala koja prolazi kroz jediničnu površinu u jedinici vremena okomito na smjer širenja energije zvučnog vala zove se jakost ili intenzitet zvuka: \[I=\frac{E}{S\,t}\] Točkasti izvor zvuka emitira zvuk jednako u svim smjerovima. Intenzitet zvuka u nekoj točki ovisi o udaljenosti r te točke od izvora zvuka. Intenzitet točkastog izvora zvuka u nekoj točki ovisi o udaljenosti te točke od izvora zvuka (obrnuto je proporcionalan kvadratu udaljenosti te točke od izvora zvuka): \[I=\frac{E}{4\pi\,r^2\,t}\] Osjet zvuka koji čujemo nije proporcionalan njegovoj jakosti (deset puta jači zvuk ne izaziva deset puta jači osjet). Odziv ljudskog uha takav je da je osjet zvuka približno proporcionalan logaritmu jakosti zvuka. Zato definirano razinu jakosti (intenziteta) zvuka, koju označujemo s L: \[L=10\,\textrm{log}\,\frac{I}{I_{0}}\] I0 je prag čujnosti (najmanja jakost zvuka koju ljudsko uho može čuti): \[I_{0}=10^{\mathbf{-}12}\,\textrm{W}/\textrm{m}^{2}\]
Snaga izvora zvuka određena je konstrukcijom izvora. Udaljavanjem detektora od izvora snaga izvora se ne mijenja.
Intenzitet zvuka koji dolazi do detektora mijenja se udaljavanjem detektora. (Ako se radi o točkastom izvoru zvuka, intenzitet je obrnuto proporcionalan kvadratu udaljenosti detektora od izvora.) Zbog toga će se mijenjati i razina intenziteta zvuka: \[L=10\,\textrm{log}\,\frac{I}{I_{0}}\] Točan odgovor je C.
18. zadatak
Slika prikazuje zraku svjetlosti pri prijelazu iz optičkoga sredstva A u optičko sredstvo B.
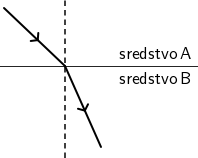
Što je točno za brzinu i valnu duljinu svjetlosti pri prijelazu iz optičkoga sredstva A u optičko sredstvo B?
- A. Brzina i valna duljina se smanjuju.
- B. Brzina i valna duljina se povećavaju.
- C. Brzina se smanjuje, a valna se duljina povećava.
- D. Brzina se smanjuje, a valna se duljina ne mijenja.
Kada svjetlost prelazi iz jednog sredstva u drugo, mijenja joj se brzina, prema tome i valna duljina, dok frekvencija ostaje ista.
Pritom na granici sredstava dolazi do loma zrake svjetlosti. Ako je brzina svjetlosti u sredstvu iz kojega upada na granicu veća od
brzine u sredstvu u koje upada, zraka svjetlosti lomi se prema okomici. U suprotnom lomila bi se od okomice.
Brzina svjetlosti u sredstvu A: \[v_{\small{\textrm{A}}}=f\,\lambda_{\small{\textrm{A}}}\] Brzina svjetlosti u sredstvu B: \[v_{\small{\textrm{B}}}=f\,\lambda_{\small{\textrm{B}}}\] Podijelimo drugu jednadžbu prvom: \[\frac{v_{\small{\textrm{B}}}}{v_{\small{\textrm{A}}}}=\frac{\lambda_{\small{\textrm{B}}}}{\lambda_{\small{\textrm{A}}}}\qquad (1)\] Zraka svjetlosti lomi se prema okomici pa je brzina svjetlosti u sredstvu B manja nego u sredstvu A: \[v_{\small{\textrm{B}}} < v_{\small{\textrm{A}}}\Rightarrow \frac{v_{\small{\textrm{B}}}}{v_{\small{\textrm{A}}}} < 1\] Iz jednadžbe (1) zaključujemo da je: \[\frac{\lambda_{\small{\textrm{B}}}}{\lambda_{\small{\textrm{A}}}} < 1\] Točan odgovor je A.
19. zadatak
Graf prikazuje ovisnost intenziteta elektromagnetskoga zračenja daleke zvijezde o valnoj duljini.
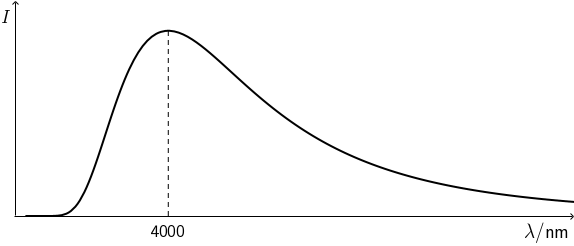
Kojemu dijelu elektromagnetskoga spektra pripada zračenje najvećega intenziteta?
- A. UV zračenju
- B. vidljivomu zračenju
- C. infracrvenomu zračenju
- D. radio valovima
Pomoć potražite na poveznici Elektromagnetski spektar
Iz grafa vidimo da je najveći intenzitet zračenja na valnoj duljini 4000 nm. Ova valna duljina je desetak puta veća od valne
duljine crvene svjetlosti. Frekvencija zračenja obrnuto je proporcionalna valnoj duljini:
\[f=\frac{c}{\lambda}\]
Prema tome, frekvencija je manja od frekvencije crvene svjetlosti pa se radi o infracrvenom zračenju.
Točan odgovor je C.
20. zadatak
Valna je duljina plave svjetlosti granična valna duljina za fotoelektrični učinak za neku metalnu pločicu.
Kojim laserom treba obasjati istu pločicu kako bi došlo do fotoelektričnoga učinka?
- A. laserom koji emitira infracrveno zračenje
- B. laserom koji emitira crvenu svjetlost
- C. laserom koji emitira zelenu svjetlost
- D. laserom koji emitira ljubičastu svjetlost
Graf kinetičke energije fotoelektrona u ovisnosti o frekvanciji:
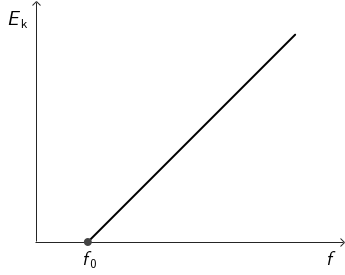
Fotoefekt se počinje opažati ako je energija fotona elektromagnetskog zračenja, koje upada na metal, jednaka izlaznom radu W 0 , koji je potrebno obaviti kako bi došlo do fotoefekta: \begin{matrix} \begin{align*} &E_{f}=W_{0}\\ &E_{f}=h\,f_{0}\\ \end{align*} \end{matrix} Energija zračenja koje pada na metal može izbaciti elektrone iz metala, ali i ne mora. To ovisi o frekvenciji upadnog zračenja. Za svaki metal postoji neka granična frekvencija, koju označujemo s f0 . Ako na metal pada zračenje manje frekvencije, fotoelektričnog učinka nema, bez obzira koliki bio intenzitet upadnog zračenja. Ako je frekvencija upravo jednaka graničnoj, fotoelektrični učinak se počinje opažati. Ako je frekvencija veća od granične, dolazi do emisije fotoelektrona, ma koliko bio mali intenzitet upadnog zračenja. Pri tome je kinetička energija linearna funkcija frekvencije.
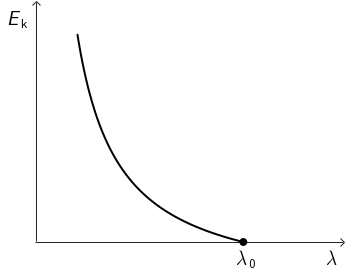
Iz grafa koji prikazuje kinetičku energije fotoelektrona u ovisnosti o valnoj duljini zaključujemo:
- Ako je \(\lambda < \lambda_{0}\) - fotoefekt, kinetička energija fotoelektrona obrnuto je proporcionalna valnoj duljini upadne svjetlosti. \[E_{k}=\frac{h\,c}{\lambda}\]
- Ako je \(\lambda = \lambda_{0}\) - fotoefekt se još opaža
- Ako je \(\lambda > \lambda_{0}\) - fotoefekt se ne opaža.
Točan odgovor je D.
21. zadatak
Koja od navedenih pojava ukazuje na valnu prirodu elektrona?
- A. fotoelektrični učinak
- B. ogib elektrona prolaskom kroz pukotinu
- C. usmjereno gibanje elektrona u vodičima
- D. ubrzavanje elektrona između ploča kondenzatora
Interferencija i ogib su pojave koje opažamo kod bilo kojih valova. Ako elektron ima valna svojstva, morali bismo primijetiti te pojave i kod elektrona.
Točan odgovor je B.
Shema eksperimentalnog uređaja pomoću kojega demonstriramo ogib svjetlosti ili elektrona.
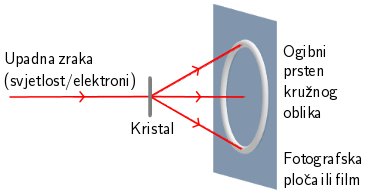
Valna duljina rendgenskih zraka iznosi između 0,01 nm i 10 nm. Da bismo mogli opaziti ogib rendgenskih zraka potrebna je pukotina koja nije puno veća od valne duljine rendgenskih zraka.
De Broglieva valna duljina elektrona koji se giba brzinom 106 m/s iznosi: \[\lambda=\frac{h}{mv}=\frac{6,626\cdot 10^{\large{-}\normalsize{34}}}{9,11\cdot 10^{\large{-}\normalsize{31}}\cdot 10^6}=0,73\,\textrm{nm}\]
Fizičari su na početku 20. stoljeća željeli odrediti valnu duljinu rendgenskih zraka pomoću ogiba na optičkoj rešetki. Rezultati nisu bili uspješni jer je teško napraviti rešetku s dovoljno uskim pukotinama. Njemački fizičar Max von Laue dosjetio se da takve rešetke nije potrebno praviti jer one već postoje. Kao "optičku rešetku" koristio je sloj pravilno poredanih atoma u kristalu. Udaljenost između atoma u kristalima po redu je veličine \(10^{-10}\,\textrm{m}\).
Rendgenske zrake, koje su elektromagnetski valovi, usmjerimo na kristal. Na atomima kristala dolazi do ogiba.

Ogibna slika rendgenskih zraka na fotografskoj ploči
Usmjerimo li snop elektrona, kojima je de Broglieva valna duljina jednaka valnoj duljini rendgenskih zraka, na fotografskoj ploči također ćemo dobiti ogibni uzorak.
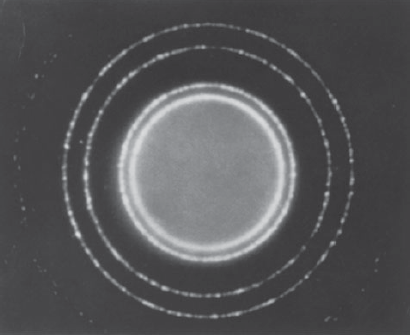
Ogibna slika elektrona na fotografskoj ploči
Ovo je eksperimentalni dokaz valnih svojstava elektrona.
22. zadatak
Na slici je prikazan dio energijskih razina za neki atom.
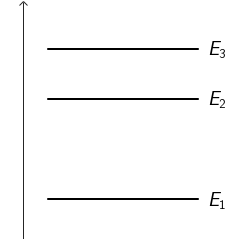
Razmak između razina E1 i
E2 dva je puta veći od razmaka između razina
E2 i
E3. Kad elektron prijeđe s razine
E3 na razinu
E2, emitira foton valne duljine λ.
Koje još valne duljine može imati foton koji se emitira pri prijelazu elektrona iz viših u niža energijska stanja?
- A. samo λ/2
- B. λ/2 i λ/3
- C. samo 2 λ
- D. 2 λ i 3 λ
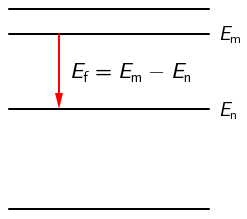
Pri prijelazu elektrona s energijske razine Em na energijsku razinu En dolazi do emisije fotona energije: \[E_\textrm{f}=E_\textrm{m}-E_\textrm{n}\] Energiju fotona možemo prikazati i pomoću valne duljine fotona: \[E_\textrm{f}=\frac{h\,c}{\lambda_\textrm{m,n}}\Rightarrow \lambda_\textrm{m,n}=\frac{h\,c}{E_\textrm{f}}\] \[\lambda_\textrm{m,n}=\frac{h\,c}{E_\textrm{m}-E_\textrm{n}}\]
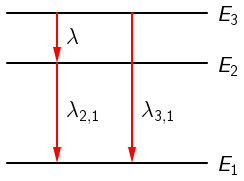
Valna duljina fotona koji nastaje prijelazom iz E3 u E2: \[\lambda=\frac{h\,c}{E_\textrm{3}-E_\textrm{2}}\qquad (1)\] Valna duljina fotona koji nastaje prijelazom iz E2 u E1: \[\lambda_{2,1}=\frac{h\,c}{E_\textrm{2}-E_\textrm{1}}\qquad(2)\] Prema zadatku vrijedi: \[E_\textrm{2}-E_\textrm{1}=2\,\left(E_\textrm{3}-E_\textrm{2}\right)\] Usporedbom jednadžbi (2) i (1) zaključujemo: \[\lambda_{2,1}=\frac{\lambda}{2}\] Valna duljina fotona koji nastaje prijelazom iz E3 u E1: \[\lambda_{3,1}=\frac{h\,c}{E_\textrm{3}-E_\textrm{1}}\qquad(3)\] Iz zadatka i slike vidimo da vrijedi: \[E_\textrm{3}-E_\textrm{1}=3\,\left(E_\textrm{3}-E_\textrm{2}\right)\] Usporedbom jednadžbi (3) i (1) zaključujemo: \[\lambda_{3,1}=\frac{\lambda}{3}\] Točan odgovor je B.
23. zadatak
Koji je od navedenih nuklearnih procesa fisija?
- A. raspad teške jezgre
- B. spajanje lakih jezgara
- C. spajanje teških jezgara
- D. gama-raspad lake jezgre
Fisija je nuklearna reakcija pri kojoj projektil razdijeli jezgru na dva podjednaka dijela uz oslobađanje nekoliko neutrona. Ti neutroni mogu pogoditi druge jezgre i tako izazvati nove fisije. U svakoj se fisiji oslobađa energija. Jezgre s velikim brojem protona su pogodne za fisiju. Električna sila između protona je zbog male udaljenosti između njih ogromna, no jezgra se ipak ne razleti jer ju na okupu drži jaka sila koja djeluje između nukleona. Takve su jezgre spremne za raspad, ali potrebno je malo povećati razmak između protona kako bi jaka sila, koja ih drži na okupu oslabila. To se u procesu fisije postiže gađanjem jezgre neutronima.
Masa bilo koje stabilne jezgre manja je od ukupne mase slobodnih nukleona koji čine tu jezgru. Zato se izgradnjom takvih jezgara oslobađa energija.
Fuzija je nuklearna reakcija u kojoj od slobodnih nukleona nastaje jezgra ili proces u kojemu se lake jezgre spajaju u teže jezgre
uz oslobađanje energije. Energija koja se stvara u Suncu jest energija oslobođena u procesima fuzije.
Točan odgovor je A.
24. zadatak
Slika prikazuje dio torijeva niza prirodnih radionuklida koji završava stabilnim olovom.
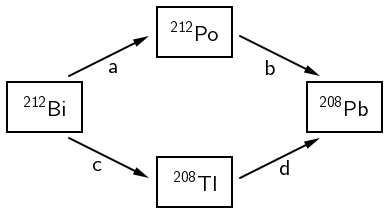
- A. a i c su β− čestice, b i d su α čestice
- B. a i d su β− čestice, b i c su α čestice
- C. a i d su γ čestice, b i c su β− čestice
- D. a i c su α čestice, b i d su β− čestice
Jezgru atoma simbolički označavamo kao: \[{_\textrm{Z}^\textrm{A}}\textrm{X}\] X je simbol kemijskog elementa kojemu jezgra pripada.
Broj protona u jezgri, Z , zovemo atomskim ili protonskim brojem.
Atomski broj jednak je rednom broju atoma u periodnom sustavu.
Ukupan broj nukleona u jezgri, A , zovemo masenim ili nukleonskim brojem.
Broj neutrona u jezgri jednak je:
N = A - Z
Beta-minus raspad
\[{_\textrm{Z}^\textrm{A}}\,\textrm{X}\rightarrow {_{\textrm{Z}\texttt{+}1}^{\,\,\,\,\textrm{A}}}\,\textrm{Y}+{_{\texttt{-}1}^{\,\,0}}\,\textrm{e}+\overline{\nu}\]
Beta-plus raspad
\[{_\textrm{Z}^\textrm{A}}\,\textrm{X}\rightarrow {_{\textrm{Z}\texttt{-}1}^{\,\,\,\,\textrm{A}}}\,\textrm{Y}+{_{\texttt{+}1}^{\,\,0}}\,\textrm{e}+\nu\]
Alfa raspad
\[{_\textrm{Z}^\textrm{A}}\,\textrm{X}\rightarrow {_{\textrm{Z}\texttt{-}2}^{\textrm{A-4}}}\,\textrm{Y}+{_{2}^{4}}\,\textrm{He}\]
Beta-raspadom neke jezgre X nastaje nova jezgra Y kojoj je maseni broj jednak masenom broju jezgre X.
Alfa-raspadom neke jezgre X nastaje nova jezgra Y kojoj je maseni broj za četiri manji od masenog broja jezgre X.
Na osnovu slike u zadatku zaključujemo:
- a i d su beta-minus raspadi
- b i c su alfa-raspadi
25. zadatak
Volumen idealnoga plina prilikom izobarne ekspanzije povećao se za 2,5·10-3 m3
pri tlaku 2·106 Pa.
Koliko iznosi rad koji je obavio idealni plin pri ekspanziji?
Odgovor:
Rad plina pri stalnom tlaku: \[W=p\,\Delta V\]
\[W=p\,\Delta V\] \[W=2\cdot 10^{6}\cdot 2,5\cdot 10^{-3}=5000\,\textrm{J}\]
26. zadatak
Otpornik otpora 3 Ω spojen je serijski sa zavojnicom i kondenzatorom na izvor izmjeničnoga napona tako da induktivni otpor
zavojnice iznosi 60 Ω, a kapacitivni otpor kondenzatora 100 Ω.
Koliko iznosi ukupni otpor toga RLC kruga?
Odgovor: \(\Omega\)
27. zadatak
Na vertikalno postavljenu oprugu ravnotežne duljine 20 cm i zanemarive mase ispusti se tijelo
mase 0,15 kg s visine 30 cm u odnosu na podlogu na kojoj se nalazi opruga. Pri padu tijelo
maksimalno sabije oprugu do duljine 12,5 cm.
Koliko iznosi konstanta elastičnosti opruge?
Odgovor:
Primijenite zakon očuvanja mehaničke energije.
Mehanička energija u početnom položaju jednaka je gravitacijskoj potencijalnoj energiji: \[E_{1}=E_\textrm{gp}\] \[E_{1}=m\,g\,h\] Pokrenite video. Mehanička energija u konačnom položaju jednaka je zbroju gravitacijske i elastične potencijalne energije: \[E_{2}=m\,g\,\ell+\frac{1}{2}\,k\,x^{2}\] Opruga se stisnula za: \[x=\ell_{0}-\ell\] \[E_{2}=m\,g\,\ell+\frac{1}{2}\,k\,\left(\ell_{0}-\ell\right)^{2}\] Zakon očuvanja mehaničke energije: \[E_{2}=E_{1}\] \[m\,g\,h=m\,g\,\ell+\frac{1}{2}\,k\,\left(\ell_{0}-\ell\right)^{2}\] \[k=\frac{2\,m\,g\,\left(h-\ell\right)}{\left(\ell_{0}-\ell\right)^{2}}=93,33\,\textrm{N/m}\]
28. zadatak
U menzuri površine presjeka 12 cm2 nalazi se ulje gustoće
900 kg/m3. Na površini ulja smješten je klip mase 0,1 kg koji točno prekriva
cijelu površinu ulja. Ukupni tlak na dnu menzure iznosi 104,5 kPa.
Koliko je visok stupac ulja u menzuri pri normiranome atmosferskom tlaku?
Odgovor:
Vanjski tlak koji djeluje na fluid u ravnoteži prenosi se jednako u sve njegove dijelove, a također i na stijenke posude u kojoj se nalazi i na tijela koja su u njega uronjena. Vanjski tlak nazivamo i hidraulički tlak. Ovo svojstvo fluida opisano je Pascalovim zakonom. Ako na fluid u ravnoteži djeluje vanjski tlak, tlak u svakoj točki fluida povećat će se za taj iznos.
Pretpostavimo da na neku tekućinu djeluje vanjski tlak \(p_{\textrm{v}}\).
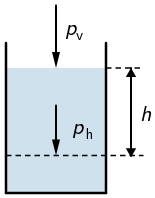
Ukupni tlak na dubini h u tekućini bit će jednak zbroju vanjskog i hidrostatskog tlaka na toj dubini: \[p=p_{\textrm{v}}+\rho\,g\,h\]
Vanjski tlak na površinu ulja jednak je zbroju atmosferskog tlaka \(p_\textrm{a}\) i tlaka zbog težine klipa \(p_\textrm{k}\):
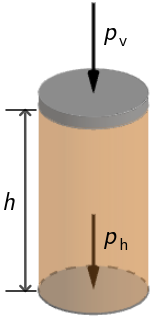
29. zadatak
U bakrenome kalorimetru mase 200 g nalazi se 300 g vode temperature
20 oC. U kalorimetar s vodom dovede se vodena para temperature
100 oC.
Koliku je masu vodene pare potrebno dovesti u kalorimetar da se pri temperaturi 42 oC uspostavi
termodinamička ravnoteža kalorimetra i vode nakon kondenzacije vodene pare?
Specifični toplinski kapacitet bakra iznosi 380 J/(kg K) , specifični toplinski kapacitet vode iznosi
4190 J/(kg K) , a specifična toplina isparavanja vode iznosi 2,26·106 J/kg.
Zanemarite gubitak topline u okolinu.
Odgovor:
Toplina potrebna za zagrijavanje tijela: \[Q=m\,c\,\Delta t\]
- \(m\)-masa tijela
- \(c\)-specifični toplinski kapacitet tijela
- \(\Delta t\)-porast temperature tijela \[\Delta t=t_\textrm{kon}-t_\textrm{poc}\]
- \(r\)-specifična toplina isparavanja
Početna temperatura bakrenog kalorimetra jednaka je temperaturi vode: \[t_\textrm{v}= 20\,^{\textrm{o}}\textrm{C}\] Dovođenjem vodene pare temperature: \[t_\textrm{p}= 100\,^{\textrm{o}}\textrm{C}\] treba doći do toplinske ravnoteže kalorimetra i vode (nakon kondenzacije vodene pare) pri temperaturi: \[t= 42\,^{\textrm{o}}\textrm{C}\] \[m_\textrm{b}\,c_\textrm{b}\left(t-t_\textrm{v}\right)+m_\textrm{v}\,c_\textrm{v}\left(t-t_\textrm{v}\right)=r\,m_\textrm{p}+m_\textrm{p}\,c_\textrm{v}\left(t_\textrm{p}-t\right)\] \[\left(m_\textrm{b}\,c_\textrm{b}+m_\textrm{v}\,c_\textrm{v}\right)\left(t-t_\textrm{v}\right)=m_\textrm{p}\left[ r+c_\textrm{v}\left(t_\textrm{p}-t\right)\right]\] \[m_\textrm{p}=\frac{\left(m_\textrm{b}\,c_\textrm{b}+m_\textrm{v}\,c_\textrm{v}\right)\left(t-t_\textrm{v}\right)}{r+c_\textrm{v}\left(t_\textrm{p}-t\right)}\] \[m_\textrm{p}=\frac{29326}{2503020}=0,011716\,\textrm{kg}\] \[m_\textrm{p}=11,72\,\textrm{g}\]
30. zadatak
Crvena svjetlost valne duljine 650 nm prolazi okomito kroz Youngove pukotine. Na slici su prikazani interferencijski maksimumi na milimetarskome papiru koji je paralelan s ravninom pukotina i od njih udaljen 110 cm.
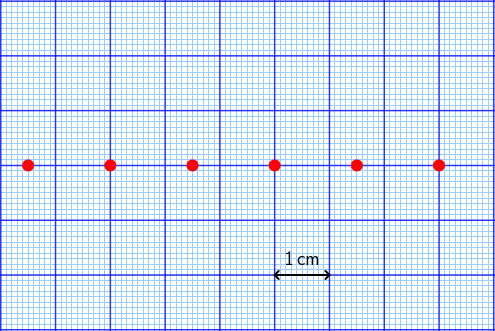
1. Kolika je udaljenost između susjednih maksimuma?
Odgovor:
Točke na milimetarskom papiru označuju položaje maksimuma.
s=1,5 cm.
2. Koliki je razmak između pukotina?
Odgovor:
Valna duljina svjetlosti kod Youngovog pokusa: \[\lambda=\frac{s\,d}{a}\]
- s - udaljenost između interferencijskih maksimuma
- d - razmak između pukotina
- a - udaljenost zastora od pukotina
Raznak između pukotina: \[d=\frac{\lambda\,a}{s}=4,77\cdot 10^{-5}\, \textrm{m}\]
31. zadatak
Tijelo mase 3 kg povlači se stalnom brzinom uz kosinu kuta nagiba 30o
uz pomoć vanjske sile koja je paralelna s kosinom. Koeficijent trenja između kosine i tijela jednak je 0,1.
Koliko iznosi rad vanjske sile na putu 10 cm?
Odgovor:
Odredite sve sile koje djeluju na tijelo. Primijenite Newtonov drugi ili prvi zakon. Tijelo se giba jednoliko pa je rezultanta svih sila koje na njega djeluju jednaka nuli.
Odredimo sile koje djeluju na tijelo:
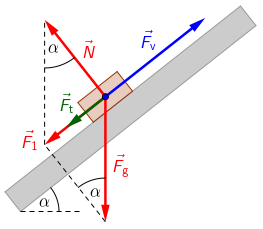
Na tijelo djeluju sljedeće sile:
- Sila teža - Fg
- Reakcija podloge - N
- Sila trenja - Ft
- Vanjska sila (vučna sila) - Fv
Reakcija podloge
\begin{matrix} \begin{align*} &N=F_\textrm{g}\,\textrm{cos}\,\alpha\\ &N=m\,g\,\textrm{cos}\,\alpha \end{align*} \end{matrix}Sila trenja
\begin{matrix} \begin{align*} &F_\textrm{t}=\mu\,N\\ &F_\textrm{t}=\mu\,m\,g\,\textrm{cos}\,\alpha \end{align*} \end{matrix}Rezultanta sila \(N\) i \(F_\textrm{g}\)
\begin{matrix} \begin{align*} &F_{1}=F_\textrm{g}\,\textrm{sin}\,\alpha\\ &F_{1}=m\,g\,\textrm{sin}\,\alpha \end{align*} \end{matrix}Rezultanta svih sila koje vuku tijelo prema dnu kosine
\begin{matrix} \begin{align*} &F_{1,\textrm{t}}=F_{1}+F_\textrm{t}\\ &F_{1,\textrm{t}}=m\,g\,\textrm{sin}\,\alpha+\mu\,m\,g\,\textrm{cos}\,\alpha \end{align*} \end{matrix}Vanjska sila \(F_\textrm{v}\) po iznosu mora biti jednaka sili \(F_{1,\textrm{t}}\)
\begin{matrix} \begin{align*} &F_\textrm{v}=F_{1,\textrm{t}}\\ &F_\textrm{v}=m\,g\,\textrm{sin}\,\alpha+\mu\,m\,g\,\textrm{cos}\,\alpha \end{align*} \end{matrix}Rad vanjske sile na putu s
\begin{matrix} \begin{align*} &W=F_\textrm{v}\cdot s\\ &W=\left(m\,g\,\textrm{sin}\,\alpha+\mu\,m\,g\,\textrm{cos}\,\alpha\right)\cdot s\\ &W=m\,g\,s\,\left(\textrm{sin}\,\alpha+\mu\,\textrm{cos}\,\alpha\right)\\ &W=1,76\,\textrm{J} \end{align*} \end{matrix}32. zadatak
Na slici je prikazan dio strujnoga kruga s otporima Rx i Ry jednakih iznosa.
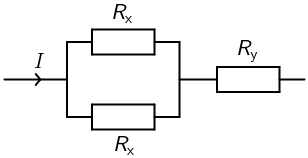
Otpornik otpora Rx = 200 Ω razvije toplinu
1,5 kJ u vremenu 10 sekundi.
Koji broj elektrona prođe otpornikom otpora Ry u istome vremenu?
Odgovor:
Rad električne struje \(W=U\,I\,t\) pretvara se u toplinu koja se oslobađa na otpornicima.
Primijenite prvo Kirchhoffovo pravilo u točkama grananja.
Struja je definirana kao naboj koji u jediničnom vremenu prođe poprečnim presjekom vodiča:
\[I=\frac{\Delta q}{\Delta t}\]
Taj naboj možemo prikazati pomoću broja elektrona:
\[\Delta q=N\,e\]
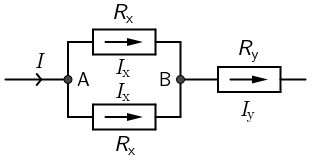
Napon na paralelno spojenim otporima Rx je jednak. Zbog toga će se struja
u točki A granati na dvije jednake struje Ix koje prolaze paralelno
spojenim otpornicima.
U točki B primijenimo prvo Kirchhoffovo pravilo:
\[I_\textrm{x}+I_\textrm{x}=I_\textrm{y}\]
\[I_\textrm{y}=2\,I_\textrm{x}\]
Struju Ix odredimo pomoću topline koja se u njemu razvija:
\begin{matrix}
\begin{align*}
&W=U\,I_\textrm{x}\,t\\
&U=I_\textrm{x}\,R_\textrm{x}\\
&W={I_\textrm{x}}^{2}\,R_\textrm{x}\,t\\
&I_\textrm{x}=\sqrt{\frac{W}{R_\textrm{x}\,t}}\\
&I_\textrm{y}=2\,I_\textrm{x}\\
&I_\textrm{y}=2\,\sqrt{\frac{W}{R_\textrm{x}\,t}}\\
&I_\textrm{y}=\frac{N\,e}{t}\\
&N=\frac{I_\textrm{y}\,t}{e}\\
&N=2\,\sqrt{\frac{W}{R_\textrm{x}\,t}}\cdot \frac{t}{e}\\
&N=1,08\cdot 10^{20}
\end{align*}
\end{matrix}
33. zadatak
Zavojnica s 50 namotaja poprečnoga presjeka 0,15 m2 postavljena je u homogenome magnetskom polju tako da joj je poprečni presjek okomit na silnice polja. Iznos magnetskoga polja mijenja se u vremenu kao što je prikazano na slici. Smjer magnetskoga polja ne mijenja se u vremenu. Zavojnica ima otpor 0,5 Ω.
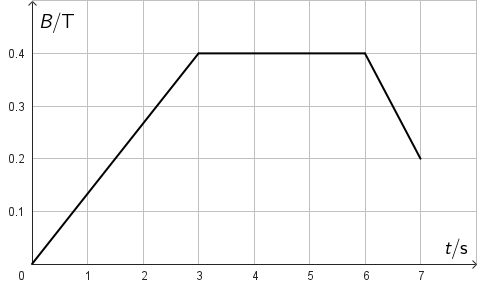
1. Koliko iznosi inducirani elektromotorni napon od šeste do sedme sekunde?
Odgovor:
Primijenimo Faradayev zakon: \[U_\textrm{i}=-N\frac{\Delta \Phi}{\Delta t}\] Promjenu magnetskog toka: \[\Phi=B\,S\] moguće je ostvariti promjenom magnetskog polja: \[\Delta \Phi=S\,\Delta B\] ili promjenom površine kroz koju prolaze magnetske silnice: \[\Delta \Phi=B\,\Delta S\]
Promjenu magnetskog toka očitamo iz grafa i primjenimo Faradayev zakon: \begin{matrix} \begin{align*} &U_\textrm{i}=-N\frac{\Delta \Phi}{\Delta t}\\ &U_\textrm{i}=-N\frac{S\,\Delta B}{\Delta t}\\ &U_\textrm{i}=-50\,\frac{0,15\,\left(0,2-0,4 \right)}{1}\\ &U_\textrm{i}=1,5\,\textrm{V} \end{align*} \end{matrix}
2. Koliko iznosi inducirana struja od šeste do sedme sekunde?
Odgovor:
Primijenimo Ohmov zakon: \[I_\textrm{i}=\frac{U_\textrm{i}}{R}\]
Na osnovu ohmovog zakona odredimo induciranu struju: \[I_\textrm{i}=\frac{U_\textrm{i}}{R}\] \[I_\textrm{i}=\frac{1,5}{0,5}\] \[I_\textrm{i}=3\,\textrm{A}\]
34. zadatak
Tijelo harmonijski titra amplitudom 5 cm. Period titranja tijela iznosi 0,1 s.
Koliko iznosi elongacija kada je brzina tijela 2 m/s?
Odgovor:
Jednadžba elongacije harmonijskog titranja: \[x=A\,\textrm{sin}\left(\omega\,t\right)\] Jednadžba brzine: \[v=\omega\,A\,\textrm{cos}\left(\omega\,t\right)\]
Iz jednadžbi za elongaciju i brzinu odredimo elongaciju za zadanu brzinu: \begin{matrix} \begin{align*} &x=A\,\textrm{sin}\left(\omega\,t\right)\\ &v=\omega\,A\,\textrm{cos}\left(\omega\,t\right)\\ &x^{2}=A^{2}\,\textrm{sin}^{2}\left(\omega\,t\right)\\ &v^{2}=\omega^{2}\,A^{2}\,\textrm{cos}^{2}\left(\omega\,t\right)\\ &\frac{x^{2}}{A^{2}}=\textrm{sin}^{2}\left(\omega\,t\right)\\ &\frac{v^{2}}{\omega^{2}\,A^{2}}=\textrm{cos}^{2}\left(\omega\,t\right)\\ &\frac{x^{2}}{A^{2}}+\frac{v^{2}}{\omega^{2}\,A^{2}}=\textrm{sin}^{2}\left(\omega\,t\right)+\textrm{cos}^{2}\left(\omega\,t\right)\\ &\frac{x^{2}}{A^{2}}+\frac{v^{2}}{\omega^{2}\,A^{2}}=1\\ &x^{2}+\frac{v^{2}}{\omega^{2}}=A^{2}\\ &x^{2}=A^{2}-\frac{v^{2}}{\omega^{2}}\\ &x=\sqrt{A^{2}-\frac{v^{2}}{\omega^{2}}}\\ &A=0,05\,\textrm{m};\;\omega=\frac{2\,\pi}{T}=20\,\pi;\,v=2\,\textrm{m/s}\\ &x=\sqrt{0,05^{2}-\frac{2^{2}}{\left(20\,\pi\right)^{2}}}\\ &x=0,038559\,\textrm{m}=3,86\,\textrm{cm} \end{align*} \end{matrix}
35. zadatak
Na slici je prikazana pravokutna kosina vlastite duljine hipotenuze 2 m i vlastita kuta
α = 45o koja se nalazi u svemirskome brodu koji se giba brzinom
0,866 c paralelno s bazom kosine.
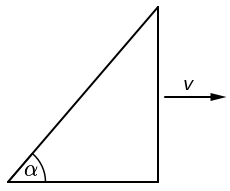
1. Koliku duljinu hipotenuze kosine mjeri mirni promatrač sa Zemlje?
Odgovor:
Dužine koje su okomite na smjer brzine ne mijenjaju se. Dužine u smjeru gibanja skraćuju se (kontrakcija duljine): \[L=L_{0}\,\sqrt{1-v^2/c^2}\] Skratit će se i komponenta hipotenuze u smjeru brzinu, dok će okomita komponenta ostati jednaka.
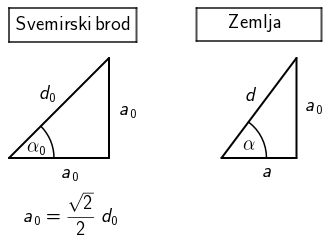
\begin{matrix} \begin{align*} &d_{0}=2\,\textrm{m}\\ &a_{0}=\frac{\sqrt{2}}{2}\cdot 2\\ &a_{0}=\sqrt{2}\,\textrm{m}\\ &v=0,866\cdot c\\ &a=a_{0}\,\sqrt{1-v^2/c^2}\\ &a=0,7072\,\textrm{m}\\ &d^{2}=a^{2}+{a_{0}}^{2}\\ &d=1,58\,\textrm{m} \end{align*} \end{matrix}
2. Koliki kut kosine mjeri mirni promatrač sa Zemlje?
Odgovor: \(\,^{\Large\textrm{o}}\)
Nakon što odredimo duljinu katete u smjeru gibanja, kut kosine odredimo pomoću trigonometrije.
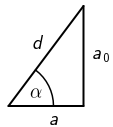
Iz trokuta na slici dobijemo: \begin{matrix} \begin{align*} &\textrm{tg}\,\alpha=\frac{a_{0}}{a}\\ &\alpha=63,43\,^{\Large\textrm{o}} \end{align*} \end{matrix}