Ogledni ispit za maturu 2022. godine
1. zadatak
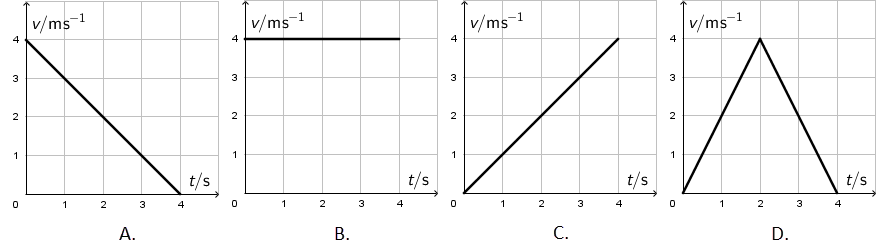
Na slici je prikazana ovisnost brzine o vremenu za četiri tijela.
Koje je tijelo prešlo najveći put?
- A. Tijelo A.
- B. Tijelo B.
- C. Tijelo C.
- D. Tijelo D.
Iz \(v,t\) grafa put određujemo kao površinu ispod grafa.
Tijelo B prešlo je put od \(4\cdot 4=16\,\textrm{m}\). Ostala tri tijela prešla su put od 8 m.
2. zadatak
Po horizontalnoj površini biljarskoga stola gibaju se jedna prema drugoj dvije kugle jednakih
masa \(m\) jednakim iznosima brzina \(v\). Kugle se centralno elastično sudare i odbiju jedna od
druge.
Koja je od navedenih tvrdnja ispravna? Zanemarite trenje između kugala i podloge.
- A. Ukupna količina gibanja kugala nakon sudara jednaka je nuli.
- B. Ukupna količina gibanja kugala nakon sudara jednaka je \(2mv\).
- C. Ukupna energija kugala nakon sudara jednaka je nuli.
- D. Ukupna energija kugala nakon sudara jednaka je \(2mv^{2}\).
Primijenite zakon očuvanja količine gibanja.
Pokrenite simulaciju.
Za elastičan sudar vrijede zakoni očuvanja količine gibanja i mehaničke energije, dok pri neelastičnom sudaru vrijedi samo zakon očuvanja količine
gibanja.
Prema zakonu očuvanja energije, kinetička energija prije sudara jednaka je kinetičkoj energiji nakon sudara: \[E_{\textrm{k}}=\frac{mv^{2}}{2}+\frac{mv^{2}}{2}=2\frac{mv^{2}}{2}=mv^{2}\] I prije i nakon sudara ukupna je kinetička energija: \[E_{\textrm{k}}=mv^{2}\]
Prema zakonu očuvanja količine gibanja, ukupna količina gibanja prije sudara jednaka je ukupnoj količini gibanja nakon sudara.
Ukupna količina gibanja prije sudara je:
\[m\vec{v}-m\vec{v}=\vec{0}\]
Prema tome, i nakon sudara će ukupna količina gibanja biti jednaka nuli.
Napomena
Ukoliko ne znate vektorski zapis fizičkih veličina, koristite se dogovorom: vektorska veličina je pozitivna ako ima orijentaciju osi \(x\), a negativna
ako je orijentirana u suprotnom smjeru osi \(x\).
Ukupna količina gibanja prije sudara je \(mv-mv=0\), a nakon sudara \(-mv+mv=0\).
3. zadatak
Duljina sekundne kazaljke na satu iznosi 8 cm, a duljina minutne kazaljke 10 cm. Kazaljke se
gibaju stalnim kutnim brzinama.
Koliki je omjer obodnih brzina točaka na vrhovima sekundne i minutne kazaljke?
- A. 48
- B. 50
- C. 60
- D. 75
Kutna brzina \(\omega\) jednaka je kutu kojega opiše kazaljka u jedinici vremena: \[\omega=\frac {\Delta \alpha}{\Delta t}\] Za vrijeme jednog okreta \(T\) kazaljka opiše puni kut od \(2\pi\,\textrm{rad}\), pa je kutna brzina jednaka: \[\omega=\frac {2\pi}{T}\] Kako je definirana obodna brzina?
Obodna brzina kod jednoliko kružnog gibanja jednaka je:
\[v=\frac {2r\pi}{T}\]
Ophodno vrijeme sekundne kazaljke je \(T_{\textrm{s}}=60\,\textrm{s}\), dok je ophodno vrijeme minutne kazaljke \(T_{\textrm{m}}=60\,\textrm{min}\).
Omjer obodnih brzina seknundne i minutne kazaljke je:
\[\frac {v_{\textrm{s}}}{v_{\textrm{m}}}=\frac{2r_{\textrm{s}}\pi}{T_{\textrm{s}}}\cdot \frac{T_{\textrm{m}}}{2r_{\textrm{m}}\pi}\]
\[\frac {v_{\textrm{s}}}{v_{\textrm{m}}}=\frac{2\cdot 0,08}{60}\cdot \frac{60\cdot 60}{2\cdot 0,1}=48\]
4. zadatak
Satelit jednoliko kruži u orbiti oko Zemlje polumjera \(R\) na visini \(h = R\) iznad njezine površine.
Koliko iznosi ubrzanje satelita ako je gravitacijsko ubrzanje pri površini Zemlje \(g\)?
- A. 0
- B. \(g/4\)
- C. \(g/2\)
- D. \(g\)
Gravitacijska sila kojom Zemlja privlači tijelo mase \(m\) udaljeno za \(r\) od njezinog središta može se prikazati izrazom: \[F=G\frac {Mm}{r^{2}}\] Masu Zemlje označili smo s \(M\), dok je \(G\) konstanta opće gravitacije.
Iz Newtonovog zakona gravitacije: \[F=G\frac {Mm}{r^{2}}\] vidimo da je gravitacijska sila u blizini površine Zemlje (\(r\approx R\) jednaka: \[F=G\frac {Mm}{R^{2}}\] Gravitacijsku silu možemo prikazati kao \(F=mg\) pa dobijemo: \[mg=G\frac {Mm}{R^{2}}\] Nakon skraćivanja s \(m\) vidimo da je gravitacijsko ubrzanje pri površini Zemlje jednako: \[g=G\frac {M}{R^{2}}\] Na visini \(h = R\) gravitacijsko ubrzanje \(g_{\textrm{h}}\) iznosi: \[g_{\textrm{h}}=G\frac {M}{\left (R+h \right )^{2}}=G\frac {M}{4R^{2}}\] \[\frac {g_{\textrm{h}}}{g}=G\frac {M}{4R^{2}}\cdot \frac{1}{G}\cdot\frac {R^{2}}{M}=\frac {1}{4}\] Konačno, \[g_{\textrm{h}}=\frac {g}{4}\]
5. zadatak
Kugla polumjera \(r\) miruje na stolu i ima neku temperaturu. Povećanjem temperature polumjer
kugle naraste za \(\Delta r\).
Povisuje li se središte kugle zbog opisane situacije i ako da, za koliko?
- A. \(\Delta r/2\)
- B. ne povisi se
- C. za \(\Delta r\)
- D. za \(2\Delta r\)
Pri zagrijavanju homogenog tijela njegov se volumen povećava u svim smjerovima jednako.
Neka je \(V_{0}\) volumen kugle pri početnoj temperaturi \(t_{0}\). Pri zagrijavanju kugle njezin se volumen povećava pa pri temperature \(t\) iznosi \(V\): \[V=V_{0}\left (1+\alpha\, \Delta t \right )\] Koeficijent volumnog toplinskog rastezanja \(\alpha\) tri puta je veći od koeficijenta linearnog toplinskog rastezanja \(\beta\): \[\alpha=3\beta\] Porast temperature pri zagrijavanju je: \[\Delta t=t-t_{0}\]
Pokrenite simulaciju.
Pri zagrijavanju tijela molekule titraju s većim amplitudama pa se zbog toga više udaljavaju od ravnotežnog položaja. To je razlog zašto se zagrijavanjem povećava međumolekularni prostor, odnosno, zašto se tijela šire. Međumolekularni prostor povećava se u svim smjerovima, zbog čega se središte zagrijane kugle povisi za \(\Delta r\).
6. zadatak
Koliko će se puta povećati temperatura idealnoga plina ako se srednja kvadratna brzina njegovih molekula poveća četiri puta?
- A. dva puta
- B. četiri puta
- C. osam puta
- D. šesnaest puta
Brzine pojedinačnih molekula u plinu su različite. Srednja kvadratna brzina (efektivna brzina) \(v_{\textrm{s}}\) je tipična brzina molekula pri
temperaturi \(T\):
\[v_{\textrm{s}}=\sqrt{\frac{3\,k\,T}{m_{0}}}\]
\(m_{0}\) - masa molekule plina
\(k\) - Boltzmannova konstanta
Kvadriranjem izraza za srednju kvadratnu brzinu: \[v_{\textrm{s}}=\sqrt{\frac{3\,k\,T}{m_{0}}}\] zaključujemo da je temperatura proporcionalna kvadratu srednje kvadratne brzine: \[T\sim v_{\textrm{s}}^{2}\] Ako se srednja kvadratna brzina poveća 4 puta, temperatura će se povećati 16 puta.
7. zadatak
Za povećanje temperature jedne zlatne kocke duljine brida \(a\) potrebna je količina topline \(Q\).
Kolika je količina topline potrebna da bi se drugoj zlatnoj kocki duljine brida \(2a\) temperatura povećala za isti iznos \(\Delta T\)?
Zanemarite gubitak topline u okolinu.
- A. \(Q\)
- B. \(2Q\)
- C. \(4Q\)
- D. \(8Q\)
Količina topline koju tijelo zagrijavanjem prima ili hlađenjem predaje može se prikazati izrazom:
\[Q=mc\Delta T\]
\(m\) - masa tijela
\(c\) - specifični toplinski kapacitet
\(\Delta T\) - promjena temperature (povećanje pri zagrijavanju, smanjenje pri hlađenju)
Obje kocke imaju jednak specifični toplinski kapacitet i jednaku gustoću, ali različit volumen i masu. \[Q=mc\Delta T=\rho Vc\Delta T\] \[Q=\rho a^{3}c\Delta T\] Brid druge kocke dva puta je veći pa je toplina koju kocka prima \(2^{3}=8\) puta veća.
8. zadatak
Graf prikazuje ovisnost termodinamičke temperature \(T\) vremenu zagrijavanja \(t\) pri prijelazu neke tvari iz čvrstoga agregacijskog stanja u plinovito agregacijsko stanje. Tvar se tijekom cijeloga vremena zagrijava izvorom topline čija se snaga ne mijenja.
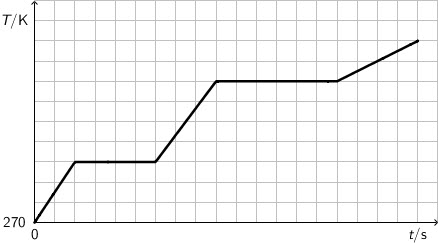
Koja je od navedenih tvrdnja ispravna?
- A. Najmanja promjena temperature događa se tijekom zagrijavanja tijela u tekućemu stanju.
- B. Najveća promjena temperature događa se tijekom zagrijavanja tijela u čvrstomu stanju.
- C. Specifični toplinski kapacitet tvari u tekućemu stanju manji je od specifičnoga toplinskog kapaciteta tvari u plinovitomu stanju.
- D. Specifična latentna toplina taljenja veća je od specifične latentne topline isparavanja.
Analizirajte toplinu koju tvar prima i promjenu temperature tvari pri:
- zagrijavanju tvari u čvrstom agregacijskom stanju
- prijelazu tvari iz čvrstog u tekuće agregacijsko stanje
- zagrijavanju tvari u tekućem agregacijskom stanju
- prijelazu tvari iz tekućeg u plinovito agregacijsko stanje
- zagrijavanju tvari u plinovitom agregacijskom stanju
Snaga izvora topline cijelo je vrijeme konstantna: \[P=\frac {Q}{t}\Rightarrow Q=Pt\] Prema tome, toplina koju tvar prima proporcionalna je vremenu zagrijavanja: \[Q\sim t\]
Pokrenite simulaciju. Iz grafa je vidljivo da je najmanja promjena temperature \(\Delta T_{3}\) pri zagrijavanju tvari u plinovitom agregacijskom stanju, a najveća \(\Delta T_{2}\) pri zagriavanju tvari u tekućem agregacijskom stanju. Prema tome, odgovori pod A. i B. nisu točni.
Toplina koju tvar prima za vrijeme zagrijavanja jednaka je: \[Q=mc\Delta T\] Za specifični toplinski kapacitet \(c\) dobijamo: \[c=\frac{Q}{m\Delta T}\] Iz zadanog grafa zaključujemo da je specifični toplinski kapacitet tvari u tekućem i u plinovitom agregacijskom stanju moguće prikazati kao: \[c_{\textrm{tekućina}}=\frac{Q_{3}}{m\Delta T_{2}}\] \[c_{\textrm{plin}}=\frac{Q_{5}}{m\Delta T_{3}}\] Podijelimo ova dva izraza: \[\frac{c_{\textrm{tekućina}}}{c_{\textrm{plin}}}=\frac{Q_{3}}{m\Delta T_{2}}\cdot \frac{m\Delta T_{3}}{Q_{5}}=\frac{Q_{3}}{Q_{5}}\cdot \frac{\Delta T_{3}}{\Delta T_{2}}\] Iz grafa vidimo da je \(Q_{3} \lt Q_{5}\) i \(\Delta T_{3} \lt \Delta T_{2}\). Oba razlomka su manja od jedan pa je i njihov umnožak manji od jedan. Prema tome: \[\frac{c_{\textrm{tekućina}}}{c_{\textrm{plin}}} \lt 1\] Točan je odgovor pod C.
9. zadatak
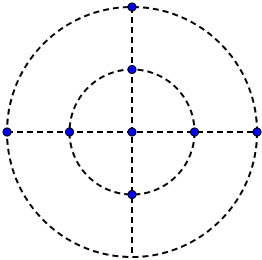
Na slici je prikazano osam jednakih naboja od 2 nC smještenih na kružnice polumjera 10 cm
i 20 cm.
Kolika je rezultantna električna sila na naboj u središtu koncentričnih kružnica?
- A. \(1,8\cdot 10^{-7}\,\textrm{N}\)
- B. \(9\cdot 10^{-7}\,\textrm{N}\)
- C. \(3,6\cdot 10^{-6}\,\textrm{N}\)
- D. \(0,9\,\textrm{N}\)
Rezultantu svih sila koje djeluju na naboj u središtu kružnica određujemo kao vektorski zbroj sila kojima naboji na kružnicama djeluju na naboj u središtu kružnica.
Svi su naboji jednako nabijeni pa će sile kojima djeluju na naboj u središtu biti odbojne. Iznos električne sile kojom svaki naboj djeluje na naboj u
središtu kružnica, prema Coulombovom zakonu, jednak je:
\[F=k\frac {q^{2}}{r^{2}}\]
Za naboje na unutarnjoj kružnici \(r=10\,\textrm{cm}\), dok je za naboje na vanjskoj kružnici \(r=20\,\textrm{cm}\).
Pokrenite prezentaciju.
10. zadatak
Paralelne ploče kondenzatora kapaciteta \(C_{0}\) između kojih je zrak priključene su na izvor stalnoga napona te je iznos naboja na pojedinoj ploči
jednak \(Q_{0}\). Između ploča toga kondenzatora stavi se dielektrik relativne permitivnosti 2 dok kondenzator ostaje spojen na isti izvor napona.
Koliko iznose kapacitet kondenzatora i naboj na pojedinoj ploči kondenzatora?
- A. \(C=C_{0}/2\) i \(Q=2Q_{0}\)
- B. \(C=2C_{0}\) i \(Q=Q_{0}/2\)
- C. \(C=C_{0}/2\) i \(Q=Q_{0}/2\)
- D. \(C=2C_{0}\) i \(Q=2Q_{0}\)
Čemu je jednak kapacitet pločastog kondenzatora bez dielektrika i sa dielektrikom? Ukoliko se ne možete sjetiti, potražite te izraze u knjižici formula. Kako određujemo naboj na svakoj ploči ako je kondenzator priključen na izvor napona \(U\)?
Kapacitet pločastog kondenzatora bez dielektrika je: \[C_{0}=\varepsilon_{0}\frac {S}{d}\] Kapacitet pločastog kondenzatora sa dielektrikom je: \[C=\varepsilon_{0}\varepsilon_{r}\frac {S}{d}\] Podijelimo drugi izraz s prvim: \[\frac {C}{C_{0}}=\frac {\varepsilon_{0}\varepsilon_{r}}{\varepsilon_{0}}\cdot \frac{S}{d}\cdot \frac {d}{S}=\varepsilon_{r}=2\] \[C=2C_{0}\] Naboj na pločama kondnzatora bez dielektrika i sa dielektrikom iznosi: \[Q_{0}=C_{0}U\] i \[Q=CU\] Podijelimo drugi izraz s prvim: \[\frac {Q}{Q_{0}}=\frac {CU}{C_{0}U}=\frac {C}{C_{0}}=2\] \[Q=2Q_{0}\] Prema tome, točan odgovor je D.
11. zadatak
Kada se neki otpornik spoji na izvor napona, strujnim krugom prolazi struja \(I\).
Koji od ponuđenih načina spajanja otpornika jednakih otpora dovodi do toga da ukupna struja kroz strujni krug iznosi \(4I\) ?
- A. dva otpornika serijski
- B. četiri otpornika serijski
- C. dva otpornika paralelno
- D. četiri otpornika paralelno
Primijenite Ohmov zakon.
Struja koja prolazi strujnim krugom, prema Ohmovom zakonu jednaka je: \[I=\frac {U}{R}\] Da bi se struja povećala četiri puta, otpor se mora smanjiti četiri puta. Serijskim spajanjem otpornika ukupni se otpor povećava pa prema tome potrebno je paralelno spojiti četiri jednaka otpornika \(R\). \[\frac {1}{R_{\textrm{uk}}}=\frac {1}{R}+\frac {1}{R}+\frac {1}{R}+\frac {1}{R}=\frac {4}{R}\] Ukupni otpor je: \[{R}_{\textrm{uk}}=\frac{R}{4}\] Iz Ohmovog zakona \[I_{\textrm{uk}}=\frac {U}{R_{\textrm{uk}}}=4\frac{U}{R}=4I\] zaključujemo da će u tom slučaju struja biti četiri puta veća.
12. zadatak
Učenik je od zavojnice napravio elektromagnet tako da ju je priključio na izvor napona.
Što od navedenoga treba napraviti učenik kako bi se smanjilo magnetsko polje unutar zavojnice?
- A. povećati struju koja prolazi zavojnicom
- B. povećati broj namotaja zavojnice
- C. rastegnuti zavojnicu
- D. umetnuti željeznu jezgru unutar zavojnice
Kojim se izrazom prikazuje magnetsko polje unutar zavojnice?
Magnetsko polje unutar zavojnice sa \(N\) namotaja, kojoj je duljina \(\ell\) i kroz koju prolazi električna struja \(I\) jednako je: \[B=\mu_{0} \mu_{\textrm{r}}\frac {NI}{\ell}\] Magnetsko polje unutar zavojnice će se smanjiti ako povećamo njezinu duljinu \(\ell\), odnosno ako ju rastegnemo.
13. zadatak
Elongacija tijela koje harmonijski titra na opruzi konstante elastičnosti 2,5 N/m dana je izrazom \[x=4\,\textrm{cm}\,\textrm{sin}\left(1,57\,\textrm{s}^{-1}\,t\right).\] Kolika je maksimalna kinetička energija tijela?
- A. 2 mJ
- B. 20 mJ
- C. 2 J
- D. 20 J
Kojim izrazom prikazujemo ukupnu energiju harmonijskog oscilatora? Čemu je jednaka maksimalna elastična potencijalna energija, a čemu maksimalna kinetička energija?
Ukupna energija harmonijskog oscilatora jednaka je zbroju njegove elastične potencijalne energije:
\[E_{\textrm{elp}}=\frac{1}{2}kx^{2}\]
i kinetičke energije:
\[E_{\textrm{k}}=\frac{1}{2}mv^{2}\]
\[E=E_{\textrm{elp}}+E_{\textrm{k}}\]
Pokrenite simulaciju.
U amplitudnom položaju (\(x=-x_{0}\) i \(x=+x_{0}\)) elastična potencijalna energija ima maksimalnu vrijednost, dok je kinetička energija jednaka nuli:
\[E_{\textrm{elp,maks}}=\frac{1}{2}kx_{0}^{2}; E_{\textrm{k}}=0\]
Ukupna energija u amplitudnom položaju je:
\[E_{1}=\frac{1}{2}kx_{0}^{2}+0\]
\[E_{1}=\frac{1}{2}kx_{0}^{2}\]
U ravnotežnom položaju (\(x=0\)) elastična potencijalna energija jednaka je nuli, dok kinetička energija ima maksimalnu vrijednost:
\[E_{\textrm{elp}}=0; E_{\textrm{k,maks}}=\frac{1}{2}mv_{0}^{2}\]
Ukupna energija u ravnotežnom položaju je:
\[E_{2}=0+\frac{1}{2}mv_{0}^{2}\]
\[E_{2}=\frac{1}{2}mv_{0}^{2}\]
Ako zanemarimo sve pretvorbe mehaničke energije u druge oblike, ukupna energija harmonijskog oscilatora bit će očuvana:
\[E_{1}=E_{2}\]
\[\frac{1}{2}kx_{0}^{2}=\frac{1}{2}mv_{0}^{2}\]
Prema tome, ukupna energija harmonijskog oscilatora jednaka je maksimalnoj potencijalnoj energiji, odnosno maksimalnoj kinetičkoj energiji:
\[E=\frac{1}{2}kx_{0}^{2}\]
\[E=\frac{1}{2}mv_{0}^{2}\]
Maksimalna kinetička energija jednaka je maksimalnoj elastičnoj potencijalnoj energiji:
\[E_{\textrm{k,maks}}=E_{\textrm{elp,maks}}\]
odnosno:
\[E_{\textrm{k,maks}}=\frac{1}{2}kx_{0}^{2}\]
Pomoću simulacije provjerite svoj odgovor.
14. zadatak
Matematičko njihalo izvodi harmonijsko titranje.
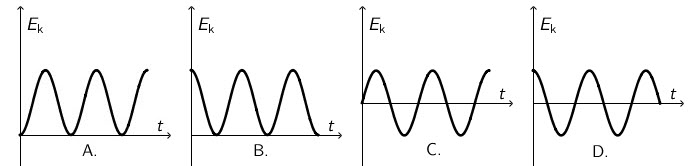
Koji graf ispravno prikazuje ovisnost kinetičke energije o vremenu ako se u početnome trenutku njihalo nalazilo u ravnotežnome položaju?
- A. graf A
- B. graf B
- C. graf C
- D. graf D
U kojem se položaju nalazi kuglica matematičkog njihala ako joj je kinetička energija maksimalna? Kako ovisi kinetička energija kuglice o elongaciji?
Ako elongaciju harmonijskog titranja prikazujemo kao: \[y=y_{0}\,\textrm{sin}\,\omega t\] brzinu prikazujemo kao: \[v=\omega \, y_{0}\,\textrm{cos}\,\omega t\] Kinetička energija tada je jednaka: \[E_{\textrm{k}}=\frac {1}{2}m\,v^{2}=\frac {1}{2}m\,\omega ^{2}\,y_{0}^{2}\,\textrm{cos}^{2}\omega t\] Kinetička energija ne može imati negativnu vrijednost pa grafovi C. i D. nisu točni.
U ravnotežnom položaju kinetička energija kuglice matematičkog njihala je najveća. To odgovara grafu B.
15. zadatak
Koja od navedenih jednadžba opisuje harmonijski val brzine 5 m/s, perioda 0,16 s i amplitude 30 cm?
- A. \(y=0,3\,\textrm{m}\,\textrm{sin}\,\pi\left (0,16\,\textrm{s}^{-1}\,t-5\,\textrm{m}^{-1}\,x\right)\)
- B. \(y=0,3\,\textrm{m}\,\textrm{sin}\,\pi\left (12,5\,\textrm{s}^{-1}\,t-2,5\,\textrm{m}^{-1}\,x\right)\)
- C. \(y=0,3\,\textrm{m}\,\textrm{sin}\,\pi\left (12,5\,\textrm{s}^{-1}\,t-0,064\,\textrm{m}^{-1}\,x\right)\)
- D. \(y=0,3\,\textrm{m}\,\textrm{sin}\,\pi\left (0,32\,\textrm{s}^{-1}\,t-2,5\,\textrm{m}^{-1}\,x\right)\)
Kojom se jednadžbom prikazuje harmonijski val? Kako pomoću podataka iz zadatka određujemo valnu duljinu?
Jednadžba harmonijskog vala: \[y=y_{0}\, \textrm{sin}\left ( \frac{2\pi }{T}t - \frac{2\pi }{\lambda}x\right)\]
Podaci iz zadatka:
- \(y_{0}=30\,\textrm{cm}=0,3\,\textrm{m}\)
- \(T=0,16\,\textrm{s}\)
- \(\lambda=v\,T=0,8\,\textrm{m}\)
Uvrstimo podatke u jednadžbu vala: \[y=0,3\, \textrm{sin}\left ( \frac{2\pi }{0,16}t - \frac{2\pi }{0,8x}\right )\] \[y=0,3\,\textrm{m}\, \textrm{sin}\left ( 12,5\pi \,\textrm{s}^{-1} t - 2,5\pi \,\textrm{m}^{-1} x\right )\]
16. zadatak
Koje se svojstvo zvučnoga vala ne mijenja kada val prelazi iz zraka u vodu?
- A. valna duljina
- B. frekvencija
- C. brzina
- D. amplituda
Što se događa s brzinom kada val prelazi iz jednog sredstva u drugo?
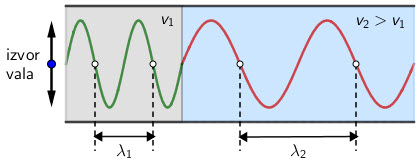
Brzina vala ovisi o svojstvima sredstva kroz koje se val širi.
Kada val prelazi iz jednog sredstva u drugo, mijenja se njegova brzina pa prema tome i valna duljina.
\[\lambda=\frac {v}{f}\]
Frekvencija vala, koja je jednaka frekvenciji titranja izvora, ne mijenja se. Zvuk je također val pa to vrijedi i za njega.
17. zadatak
Dva koherentna vala svjetlosti upadaju na zastor u istoj točki koja je osvijetljena.
Koja od navedenih veličina ne može biti fazna razlika valova?
- A. \(0\)
- B. \(\pi\)
- C. \(3\pi/2\)
- D. \(2\pi\)
Kolika mora biti razlika hoda \(\Delta x\), a kolika razlika faza \(\Delta \varphi\) da se valovi interferencijom potpuno ponište?
Pomoću apleta na stranici
Interferencija valova
pronađite odgovor.
Napomena
Potvrdite sva tri potvrdna okvira pa pomoću klizača \(\Delta \varphi\) odaberite odgovore ponuđene u zadatku.
- Destruktivna interferencija (valovi se potpuno poništavaju) \[\Delta \varphi=\left (2k+1 \right)\pi\] \[\Delta x=\left (2k+1\right )\frac{\lambda}{2}\] \[k=0,1,2\;...\]
- Konstruktivna interferencija (valovi se maksimalno pojačavaju) \[\Delta \varphi=2k\pi\] \[\Delta x=k\lambda\] \[k=0,1,2\;...\]
- U ostalim slučajevima valovi se interferencijom djelomično pojačavaju ili djelomično poništavaju.
18. zadatak
Realan predmet nalazi se ispred sustava dviju tankih leća. Prva leća \(L_{1}\) stvara umanjenu realnu
sliku, dok druga leća \(L_{2}\) stvara virtualnu i uvećanu sliku.
Kakve su leće \(L_{1}\) i \(L_{2}\)?
- A. \(L_{1}\) konvergentna leća i \(L_{2}\) je konvergentna leća.
- B. \(L_{1}\) konvergentna leća, a \(L_{2}\) je divergentna leća.
- C. \(L_{1}\) je divergentna leća, a \(L_{2}\) je konvergentna leća.
- D. \(L_{1}\) divergentna leća i \(L_{2}\) je divergentna leća.
Pomoć potražite na poveznici Konvergentne i divergentne leće.
Divergentna leća za bilo koji položaj predmeta stvara uspravnu, umanjenu i virtualnu sliku. Prema tome, obje leće su konvergentne.
19. zadatak
Ura u mirovanju otkucava svake sekunde, a nalazi se u svemirskome brodu vlastite duljine 100 m.
Svemirski brod se u odnosu na mirnoga promatrača giba brzinom 0,6c.
Koliki će vremenski interval između dvaju otkucaja ure i koliku će duljinu svemirskoga broda mjeriti mirni promatrač?
- A. manje od 1 s, manje od 100 m
- B. manje od 1 s, više od 100 m
- C. više od 1 s, manje od 100 m
- D. više od 1 s, više od 100 m
Pomoć potražite na poveznici Kontrakcija duljine i dilatacija vremena
Dilatacija vremena
Interval vremena kojega mjeri promatrač u odnosu na kojega ura miruje označujemo s \(\Delta t_{0}\) i nazivamo ga vlastiti interval vremena.
(Taj vremenski interval mjere putnici u svemirskom brodu.)
Interval vremena kojega mjeri promatrač u odnosu na koega se ura u svemirskom brodu giba mjeri interval vremena \(\Delta t\).
\[\Delta t=\frac{\Delta t_{0}}{\sqrt{1-v^{2}/c^{2}}}\]
Za mirnog promatrača interval vremena bit će veći od 1 s.
Kontrakcija duljine
Duljinu svemirskog broda u sustavu u kojemu svemirski brod miruje označujemo s \(L_{0}\) i nazivamo vlastita duljina. (Toliku će duljinu izmjeriti
putnici u svemirskom brodu.)
Duljinu svemirskog broda koju mjeri mirni promatrač označujemo s \(L\).
\[L=L_{0}\sqrt{1-v^{2}/c^{2}}\]
Duljina svemirskog broda za promatrača koji miruje bit će manja od 100 m.
20. zadatak
Dvije čestice masa \(m_{1}\) i \(m_{2}\) imaju jednake kinetičke energije.
Kako se odnose njihove valne duljine ako je masa prve čestice \(m_{1}\) dvostruko veća od mase druge čestice \(m_{2}\)?
- A. \(\lambda_{1}=2\lambda_{2}\)
- B. \(\lambda_{1}=\lambda_{2}\)
- C. \(\lambda_{1}=\lambda_{2}/\sqrt{2}\)
- D. \(\lambda_{1}=\lambda_{2}/2\)
Prikažte kinetičku energiju čestice \[E_{k}=\frac{mv^{2}}{2}\] pomoću de Broglieve valne duljine: \[\lambda=\frac{h}{mv}=\frac{h}{p}\]
Izraz za kinetičku energiju čestice proširimo sa masom čestice \(m\): \[E_{k}=\frac{m^{2}v^{2}}{2m}\] Uzmemo li u obzir količinnu gibanja \(p=mv\), kinetičku energiju prikazujemo kao: \[E_{k}=\frac{p^{2}}{2m}\] Uvrstimo količinu gibanja iz de Broglieve relacije: \[p=\frac{h}{\lambda}\] Kinetička energija čestice izražena pomoću de Broglieve valne duljine: \[E_{k}=\frac{1}{2m}\cdot \frac{h^{2}}{\lambda^{2}}\Rightarrow \lambda^{2}=\frac{1}{2m}\cdot \frac{h^{2}}{E_{k}}\] \[\lambda_{1}^{2}=\frac{1}{2m_{1}}\cdot \frac{h^{2}}{E_{k}}\] \[\lambda_{2}^{2}=\frac{1}{2m_{2}}\cdot \frac{h^{2}}{E_{k}}\] Podijelimo ova dva izraza: \[\frac{\lambda_{1}^{2}}{\lambda_{2}^{2}}=\frac{m_{2}}{m_{1}}=\frac{m_{2}}{2m_{2}}=\frac{1}{2}\] \[\frac{\lambda_{1}}{\lambda_{2}}=\frac{1}{\sqrt{2}}\] \[\lambda_{1}=\frac{\lambda_{2}}{\sqrt{2}}\]
21. zadatak
Koji izotop označen s X nastaje u nuklearnoj reakciji \[{_{}^{26}}\textrm{Al}+\textrm{n}\rightarrow \textrm{p}+\textrm{X}\]
- A. \({_{}^{26}}\textrm{Mg}\)
- B. \({_{}^{27}}\textrm{Mg}\)
- C. \({_{}^{26}}\textrm{Al}\)
- D. \({_{}^{27}}\textrm{Al}\)
Pomoć potražite na poveznici Nuklearne reakcije
Jednadžbu nuklearne reakcije zapišimo u obliku: \[{_{13}^{26}}\textrm{Al}+{_{0}^{1}}\textrm{n}\rightarrow {_{1}^{1}}\textrm{p}+{_{Z}^{A}}\textrm{X}\] Primijenimo zakon očuvanja električnog naboja: broj protona prije reakcije jednak je broju protona nakon reakcije: \[13+0=Z+1\Rightarrow Z=12\] i zakon očuvanja broja nukleona: broj nukleona prije reakcije jednak je broju nukleona nakon reakcije: \[26+1=1+A\Rightarrow A=26\] U periodnom sustavu vidimo da se radi o izotopu magnezija \({_{12}^{26}}\textrm{Mg}\).
22. zadatak
Za potrebe medicinskih pretraga liječnik je naručio 10 g radioaktivnoga izotopa Tc-99 čije je vrijeme poluraspada
6 sati.
Koliko su toga radioaktivnog izotopa u tvornici trebali isporučiti da bi liječnik dobio naručenu količinu ako dostava traje 18 sati?
- A. 160 g
- B. 80 g
- C. 40 g
- D. 20 g
Pomoć potražite na poveznici Zakon radioaktivnog raspada
Zakon radioaktivnog raspada
\[N=N_{0}\cdot 2^{\mathbf{-}\large{\frac{t}{T}}}\]
- \(N_{0}\) - broj neraspadnutih jezgara u početnom trenutku
- \(N\) - broj neraspadnutih jezgara nakon vremena \(t\)
- \(T\) - vrijeme poluraspada
Masa uzorka proporcionalna je broju jezgara: \[m=m_{0}\cdot 2^{\mathbf{-}\large{\frac{t}{T}}}\] Pomnožimo ovaj izraz s \[2^{\large{\frac{t}{T}}}\] Tvornica je trebala isporučiti radioaktivni uzorak kojemu je masa: \[m_{0}=m\cdot 2^{\large{\frac{t}{T}}}=10\cdot 2^{\large{\frac{18}{6}}}=10\cdot 2^{3}=80\,\textrm{g}\]
23. zadatak
Neki komad radioaktivnoga materijala sastoji se od samo jednoga izotopa.
Koji od navedenih radioaktivnih raspada neće promijeniti atomski broj izotopa?
- A. \(\alpha\)-raspad
- B. \(\beta^{-}\)-raspad
- C. \(\beta^{+}\)-raspad
- D. \(\gamma\)-raspad
Pomoć potražite na poveznici Gama-radioaktivnost
Gama-raspad
Ponekad jezgra nakon emisije alfa ili beta-čestica ostane u pobuđenom stanju u kojemu joj je energija veća od energije osnovnog stanja. (U osnovnom stanju jezgra ima najmanju energiju.) Jezgra ne može ostati dugo u pobuđenom stanju, nego spontano prelazi u stanja niže energije sve do osnovnog. Pri tim prijelazima jezgra emitira elektromagnetske valove, odnosno gama-fotone vrlo kratkih valnih duljina, pri čemu ne dolazi do promjene u građi jezgre , nego joj se smanjuje energija. To smanjenje energije jezgre jednako je energiji emitiranog gama-fotona.
Prema tome, pri gama-raspadu ne dolazi do promjene ni atomskog broja \(Z\) niti masenog broja \(A\).
24. zadatak
Pretpostavite da elektron kruži oko jezgre u skladu s Bohrovim modelom atoma po putanji u kojoj ima najnižu energiju.
Kakvi su polumjer putanje i brzina elektrona pri kruženju po toj putanji?
- A. Polumjer je najmanji, a brzina je najveća.
- B. Polumjer i brzina su najmanji.
- C. Polumjer je najveći, a brzina je najmanja.
- D. Polumjer i brzina su najveći.
Pomoć potražite na poveznici Bohrov model atoma
Prema Bohrovom modelu atoma, elektron ima najnižu energiju kada kruži po kružnici kojoj odgovara kvantni broj \(n=1\): \[E_1=\mathbf{-}13,6\ \textrm{eV}\] To stanje nazivamo osnovnim stanjem atoma. Polumjer prve kružnice je: \[r_1=5,29\cdot{10}^{\mathbf{-}11}\ \textrm{m}\] Polumjeri ostalih kružnica su veći (\(n=2, 3, 4, 5\;...\)): \[r_n=r_1{\cdot n}^2\]
Brzina elektrona u osnovnom stanju je: \[v_1=2,18\cdot{10}^6\ \textrm{m}/\textrm{s}\] U ostalim dopuštenim kružnicama (\(n=2, 3, 4, 5\;...\)) brzina elektrona je manja: \[v_n=\frac{v_1}{n}\]
25. zadatak
Balon punjen helijem temperature \(35\,^{0}\textrm{C}\) pri tlaku \(2p\) ima volumen \(3\, \textrm{m}^{3}\).
Koliki je volumen balona na visini gdje je temperatura \(-20\,^{0}\textrm{C}\), a tlak \(p/2\)? Pretpostavite da se helij ponaša kao idealan plin.
Odgovor: \(\textrm{m}^{3}\)
Kako prikazujemo jednadžbu stanja idealnog plina koji se nalazi u zatvorenoj posudi?
Pomoć potražite na poveznici
Jednadžba stanja idealnog plina.
Jednadžba stanja idealnog plina koji se nalazi u zatvorenom balonu (plin ne može ulaziti ni izlaziti iz balona): \[\frac{p_{1}V_{1}}{T_{1}}= \frac{p_{2}V_{2}}{T_{2}}\] Volumen plina \(V_{2}\) pri temperaturi \(-20\,^{0}\textrm{C}\) i tlaku \(p_{2}=p/2\) jednak je: \[V_{2}=\frac{p_{1}V_{1}T_{2}}{p_{2}T_{1}}=\frac{p_{1}}{p_{2}}\cdot V_{1}\cdot \frac{T_{2}}{T_{1}}=4\cdot 3 \cdot \frac {253}{308}=9,86\,\textrm{m}^{3}\] Temperaturu smo pretvorili u kelvine.
26. zadatak
Predmet je udaljen 20 cm od središta divergentne leće jakosti -5 dpt.
Koliko je udaljena slika predmeta od leće?
Napomena:
U zadatku objavljenom na stranicama NCVVO izostavljen je predznak minus.
Odgovor:
Primijenite jednadžbu divergentne leće. Kako je definirana jakost leće?
Pomoć potražite na poveznicama:
Divergentna leća.
Jednadžba divergentne leće.
Jakost leće \(C\) jednaka je recipročnoj vrijednosti žarišne udaljenosti \(f\) izražene u metrima: \[C=\frac{1}{f}\] Odredimo žarišnu daljinu: \[f=\frac{1}{C}=\frac{1}{-5}=-0,2\, \textrm{m}=-20\, \textrm{cm}\] Primijenimo jednadžbu leće: \[\frac{1}{a}+\frac{1}{b}=\frac{1}{f}\Rightarrow \frac{1}{b}=\frac{1}{f}-\frac{1}{a}\] \[\frac{1}{b}=\frac{1}{-20}-\frac{1}{20}=\frac{-2}{20}\] \[b=-10\,\textrm{cm}\]
27. zadatak
Čovjek stoji na dasci za stojeće veslanje volumena 185 litara. Jedna polovina volumena daske iznad je površine vode
gustoće \(1030\, \textrm{kg/m}^{3}\).
Kolika je ukupna težina čovjeka i daske?
Odgovor:
Uzgon je sila koja djeluje na tijelo uronjeno u fluid i koja je suprotno orijentirana od sile teže: \[F_{\textrm{u}}=\rho g V_{\textrm{udt}}\]
- \(\rho\) - gustoća fluida (u ovom zadatku je to gustoća vode)
- \(V_{\textrm{udt}}\) - volumen uronjenog dijela tijela
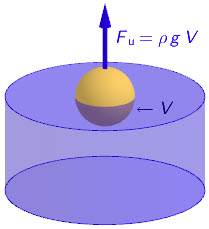
Daska i čovjek koji na njoj stoji plivaju na vodi. To znači da je uzgon po iznosu jednak težini čovjeka i daske. Daska je do polovine uronjena u vodu pa će uzgon djelovati samo na polovinu volumena daske. Sila teža djelovat će na cijelu dasku i čovjeka koji na njoj stoji.
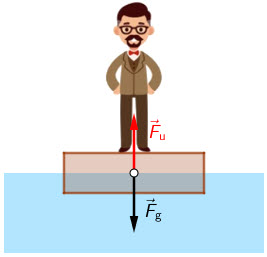
\[F_{\textrm{g}}=\rho g \cdot \frac{V}{2}\] Volumen pretvorimo u \(\textrm{m}^{3}\) pa za rezultat dobijemo: \[F_{\textrm{g}}=1030\cdot 10 \cdot \frac{185\cdot 10^{-3}}{2}=952,75 N\]
28. zadatak
U zatvorenoj posudi s pomičnim klipom nalaze se 2 mola idealnoga plina temperature \(20\,^{0}\textrm{C}\)
i volumena \(25\,\ell\). Plin se izobarno zagrijava i pritom obavi rad 3 kJ.
Kolika je promjena volumena idealnoga plina u tome procesu?
Odgovor: \(\textrm{m}^{3}\)
Primijenite jednadžbu stanja idealnog plina i rad plina pri izobarnom širenju.
Pomoću jednadžbe stanja idealnog plina \[pV=nRT\] odredimo tlak plina (volumen pretvorimo u kubne metre, a temperaturu u kelvine): \[p=\frac{nRT}{V}=\frac{2\cdot 8,314 \cdot 293}{25\cdot 10^{-3}}=194880,16\textrm{Pa}\] Rad plina pri izobarnom širenju: \[W=p\Delta V\Rightarrow\Delta V=\frac{W}{p}=1,54\cdot 10^{-2}\,\textrm{m}^{3}\] (U polje za odgovor znanstveni zapis bilježimo kao 1,54E-2)
29. zadatak
Naboj \(q\) iznosa 1 nC fiksiran je u ishodištu. Drugi naboj istoga iznosa nalazi se u točki u kojoj
je vrijednost električnoga potencijala prvoga naboja 2 V. Taj se naboj pusti u slobodno gibanje.
Kolika mu je kinetička energija nakon što je prešao 4,5 m?
Odgovor:
Električna potencijalna energija, potencijal i napon
Električna potencijalna energija dva točkasta naboja \(q\) i \(q'\), koji su udaljeni \(r\) jedan od drugog, iznosi: \[E_{\textrm{ep}}=k\frac{q\,q'}{r}\]
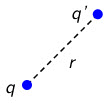
Promjena električne potencijalne energije pri gibanju naboja \(q'\) iz točke A u točku B jednaka je negativnom radu električne sile koja pri tom gibanju djeluje na naboj \(q'\): \[\Delta E_{\textrm{ep}}=-W\]
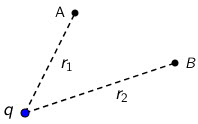
Slika 1.
Taj je rad jednak: \[W=-\left ( E_{\textrm{ep,B}}-E_{\textrm{ep,A}} \right )\] \[W=\left ( E_{\textrm{ep,A}}-E_{\textrm{ep,B}} \right )\] \[W=k\frac{q\,q'}{r_{1}}-k\frac{q\,q'}{r_{2}}\qquad(1)\]
Električni potencijal u nekoj točki električnog polja jednak je električnoj potencijalnoj energiji jediničnog naboja u toj točki: \[\varphi=\frac{E_{\textrm{ep}}}{q'}\] \[\varphi=k\frac{q}{r}\]
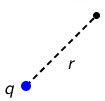
Rad električne sile, uzevši u obzir izraz (1), možemo prikazati i pomoću potencijala: \[W=q'\left (\varphi_{\textrm{A}}-\varphi_{\textrm{B}}\right )\] Razliku potencijala između točaka A i B zovemo napon, kojeg označujemo s \(U\) (Slika 1.): \[U=\varphi_{\textrm{A}}-\varphi_{\textrm{B}}\] Rad kojega obavi električno polje pri premještanju naboja \(q'\) iz točke A u točku B prikazujemo i pomoću napona između točaka A i B (Slika 1.): \[W=q'\,U\]
Pretpostavimo da su naboji \(q\) i \(q'\) pozitivni. Koliki rad obavi vanjska sila pri premještanju naboja \(q'\) iz točke A u točku B (Slika 1.)? Taj je rad jednak promjeni električne potencijalne energije: \[W=\left ( E_{\textrm{ep,B}}-E_{\textrm{ep,A}} \right )\] \[W=k\frac{q\,q'}{r_{2}}-k\frac{q\,q'}{r_{1}}\] Taj rad prikazujemo i pomoću potencijala: \[W=q'\left (\varphi_{\textrm{B}}-\varphi_{\textrm{A}}\right )\]
Napomena
Potencijal je skalarna veličina pa može biti pozitivan ili negativan pa pri računanju moramo uzeti u obzir i predznak naboja. Isto vrijedi i za
električnu potencijalnu energiju.
Pokrenite simulaciju i kliknite na dugme Naprijed.
30. zadatak
Svjetlost valne duljine 400 nm upada na metalnu ploču sačinjenu od materijala čiji je izlazni rad
2 eV.
Kolika je kinetička energija elektrona koji izlaze iz metala?
Odgovor:
Ako foton koji padne na metal pogodi elektron, predaje mu svoju energiju. Dio te energije pretvara se u rad za svladavanje energije vezanja \(W_{\textrm{i}}\), a dio u kinetičku energiju fotoelektrona: \[E_{\textrm{f}}=W_{\textrm{i}}+E_{\textrm{k}}\] Kinetička energija izbačenog elektrona jednaka je: \[E_{\textrm{k}}=hf - W_{\textrm{i}}\] Frekvencija upadnog zračenja jednaka je \(f=c/\lambda\) pa je kinetička energija jednaka: \[E_{\textrm{k}}=\frac{hc}{\lambda}-W_{\textrm{i}}=1,77\cdot 10^{-19}\,\textrm{J}=1,11\,\textrm{eV}\] Napomenimo da se u svim izrazima radi o najvećoj kinetičkoj energiji emitiranih fotoelektrona. Svi elektroni nemaju jednaku \(E_{\textrm{k}}\), pogotovo oni koji se nalaze daleko od površine metala jer na svom putu prema površini metala gube dio energije na sudare s atomima.
31. zadatak
Tijelo mase 10 kg miruje na dnu kosine duljine 20 m i nagiba \(60\,^{0}\). Na tijelo počinje
djelovati vučna sila od 120 N, paralelno uz kosinu. Koeficijent trenja između tijela i podloge jest 0,2.
Nakon koliko će vremena tijelo stići na vrh kosine?
Odgovor:
Koje sile djeluju na tijelo? Odredite rezultantnu silu, primijenite temeljni zakon gibanja kako biste odredili akceleraciju, a zatim pomoću puta i akceleracije odredite vrijeme.
Pokrenite simulaciju i kliknite na dugme \(\,>\,\).
32. zadatak
Kovanica je gurnuta po horizontalnoj površini stola visokoga 80 cm početnom brzinom 10 m/s.
Kovanica prijeđe 1 m klizeći po stolu, odleti preko njegova ruba i padne na pod. Faktor trenja između kovanice i stola jest 0,2.
Zanemarite otpor zraka.
Kolika je brzina kovanice neposredno prije udara o pod?
Odgovor:
Primijenite zakon očuvanja energije.
Pokrenite simulaciju i kliknite na Pokreni.
Energija u početnom trenutku, \(E_{1}\), pretvara se u rad za svladavanje sile trenja i u energiju \(E_{2}\) neposredno prije nego kovanica počne padati sa stola: \[E_{1}=W_{t}+E_{2}\] \[\frac{m\,v_{1}^{\,2}}{2}+m\,g\,h=\mu\,m\,g\,s+\frac{m\,v_{2}^{\,2}}{2}+m\,g\,h\] Brzinu \(v_{2}\) kojom kovanica sleti sa stola moguće je odrediti nakon što pojednostavimo prethodni izraz: \[v_{1}^{\,2}=2\,\mu\,g\,s+v_{2}^{\,2}\Rightarrow v_{2}^{\,2}=v_{1}^{\,2}-2\,\mu\,g\,s\qquad(1)\]
Otpor zraka zanemarujemo pa je energija kovanice u trenutku slijetanja sa stola jednaka energiji neposredno prije pada na tlo: \[E_{2}=E_{3}\] \[\frac{m\,v_{3}^{\,2}}{2}=\frac{m\,v_{2}^{\,2}}{2}+m\,g\,h\] Nakon sređivanja ovog izraza dobivamo: \[v_{3}^{\,2}=v_{2}^{\,2}+2\,g\,h\qquad(2)\] U izraz (2) uvrstimo izraz (1): \[v_{3}^{\,2}=v_{1}^{\,2}-2\,\mu\,g\,s+2\,g\,h\] Brzina kovanice neposredno prije pada na tlo: \[v_{3}^{\,}=\sqrt{v_{1}^{\,2}-2\,g\left (\mu\,s-h\right )}=10,58\,\frac{\textrm{m}}{\textrm{s}}\]
33. zadatak
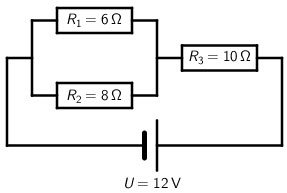
Tri otpornika \(R_{1}\), \(R_{2}\) i \(R_{3}\) spojeni su na izvor napona \(U\) kao na slici.
Kolika je snaga na otporniku \(R_{3}\)?
Odgovor:
Električnu snagu koja se razvija na otporniku prikazujemo kao: \[P=U\,I\] Za rješenje zadatka trebat će nam još i Ohmov zakon za dio strujnog kruga: \[U=I\,R\]
Odredimo ukupan otpor strujnog kruga. Otpornici \(R_{1}\) i \(R_{2}\) spojeni su paralelno pa je njihov ukupan otpor: \[\frac{1}{R_{12}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}\Rightarrow R_{12}=3,429\,\Omega\] Otpori \(R_{12}\) i \(R_{3}\) spojeni su serijski pa je ukupni otpor strujnog kruga: \[R=R_{12}+R_{3}=13,429\,\Omega\] Struja koja prolazi krugom je: \[I=\frac{U}{R}=0,894\,\textrm{A}\] Ta struja prolazi kroz otpor \(R_{3}\). Snaga na tom otporu je: \[P=U\,I=I^{2}R_{3}=7,99\,\textrm{W}\]
34. zadatak
Nabijena čestica ulazi u homogeno magnetsko polje iznosa 0,5 T okomito na silnice polja koje izlaze iz površine papira i pritom opisuje polukružnu putanju kao na slici. Masa čestice iznosi \(2,7\cdot 10^{‒30}\, \textrm{kg}\), a naboj \(9,6 \cdot 10^{‒19}\, \textrm{C}\).
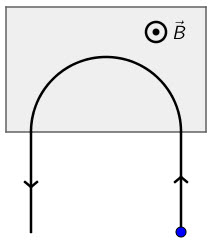
1. Je li čestica pozitivno ili negativno nabijena?
Čestica je nabijena.
2. Koliko se dugo čestica nalazi u tome magnetskom polju?
Odgovor:
Na naboj koji se u magnetskom polju giba djeluje Lorentzova sila. Kako određujemo smjer te sile ako je naboj negativan, a kako ako je pozitivan?
Koja sila ima ulogu centripetalne sile dok se naboj u magnetskom polju giba po polukružnici?
Pokrenite simulaciju. Pomoću pokazivača miša pomjerajte negativni naboj po polukružnici. Lorentzova sila je okomita na vektor brzine i vektor magnetskog polja, a usmjerena je prema središtu polukružnice. Iznos Lorentzove sile je: \[F_{\small{\textrm{L}}}=q\,v\,B\,\textrm{sin}\,\alpha\] Vektori \(v\) i \(B\) su okomiti pa je \(\textrm{sin}\,\alpha=1\). Lorentzovu silu u ovom primjeru možemo prikazati kao: \[F_{\small{\textrm{L}}}=q\,v\,B\] Potvrdite potvrdni okvir. Ako je naboj pozitivan, Lorentzova sila nije usmjerena prema središtu zadane kružnice.
Lorentzova sila ima ulogu centripetalne sile: \[\frac{m\,v^{2}}{r}=q\,v\,B\] Iz ovog izraza za brzinu dobijemo: \[v=\frac{q\,B\,r}{m}\qquad(1)\] Brzina kod jednolikog gibanja po kružnici možemo prikazati pomoću polumjera kružnice \(r\) i ophodnog vremena \(T\): \[v=\frac{2\,r\,\pi}{T}\qquad(2)\] Izjednačimo desne strane izraza (1) i (2): \[\frac{q\,B\,r}{m}=\frac{2\,r\,\pi}{T}\Rightarrow T=\frac{2\,\pi\,m}{q\,B}\] Negativno nabijena čestica se u magnetskom polju nalazi polovinu ophodnog vremena: \[\frac{T}{2}=\frac{\pi\,m}{q\,B}=1,77\cdot 10^{-11}\,\textrm{s}\]
35. zadatak
Učenici trebaju istražiti kako period titranja tijela ovješenoga o elastičnu oprugu ovisi o konstanti elastičnosti.
35.1. Učenici od ponuđenoga pribora trebaju odabrati što im je potrebno kako bi proveli mjerenje:- tijelo mase \(m\), pet elastičnih opruga konstanta elastičnosti \(k_{1}\), \(k_{2}\), \(k_{3}\), \(k_{4}\), i \(k_{5}\), stativni pribor i zaporni sat
- tijelo mase \(m\), elastična opruga konstante elastičnosti \(k\), stativni pribor i zaporni sat
- pet tijela masa \(m_{1}\), \(m_{2}\), \(m_{3}\), \(m_{4}\), i \(m_{5}\), elastična opruga konstante elastičnosti \(k\), stativni pribor i zaporni sat
- pet tijela masa \(m_{1}\), \(m_{2}\), \(m_{3}\), \(m_{4}\), i \(m_{5}\), nerastezljiva nit duljine \(\ell\), stativni pribor i zaporni sat
- tijelo mase \(m\), pet nerastezljivih niti duljine \(\ell_{1}\), \(\ell_{2}\), \(\ell_{3}\), \(\ell_{4}\), i \(\ell_{5}\), stativni pribor i zaporni sat
- tijelo mase \(m\), nerastezljiva nit duljine \(\ell\), stativni pribor i zaporni sat.
Redni broj potrebnog pribora:
35.2. Rezultati mjerenja prikazani su grafički.
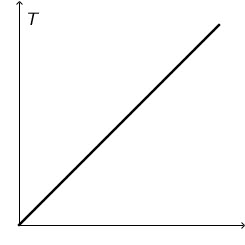
Koja se fizička veličina nalazi na osi apscise?
- A. \(k\)
- B. \(1/k\)
- C. \(\sqrt{k}\)
- D. \(1/\sqrt{k}\)
35.3. Kada u eksperimentu učenici zamijene prvu oprugu s drugom oprugom, frekvencija titranja poveća se dva puta.
Koliki je omjer između konstanta elastičnosti prve i druge opruge?
\(k_{1}/k_{2}\) =
35.1.
Želimo li istražiti ovisnost perioda titranja utega ovješenog na elastičnu oprugu o konstanti elastičnosti opruge, moramo odabrati opruge
koje imaju različite konstante elastičnosti. Redni broj potrebnog pribora je 1.
35.2.
Kliknite na aplet. Aplet prikazuje \(T,k\) graf (ovisnost perioda titranja o konstanti elastičnosti opruge). Period harmonijskog titranja tijela ovješenog na oprugu prikazujemo izrazom: \[T=2\,\pi\sqrt{\frac{m}{k}}\]
Prethodni izraz zapišimo u obliku: \[T=2\,\pi\,\sqrt{m}\,\frac{1}{\sqrt{k}}\] Iz ovog izraza zaključujemo da je period titranja obrnuto proporcionalan kvadratnom korijenu konstante elastičnosti jer je masa utega konstantna: \[T\sim \frac{1}{\sqrt{k}}\] Prema tome, na apscisi se nanosi \(1/\sqrt{k}\).
Za provjeru ovog zaključka kliknite na potvrdni okvir \(1/\sqrt{k}\,\textrm{graf}\). Taj graf je dio pravca, a tako je prikazano i u zadatku.
35.3.
Konstantu eleastičnosti opruge prikazujemo kao:
\[k=m\,\omega^{2}=m\,\left (2\,\pi\,f\right )^{2}=4\,m\,\pi^{2}\,f^{2}\]
\[\frac{k_{1}}{k_{2}}=\frac{4\,m\,\pi^{2}\,f_{1}^{\,2}}{4\,m\,\pi^{2}\,f_{2}^{\,2}}\]
\[\frac{k_{1}}{k_{2}}=\left (\frac{f_{1}}{f_{2}}\right )^{2}=\left (\frac{f_{1}}{2\,f_{1}}\right )^{2}=\frac{1}{4}\]