Unutrašnja energija
Polazeći od osnovnih postavki molekularno-kinetičke teorije:
- molekule svih tijela se gibaju
- molekule međusobno djeluju silama
možemo zaključiti da molekule svih tijela imaju kinetičku i potencijalnu energiju. Zbog ogromnog broja molekula, ne možemmo znati energiju svake pojedine molekule, nego, služeći se metodama statističke fizike, možemo saznati samo njihove srednje vrijednosti. No, zbog složenosti gibanja i molekularnih sila, i to nije uvijek moguće, osim kod idealnoga plina.
Zbroj srednje kinetičke i srednje potencijalne energije svih molekula nekoga tijela nazivamo njegovom unutrašnjom energijom:
$$U=N\overline{E}_{k}+N\overline{E}_{p}+...$$
Tu bi još trebalo dodati energiju atoma unutar molekula, energiju elektrona unutar atoma ...
Zbog svega toga nemoguće je napisati izraz za unutrašnju energiju nekoga tijela, osim u slučaju idealnoga plina. Međutim, promjenu unutrašnje energije nekoga tijela moguće je saznati mjerenjem makroskopskih veličina, poput temperature.
Unutrašnja energija idealnoga plina
U modelu idealnoga plina zanemarujemo sile između molekula, zbog čega je srednja potencijalna energija jednaka nuli: $N\overline{E}_{p}$, pa za unutrašnju energiju idealnoga plina dobijemo:
$$U=N\overline{E}_{k}$$
Srednju kinetičku energiju molekula jednoatomnoga idealnoga plina možemo prikazati kao:
$$\overline{E}_{k}=\frac{3}{2}kT$$
Prema tome, unutrašnja energija idealnoga plina jednaka je:
$$U=\frac{3}{2}NkT$$
Ako to povežemo s jednadžbom stanja idealnoga plina, dobivamo:
$$U=\frac{3}{2}PV$$
Temodinamička ravnoteža i toplina
Dva tijela različitih temperatura imaju različite unutrašnje energije, pri čemu će tijelo veće temperature imati i veću unutrašnju energiju. Neka su temperature dvaju tijela $T_{1}$ i $T_{2}$, a njihove unutrašnje energije $U_{1}$ i $U_{2}$, i neka je $T_{1} > T_{2}$. Tada je i $U_{1} > U_{2}$. Mase tijela su $m_{1}$ i $m_{2}$.
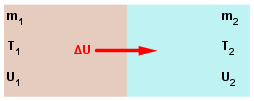
Unutrašnja energija prelazit će sa tijela više na tijelo niže temperature sve dok se one ne izjednače. Kažemo da je nastupila termodinamička (toplinska) ravnoteža.

Termodinamička ravnoteža je stanje kojega poprimaju dva tijela ako su bila dovoljno dugo u kontaktu. U stanju termodinamičke ravnoteže, oba tijela poprimaju jednaku temperaturu. U našem je primjeru $T_{1} > T > T_{2} $
Dio unutrašnje energije, $\Delta U$, koji je prešao sa tijela više na tijelo niže temperature nazivamo toplinom ili količinom topline. Toplinu označavamo s Q:
$$Q=\Delta U$$
Izmjena topline pri zagrijavanju i hlađenju
Označimo toplinu koju je toplije tijelo predalo s $Q_{1}$, a toplinu koju je hladnije tijelo primilo s $Q_{2}$. Zbog zakona sačuvanja energije vrijedi (ako tijela čine zatvoreni sustav):
$$Q_{1}=Q_{2}$$
Toplina koju su tijela razmijenila ovisi o vrsti materijala od kojega je tijelo napravljeno, masi tijela i promjeni temperature. Toplina koju je toplije tijelo predalo jednaka je:
$$Q_{1}=m_{1}c_{1}(T_{1}-T)$$
Toplina koju je hladnije tijelo primilo jednaka je:
$$Q_{2}=m_{2}c_{2}(T-T_{2})$$
Ovdje su $c_{1}$ i $c_{2}$ konstante ovisne o vrsti tijela. Tu konstantu nazivamo specifični toplinski kapacitet tijela.
Općenito, količina topline koju tijelo zagrijavanjem prima ili hlađenjem predaje, jednaka je:
$$Q=mc\Delta T$$
Sada možemo definirati specifični toplinski kapacitet:
$$c=\frac{Q}{m\Delta T}$$
Specifični toplinski kapacitet jednak je količini topline potrebnoj da se jednom kilogramu neke tvari temperatura poveća za jedan stupanj.
Jedinica za specifični toplinski kapacitet je:
$$\left [\, c \,\right ]=\frac{J}{kg\cdot K}$$
Promjena agregatnih stanja
Ukoliko se ne mijenja agregatno stanje tvari kojoj dovodimo toplinu, njezina će temperatura rasti. Prilikom promjene agregatnog stanja temperatura se ne mijenja sve dok se tijelo u čvrstom stanju potpuno ne rastali (taljenje), odnosno, dok tijelo u tekućem stanju potpuno ne ispari (isparavanje.)
Količinu topline pri kojoj se temperatura ne mijenja nazivamo latentnom toplinom.
Taljenje je proces prijelaza tvari iz čvrstoga u tekuće agregatno stanje. Temperaturu pri kojoj nastupa taljenje nazivamo talište. Latentna toplina taljenja je toplina koju treba dovesti tijelu da se ono potpuno rastali:
$$Q_{t}=\lambda m$$
Konstanta $\lambda$ ovisna je o vrsti tvari i nazivamo ju specifična toplina taljenja:
$$\lambda=\frac{Q_{t}}{m}$$
Specifična toplina taljenja jednaka je količini topline potrebnoj da se potpuno rastali jedan kilogram te tvari.
Jedinica za specifičnu toplinu taljenja je:
$$\left [\, \lambda \, \right ]=\frac{J}{kg}$$
Isparavanje je proces prijelaza tvari iz tekućega u plinovito agregatno stanje. Temperaturu pri kojoj nastupa isparavanje nazivamo vrelište. Latentna toplina isparavanja je toplina koju treba dovesti tijelu u tekućem stanju da ono potpuno ispari:
$$Q_{i}=r m$$
Konstanta $r$ ovisna je o vrsti tvari i nazivamo ju specifična toplina isparavanja:
$$r=\frac{Q_{i}}{m}$$
Specifična toplina isparavanja jednaka je količini topline potrebnoj da potpuno ispari jedan kilogram tvari u tekućem stanju.
Jedinica za specifičnu toplinu isparavanja je:
$$\left [\, r \, \right ]=\frac{J}{kg}$$
Prijelaz agregatnih stanja možemo pratiti na crtežu:
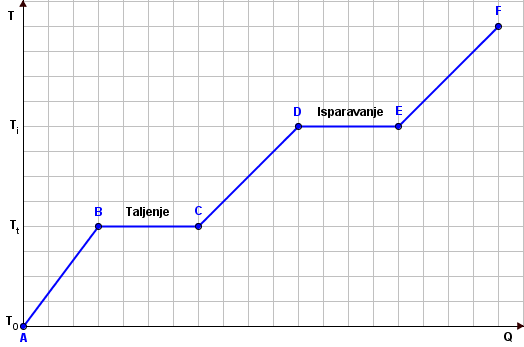
- A-B
Zagrijavanje tijela u čvrstom stanju. Tijelo prima toplinu $Q_{A-B}=mc(T_{t}-T_{0})$ i temperatura mu raste od početne $T_{0}$ do tališta $T_{t}$. - B-C
Dostignuta je temperatura tališta. Tijelo prima toplinu koja je jednaka latentnoj toplini taljenja $Q_{B-C}=\lambda m$ a temperatura ostaje ista sve dok se tijelo potpuno ne rastali. - C-D
Zagrijavanje tijela u tekućem stanju. Tijelo prima toplinu $Q_{C-D}=mc(T_{i}-T_{t})$ i temperatura mu raste od $T_{t}$ do vrelišta $T_{i}$. - D-E
Dostignuta je temperatura vrelišta. Tijelo prima toplinu koja je jednaka latentnoj toplini isparavanja $Q_{D-E}=r m$ a temperatura ostaje ista sve dok tvar potpuno ne ispari. - E-F
Zagrijavanje tijela u plinovitom stanju. Tijelo prima toplinu $Q_{E-F}=mc(T-T_{i})$ i temperatura mu raste od $T_{i}$ do neke temperature $T$.
Ako tijelo oslobađa toplinu u okolinu, događaju se obrnuti procesi
- Proces prijelaza plinovitoga u tekuće agregatno stanje naziva se kondenzacija. Pri tome se oslobađa latentna toplina isparavanja.
- Proces prijelaza tekućeg u čvrsto agregatno stanje naziva se očvršćivanje i pri tome se oslobađa latentna toplina taljenja.
- Pri ovim procesima temperature vrelišta i tališta ne mijenjaju se.
Toplinska vodljivost
Prijenos topline između tijela različitih temperatura vrši se na tri osnovna načina:
- Vođenjem ili kondukcijom toplina se prenosi kod čvrstih tijela. Dio tijela se grije neposrednim dodirom s izvorom topline, a susjedni dijelovi se postupno zagrijavaju. Najbolji vodič topline je srebro, a zatim ostali metali. Kako su dobri vodiči topline ujedno i dobri vodiči električne struje, vođenje se objašnjava gibanjem slobodnih elektrona.
- Strujanjem ili konvekcijom toplina se prenosi u tekućinama i plinovima. Strujanje nastaje zbog promjene gustoća uslijed zagrijavanja.
- Toplinskim zračenjem ili radijacijom. Radi se o elektromagnetskom zračenju svih tijela koja se nalaze na temperaturi iznad apsolutne nule. Toplina koju tijela zrače ovisi o temperaturi tijela i i njegovoj površini. Tijelo koje apsorbira zračenje, zagrijava se
Toplinski izolatori su tijela koja ne vode toplinu, ili ju jako slabo vode.