Ljetni rok 2018. godine
1. zadatak
Nakon vremena \(t\) tijelo prijeđe put koji je opisan izrazom \(s=3\,\textrm{m}+5\, \textrm{ms}^{-1}\, t\).
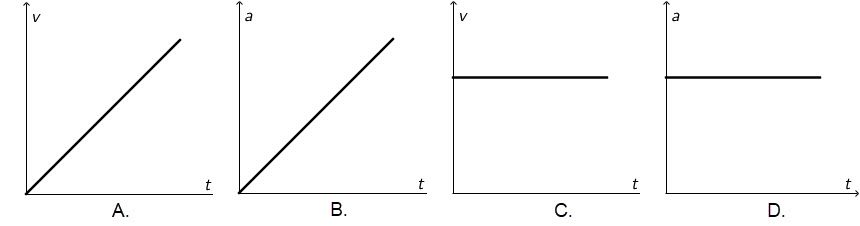
Koji od ponuđenih grafova opisuje gibanje toga tijela?
- A. Graf A.
- B. Graf B.
- C. Graf C.
- D. Graf D.
O kakvom se gibanju radi u ovom zadatku?
Put \[s=3\,\textrm{m}+5\, \textrm{ms}^{-1}\, t\] općenito prikazujemo jednadžbom \[s=s_{0}+v\,t\] To je jednadžba puta pri jednolikom gibanju po pravcu. Brzinu jednolikog pravocrtnog gibanja prikazuje graf C.
2. zadatak
Na slici su prikazana tri tijela različitih masa ovješena u točki E.
Mase tijela iznose \(m_{1}=1,5\, \textrm{kg},\ m_{2}=2\, \textrm{kg}\) i \(m_{3}=0,5\, \textrm{kg}\).
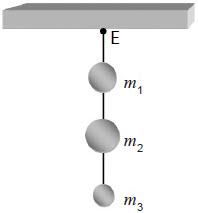
Kolika je napetost niti između tijela masa \(m_{1}\) i \(m_{2}\)?
- A. 5 N
- B. 15 N
- C. 25 N
- D. 40 N
Kolikom silom uteg mase \(m_{2}\) napinje nit?
Kolikom silom uteg mase \(m_{3}\) napinje nit?
Uteg mase \(m_{2}\) napinje nit silom \(m_{2}\textrm{g}=20\, \textrm{N}\), a uteg mase \(m_{3}\) silom \(m_{3}\textrm{g}=5\, \textrm{N}\). Napetost niti između tijela masa \(m_{1}\) i \(m_{2}\) iznosi 20 + 5 = 25 N.
3. zadatak
Dizalica stalnom brzinom podiže teret mase 2 t na visinu 4 m.
Koliki je uloženi rad dizalice ako je korisnost 40 %?
- A. 20 kJ
- B. 32 kJ
- C. 80 kJ
- D. 200 kJ
Odredite koristan rad.
Što je uloženi rad?
Kako je definirana korisnost?
Koristan rad je \(W_{\textrm{k}}=m\,g\,h=80\, 000\, \textrm{J}\). Iz korisnosti dizalice \[\eta=\frac{W_{\textrm{k}}}{W_{\textrm{u}}}\] odredimo uloženi rad: \[W_{\textrm{u}}=\frac{W_\textrm{k}}{\eta}=200\, 000\, \textrm{J}=200\, \textrm{kJ}\]
4. zadatak
Tijelo se nalazi u tekućini gustoće \(\rho\) tako da je 1/5 volumena tijela iznad površine tekućine.
Kolika je gustoća tijela?
- A. \(\rho/5\)
- B. \(\rho/2\)
- C. \(4\rho/5\)
- D. \(\rho\)
Koje sile djeluju na tijelo?
Što možemo zaključiti o iznosu i orijentaciji tih sila ako tijelo pluta na površini tekućine?
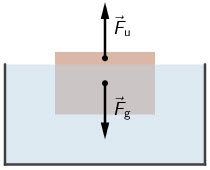
Tijelo pluta na površini tekućine. To znači da su uzgon i sila teža u ravnoteži: \[F_{\textrm{u}}=\rho\, g\cdot\frac{4}{5}V\] \[F_{\textrm{g}}=m\,g=\rho_{\textrm{tijela}}V\,g\] \[F_{\textrm{u}}=F_{\textrm{g}}\] \[\frac{4}{5}\rho\, g\,V=\rho_{\textrm{tijela}}\,V\,g\, \Rightarrow\rho_{\textrm{tijela}}=\frac{4}{5}\rho\]
5. zadatak
Tlak idealnoga plina poveća se izohorno za 15 %.
Koliko se poveća temperatura plina?
- A. 10 %
- B. 15 %
- C. 30 %
- D. 85 %
Primijenite jednadžbu za izohornu promjenu stanja plina.
Konačni tlak je za 15 % veći od početnog: \(p=1,15\, p_{0}\). Primijenimo jednadžbu izohorne promjene stanja plina: \[\frac{p_0}{T_0}=\frac{p}{T}\Rightarrow T=\frac{p\,T_{0}}{p_{0}}\] \[T=\frac{p\,T_{0}}{p_{0}}=\frac{1,15\,p_{0}\,T_{0}}{p_{0}}=1,15\,T_{0}\] \[\Delta T=T-T_{0}=1,15\,T_{0}-T_{0}=0,15\,T_{0}\] Temperatura plina povećala se za 15 % početne temperature.
6. zadatak
Na slici je prikazan kružni proces idealnoga plina u \(p,V\) grafu.
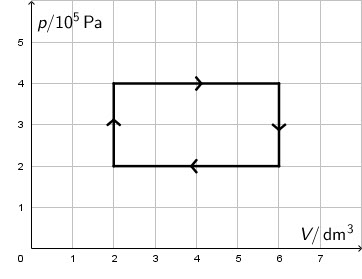
Koliki rad obavi idealni plin u kružnome procesu?
- A. 800 J
- B. 1200 J
- C. 1600 J
- D. 2400 J
Kako određujemo rad plina u kružnom procesu pomoću \(p,V\) grafa?
Rad plina u kružnom procesu jednak je površini pravokutnika u \(p, V\) grafu:
\[W=2\cdot{10}^5\cdot 4\cdot{10}^{-3}=800\, \textrm{J}\]
Napomena
Zbog neprecizno formuliranog zadatka na ocjenjivanju su priznavali A ili C kao točan odgovor.
7. zadatak
Kako se mijenjaju unutarnja energija \(\Delta U\), toplina \(Q\) i rad \(W\) u procesu adijabatske kompresije idealnoga plina?
- A. \(\Delta U > 0, Q = 0,\ W < 0\)
- B. \(\Delta U > 0, Q = 0,\ W > 0\)
- C. \(\Delta U = 0, Q < 0,\ W < 0\)
- D. \(\Delta U > 0, Q > 0,\ W > 0\)
U adijabatskom procesu nema izmjene topline između termodinamičkog sustava i okoline.
U adijabatskom procesu nema izmjene topline između plina i okoline. Ako se plin širi, unutarnja energija se smanjuje, a rad plina je pozitivan. Ako plin adijabatski sabijamo, unutarnja energija se povećava, a rad je negativan.
8. zadatak
Pločasti kondenzator s razmakom između ploča d spojen je na izvor napona. Kondenzator se zatim odvoji od izvora, a razmak između ploča se smanji.
Koja će se od navedenih fizičkih veličina smanjiti pri približavanju ploča kondenzatora?
- A. električno polje između ploča
- B. kapacitet kondenzatora
- C. naboj na pločama kondenzatora
- D. razlika potencijala između ploča
Koja se fizička veličina neće mijenjati nakon što kondenzator nabijemo i zatim ga odvojimo od izvora napona?
Ako kondenzator nabijemo i zatim ga odvojimo od izvora napona, naboj na pločama kondenzatora neće se mijenjati: \[q=\textrm{konst.}\] Smanjivanjem razmaka između ploča \(d\), njegov se kapacitet povećava: \[C=\varepsilon_{0}\,\varepsilon_{\textrm{r}}\frac{S}{d}\] To zbog \[q=C\,U\] znači da će se napon (razlika potencijala) smanjivati.
9. zadatak
Koliki je električni otpor bakrene žice duljine 100 km i poprečnoga presjeka \(20\,\textrm{mm}^{2}\)?
Električna otpornost bakra je \(0,0172\cdot 10^{-6}\, \Omega \textrm{m}\).
- A. \(0,000086\, \Omega\)
- B. \(0,086\, \Omega\)
- C. \(86\, \Omega\)
- D. \(86000\, \Omega\)
Kojim izrazom prikazujemo električni otpor vodiča?
\[R=\rho \frac{\ell}{S}=0,0172\cdot 10^{-6}\frac{10^{5}}{20\cdot 10^{-6}}=86\,\Omega\]
10. zadatak
Homogenu metalnu žicu otpora R razrežemo na četiri jednaka dijela koje zatim međusobno paralelno spojimo.
Koliki je ukupni otpor?
- A. R/16
- B. R/4
- C. R
- D. 4R
Koliki je otpor svakog dijela žice nakon što žicu razrežemo na četiri jednaka dijela?
Kada žicu razrežemo na četiri jednaka dijela, dobijemo četiri otpornika kojima su otpori R/4. Ukupni otpor paralelno spojenih otpornika jednak je: \[\frac{1}{R^{\prime}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}+\frac{1}{R_{4}}\] \[\frac{1}{R^{\prime}}=\frac{4}{R}+\frac{4}{R}+\frac{4}{R}+\frac{4}{R}=\frac{16}{R}\] \[R^{\prime}=\frac{R}{16}\]
11. zadatak
Koja od ponuđenih slika točno prikazuje silnicu magnetskoga polja oko ravnoga vodiča kojim prolazi struja okomito na ravninu papira?
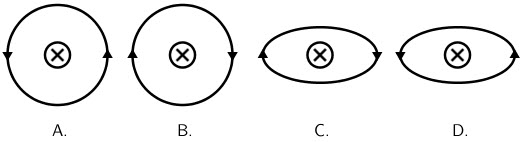
- A. Slika A.
- B. Slika B.
- C. Slika C.
- D. Slika D.
Primijenimo pravilo desne ruke.
Ako palac desne ruke postavimo u smjer struje, savijeni prsti će pokazivati smjer magnetskih silnica.
12. zadatak
Tijelo ovješeno na elastičnu oprugu harmonijski titra.
Koja je od navedenih tvrdnja točna za brzinu i akceleraciju tijela u amplitudnome položaju?
- A. Brzina i akceleracija su maksimalne.
- B. Brzina i akceleracija su nula.
- C. Brzina je maksimalna, a akceleracija je nula.
- D. Brzina je nula, a akceleracija je maksimalna.
- Kolika je harmonijska sila u amplitudnom, a kolika je u ravnotežnom položaju?
- Kolika je brzina u amplitudnom, a kolika je u ravnotežnom položajuU
U amplitudnom položaju tijelo za trenutak zastane pa je brzina jednaka nuli, dok je harmonijska sila \[\left |\vec{F}\right |=k\,x\] maksimalna. Maksimalna sila, na osnovu temeljnog zakona gibanja: \[a=\frac{F}{m}\] prouzrokovat će maksimalnu akceleraciju.
13. zadatak
Na slici je prikazano matematičko njihalo koje se sastoji od tijela mase \(m\) i nerastezljive niti duljine \(\ell\). Njihalo harmonijski titra oko ravnotežnoga položaja F i postiže amplitudni položaj u točki E.
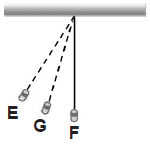
Koja je od navedenih tvrdnja o kinetičkoj energiji njihala točna?
- A. Njihalo ima najveću kinetičku energiju u položaju E.
- B. Njihalo ima najveću kinetičku energiju u položaju G.
- C. Njihalo ima najveću kinetičku energiju u položaju F.
- D. Njihalo ima jednaku kinetičku energiju u položajima E, F i G.
Elastična potencijalna energija najveća je u amplitudnom položaju, a najmanja (jednaka nuli) u ravnotežnom položaju.
Kinetička energija njihala najveća je u ravnotežnom položaju, a najmanja u amplitudnom položaju.
14. zadatak
Na slici je prikazan spektar elektromagnetskih valova po valnim duljinama.
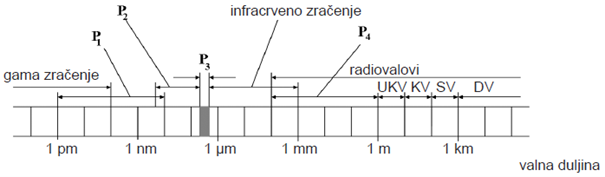
U kojemu se dijelu spektra označenoga s \(P_{1}\), \(P_{2}\), \(P_{3}\) ili \(P_{4}\) nalaze mikrovalovi?
- A. \(P_{1}\)
- B. \(P_{2}\)
- C. \(P_{3}\)
- D. \(P_{4}\)
Mikrovalovi su elektromagnetski valovi valnih duljina između 1 mm i 1 m.
Mikrovalovi su elektromagnetski valovi valnih duljina između 1 mm i 1 m.
15. zadatak
Hitna pomoć projuri pokraj mirnoga opažatelja s uključenom zvučnom sirenom.
Koja je od navedenih tvrdnja točna za frekvenciju zvuka koju čuje opažatelj?
- A. Veća je kad se hitna pomoć približava, a manja kad se udaljava.
- B. Manja je kad se hitna pomoć približava, a veća kad se udaljava.
- C. Veća je kada se hitna pomoć približava i udaljava.
- D. Ne mijenja se kada se hitna pomoć približava i udaljava.
Pomoć potražite na poveznici Dopplerov učinak
Frekvencija zvuka koju čuje slušatelj može biti veća ili manja od frekvencije zvuka koju emitira izvor zvuka.
\[f_{\textrm{s}}=f_{\textrm{i}}\thinspace\frac{v}{v-v_{\textrm{s}}}\]
Kada se izvor zvuka približuje, \(v_{\textrm{i}} > 0\) pa je nazivnik manji od brojnika, zbog čega je \(f_{\textrm{s}} > f_{\textrm{i}}\).
Kada se izvor zvuka udaljuje, \(v_{\textrm{i}}< 0\) pa je nazivnik veći od brojnika, zbog čega je \(f_{\textrm{s}} < f_{\textrm{i}}\).
16. zadatak
Predmet se nalazi na udaljenosti od konveksnoga zrcala koja je jednaka radijusu zakrivljenosti zrcala.
Kakva je slika nastala?
- A. realna i obrnuta
- B. realna i uspravna
- C. virtualna i uspravna
- D. virtualna i obrnuta
Pomoć potražite na poveznici Konveksno zrcalo
Konveksno zrcalo uvijek daje virtualnu, uspravnu i umanjenu sliku.
17. zadatak
Učenik je izveo eksperiment u kojemu je laserski snop svjetlosti usmjerio na tanku vlas kose i promatrao nastalu sliku na zastoru.
Koja se fizička pojava može dokazati tim eksperimentom?
- A. polarizacija svjetlosti
- B. fotoelektrični učinak
- C. disperzija svjetlosti
- D. ogib svjetlosti
Ogib ili difrakcija je pojava širenja valova iza prepreke ili pukotine na koju naiđu.
Ogib ili difrakcija je pojava širenja valova (laserska svjetlost je također val) iza prepreke (nit u ovom primjeru) ili pukotine na koju naiđu.
18. zadatak
Kolika je energija \(E_{0}\) mirovanja elektrona?
- A. 0,0017 eV
- B. 0,512 eV
- C. 0,0017 MeV
- D. 0,512 MeV
Energija mirovanja: \[E_{0}=mc^{2}\]
\[E_{0}=mc^{2}=9,11\cdot{10}^{-31}\cdot\left(3\cdot{10}^8\right)^{2}\] \[E_{0}=8,2\cdot{10}^{-14}\, \textrm{J}=0,512\, \textrm{MeV}\]
19. zadatak
Na slici su prikazane energijske razine atoma nekoga elementa. Elektron prelazi iz energijskoga stanja \(E_{4}\) u stanje \(E_{1}\), pri čemu su svi prijelazi između razina dopušteni.
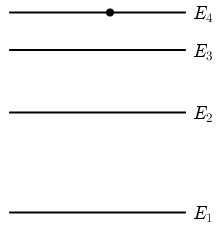
Koliko različitih fotona s obzirom na valnu duljinu atom može pritom emitirati?
- A. 3
- B. 4
- C. 5
- D. 6
\(E_{4}\rightarrow\ E_{3}\), \(E_{3}\rightarrow\ E_{2}\), \(E_{2}\rightarrow\ E_{1}\), \(E_{4}\rightarrow\ E_{2}\),\(E_{4}\rightarrow\ E_{1}\),
\(E_{3}\rightarrow\ E_{1}\)
Ukupno šest fotona različitih energija.
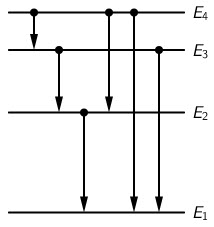
\(E_{4}\rightarrow\ E_{3}\), \(E_{3}\rightarrow\ E_{2}\), \(E_{2}\rightarrow\ E_{1}\), \(E_{4}\rightarrow\ E_{2}\),\(E_{4}\rightarrow\ E_{1}\),
\(E_{3}\rightarrow\ E_{1}\)
Ukupno šest fotona različitih energija.
20. zadatak
Što se emitira pri gama raspadu?
- A. jezgre helija
- B. brzi elektroni
- C. pozitroni
- D. elektromagnetski valovi
Pomoć potražite na poveznici Gama-radioaktivnost
Pri gama-raspadu emitiraju se elektromagnetski valovi.
21. zadatak
Tijelo G bačeno je vertikalno prema gore s visine \(h\) početnom brzinom iznosa \(v_{\small\textrm{G}}\). Tijelo H bačeno je
vertikalno prema dolje s iste visine \(h\) početnom brzinom iznosa \(v_{\small\textrm{H}}\).
Što vrijedi za brzine kojima tijela padnu na tlo ako su početne brzine \(v_{\small\textrm{G}}\) i \(v_{\small\textrm{H}}\) jednakoga iznosa?
Zanemarite otpor zraka.
- A. Brzina tijela G veća je od brzine tijela H.
- B. Brzina tijela G manja je od brzine tijela H.
- C. Brzina tijela G jednaka je brzini tijela H.
Primijenite zakon očuvanja mehaničke energije.
Ukupna mehanička energija tijela G u trenutku izbacivanja: \[E_{\small\textrm{G}}=m\,g\,h+\frac{m\,{v_{\small\textrm{G}}^2}}{2}\] Ukupna mehanička energija tijela H u trenutku izbacivanja: \[E_{\small\textrm{H}}=m\,g\,h+\frac{m\,{v_{\small\textrm{H}}^2}}{2}\] Prema zakonu očuvanja mehaničke energije (otpor zraka je zanemaren): \[E_{\small\textrm{G}}=E_{\small\textrm{H}}\] \[m\,g\,h+\frac{m\,{v_{\small\textrm{G}}^2}}{2}=m\,g\,h+\frac{m\,{v_{\small\textrm{H}}^2}}{2}\Rightarrow v_{\small\textrm{G}}^{2}=v_{\small\textrm{H}}^{2}\] \[v_{\small\textrm{G}}^{\,}=v_{\small\textrm{H}}^{\,}\]
22. zadatak
Na slici su prikazana dva planeta D i E mase \(m\) i planet F mase \(4\,m\). Središta planeta nalaze se na istome pravcu, a udaljenost između središta dvaju susjednih planeta je \(d\).
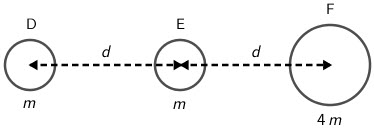
Između kojih planeta gravitacijska sila ima najveći iznos?
- A. D i E
- B. D i F
- C. E i F
Primijenite Newtonov zakon gravitacije.
Sila između planeta D i E: \[F_{\small{\textrm{DE}}}=G\frac{m^2}{d^2}\] Sila između planeta E i F: \[F_{\small{\textrm{EF}}}=G\frac{4\,m^2}{d^2}\] Sila između planeta D i F: \[F_{\small{\textrm{DF}}}=G\frac{4\,m^2}{\left (2\,d\right )^2}=G\frac{m^2}{d^2}\] Iz prethodna tri izraza vidimo da je sila između planeta E i F najveća: \[F_{\small{\textrm{EF}}} > F_{\small{\textrm{DE}}}=F_{\small{\textrm{DF}}}\]
23. zadatak
Aluminij, željezo i voda imaju jednaki volumen pri temperaturi \(20\,^{0}\textrm{C}\).
Koja će tvar imati najveći volumen ako se sve tvari zagriju na jednaku temperaturu od \(80\,^{0}\textrm{C}\).
Za volumne koeficijente rastezanja
\(\alpha\) vrijedi \(\alpha_{\textrm{Al}} < \alpha_{\textrm{Fe}} < \alpha_{\textrm{voda}}\).
- A. Aluminij
- B. Voda
- C. Željezo
Pomoć potražite na poveznici Volumno toplinsko širenje.
Volumno toplinsko širenje: \[V=V_{0}\left(1+\alpha\Delta t\right)\] Aluminij, željezo i voda imaju jednak volumen \(V_{0}\) pri istoj početmoj temperaturi. Pri porastu temperature za jednak iznos \(\Delta t\) najviše će se volumno proširiti tvar koja ima najveći volumni koeficijent rastezanja, a to je voda.
24. zadatak
Učenik izvodi eksperiment tako da metalnoj neutralnoj kugli približi negativno nabijeni plastični štap pazeći da ne dotakne kuglu. Zatim dok je negativni štap
i dalje u blizini kugle, negativno nabijenu stranu kugle kratko uzemlji.
Kako će biti nabijena kugla ako se nakon toga prvo prekine uzemljenje, a zatim udalji negativno nabijeni štap?
- A. Bit će negativno nabijena.
- B. Bit će pozitivno nabijena.
- C. Ostat će neutralna.
Pomoć potražite na poveznici Elektrizacija tijela.
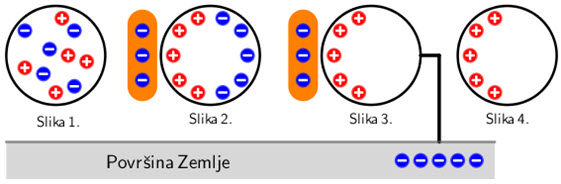
-
Slika 1.
Neutralna kugla ima jednak iznos pozitivnog i negativnog naboja. -
Slika 2.
Neutralnoj kugli približimo negativno nabijeni štap, pri čemu dolazi do razdvajanja naboja na kugli. Pozitivni naboji približit će se štapu, a negativni udaljiti. -
Slika 3.
Stranu kugle koja je negativno nabijena uzemljimo. Elektroni s kugle prelaze u površinu Zemlje. -
Slika 4.
Nakon što prekinemo uzemljenje i negativno nabijeni štap udaljimo od kugle, kugla ostaje pozitivno nabijena.
25. zadatak
Na grafu je prikazana ovisnost kapacitivnoga otpora \(R_{\small\textrm{C}}\) o periodu \(T\) izmjenične struje za kondenzatore kapaciteta \(C_{1}\) i \(C_{2}\).
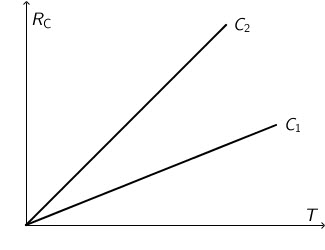
Koji je odnos kapaciteta \(C_{1}\) i \(C_{2}\)?
- A. \(C_{1} > C_{2}\)
- B. \(C_{1} < C_{2}\)
- C. \(C_{1} = C_{2}\)
Pomoć potražite na poveznici Kapacitivni otpor.
U izraz za kapacitivni otpor \[R_{\small\textrm{C}}=\frac{1}{C\,\omega}\] uvrstimo \[\omega=\frac{2\pi}{T}\] \[R_{\small\textrm{C}}=\frac{1}{C}\cdot\frac{T}{2\,\pi}=\frac{1}{2\pi C}\cdot T\] Koeficijent smjera pravca je \[\frac{1}{2\pi C}\ \] Iz grafa vidimo da veći koeficijent smjera pa prema tome i manji kapacitet ima kondenzator kapaciteta \(C_{2}\).
26. zadatak
Mjesec obiđe Zemlju 13 puta u godini.
Kolika je kutna brzina kojom Mjesec kruži oko Zemlje? Godina ima 365 dana.
Odgovor: rad/s
Pomoć potražite na poveznici: Jednoliko kružno gibanje.
Ophodno vrijeme (period) Mjeseca oko Zemlje: \[T=\frac{365\cdot 24\cdot 3600}{13}=2,43\cdot 10^{6}\, \textrm{s}\] Kutna brzina: \[\omega=\frac{2\,\pi}{T}=2,59\cdot 10^{-6}\, \frac{\textrm{rad}}{\textrm{s}}\]
27. zadatak
Korisnost toplinskoga stroja iznosi 20 %. Radno tijelo predaje određenu količinu topline spremniku temperature
300 K.
Kolika je temperatura spremnika od kojega radno tijelo prima toplinu?
Odgovor: K
Korisnost bilo kojeg toplinskog stroja definira se kao: \[\eta=1-\frac{|Q_{2}|}{Q_{1}}\]
- \(Q_{1}\) - toplina koju stroj prima od toplijeg spremnika.
- \(Q_{2}\) - toplina koju stroj predaje hladnijem spremniku.
Napomena
U tekstu zadatka nije napisano da se radi o Carnotovom stroju.
\[\eta=\frac{Q_{1}-Q_{2}}{Q_{1}}=1-\frac{Q_{2}}{Q_{1}}=1-\frac{T_{2}}{T_{1}}\]
\[T_1=\frac{T_{2}}{1-\eta}=\frac{300}{1-0,2}=375\, \textrm{K}\]
28. zadatak
U serijskome RLC spoju izmjenične struje induktivni otpor iznosi \(20\,\mathrm{\Omega}\), kapacitivni otpor \(60\,\mathrm{\Omega}\), a omski otpor
\(30\, \mathrm{\Omega}\).
Kolika je impedancija toga spoja?
Odgovor: \(\Omega\)
Pomoć potražite na poveznici: Serijski RCL krug.
Impedancija (ukupni otpor u krugu izmjenične struje): \[Z=\sqrt{R^2+\left(R_{\small\textrm{L}}-R_{\small\textrm{C}}\right)^2}=50\,\Omega\]
29. zadatak
Kolika je duljina matematičkoga njihala čiji je period titranja 2 s?
Odgovor: m
Pomoć potražite na poveznici: Titranje matematičkog njihala.
Iz izraza za period matematičkog njihala \[T=2\,\pi\sqrt{\frac{\ell}{g}}\] odredimo duljinu njihala: \[\ell=\frac{g\,T^{2}}{4\,\pi^{2}}=1,01\, \textrm{m}\]
30. zadatak
Koliko neutrona ima izotop \(\textrm{X}\) koji nastaje pri beta-minus raspadu izotopa \({_{\,\,88}^{228}}\,\textrm{Ra}\)?
Napišite jednadžbu toga beta-minus raspada.
Broj neutrona:
Pomoć potražite na poveznici: Beta-radioaktivnost.
Beta-minus raspad: \[{_{\,\,88}^{228}}\,\textrm{Ra}\rightarrow{_{-1}^{\,\,\,0}}\,\textrm{e}+{_{\,\,89}^{228}}\,\textrm{X}\]
- Broj nukleona: 228
- Broj protona = 89
- Broj neutrona = 228 - 89 = 139
31. zadatak
Kroz uži dio horizontalno položene cijevi polumjera 1 cm teče voda brzinom 2 m/s pri statičkome
tlaku 2·105 Pa.
Koliki je statički tlak u širemu dijelu te cijevi polumjera 1,73 cm? Gustoća vode je
1000 kg/m3.
Odgovor: Pa
Pomoć potražite na poveznicama:
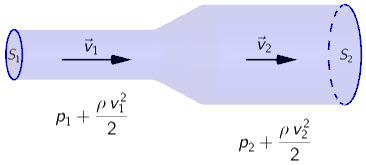
- \(S_{1}\) - površina poprečnog presjeka užeg dijela cijevi
- \(S_{2}\) - površina poprečnog presjeka šireg dijela cijevi
- \(v_{1}\) - brzina fluida u užem dijelu cijevi
- \(v_{2}\) - brzina fluida u širem dijelu cijevi
- \(p_{1}\) - statički tlak u užem dijelu cijevi
- \(p_{2}\) - statički tlak u širem dijelu cijevi
- \(\rho\) - gustoća fluida
- \(\Large{\frac{\rho\,v_{1}^{2}}{2}}\) - dinamički tlak u užem dijelu cijevi
- \(\Large\frac{\rho\,v_{2}^{2}}{2}\) - dinamički tlak u širem dijelu cijevi
Jednadžba kontinuiteta \[S_{1}\,v_{1}=S_{2}\,v_{2}\] Bernoullijeva jednadžba \[p_{1}+\frac{\rho\,v_{1}^{2}}{2}=p_{2}+\frac{\rho\,v_{2}^{2}}{2}\] Brzinu u širem dijelu cijevi odredimo pomoću jednadžbe kontinuiteta: \[v_2=\frac{S_1}{S_2}v_1\] \[v_{2}=\left(\frac{d_{1}}{d_{2}}\right)^{2}\cdot\ v_{1}=0,67\, \frac{\textrm{m}}{\textrm{s}}\] Primjenom Bernoullijeve jednadžbe odredimo statički tlak u širem dijelu cijevi: \[p_{2}=p_{1}+\frac{\rho}{2}\left(v_{1}^{2}-v_{2}^{2}\right)=201777\, \textrm{Pa}\]
32. zadatak
Koliku snagu mora imati grijač kako bi 250 g vode temperature \(100\,^0\textrm{C}\) isparilo za 1 h
ako se sva energija grijača upotrebljava za zagrijavanje vode?
Specifična toplina isparavanja vode je 2,26 MJ/kg.
Odgovor: W
Primijenite zakon očuvanja energije.
Toplina isparavanja: \[Q=m\,r\] Snaga grijača: \[P=\frac{Q}{t}=\frac{m\,r}{t}=156,94\, \textrm{W}\]
33. zadatak
Koliki je naboj kuglice mase 1 g koja lebdi u vakuumu iznad druge kuglice s nabojem 7,04·10^{-9} C na udaljenosti 5 cm
Odgovor: C
Kuglica će lebdjeti ako je rezultanta svih sila koje na nju djeluju jednaka nuli. Koje sile djeluju na kuglicu mase 1 g?
Jesu li kuglice nabijene nabojem jednakog ili suprotnog predznaka?
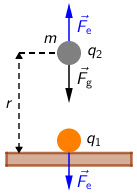
Odbojna električna sila na kuglicu mase 1 g i sila teža koja na nju djeluje moraju biti jednake po iznosu i suprotno orijentirane: \[F_{e}=F_{\textrm{g}}\] \[k\frac{q_{1}\,q_{2}}{r^{2}}=m\,g\] \[q_{2}=\frac{m\,g\,r^2}{k\,q_{1}}=3,95\cdot 10^{-7}\, \textrm{C}\]
34. zadatak
Projektil mase 50 g leti brzinom 500 m/s i probije zid debljine 5 cm te se
nastavi gibati dalje brzinom 200 m/s.
Kolika je sila otpora zida? Pretpostavite da je sila otpora zida stalna.
Odgovor: N
Rad kojega obavi projektil da bi probio zid jednak je promjeni kinetičke energije projektila nakon i prije probijanja zida.
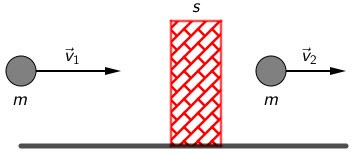
\[W=E_{\textrm{k}2}-E_{\textrm{k}1}\] \[W=\frac{mv_{2}^{2}}{2}-\frac{mv_{1}^{2}}{2}=\frac{m}{2}\left(v_{2}^{2}-v_{1}^{2}\right)=-5250\, \textrm{J}\] \[W=F\cdot s\Rightarrow F=\frac{W}{s}=-105000\, \textrm{N}\]
35. zadatak
Metalni obruč otpora \(2\, \mathrm{\Omega}\) nalazi se u homogenome magnetskom polju. Obruč je postavljen okomito na magnetske silnice.
Kolika količina naboja proteče obručem kada se magnetski tok promijeni za \(5\cdot 10^{-4}\, \textrm{Wb}\)?
Odgovor: C
Primijenite Faradayev zakon elektromagnetske indukcije.
Prema Faradayevom zakonu elektromagnetske indukcije, u obruču koji se nalazi u promjenjivom magnetskom polju inducira se elektromotorni napon:
\[U_{\textrm{i}}=-\frac{\Delta\phi}{\Delta t}\]
Za vrijeme \(\Delta t\) kroz obruč protekne naboj:
\[q=I\cdot\Delta t\]
Induciranu struju odredimo primjenom Ohmovog zakona:
\[I=\frac{U_{\textrm{i}}}{R}\]
\[q=I\cdot\Delta t=\frac{U_{\textrm{i}}}{R}\Delta t=-\frac{\Delta\phi}{\Delta t}\cdot\frac{\Delta t}{R}=-\frac{\Delta\phi}{R}=-2,5\cdot 10^{-4}\, \textrm{C}\]
Napomena
U ključu za odgovore koji je dao NCVVO količina naboja je pozitivna, što također može biti točno jer u zadatku ne piše je li se magnetski tok smanjio
ili povećao.
36. zadatak
Realna slika koja se dobije uz pomoć konkavnoga sfernog zrcala tri je puta veća od predmeta.
Kolika je žarišna daljina upotrijebljenoga zrcala ako su predmet i realna slika međusobno udaljeni 80 cm?
Odgovor: cm
Pomoć potražite na poveznici Konkavno zrcalo.
Linearno povećanje zrcala: \[m=-\frac{b}{a}\] Realna slika koju daje konkavno zrcalo je obrnuta pa je linearno povećanje negativno: \[m=-3\] Iz ova dva izraza dobijemo: \[b=3\,a\] U zadatku je zadana udaljenost između slike i predmeta: \[b-a=80\, \textrm{cm}\] Udaljenost predmeta od zrcala je \(a=40\, \textrm{cm}\) pa je slika udaljena: \[b=120\, \textrm{cm}\] U jednadžbu konkavnog zrcala: \[\frac{1}{a}+\frac{1}{b}=\frac{1}{f}\] uvrstimo \(a\) i \(b\). Za žarišnu udaljenost dobijemo: \[f=30\, \textrm{cm}\]
37. zadatak
Jedna banana prosječno sadržava 400 mg kalija od čega je 0,0117 % radioaktivni izotop \({_{19}^{40}}\, \textrm{K}\).
Vrijeme poluraspada toga izotopa je 4,027·1016 s, a molarna masa
39,96 g/mol.
Kolika je aktivnost u bekerelima radioaktivnoga uzorka iz jedne banane?
Odgovor: Bq
Pomoć potražite na poveznici Zakon radioaktivnog raspada.
Masa radioaktivnog kalija u jednoj banani je: \[m=1,17\cdot 10^{-4}\cdot 400 \cdot10^{-6}\, \textrm{kg}=4,68\cdot 10^{-8}\, \textrm{kg}\] Broj atoma u toj masi radioaktivnog kalija iznosi: \[N=\frac{m}{M}N_{\textrm{A}}=7,054\cdot 10^{17}\] Aktivnost uzorka jednaka je: \[A=\lambda N\] Odredimo konstantu radioaktivnog raspada kalija: \[\lambda=\frac{\textrm{ln}\,2}{T}=1,72\cdot 10^{-17}\, \textrm{s}^{-1}\] Za aktivnost dobijemo: \[A=12,14\, \textrm{Bq}\]