Stefan - Boltzmannov zakon
Ukupna energija zračenja koju apsolutno crno tijelo emitira u jednoj sekundi, ili ukupna snaga zračenja jednaka je:
$$P=\sigma ST^{4}$$
Ovdje je S površina crnoga tijela, a T apsolutna temperatura. Konstanta σ određena je mjerenjem i naziva se Stefan-Boltzmannova konstanta:
$$\sigma=5.67\cdot 10^{-8}\: Wm^{-2}K^{-4}$$
Do ovog zakona došao je Stefan eksperimentalno a Boltzmann ga je izveo u okviru termodinamike. Međutim, u tom se izvodu nije mogla odrediti konstanta.
Intenzitet zračenja definiramo kao:
$$\frac{E}{St}=\frac{P}{S}=\sigma T^{4}$$
Applet: Stefan - Boltzmannov zakon
Sljedeća animacija omogućava vam da vidite kako kako izgleda graf snage kao funkcija temperature i površine iz koje izlazi zračenje.
Za fino podešavanje klizača S i T, kliknite na točku na klizači i zatim koristite tipke + i - na vašoj tipkovnici.
Nedeljko Begović, kreirano programom GeoGebra
Pitanja i zadaci
- Pomičući klizač S mijenjate površinu crnoga tijela koja zrači. Kako se pri tome mijenja graf snage?
- Izaberite neku temperaturu, npr. 500 K i pročitajte snagu. Zatim, ne mijenjajući temperaturu, povećajte površinu dva puta. Što zaključujete?
- Izaberite neku površinu i više ju ne mijenjajte. Pročitajte snagu pri 5000 K i pri 10000 K. Što zaključujete?
- Možete li pomoću podataka prikazanih na grafikonu (S, T, P) odrediti intenzitet zračenja? Kako?
- Koliki je intenzitet zračenja crnoga tijela u obliku ploče površine 0.02 m2 pri temperaturi 5700 K? Smijete koristiti samo podatke koje vidite na grafikonu.
Wienov zakon
Wien je otkrio da je frekvencija kojoj odgovara maksimalna gustoća energije zračenja crnoga tijela to veća, što je temperatura veća.
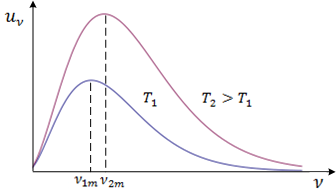
Ovo možemo zapisati ovako:
$$\nu _{max}=1.03\cdot 10^{11}T$$
Temperatura je u Kelvinima, a frekvencija u Hz.
Fizičari više vole izraziti ovisnost valne duljine zračenja crnog tijela, pri kojoj je intenzitet tog zračenja maksimalan, o temperaturi:
$$\lambda _{max}=\frac{b}{T}$$
Konstanta b je Wienova konstanta i iznosi:
$$b=2.89\cdot 10^{-3}mK$$
Applet: Wienov zakon
Sljedeća animacija omogućava vam da vidite kako kako izgleda graf valne duljine, pri kojoj je intenzitet zračenja najveći, u ovisnosti o temperaturi.
Za fino podešavanje klizača T kliknite na točku na klizači i zatim koristite tipke + i - na vašoj tipkovnici.
Pitanja i zadaci
- Kliknite na potvrdni okvir pokaži točku kako biste vidjeli položaj točke na grafu.
- Pomicanjem klizača T možete vidjeti kako se mijenja valna duljina za koju je intenzitet zračenja u spektru zračenja crnoga tijela najveći.
- Zapišite vrijednosti valnih duljina za nekoliko različitih temperatura i nakon toga provjerite rezultate računski.
Planckov zakon zračenja
Tijela zrače elektromagnetske valove zbog titranja električnih naboja. Titranje možemo opisati harmonijskim oscilatorom.
Prema klasičnoj teoriji, srednja energija harmonijskog oscilatora je jednaka: <E> = kT i prema tome, budući da se crno tijelo može nalaziti pri bilo kojoj temperaturi iznad apsolutne nule, energija može poprimiti i bilo koju vrijednost. Kažemo da se energija harmonijskog oscilatora može mijenjati kontinuirano.
Kako bi objasnio zakone zračenja crnog tijela, Planck je pretpostavio da harmonijski oscilator ne može poprimiti bilo koju energiju, nego se ona može mijenjati u skokovima ili kvantima, pri čemu svaki kvant ima energiju:
$$ E=h\nu$$
Ovdje je h Planckova konstanta:
$$h=6.626\cdot 10^{-34}Js$$
Energiju kvanta možemo prikazati i preko valne duljine emitiranog zračenja:
$$E=h\frac{c}{\lambda }$$
Prema tome, harmonijski oscilator može poprimiti energije:
$$ h\nu ,\: 2h\nu ,\: 3h\nu ,\: .......$$
ili, općenito:
$$E_{n}=nh\nu$$
Ovdje je n pozitibni cijeli broj.
Funkciju spektralne raspodjele češće prikazujemo kao funkciju valne duljine:
$$u_{\lambda }=\frac{8\pi hc}{\lambda^{5}}\frac{1 }{e^{hc/\lambda kT}-1}$$
Graf ove funkcije, za danu temperaturu, izgleda ovako:
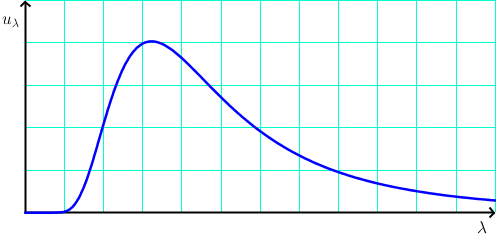
Na sljedećoj slici vidimo graf spektralne gustoće energije po valnim duljinama za nekoliko različitih temperatura:
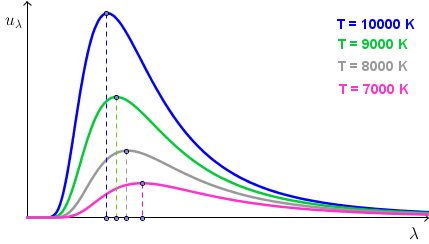
Primijetite kako se maksimalna energija zračenja pomiče prema manjim valnim duljinama sa porastom temperature (Wienov zakon).
Applet: Planckov zakon zračenja crnoga tijela
Sljedeća animacija omogućava vam da vidite kako kako izgleda ovisnost spektralne gustoće energije o valnoj duljini, s temperaturom kao parametrom
Za fino podešavanje klizača T kliknite na točku na klizači i zatim koristite tipke + i - na vašoj tipkovnici.
Fotoelektrični efekt
Ako na metal pada svjetlost (općenito, elektromagnetsko zračenje), slobodni elektroni u metalu dobiju dodatnu energiju koja može biti dovoljna da ih izbaci iz metala. Tu pojavu nazivamo fotoefekt (fotoelektrični učinak, fotoelektrični efek
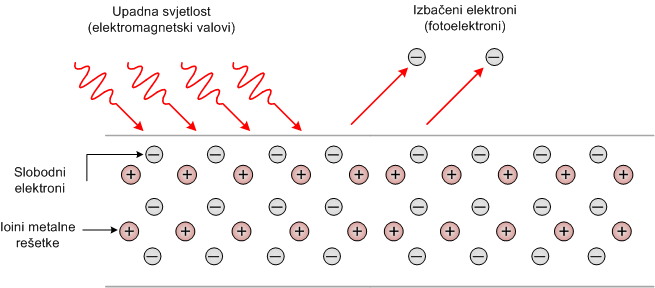
Energija vezanja
Slobodni elektroni u blizini površine metala imaju određenu energiju kojom su vezani za metal. Tu energiju nazivamo energija vezanja. Da bi slobodni elektroni mogli napustiti metal, potrebno im je dovesti dodatnu energiju koja je veća od energije vezanja. Tada elektron svladava privlačnu električnu silu kojom je vezan za metal i napušta ga. Pri tome se izvrši rad kojega nazivamo izlaznim radom i označavamo ga sa W0 Izlazni rad je jednak energiji vezanja.
Izlazni rad, odnosno energija vezanja, nejčešće se mjere u elektronvoltima. Elektronvolt (eV) jednak je radu što ga izvrši električno polje pri pomicanju elektrona između dvije točke između kojih je napon 1 V. Kada rješavamo zadatke, najčešće je potrebno elektronvolte pretvoriti u džule: 1 eV = 1.6·10-19 J.Einsteinovo objašnjenje fotoefekta
Einstein je 1905. godine predložio teoriju koja je objašnjavala sve eksperimentalne činjenice o fotoefektu. Radi se o vrlo jednostavnoj i elegantnoj teoriji, za koju je kasnije dobio i Nobelovu nagradu. Einstein je proširio Planckovu hipotezu o kvantima. Svako elektromagnetsko zračenje postoji u obliku diskretnih "paketa" elektromagnetske energije, koje nazivamo kvantima ili fotonima . Pri međudjelovanju sa tvari, foton se ponaša slično čestici i predaje svoju energiju pojedinim elektronima (ne tvari u cjelini, ne atomu u cjelini). Prema Plancku, energija jednog kvanta jednaka hν. Prema Einsteinu, ovo vrijedi i za fotone:$$E_{f}=h\nu$$
Kada foton padne na metal, ako pogodi elektron, predjae mu svoju energiju. Dio te energije troši se na svladavanje energije vezanja, W0, a dio na kinetičku energiju fotoelektrona:
$$E_{f}=W_{0}+E_{k}$$
Prema tome, kinetička energija fotoelektrona jednaka je:
$$E_{k}=h\nu -W_{0}$$
Sada možemo objasniti sve eksperimentalne činjenice fotoefekta.
Ukoliko foton ne "pogodi" elektron, nema emitiranih elektrona, ako ga pogodi, do fotoefekta može doći. Prema tome, vjerojatnost pogotka bit će to veća što je veći broj fotona, odnosno, što je veći intenzitet upadnog zračenja, jer je intenzitet zračenja koje pada na metal proporcionalan broju fotona:
$$I=\frac{E}{St}=\frac{NE_{f}}{St}$$
Analizirajmo sada jednadžbu:
$$E_{k}=h\nu -W_{0}$$
Fotoefekt se počinje opažati kada je energija fotona upravo jednaka energiji vezanja i tada je kinetička energija fotoelektrona jednaka nuli. Fotoelektroni su tek napustili metal, ali još nemaju dovoljno energije da se gibaju. Frekvencija pri kojoj je energija jednaka energiji vezanja je granična frekvencija:
$$h\nu _{0}=W_{0}\Rightarrow \nu _{0}=\frac{W_{0}}{h}$$
Jasno je da granična frekvencija ovisi o vrsti metala, jer energija vezanja ovisi o vrsti metala.
Ako je frekvencija upadnog zračenja manja od granične, fotoefekta nema, jer bi tada kinetička energija bila negativna.
Ako je frekvencija veća od granične, fotoefekt se opaža, a kinetička je energija linearna funkcija frekvencije, u skladu sa eksperimentom, kao što se vidi na grafikonu (a).
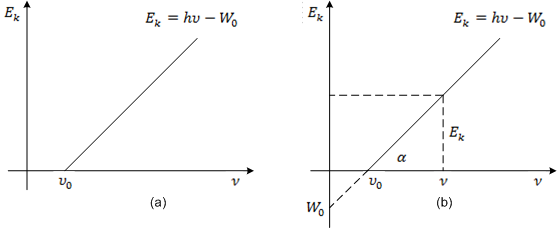
Graničnu frekvenciju za dani metal odredimo iz izlaznog rada, dok kinetičku energiju možemo odrediti pomoću napona električnog polja potrebnog za zausatvljanje fotoelektrona: Ek = eU.
Napomenimo da se u svim izrazima radi o najvećoj kinetičkoj energiji emitiranih fotoelektrona. Svi elektroni nemaju jednaku kinetičku energiju, pogotovo oni koji se nalaze u "dubini" atoma, jer na svom putu prema površini metala gube dio energije na sudare sa atomima.
Valna i čestična priroda svjetlosti
Valna teorija o prirodi svjetlosti postala je općeprihvaćena početkom 19. stoljeća. Niz eksperimenata sa interferencijom i difrakcijom svjetlosti uvjerio je fizičare da je ispravna valna, a ne čestična teorija o prirodi svjetlosti.
Einsteinovo objašnjenje fotoefekta ponovo je aktualiziralo čestičnu teoriju o prirodi svjetlosti, barem kada je u pitanju međudjelovanje svjetlosti sa elektronima. Da li je to onda značilo da treba odbaciti valnu teoriju o prirodi svjetlosti i vratiti se na čestičnu?
Ili je možda svojstvo same svjetlosti da se nekada ponaša kao val, a nekada kao čestica? Ako je tako, kako saznati kada dominiraju valna a kada čestična svojstva?
Ta su pitanja nastala u vezi sa pretpostavkom o čestičnoj prirodi zračenja. Na sličan se način postavljalo i pitanje o česticama: ako se svjetlost ponaša dvojako, nekada kao val a nekada kao čestica, da li se možda i elektron, za kojega se oduvijek mislilo da je čestica, ponekad ponaša i kao val?
Odgovore na ta pitanja dobili smo dvadesetih godina prošlog stoljeća u nizu eksperimenata u SAD i Velikoj Britaniji. Eksperimenti su pokazali da i svjetlost i elektroni mogu imati svojstva valova i svojstva čestica. Taj čestično-valni dualizam postao je osnovna činjenica teorije koja je tada nastala i koju nazivamo valna mehanika, odnosno kvantna mehanika. Prvi od spomenutih eksperimenata ukazao je na čestična svojstva zračenja (Comptonov o raspršenje), a drugi na valna svojstva elektrona (difrakcija elektrona na kristalima).
De Broglieva valna duljina
Einsteinovo objašnjenje fotoefekta i Comptonovi eksperimenti raspršenja fotona na elektronima pokazali su da elektromagnetsko zračenje ima svojstva koja se mogu usporediti sa svojstvima materijalnih čestica. Louis de Broglie je 1924. godine pretpostavio da se, osim čestičnog ponašanja valova, mora opaziti i valno ponašanje čestica.
Da bismo mogli opisati val, moramo poznavati njegovu valnu duljinu. Poznato je da foton, kao čestica, ima energiju i impuls:
$$E_{f}=h\nu =h\frac{c}{\lambda };\, p_{f}=\frac{E}{c}$$
Prema tome, impuls fotona je:
$$p_{f}=\frac{h}{\lambda }$$
De Broglie je pretpostavio da ista ova relacija mora vrijediti i za materijalne čestice koje se gibaju, tj. da svaka takva čestica ima valnu duljinu
$$\lambda =\frac{h}{p }$$
Budući da je impuls čestice jednak p = mv, valna se duljina može prikazati i kao:
$$\lambda =\frac{h}{mv }$$
Tri godine nakon ove pretpostavke, valna svojstva elektrona bila su i dokazana. To su napravili Davisson i Germer u USA i Thomson u Velikoj Britaniji.
Bohrov model atoma
Prema Rutherfordu, atom se sastoji od pozitivno nabijene jezgre, u kojoj je koncentrirana gotovo sva masa atoma i elektrona, koji se gibaju po kružnicama, kojima je jezgra središte. Ovaj je model nazvan i planetarnim modelom zbog sličnosti gibanja planeta oko Sunca.

Ovaj model nije mogao objasniti:
Stabilnost atoma
Zbog djelovanja električne sile, elektroni bi se gibali po sve manjim i manjim kružnicama i na kraju bi pali na jezgru. Atom bi prestao postojati.
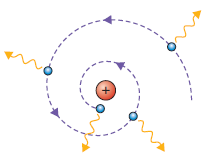
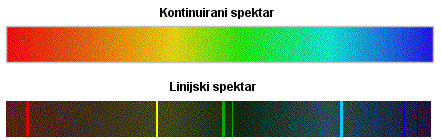
Izgled atomskih spektara
Pri takvom gibanju polumjer staze elektrona bi se kontinuirano smanjivao pa bi atomi zračili elektromagnetske valove svih valnih duljina unutar neke dvije valne duljine, pa bi spektri morali biti kontinuirani. Eksperiment je, međutim, pokazao da spektri nisu kontinuirani, linijski ili diskretni
Bohrovi postulati
Prema Bohru, elektroni se ne mogu gibati po bilo kojim kružnicama, nego samo po onima čiji polumjer zadovoljava relaciju:
$$mv_{n}r_{n}=n\frac{h}{2\pi }$$
- $m = 9.1\cdot 10^{-31}\,kg$ - masa elektrona
- $h=6.626\cdot 19^{-34}\,Js$ - Planckova konstanta
- $v_{n}$ - brzina elektrona u n-toj kružnici
- $r_{n}$ - polumjer n-te kružnice
- n = 1, 2, 3, 4, 5, ... - glavni kvantni broj
Polumjer prve dopuštene kružnice za vodikov atom je:
$$r_{1}=5.29\cdot 10^{-11}\,m$$
Polumjer bilo koje kružnice možemo prikazati kao:
$$r_{n}=r_{1}\cdot n^{2}$$
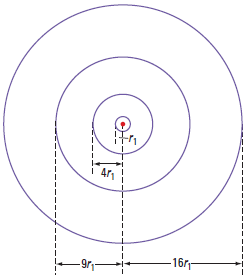
Dok se elektron giba po nekoj od tih kružnica, on ne zrači elektromagnetske valove, ne gubi energiju i, prema tome, nema razloga pasti na jezgru. Zato je atom stabilan.
Kada se elektron nalazi u prvoj dopuštenoj stazi, vodikov atom ima energiju:
$$E_{1}=-13.6\,eV$$
Općenito, ako se elektron nalazi u n-toj stazi, energija vodikova atoma je:
$$E_{n}=\frac {E_{1}}{n^2}$$
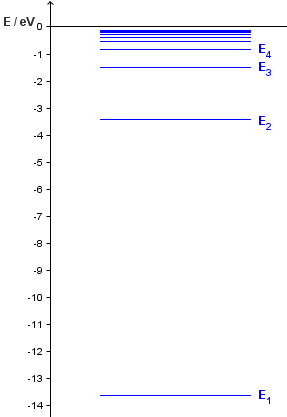
Na crtežu su prikazane energetske razine vodikova atoma.
Na crtežu možete primijetiti da se za velike n razine teško mogu razlučiti, jer se mijenjaju skoro kontinuirano.
Ako je atom prepušten samome sebi, on se nalazi u stanju najniže energije, E1. Ovo stanje nazivamo osnovnim stanjem. Sva ostala stanja su pobuđena stanja.
Da bismo atom prebacili iz osnovnog u pobuđeno stanje, ili iz nekog nižeg u neko više pobuđeno stanje, moramo mu dovesti energiju. To možemo učiniti na razne načine, na primjer, da ga "gađamo" fotonima nekog elektromagnetskog zračenja. Ako atom dobije dovoljno energije priječi će u neko više pobuđeno stanje. Ovo nazivamo apsorpcijom zračenja.
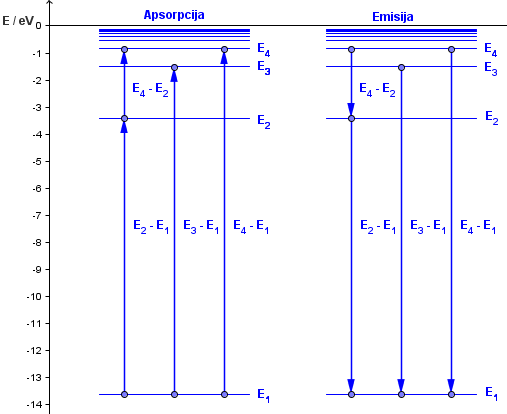
Enegija koju atom treba dobiti da bi prešao iz stanja niže energije, Em, u pobuđeno stanje veće energije, En, mora biti najmanje jednaka razlici tih energija, Emn = En - Em. Ako je energija manja, atom neće prijeći u stanje En, ako je jednaka, prijeći će u stanje En, a ako je veća, prijeći će ili u stanje En, ili u neko više, ovisno koliko je veliku energiju dobio.
U pobuđenom stanju atom će ostati jedno kratko vrijeme, a zatim će se spontano vraćati u niža energetska stanja, sve do osnovnog. Pri tim prijelazima dolazi do emisije elektromagnetskog zračenja. Ako je atom prešao iz stanja s energijom En u stanje s energijom Em, emitirani foton imat će energiju Ef = En - Em, pri čemu je n > m.
Frekvenciju emitiranog zračenja možemo odrediti iz:
$$h\nu =E_{n}-E_{m}\Rightarrow \nu =\frac{E_{n}-E_{m}}{h}$$
a valnu duljinu iz:
$$\frac{hc}{\lambda }=E_{n}-E_{m}\Rightarrow \lambda =\frac{hc}{E_{n}-E_{m}}$$
Spektar vodika je linijski spektar
Promotirmo valne duljine zračenja koje nastaje prijelazima atoma vodika iz stanja energije E3, E4, E5, ..., u stanje energije E2.
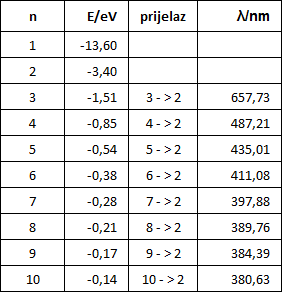
Vidimo da se u spektru pojavljuju samo neke linije. Zato takve spektre nazivamo linijskim. Izostanak drugih valnih duljina tumačimo time da jednostavno ne postoje energetska stanja među kojima bi prijelazi prouzrokovali emisiju elektromagnetskih valova nekih drugih valnih duljina.

Princip neodređenosti
U klasičnoj fizici nema ograničenja na točnost mjerenja, osim onih koja su uvjetovana točnosti instrumenata. Tako, na primjer, u svakom trenutku možemo izmjeriti položaj i brzinu, odnosno, količinu gibanja (impuls) neke čestice.
U kvantnoj mehanici, međutim, postoji principijelno ograničenje točnosti mjerenja. Nije moguće istodobno točno odrediti položaj i impuls kvantne čestice. Ovo je 1927. otkrio Werner Heisenberg a poznato je kao Heisenbergov princip neodređenosti. Ovaj princip najlakše možemo shvatiti ako krenemo od valnih svojstava čestica. Pretpostavimo da nekoj čestici točno poznajemo de Broglievuvalnu duljinu. To znači da je val prikazan beskonačnom sinusoidom.

Točno poznavanje valne duljine značit će, zbog p = h/λ, i točno poznavanje impulsa. Međutim, val se prostire duž cijele osi x pa znači da se čestica može nalaziti bilo gdje duž osi x, odnosno, njezin je položaj potpuno neodređen. Prema tome, točno poznavanje impulsa čestice ima za posljedicu potpuno nepoznavanje položaja čestice.
Uzmimo sada primjer kvantne čestice, poput fotona ili elektrona. Takve čestice predstavljamo valnim paketom i njihov je položaj lokaliziran.
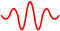
Ovdje valnu duljinu slabo poznajemo. Teško je uopće govoriti o valnoj duljini, kad znamo da je ovaj valni paket nastao superpozicijom puno valova različitih valnih duljina. Prema tome, vrlo loše poznajemo i impuls čestice. No, zato položaj poznajemo dobro, jer se radi o čestici, a čestice nisu raširene duž osi x, nego su lokalizirane.
Neka je Δx - neodređenost u poznavanju položaja čestice, a Δp - neodređenost u poznavanju količine gibanja čestice.
Iz tablice možemo vidjeti sljedeće:
- što točnije poznajemo impuls čestice, to lošije poznajemo njezin položaj
- što točnije poznajemo položaj čestice, to lošije poznajemo njezin impuls

Ovu vezu između neodređenosti u poznavanju položaja i impulsa čestica kvantitativno je izrazio W. Heisenberg: Umnožak neodređenosti u poznavanju položaja i impulsa čestice, po redu veličine, jednak je Planckovoj konstanti.
$$\Delta x\cdot \Delta p\approx h$$
Ovo je relacija neodređenosti, ili točnije, relacije neodređenosti, jer vrijede za sva tri smjera u prostoru.
Ovu relaciju često pišemo u sljedećem obliku:
$$\Delta x\cdot \Delta p_{x}\geq \hbar$$
Ovdje je:
$$\hbar=\frac{h}{2\pi }=1,05\cdot 10^{-34}Js$$
Rekli smo da se valni paket (foton) može dobiti superpozicijom valova različitih valnih duljina. To je razlog zašto valnu duljinu ne možemo točno odrediti. Valna je duljina povezana sa frekvencijom, c = ν·λ pa slijedi da ne poznajemo točno ni frekvenciju valnog paketa. Pretpostavimo da je ta neodređenost u poznavanju frekvencije jednaka jednom titraju: Δν = 1/Δt. Ovoj neodređenosti u frekvenciji odgovara neodređenost energije fotona:
$$\Delta E=h\Delta \nu \approx \frac{h}{\Delta t}$$
tako da dobijemo:
$$\Delta E\cdot \Delta t\approx h$$
Ovo je također Heisenbergov princip neodređenosti, prema kojemu ne možemo istodobno točno poznavati energiju čestice i vrijeme tijekom kojega čestica ima tu energiju. Ovo je ekvivalentno Heisenbergovim relacijama neodređenosti za položaj i impuls, a ima važno značenje, jer dopušta mogućnost narušavanja zakona očuvanja energije. Čestica može dobiti energiju veću za ΔE u tijeku vremena Δt, koje je određeno gornjom jednadžbom.
I ovu jednadžbu možemo i drugačije zapisati:
$$\Delta E\cdot \Delta t\geq \hbar$$
Kvantnomehanički model atoma
Budući da zbog relacija neodređenosti nikada ne možemo istodobno točno poznavati položaj i brzu elektrona u atomu, ne možemo govoriti niti o stazama elektrona. Pojam staze u kvantnoj fizici ne postoji. Možemo samo reći da se elektron nalazi negdje oko jezgre i da se giba u skladu s relacijama neodređenosti. Ne možemo točno reći gdje se u nekom trenutku nalazi. Jedino što možemo reći jeste kolika je vjerojatnost da se elektron nalazi na nekom mjestu. Zato govorimo o "elektronskom oblaku" ili oblaku vjerojatnosti. Gdje je "gustoća" toga oblaka veća, veća je i vjerojatnost da će se elektron tamo nalaziti. Najveća je vjerojatnost da će elektron biti na mjestu Bohrovih kružnica.