Rad

U prethodnom smo primjeru vidjeli kako rad iskazujemo energijom koja je zbog djelovanja dječaka, prešla s njega na kutiju. Kako odrediti rad?
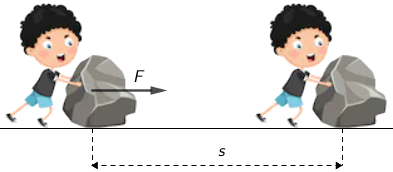
Dječak je na kutiju djelovao stalnom silom \(F\) duž puta \(s\). Sila i brzina imali su jednak smjer i orijentaciju.

Ako je smjer brzine tijela jednak smjeru sile koja na njega djeluje, rad definiramo kao umnožak sile i puta: \[W=F\cdot s.\]

Jedinica za rad džul (znak J) definirana je kao: \[\textrm{J}=\textrm{N}\cdot \textrm{m}.\]

Stalna sila djeluje u smjeru koji je različit od smjera gibanja

U ovom slučaju potrebno je odrediti komponentu sile u smjeru gibanja i pomnožiti ju s prijeđenim putom.

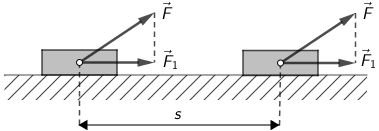
W = F1·s.
Ovako računamo rad uvijek kada je sila konstantna. Sila koja je okomita na smjer gibanja ne vrši rad (sila teža u ovome primjeru, ili centripetalna sila kod kružnog gibanja).

Rad promjenjive sile

Izraz za rad u ovom slučaju nije tako jednostavna i potrebno je znanje više matematike. Međutim, ako je poznat grafički prikaz sile duž puta, rad možemo odrediti grafički. U sljedećem je primjeru moguće odrediti rad i bez više matematike. Pokrenite simulaciju.

Osjenčana površina jednaka je izvršenom radu. Rad možete odrediti pomoću formule za površinu trapeza ili površinu podijeliti na pravokutnik i trokut pa primijeniti formule za njihovu površinu.

Pomicanjem bijelo obojenih točaka na osi s možete mijenjati put na kojem je djelovala sila, dok pomicanjem točaka na grafu sile mijenjate taj graf.

Primjer u kojemu je rad moguće odrediti višom matematikom, no u srednjoj se školi to ne radi. Rad se može približno odrediti tako da se na malim dijelovima puta pretpostavi da je sila konstantna, pa se računaju površine pravokutnika koje se na kraju zbroje. Točan rezultat može se dobiti pomoću sljedećg apleta. Osjenčana površina jednaka je radu. Pokrenite simulaciju.

Primjeri

Trenje između kutije i podloge je zanemareno pa se kutija se giba jednolikom brzinom.