Očuvanje količine gibanja

Sustav je zatvoren ako nema međudjelovanja sustava s okolinom. Očuvanje količine gibanja moguće je formulirati na sljedeći način:

Ukupna količina gibanja u zatvorenom sustavu je konstantna.

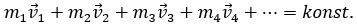
Teorijski izvod

Do zakona očuvanja količine gibanja moguće je doći primjenom trećeg Newtonovog zakona.

Impuls sile kojom je automobil A djelovao na automobil B jednak je: \[F_{\textrm{AB}}\Delta t=m_{\textrm{B}}v'_{\textrm{B}}-m_{\textrm{B}}v_{\textrm{B}}\] Impuls sile kojom je automobil B djelovao na automobil A jednak je: \[F_{\textrm{BA}}\Delta t=m_{\textrm{A}}v'_{\textrm{A}}-m_{\textrm{A}}v_{\textrm{A}}\] Prema trećem Newtonovom zakonu sile \(F_{\textrm{AB}}\) i \(F_{\textrm{BA}}\) djeluju duž istog pravca, a orijentacija im je suprotna: \[F_{\textrm{BA}}=-F_{\textrm{AB}}\] Pomnožimo ovu jednadžbu s Δt: \[F_{\textrm{BA}}\Delta t=-F_{\textrm{AB}}\Delta t\] Ako uzmemo u obzir prethodne dvije jednadžbe, dobijemo: \[m_{\textrm{A}}v'_{\textrm{A}}-m_{\textrm{A}}v_{\textrm{A}}=-m_{\textrm{B}}v'_{\textrm{B}}+m_{\textrm{B}}v_{\textrm{B}}\] Količine gibanja prije sudara prebacimo na lijevu stranu, a količine gibanja nakon sudara na desnu stranu: \[m_{\textrm{A}}v_{\textrm{A}}+m_{\textrm{B}}v_{\textrm{B}}=m_{\textrm{A}}v'_{\textrm{A}}+m_{\textrm{B}}v'_{\textrm{B}}\] Posljednji izraz prikazuje zakon očuvanja količine gibanja za dva tijela.