Elastična potencijalna energija

Elastična tijela (elastična opruga, gumena vrpca, lopta, itd.) nakon prestanka djelovanja vanjske sile vraćaju se u svoj prirodni oblik.

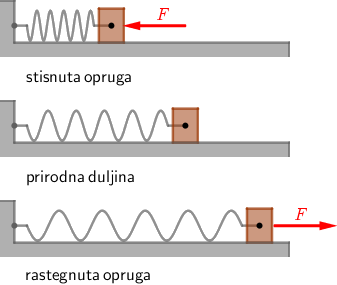
Elastičnu potencijalnu energiju definiramo kao rad koji izvrši vanjska sila pri istezanju ili stiskanju opruge.

Aplet

Pomoću klizača mijenjajte duljinu za koju stišćemo oprugu.

Pokrenite simulaciju.
O čemu ovisi elastična energija opruge?

Izraz za elastičnu potencijalnu energiju

Naučili smo da se rad može prikazati kao: \[W=F\cdot s\] No, to vrijedi samo ako je sila konstantna.
Elastična sila ovisi o deformaciji opruge: \[F=k\cdot x\] Zato moramo odrediti srednju silu. Ona je jednaka aritmetičkoj srednjoj vrijednosti početne i konačne sile jer sila linearno ovisi o deformaciji: \[\bar{F}=\frac{1}{2}kx\] Rad kojega je potrebno izvršiti da oprugu rastegnemo ili stisnemo za \(x\) jednak je elastičnoj potencijalnoj energiji opruge: \[W=\bar{F}\cdot x=\frac{1}{2}kx^{2}\] prema tome, elastičnu potencijalnu energiju možemo prikazati kao: \[E_{\textrm{el}}=\frac{1}{2}kx^{2}\]

Potencijalnu energiju moguće je pohraniti

Ako neki predmet želimo podignuti na određenu visnu jednolikom brzinom, moramo obaviti rad djelovanjem vanjske sile koja je po iznosu jednaka gravitacijskoj sili.
Želimo li stisnuti elastičnu oprugu također moramo obaviti rad djelovanjem vanjske sile koja je u svakom trenurku jednaka elastičnoj sili.
U oba primjera rad vanjske sile pretvorio se u potencijalnu energiju. Ti primjeri pokazuju da energiju možemo pohraniti za kasniju uporabu.