Induktivni otpor - sažetak
Ako na krajeve zavojnice priključimo izmjenični napon, koji se može prikazati jednadžbom $\color{Red} {U=\color{Red}U_0sin(\omega t)}$, zavojnicom će prolaziti izmjenična struja: $\color{Red} {I=\color{Red}I_0sin(\omega t-\pi/2)}$. $U_0$ i $I_0$ su maksimalne vrijednosti izmjeničnog napona i struje, dok je $\omega$ frekvencija izmjeničnog napona. Plavom sinusoidom prikazan je napon, a crvenom struja.
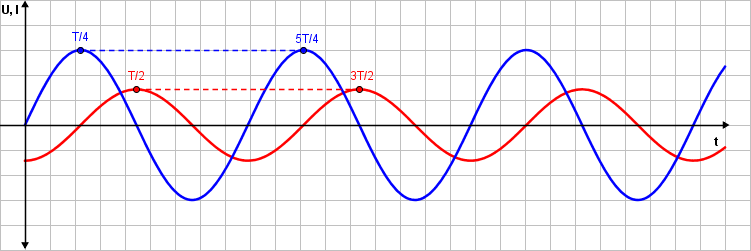
Iz ovih grafova zaključujemo da struja kasni za naponom za $t=T/4$, odnosno za četvrtinu perioda. To odgovara fazi: $$\color{Red} {\varphi =\omega t=\frac{2\pi }{T}\cdot \frac{T}{4}=\frac{\pi }{2}}$$ Kažemo da struja kasni u fazi za naponom za $\color{red}{\varphi=\pi/2\;rad \;}$.
Vidjeli smo također da je maksimalna vrijednost struje obrnuto razmjerna induktivitetu zavojnice i frekvenciji izmjeničnog napona:
$$\color{Red} {I_{0}\sim \frac{1}{L\omega }}$$
Iz Ohmovog zakona za istosmjernu struju znamo da je struja obrnuto razmjerna otporu, pa zaključujemo da je izraz $\color{Red} {L\omega }$ otpor. Budući da je taj otpor prouzrokovanom induktivitetom zavojnice, nazivamo ga induktivnim otporom i označavamo ga s $R_{L}.$
$$\color{Red} {R_{L}=L\omega }$$
Induktivni otpor posljedica je zaostajanja u fazi struje za naponom. To je otpor u smislu da prouzrokuje smanjenje jakosti struje kroz zavojnicu, međutim, na tom se otporu ne razvija toplina i ne troši se energija. Zato takav otpor nazivamo praznim otporom.
Da je ovako definirana veličina stvarno otpor, možemo se uvjeriti ako joj odredimo jedinicu:
$$\color{Red}{\textbf{[}R_L\textbf{]}=\textbf{[}L\textbf{]}\cdot \textbf{[}\omega \textbf{]}=H\cdot Hz=\frac{Vs}{A}\cdot \frac{1}{s}=\frac{V}{A}=\Omega}$$
Maksimalnu jakost struje koja prolazi krugom možemo odrediti iz Ohmovog zakona:
$$\color{Red} {I_{0}=\frac{U_{0}}{R_{L}}=\frac{U_{0}}{L\omega }}$$