Jednoliko uusporeno gibanje po pravcu - sažetak
To je gibanje po pravcu kod kojega je akceleracija konstantna, a vektori brzine i akceleracije imaju jednak smjer i i suprotnu orijentaciju.
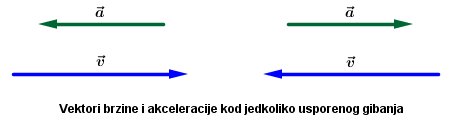
Akceleracija je definirana kao:
$$a=\frac{\Delta v}{\Delta t}=\frac{v-v_{0}}{t-t_{0}} \qquad \text {(1)}$$
U početnom trenutku t0 = 0 brzina je jednaka v0. Vektori akceleracije i brzine imaju suprotne orijentacije. Ako je brzina pozitivna, akceleracija je negativna i obrnuto. Ako brzini damo pozitivan predznak, akceleracija ima negativan, pa je brzina jednaka:
$$v=v_{0}-at \qquad \text {(2)}$$Iz prethodnog izraza vidimo da se brzina u jednakim vremenima smanjuje za jednake iznose.
Graf brzine u ovisnosti o vremenu (v - t graf) je pravac:
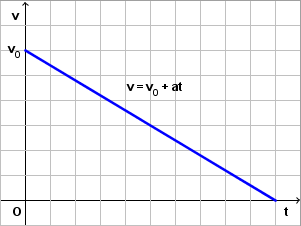
Iz ovog grafa možemo odrediti i pomak, odnosno prijeđeni put nakon nekog vremena kao pripadnu površinu:
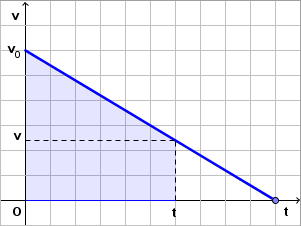
Ovu površinu možemo odraditi kao zbroj površina pravokutnika i trokuta, ili, jednostavnije, kao površinu trapeza. Ukupan put (ili pomak) nakon nekog vremena je:
$$s=\frac {v_0+v}{2}\cdot t \qquad \text {(3)}$$
Ako u ovu jednadžbu uvrstimo izraz za v iz jednadžbe (2), dobit ćemo:
$$s = v_{0}t-\frac {a}{2}t^2 \qquad \text {(4)}$$
Napravite to sami za vježbu!
Ako iz jednadžbe (2) izrazimo t i uvrstimo ga u jednadžbu (4), nakon kratkog računanja i sređivanja dobijemo:
$$v^2 = v_{0}^2-2as \qquad \text {(5)}$$
Napravite i to za vježbu!
Jednadžbe (2) do (5) korisno je znati jer nam pomažu pri rješavanju numeričkih zadataka.
Koliki je ukupni prijeđeni put za vrijeme zaustavljanja? Kolika je tada brzina?