Osnove molekularno-kinetičke teorije tvari

Osnovne činjenice molekularno-kinetičke teorije

Osnovne činjenice molekularno-kinetičke teorije su:

• molekule svih tijela se gibaju
• molekule svih tijela međusobno djeluju silama

Molekularno gibanje najjače je izraženo kod plinova, gdje je potpuno kaotično, dok je kod čvrstih tijela svedeno na titranje molekula oko ravnotežnog položaja. Molekularno gibanje kod tekućina je više izraženo nego kod čvrstih tijela a slabije nego kod plinova.

Molekularne sile najjače su kod čvrstih tijela, a najslabije kod plinova, dok su kod tekućina negdje između.

Toplinsko rastezanje tijela

Poznato je da se tijela zagrijavanjem šire, a hlađenjem stežu. Pri zagrijavanju molekule se gibaju većim brzinama pa se prostor između njih povećava - toplinsko širenje. Pri hlađenju, brzine molekula postaju manje, odnosno, udaljenost između njih je manja - toplinsko stezanje.

Linearno termičko širenje

Radi se o toplinskom rastezanju žice, štapa, ...

Označimo s $\ell_{0}$ duljinu tankog štap pri $0_{ }^{0}\textrm{C}$, a s $\ell$ duljinu pri temperaturi $t_{ }^{0}\textrm{C}$. Tada vrijedi:

$$\ell =\ell _{0}\left ( 1+\alpha t \right )$$

Koeficijent $\alpha$ nazivamo koeficijentom linearnog termičkog rastezanja a njegova vrijednost ovisi o vrsti materijala i može se naći u raznim tablicama ili može biti zadana u samom zadatku. Jedinica za ovaj koeficijent je $\left [ \alpha \right ]=K^{-1}$.

Ovaj izraz možemo primijeniti i na hlađenje tijela, samo treba uzeti u obzir da je tada temperatura negativna.

Model idealnoga plina

Sva su tijela građena od atoma, odnosno, molekula. Molekule se sastoje od jednog ili više atoma. U molekularno-kinetičkoj teoriji molekule možemo zamisliti kao malene kuglice promjera od $10^{-10} \,m$ do $10^{-9} \,m$

U modelu idealnog plina zanemarujemo sile između molekula.

1. molekularno gibanje je nasumično (nesređeno, kaotično)
2. sudari između molekula, te sudari molekula sa stijenkama posude u kojoj se plin nalazi su elastični
3. između dva uzastopna sudara molekule se gibaju kao slobodne čestice (djeluju silama samo u trenutku sudara)
4. gibanje molekula možemo opisati kao gibanje materijalne točke (srednja udaljenost između molekula puno je veća od promjera molekule)

Tlak plina

Tlak plina je posljedica molekularnog gibanja, odnosno, sudara molekula sa stijenkama posude u kojoj se plin nalazi. U tim sudarima molekule djeluju određenom silom, a sila po jedinici površine je tlak.

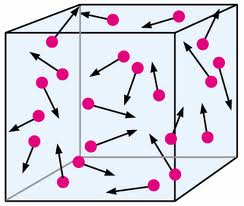
Polazeći od osnovnih postavki molekularno-kinetičke teorije, može se pokazati da je tlak plina jednak:

$$P=\frac{2}{3}\frac{N}{V}\overline{E}_{k}$$

N je broj molekula u posudi, V volumen posute, a $\overline{E}_{k}$ srednja klinetička energija molekularnog gibanja.

Brownovo gibanje

Brownovo gibanje dokazuje činjenicu da se molekule plinova i tekućina neprestano nasumično gibaju. Ako na površinu vode stavimo zrnca peluda i promatramo mikroskopom primjetit ćemo stalno gibanje čestica peluda. Slično se događa i sa česticama dima u zraku.

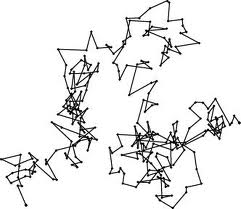
Brownovo gibanje tumačimo molekularno kinetičkom teorijom. Molekule tekućine ili plina gibaju se nasumično i udaraju čestice peluda, zbog čega se i one gibaju nasumično. Ovo se može opaziti samo kod čestica mikroskopske veličine (čestice kojima je promjer otprilike $10^{-7} \,m$ do $10^{-6} \,m$).

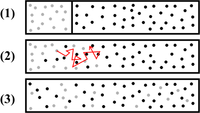
Difuzija

Prema Wikipediji, difuzija je miješanje tvari kroz njihovu dodirnu površinu ili propusnu membranu. Čestice (atomi, molekule, ioni, itd.) putuju iz područja više u područje niže koncentracije. Difuzija se najbrže odvija u plinovima, sporije u tekućinama a najsporije u čvrstim tijelima.

Srednja kinetička energija molekularnog gibanja i apsolutna temperatura

Difuzija je također dokaz molekularnog gibanja.

Srednja kinetička energija molekularnog gibanja ovisi o apsolutnoj temperaturi idealnoga plina i o broju atoma u molekuli:

$$\overline{E}_{k}=\frac{s}{2}kT$$

Konstanta s ima vrijednost:

• s = 3 za jednoatomne idealne plinove
• s = 5 za dvoatomne idealne plinove
• s = 6 za višeatomne idealne plinove

T je apsolutna temperatura (u K), a k je Boltzmannova konstanta:

$$k=1.38\cdot 10^{-23}\frac{J}{K}$$

Vidimo da je srednja kinetička energija molekula idealnoga plina proporcionalna apsolutnoj temperaturi. Ova nam jednadžba zapravo i služi za definiciju apsolutne temperature:

Apsolutna temperatura je veličina koja je proporcionalna srednjoj kinetičkoj energiji molekularnog gibanja.